基于直方图得分和模板更新得分的实时目标跟踪

2019-04-01肖春华

计算机应用与软件 2019年2期

李静肖春华

1(重庆工程学院科技处重庆 400056)2(重庆市数字影视与新媒体工程技术研究中心重庆 400056)3(重庆大学计算机学院重庆 400044)

0 引言

目标跟踪是机器视觉领域热门的基础性研究课题[1]。在安防、军事侦察、无人机等众多高新领域应用广泛。目前，目标跟踪的难点和挑战是如何较好地解决目标的形态变化、不准确预测造成的飘移现象、低分辨率的目标识别、多目标的遮挡和身份切换等问题[2-3]。

在已有的研究成果中，跟踪算法按照不同策略，可以分为基于学习的算法、基于滤波的算法和多跟踪器模式。基于学习的算法是一种自适应方法，即在线学习模式。如Struck[4]是一个性能较好、结构简单的在线目标检测与跟踪算法，该算法旨在将目标定位的结构化输出最小化，但较高的计算量限制了特征和训练样本的数量。文献[5]提出基于HOG在线多实例学习的目标跟踪算法，该算法采用HOG特征值提取方式，结合在线多实例学习技术，其适合于目标平移、旋转和遮挡等情况下的跟踪。

TLD(Tracking Learning Detection)算法[6]采用NP学习方法对训练出现的正负样本进行分类和纠错，通过修改训练策略提高预测的准确性，减少了目标漂移的可能性。文献[7]将协同训练应用到跟踪中，对两个独立的、使用了不同特征的支持向量机进行学习，随后从合并的分数中得出硬性否定。

基于滤波的跟踪大多会局限于对一个刚性模板的学习[8]。当目标发生形状变化时，跟踪会变得很困难，解决思路是采用一个对形状变化不敏感的表征形式，如KCF方法[9]。一般可以将直方图与相关滤波器正交，但仅靠直方图通常无法有效表征目标，为此，文献[10]对来自每个像素的投票进行累加，使用投票后得分最高的位置像素来估计目标的范围。但是，这类方法并不具有普遍适用性，假设条件较多。

对于一些特殊形式的运动方式，需要对跟踪形式进行改进。例如针对低秩假设的粒子滤波跟踪器难以跟踪突然运动目标的局限性，文献[11]提出时间受限的反向低秩视觉跟踪算法，利用反向低秩模型表示目标模板和背景模板，并利用混合范数进行局部约束，以保证目标外观的局部一致性，以及相邻帧之间的突然变化。

为了降低预测不准确性，一般可以结合多个估计手段，使跟踪器的弱点得到补偿。如文献[12]提出一种低复杂度交互式多模型滤波器，该跟踪算法组合了一些交互式滤波器，并且利用了整个滤波器组的卡尔曼滤波增益矩阵。文献[13]使用隐马尔科夫模型HMM(Hidden Markov Model)对目标轨迹以及不同时刻的跟踪器可靠性进行建模。但这类方法缺点是各跟踪器的复杂度和兼容性需要统筹考虑。

本文主要创新之处是所提跟踪器结合了两方面的得分：目标模板得分和直方图得分，建立线性组合模型。这两方面具备一些重要属性，即：得分在量值上具有相似性，可靠性较高，且目标的位置预测由置信度更高的一方所主导。这样使得跟踪器对互补性要素具有敏感性，对局部变化不敏感，所学习的模型对颜色变化和形变均具有一定的鲁棒性。另外，为保持实时的处理速度，本文还利用了每个图像块表示内在结构，并将其作为两个独立的岭回归框架[14]进行求解。实验结果验证了所提方法的优越性。

1 模型说明

本文目标跟踪采用了基于检测的跟踪范式，即：在帧t中，从集合St选出目标在图像xt中矩形跟踪框的位置得分pt：

pt=arg maxp∈Stf(T(xt,p);θt-1)

(1)

θt=arg minθ∈Q{L(θ;Xt)+λR(θ)}

(2)

式中：Q为参数θ的空间表示，本文使用正则化项R(θ)限制模型的复杂度，以防止过拟合。

式(1)中得分函数f(x)定义为模板(tmp)和直方图(hist)得分的一个线性组合：

f(x)=γtmp1ftmp1(x)+γhistfhist(x)

(3)

为了在滑动窗口的搜索中，高效计算得分函数，窗口图像特征共享重叠窗口，模板得分使用卷积快速计算，直方图得分通过单积分图计算获得。

在理想情况下，每帧图像训练损失函数的形式为：

(x,p,θ)=d(p,arg maxq∈Sf(T(x,q);θ))

(4)

式中:d(p,q)定义为：当正确矩形框为p时选择矩形框q的代价。虽然该函数是一个非凸性函数，但可使用结构化输出学习对目标的界限进行优化。然而，该优化的缺点在于计算成本很高，限制了可用特征和训练样本的数量。相比之下，相关滤波器采用了简单的最小二乘原理，可通过将特征图像的循环位移作为样本，使用较高维特征表示，从一个相对数量较大的训练样本中学习。该方法在跟踪中效果较好，同时保持了较高的运行速率。

因此，为了保持相关滤波器的速度和有效性，同时不忽略直方图得分所捕获到的信息，本文通过求解两个独立的岭回归问题学习所提模型，即：

(5)

式中:参数h可以使用相关性滤波公式快速得出。最后，选取两个模型得分的凸组合，设γtmp1=1-α，γhist=α，其中因子α是在验证集上选择的参数。以上两个模型得分函数的参数都将得到优化，目标的分数分配为1，其他窗口的分数分配为0。所提模型的总体示意图如图1所示。

图1 所提模型的总体示意图

2 优化与学习过程

2.1 在线最小二乘优化

本文采用最小二乘和二次正则算子有两个好处：1) 在闭合形式中得到解；2) 内存要求不会随样本数量的增加而增加。如果L(θ;X)是得分f(x;θ)的一个凸二次函数，而f(x;θ)在模型参数θ中是线性的(以保持凸性)，那么则会存在着一个矩阵At和一个向量bt，使得：

(6)

而无论Xt的大小如何，都足以确定解θt=(At+λt)-1bt。

如果采用一个递归定义的损失函数：

L(θ;X)=(1-η)L(θ;Xt-1)+η(xt,pt,θ)

(7)

式中:η为自适应率，则可维持：

(8)

(9)

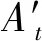
2.2 对模板得分进行学习

在最小二乘相关滤波中，每帧图像损失为：

(10)

(11)

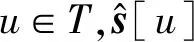
在实践中，本文没有对式(11)进行计算，而是采用了尺度估计的相关滤波器[15]进行近似。

模板在线更新表示为：

(12)

2.3 对直方图得分进行学习

理想情况下，直方图得分应该学习来自于每个图像的一个样本集合，其中包括作为一个正例的正确位置。设W表示矩形窗q和与之相对应的回归目标y∈的一个成对集合(q,y)，包括正例(p,1)。则每帧图像的损失为：

(13)

通过对一个M×M的方程组进行求解，得出M-通道特征变换ψ的解，求解该方程组的内存需求为O(M2)，时间需求为O(M3)。如果特征的数量较大，则上述方法不可行。虽然存在着其他的迭代方法对矩阵进行分解[10]，例如坐标下降法、共轭梯度和双坐标下降，但是仅靠这些方法依然难以实现较高的帧速率。

本文提出了形式的特征为ψ[u]=ek[u]，式中的向量e在下标为i时等于1，其他情况下则等于0。考虑的特征为量化的RGB颜色特征，直方图得分可被视为一个平均投票。因此，为了提高效率，本文建议将线性回归独立的应用到目标O和背景区域B∈2的每个特征像素，使用每帧图像目标:

(14)

式中:ψ为ψT(x,p)的简写。引入one-hot假设，目标分解为每特征维数独立项：

(15)

式中：Nj(A)=|{u∈A:k[u]=j|是∅T(x,p)的区域A中的像素数量，特征j为非零k[u]=j。则相关联的岭回归问题的解为：

(16)

对于每个特征维数j=1,2,…,M，其中ρj(A)=Nj(A)/|A|为一个区域中j为非零的像素比例。本文对模型参数进行更新:

(17)

式中:ρt(A)是ρjt(A)的向量，j=1,2,…,M。

3 实验与分析

本文在视频集VOT-14[2]和OTB-100[16]上对所提跟踪器和其他方法进行了比较，实验中所使用的重要参数如表1所示。

表1 本文实验中所采用的参数列表

3.1 VOT-14视频集

从VOT-14视频集的394个视频中选择25个序列，以代表相机运动、遮挡、光照变化、尺寸和运动，并在选出的序列上对跟踪器进行性能比较，该部分列举了有代表性8个视频的跟踪结果。比较的跟踪有文献[4]提出的Struck跟踪器，文献[5]提出的多实例学习的HOG跟踪方法，经典的TLD跟踪器[6]，以及改进的KCF跟踪器[9]。

使用的评价指标如下所示：

3) 跟踪器的鲁棒性为其在视频中失败的次数。当St变成零时，则判定出现了一次跟踪失败。由于该基准着眼于短时间跟踪，一个跟踪器在出现跟踪失败后，会在5帧之后被自动重新初始化到地面位置。

各跟踪器对各视频序列的平均每帧重叠结果如表2所示，平均重叠值越大，其对应的跟踪器越优，每一行的最优结果加粗显示。可以看出本文方法在大多数情况下，其重叠均达到最大。即使在次优情况下，也与最优相差不多。在地铁视频中表现不佳，可能是由于矩形包围框的中心位置造成的。不同跟踪器对包围柜中心误差的比较如表3所示。可以看出，本文方法的中心误差最低，跟踪的中心位置把握得更准确。25个视频的综合评价结果如表4所示。可以看出，本文方法的平均重叠更大，跟踪失败次数更少，综合评价得分最高。

表2 各跟踪器对视频序列的重叠值

表3 各跟踪器对视频序列的中心误差

表4 25个视频序列中的综合排名结果

为了研究形变对跟踪器的影响，选择一些形体不停发生变换的视频，如做复杂动作的运动员视频，如图2所示。其中第一行是多实例HOG方法的跟踪结果，第二行是改进KCF方法的跟踪结果，第三行是本文方法的结果。可以看出，本文方法在运动员的运动过程均得到了良好的跟踪。多实例HOG方法和KCF方法受到背景颜色的严重干扰，同时由于形变造成模板特征发生了较大变化，而本文方法充分利用目标模板和直方图得分的互补性对形变和背景具有较好鲁棒性。

图2 运动员视频中外观变化实验

为了研究光照变化对跟踪器的影响，选取了David视频中明暗变化的序列部分，该部分伴有较小形变过程，如图3所示。比较的方法与图2外观变化实验相同。可以看出多实例HOG和改进KCF方法由于更新误差积累导致了目标漂移，而本文方法对光照变化具有较好的鲁棒性。一般来说，基于相关滤波的跟踪器在应对运动、光照和尺度等变化时具有一定的鲁棒性，但局限于刚性模板的学习，当目标在一个视频序列中发生形变时，该类跟踪器会表现不佳。在所用特征中，颜色直方图会丢弃每个像素的位置信息，对形状变化具备鲁棒性，但不能很好地应对光照变化，且当颜色辨识度不高时通常无法有效地从背景中辨识。鉴于直方图和模板所具备的互补性，本文结合两个图像分块表示，对形状和颜色均具备鲁棒性。

图3 David视频序列中光照变化实验

3.2 OTB-100视频集

与VOT-14基准一样，OTB-100[16]的理念是在准确度和失败的鲁棒性两方面对跟踪器的性能进行评价，OTB-100视频集已经成为目标跟踪数据集的一个标准。准确度通过预测跟踪器的矩形包围框和实际情况的交集与并集之比进行度量。但用到了一个阈值to，当该比值高于阈值to时，则检测到一次成功的跟踪。为了不将该阈值设为一个特定数值，在成功率曲线下方处于不同数值的to区域作为一次最后得分，采用空间鲁棒性评价和时序鲁棒性评价评估跟踪器[16]。

本文使用了与VOT-14中相同的代码和参数进行测试，结果如图4和图5所示，可以看出，本文方法在成功率方面更优，总体上优于其他方法。其中，多实例学习的HOG整体比较差，鉴于该方法使用相关滤波器学习一个颜色模板，因此，本文方法的优越性表明，通过结合模板和直方图得分所实现的性能改善，不能单一地归功于对颜色的引入。

图4 时序鲁棒性评价

图5 空间鲁棒性评价

3.3 效率

本文采用MATLAB和C混合编程，在配置了Intel Core i5-4790K @8.0 GHz的台式计算机上以每秒大约80帧的速率运行。但是，通过对模型计算出的分块尺寸进行调节，可以牺牲较小的性能，以实现一个较高的帧速率。例如使用HOG的单元格尺寸为2×2，失败次数的增加较少，而速率则超过了每秒100帧。

3.4 学习率实验

本文分别将学习率ηtmp1和ηhist用于模板和直方图模型更新，以确定从之前帧中得到的旧证据替换为当前帧中得到的新证据。一般情况下，学习率越低，则从先前帧中学习到的模型实例相关性越高。实验结果表明，ηtmp1和ηhist均大约为0.01，可以达到最大程度的鲁棒性。

3.5 因子α的影响

本文方法的准确度(平均重叠值)受因子α的影响较大，其具体情形如图6所示，而式(3)中的γtmp1和γhist由α控制：在α=0.3附近，本文方法的性能最优。鲁棒性遵循类似的趋势。另外，图6还说明了对两个岭回归问题的密集响应进行合并的策略所达到的性能显著优于仅对最终估计进行插值的策略，即：具有相容且互补的密集响应模型能够获得较优的结果。