基于SA-AMG的弹塑性有限元计算的并行实现

张 倩 张健飞

(河海大学力学与材料学院 江苏 南京 211100)

0 引 言

当前，数值模拟理论已逐步完善并被广泛应用于科学、工程、生产等领域，而有限元法是其重要组成部分。弹塑性材料在实际中最为普遍，对其进行计算分析主要采用的就是弹塑性有限元法。与弹性有限元法相比，由于弹塑性有限元法的计算通常需要增量加载和迭代求解，因此其所需计算量和存储量要更多。随着工程规模的扩大和复杂性的增加，弹塑性有限元法对计算资源的要求越来越高，传统的串行算法已不再满足要求。随着超级计算机的持续开发，我国在硬件技术方面已经达到了世界先进水平，但在软件技术方面仍存在一定的问题。因此，为了扩大弹塑性有限元法的计算规模，充分利用超级计算机的计算能力，研究并开发了并行性和可扩展性均较高的弹塑性有限元并行程序。

有限元法的并行计算主要分为两种[1-2]：一是基于系统方程求解的方法，通常需要形成整体系统方程，且只能对求解部分并行化，所以存储量大、整体并行度不高；二是基于区域分解的方法，可以分为重叠型和非重叠型，无需形成整体系统方程，且各子区域独立计算，所以存储量小、整体并行度高。因此，有限元法的并行计算主要采用的是基于区域分解的方法。然而，从计算的角度来讲，有限元法的核心部分是求解方程组Ax=b，其并行求解器主要分为两类[3]：一是并行直接求解器，由于稀疏矩阵分解会导致非零填充，从而引起存储量和计算量的增加，且并行度有限，所以其只适合于求解中小规模问题；二是并行迭代求解器，由于避免了非零填充，所以其存储量和计算量小、并行度高。因此，对有限元法方程组的并行计算主要采用的是并行迭代求解器。

目前，弹塑性有限元法的并行计算[4-6]主要采用的求解方法是：先使用增量-牛顿法将非线性求解问题转换为迭代的线性求解问题，再使用预条件共轭梯度法对线性化后的方程组进行并行计算。其中，PCG的预条件可分为两种[7-10]：一是根据经典迭代法构造的预条件，如Jacobi预条件、多项式预条件等，其易于并行化，但迭代收敛的效果不理想；二是根据结合图着色的不完全分解形成的预条件，如ILU预条件、ICC预条件等，其属于直接法，故需要较大的存储量、计算量，且并行度较低。SA-AMG作为一种迭代法，其不仅易于并行化，而且具有很好的收敛性和可扩展性。

本文基于Trilinos软件包，利用增量-牛顿法、PCG和SA-AMG，实现了一种弹塑性问题的有限元并行求解方法，开发了相应的并行程序。通过对算例的计算，验证了算法和程序的正确性，分析了光滑聚集代数多重网格法不同的聚集策略、光滑算法和粗网格求解方法对计算性能的影响，测试了程序的并行性和可扩展性。

1 有限元法及其并行性分析

当利用有限元法对实际工程问题计算分析时，通常按照离散化、单元分析和整体分析的步骤进行，逐步形成单元层面的刚度矩阵Ke、等效结点荷载列阵Fe、结点位移列阵δe，以及整体层面的刚度矩阵K、等效结点荷载列阵F和结点位移列阵δ等。其中：离散化是将结构体划分成由有限个单元组成的网格模型，各单元间只通过相交的结点连接，并对其施加材料属性、荷载和边界条件等；单元分析是在每个单元中利用虚功原理或静力等效原则计算出其各自的Ke和Fe；整体分析是在每个结点处利用力的平衡条件将单元按照原始结构重新组合，由Ke和Fe分别累加得到K和F，从而形成有限元方程：

Kδ=F

(1)

对于弹塑性材料模型，由于其具有非线性的应力-应变关系，所以弹塑性有限元法的方程组是非线性的，即：

K(δ)δ=F

(2)

式中：K(δ)表示K中的所有元素均可用δ中的相应元素表示。

对式 (2) 的计算通常使用增量-牛顿法：首先，设置荷载增量，将所施加的总荷载分成几段，并对其循环；然后，在每个循环中，使用牛顿法迭代；最后，在每次迭代中，对线性方程组并行求解。因此，通过两层循环迭代，就将求解非线性方程组转化为了求解线性方程组。求解得到未知量δ后，根据弹塑性力学理论即可求出其应变ε和应力σ。

根据有限元法的基本原理，在单元分析中Ke和Fe的求解仅利用本单元信息，所以只要将同一个单元的信息存储在同一个进程中，其计算就能够完全并行；在整体分析中K和F的求解是将单元进行循环并按照结点编号的顺序分别累加的，相互之间不需要通信，因此通过合理安排循环顺序就可以提高其并行性。

2 光滑聚集代数多重网格预条件共轭梯度法

本文对增量-牛顿法每次循环迭代中线性化后的方程组使用光滑聚集代数多重网格预条件共轭梯度法并行求解。其中，PCG[11]能有效求解线性代数方程组，已被广泛应用于有限元法的计算中；SA-AMG[12-13]是由多重网格法衍生而来的，但其仅依靠代数信息即可构造多重网格基本组件，核心思想是：在粗细网格层上均求解代数方程组，并分别用于消除低频和高频误差。

2.1 预条件共轭梯度法

对于线性方程组Ax=b使用PCG求解时，按以下步骤进行：

1) 假设解x的初始值为x0，令其残差为r0=b-Ax0，精确求解Mh0=r0，令p0=h0；

2) 当k=1,2,…时，进行如下迭代：

(3)

精确求解Mhk+1=rk+1，接着进行如下迭代：

(4)

上述算法中，M为预条件矩阵，其通过光滑聚集代数多重网格法近似求解，从而形成了SA-AMG预条件共轭梯度法。

2.2 光滑聚集代数多重网格法

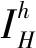
1) 细网格前光滑：

对Ahuh=fh做μ1次松弛迭代：uh←Sμ1uh+

2) 粗网格校正：

粗网格方程求解：AHuH=fH；

3) 细网格后光滑：

对Akuk=fk做μ2次松弛迭代：uh←Sμ2uh+

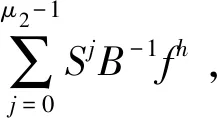
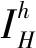
3 程序实现

本文程序主要基于Trilinos开发实现。Trilinos[16]是由Sandia实验室开发的大型数值软件包，其致力于更加便利地对数学软件库进行设计、开发、集成和支持， 目标是在面向对象的软件框架下开发解决大规模复杂物理工程和科学应用的并行算法和数学库。其中：ML库定义了一类基于多重网格法的预条件器；AztecOO求解器定义了一系列线性方程组的计算方法，包括预条件共轭梯度法；Epetra库定义了各种矩阵、向量和图表的构造和使用，支持串行、并行计算和分布式存储。

为了充分利用现有的串行弹塑性有限元程序资源，本文程序采用C++与FORTRAN混合编写。主程序利用C++编写，用于调用MPI、Metis以及Trilinos相关操作，实现增量-牛顿法对弹塑性有限元问题的循环迭代求解，其中方程组求解部分使用SA-AMG预条件共轭梯度法；子程序利用FORTRAN编写，用于执行与单元分析相关的计算。

在主程序中，首先读入有限元网格模型的相关信息，调用Metis将所有单元分解为几个子区域并分配给各个进程；然后各个进程分别调用弹性有限元FORTRAN子程序，计算弹性状态下的Ke并形成分布式存储的K；最后使用增量-牛顿法求解弹塑性有限元问题，进行荷载增量循环、牛顿法迭代：在每次迭代中，先计算Fe并形成分布式存储的F，调用Trilinos中的ML库和AztecOO求解器建立SA-AMG预条件共轭梯度法来并行计算；接着更新F并检验其是否收敛，如收敛则退出迭代，如不收敛则继续迭代，各个进程再分别调用弹塑性有限元FORTRAN子程序，计算弹塑性状态下的Ke并形成分布式存储的K和F。

3.1 整体刚度矩阵和整体等效结点荷载列阵的形成

在有限元法的单元分析中，其Ke和Fe的求解可以完全并行。利用Metis将所有单元分解成几个子区域并分配给各个进程后，一个子区域就对应一个进程，各个进程通过对其子区域中的单元进行循环，调用FORTRAN子程序，就可得到Ke、Fe和单元结点自由度列阵G。接着，根据G即可确定Ke和Fe中的元素分别在K和F中的位置，将其累加形成分布式存储的K和F。整体刚度矩阵K是按照Epetra库中的矩阵模式Epetra_FECrsMatrix来定义的，其采用了分布式稀疏行存储格式， 是一种专门针对有限元计算的矩阵存储格式。 整体等效结点荷载列阵F是按照Epetra库中的向量模式Epetra_Vector来定义的，其采用了分布式稠密存储格式。

3.2 求解方法的实现

在有限元法的整体分析中，分布式存储的K和F均求解完成后，便可形成线性方程组，通过调用Trilinos的ML库和AztecOO求解器对其进行并行计算。

求解部分程序的主要步骤为：首先，调用Epetra_LinearProblem定义每次迭代中线性化后的方程组Kx=F；然后，调用AztecOO求解器求解；接着，设置由ML库提供的光滑聚集代数多重网格预条件MLPrec的主要参数，如聚集策略、光滑算法和粗网格求解方法，并调用ML_Epetra::MultiLevelPreconditioner将参数组合；最后，将预条件MLPrec添加到AztecOO求解器中，形成SA-AMG预条件共轭梯度法，对线性化后的方程组进行并行计算，并设置AztecOO求解器的参数，如输出信息、最大迭代次数和收敛误差等。

4 数值实验

为检验算法和程序的正确性，分析光滑聚集代数多重网格法的主要参数对计算性能的影响，测试程序的并行性和可扩展性，在天河二号超级计算机上对程序进行了算例计算。

本算例采用如图1所示的厚壁圆筒三维结构，其内径10 mm，外径20 mm，长100 mm，两端各结点在X、Y、Z三方向均固定，其余结点在Z方向固定。内表面施加130 MPa的压力荷载，并将其划分为4个荷载增量。计算时均采用Von.Mises屈服准则，相关材料参数设置如下：屈服强度σY=380 MPa；弹性模量E=200 GPa；泊松比ν=0.3。利用Abaqus进行离散化，将厚壁圆筒结构划分成3种不同的有限元网格模型，即网格模型一：结点数32 340、单元数28 800、总自由度数62 040；网格模型二：结点数241 920、单元数228 000、总自由度数473 760；网格模型三：结点数1 889 280、单元数1 833 600、总自由度数3 739 202。

图1 算例示意图

4.1 算法和程序的验证

通过比较本文并行弹塑性有限元程序和既有串行弹塑性有限元程序在相同的网格模型下的计算结果，来验证算法和程序的正确性。采用网格模型一进行计算分析。根据力学基础知识可知，厚壁圆筒中段各点的位移应最大，所以从Z=50 mm的截面选取了如图2所示的代表结点，并分别提取了各点在X、Y方向上的位移UX、UY，如表1所示。

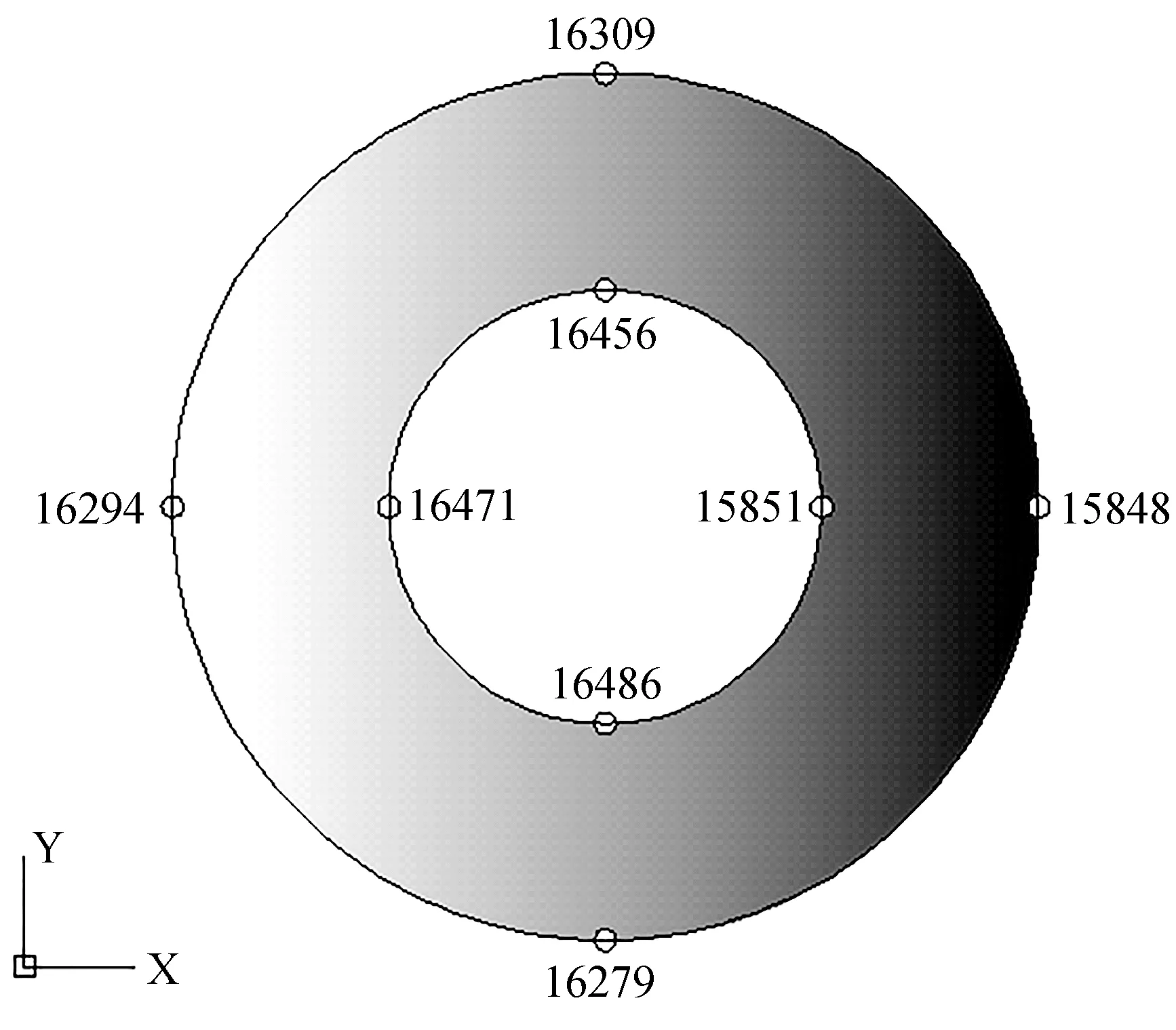
图2 Z=50 mm截面

mm

根据表1可以看出，本文并行弹塑性有限元程序和既有串行弹塑性有限元程序计算结果基本相同，因此算法和程序是正确的。

4.2 光滑聚集代数多重网格法的参数测试与分析

在利用Trilinos的ML库进行光滑聚集代数多重网格法计算时，其参数主要有3个：(1) 聚集策略，其控制粗化的过程，主要有MIS、Uncoupled和Uncoupled-MIS 3种类型；(2) 光滑算法，其控制光滑计算的过程，主要有Jacobi、Gauss-Seidel、Chebyshev和Aztec 4种类型；(3) 粗网格求解方法，其控制粗网格求解的过程，主要有Jacobi、Gauss-Seidel、Chebyshev和Amesos-KLU 4种类型。为分析以上各个参数对计算性能的影响，采用网格模型一进行测试分析，所需的求解时间变化如图3所示。由于光滑算法中Jacobi、Gauss-Seidel无论和谁组合，其收敛速度均较慢，在牛顿法迭代过程中，均未收敛，因此未包含在图3中。

图3 SA-AMG的不同参数组合对求解时间的影响

根据图3可以看出，3种聚集策略中所需求解时间最少的是Uncoupled-MIS；4种光滑算法中所需求解时间最少的是Aztec；4种粗网格求解方法中所需求解时间最少的是Amesos-KLU。因此，将3种参数组合计算效果最优的为Uncoupled-MIS+Aztec+Amesos-KLU。

4.3 程序并行性和可扩展性的测试与分析

本程序大致分为3大部分：首先，读入有限元网格模型的数据并利用Metis对所有单元进行分解，再将数据和分解结果广播到所有进程上；然后，分别计算各单元弹性状态下的Ke，并累加形成初始K；最后，在所有进程上进行增量-牛顿法的并行求解。为测试程序的并行性和可扩展性，分别对3种不同的有限元网格模型进行了不同进程数的并行计算，其中SA-AMG的主要参数采用了最优组合Uncoupled-MIS+Aztec+Amesos-KLU。统计了数据读入和区域划分时间、增量-牛顿法迭代求解时间和总运行时间，如表2-表4所示。根据表2-表4中的数据，又分别计算并绘制了增量-牛顿法迭代求解和总运行的并行加速比与进程数的关系，如图4-图6所示。

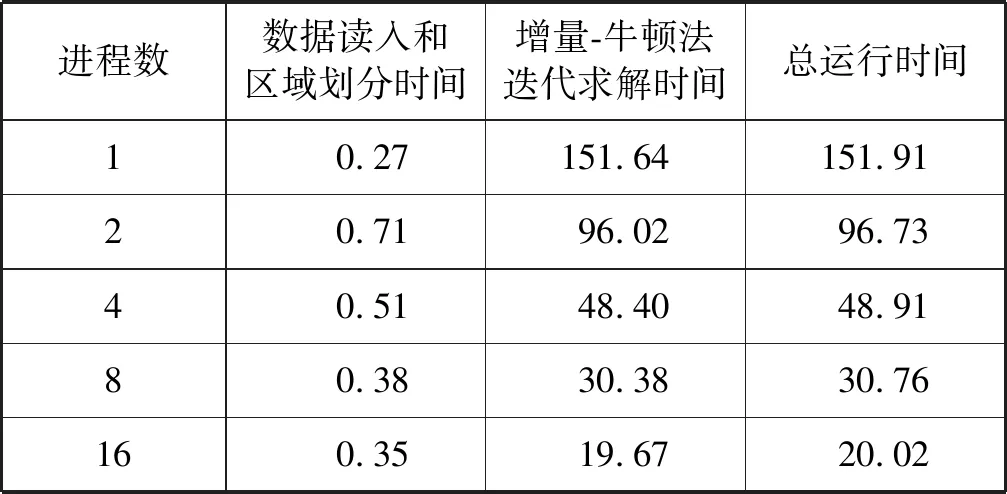
表2 网格模型一计算时间 s

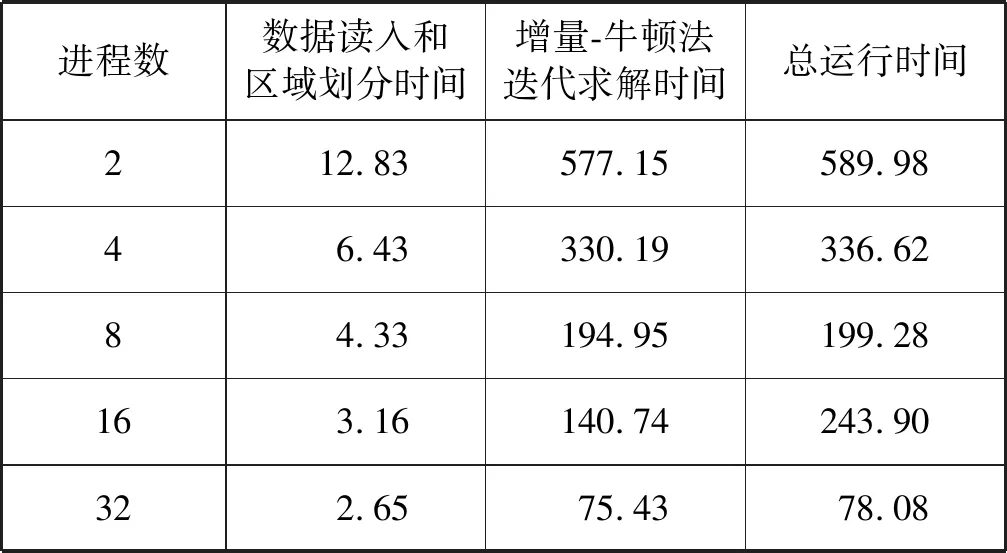
表3 网格模型二计算时间 s

表4 网格模型三计算时间 s

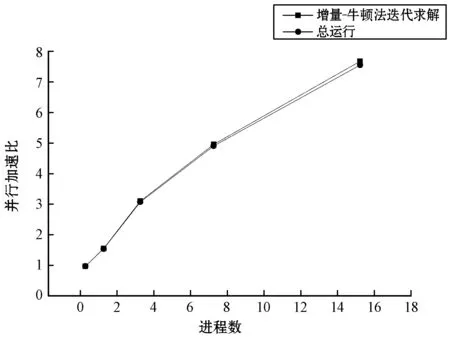
图4 网格模型一并行加速比与进程数的关系

图5 网格模型二并行加速比与进程数的关系

图6 网格模型三并行加速比与进程数的关系

根据表2-表4可以看出，数据读入和区域划分时间占总时间比例很小。对于相同的网格模型，随着进程数的增加，其稍有减少，这是因为进程间的数据通信量减少了。但对于相同的进程数，随着网格模型的扩大，其显著增多，这是因为区域分解复杂度、数据读入量和进程间的数据通信量都增加了。增量-牛顿法循环求解时间占总运行时间的绝大部分。对于相同的进程数，随着网格规模的扩大，其显著增多，这是因为计算量和数据通信量都有所增加。但对于相同的网格模型，随着进程数的增加，其显著减少，呈明显下降趋势，加速效果显著。

根据图4-图6可以看出，对于相同的网格模型，随着进程数的增加，其运行时间逐渐减少，但并行加速比并不呈线性，并行性能有所下降。这是因为每个进程中的计算量虽然减少了，但其子区域间的共享信息增加了，故进程间的数据通信量增加了，从而导致通信开销变多，致使并行性能逐渐变差。因此，对于特定的问题，计算时应充分考虑多方面因素的影响，从而选择最优的进程数和节点数进行计算，以充分发挥程序的并行性能。对于相同的进程数，随着网格模型的扩大，其运行时间虽有所增加，但其增加速度远小于网格模型的增大速度，因此，程序具有较好的可扩展性。

5 结 语

本文基于Trilinos的ML库和AztecOO求解器实现了一种弹塑性问题的有限元并行求解方法和程序，使用增量-牛顿法循环迭代求解非线性问题，其中SA-AMG预条件共轭梯度法为线性求解器。通过与既有串行弹塑性有限元程序计算结果的对比，验证了算法和程序是正确的；通过分析不同的光滑聚集代数多重网格法的主要参数对计算性能的影响，得到了计算效果最佳的组合为Uncoupled-MIS+Aztec+Amesos-KLU；通过测试不同的有限元网格模型的并行计算，证明了程序具有较好的并行性和可扩展性，可应用于大规模实际问题。