粘性Cahn-Hilliard方程解的渐近性

曹伯芳，姜金平，曹兰兰

(延安大学数学与计算机科学学院，陕西延安716000)

本文考虑以下粘性Cahn-Hilliard 方程：

ut+vΔ2u-δΔut=Δf(u)+g(x,t),

(x,t)∈Ω×(τ,∞)，

(1.1)

u=Δu=0,∂Ω×(τ,∞)，

(1.2)

u(τ,x)=uτ(x)，t>τ。

(1.3)

这里v>0，Ω⊂R2是具有光滑边界的有界区域,g(x,t)是关于时间t的外力项。δ>0是粘性系数，当δ=0时方程(1.1)就是我们熟知的Cahn-Hilliard方程，关于该方程已有很多作者进行了研究[1-5]。非线性项f满足以下条件：

f′(u)>-k,F(u)>μ，

(1.4)

存在正常数β,γ,k1,k2，其中0<γ≤β≤，

|f′(u)|≤k1(1+|u|β),

|f′(u)|≤k2(1+|u|γ)。

(1.5)

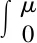
Cahn-Hilliard方程最早是由J.W.Cahn和J.E.Hilliard[6，7]提出，用以描述热力学中的两种物质相互扩散现象。文献[8-10]研究了方程解的存在性。在文献[8]中，Dlotko T.证明了当p≤2时Cahn-Hilliard方程在空间H1-H2中全局吸引子的存在性。文献[9]中，作者获得了Cahn-Hilliard方程关于强解的全局吸引子。董超雨[10]研究了Cahn-Hilliard的一致吸引子。王艳等[11]讨论了有界域上自治的Cahn-Hilliard方程指数吸引子的存在性。

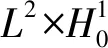
本文我们考虑利用一种新的方法，即通过压缩函数得到过程的渐近紧性，进而证明粘性Cahn-Hilliard一致吸引子的存在性。

1 预备知识

Lp(1≤p≤)是通常的勒贝格空间，Hs(Ω)是Sobolev空间。记H,V分别是拓扑空间(L2(Ω))2,(H1(Ω))2的闭包，(·,·)和‖·‖分别表示H中的内积和范数。

‖u‖2=(u,u),∀u,v∈(L2(Ω))2。

((·,·))和‖·‖V分别表示空间V中的内积和范数：

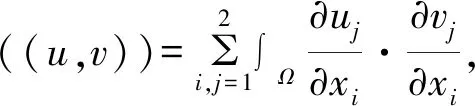
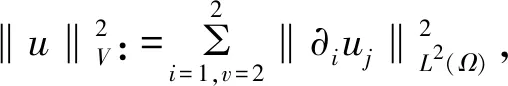
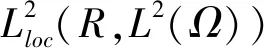
设X为Banach空间，∑ 是一个参数集，如果对每个f∈∑，{Uf(t,τ)}都是一个过程，即由X到X的双参数映射{Uf(t,τ)}满足：

Uf(t,τ)uτ=u(t,τ,uτ)，

(2.1)

Uf(t,s)°Uf(s,τ)=Uf(t,τ),

∀t≥s≥τ,τ∈R，

(2.2)

Uf(τ,τ)=Id,∀τ∈R。

(2.3)

其中：Id为恒等算子；∑为符号空间；f∈∑为符号。则称{Uf(t,τ)},f∈∑是Banach空间X的过程族。

设{T(s)}s≥0是作用在符号空间∑上的一族算子，满足

T(s)∑=∑,∀s≥0，

(2.4)

及平移恒等式：

Uf(t+s,τ+s)=UT(s)f(t,τ),

∀f∈∑,t≥τ,τ∈R,s≥0。

(2.5)

定义1.1 如果对任意的τ∈R和B∈B(E)，存在t0=t0(τ,B)≥τ，使得

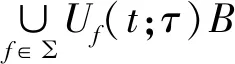
(2.6)

则集合B0∈E称为过程族{Uf(t,τ)},f∈∑的一致有界吸收集。

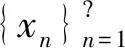
则我们把φ(·,·;·,·)称为定义在(X×X)×(∑×∑) 到B×B上的一个压缩函数。

记B×B上所有压缩函数的集合为Contr(B,∑)。

引理1.1 设{Uf(t,τ)},f∈∑是Banach空间X上的过程族，满足平移性(2.4) 和 (2.5)，并且{Uf(t,τ)}有一致有界吸收集B0⊂X，假设对任意的ε>0，存在T=T(B0,ε)和φT∈Contr(B0,∑)使得

‖Uf1(T,0)x-Uf2(T,0)y‖≤

ε+φT(x,y;f1,f2)，

∀x,y∈B0,∀f1,f2∈∑。

(2.7)

则{Uf(t,τ)},f∈∑在X上是一致渐近紧的。

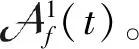
2 主要结果

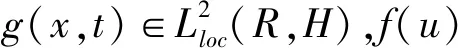
u∈C([τ,,H])∩L2(τ,T;V)。

证明定理的证明可通过Faedo-Galerkin方法得到，参照文献[18,19]。

引理2.1 设外力f∈∑,uτ∈H，则存在过程族{Uf(t,τ)}的一致有界吸收集B0。

证明对(1.1)式用u做内积，得到

(Δf(u),u)+(g(x,t),u)≤

(3.1)

(3.2)

那么

(3.3)

存在一个常数C1,使得

设C6=min{C4,C5}，有

(3.4)

对上式使用Gronwall引理可以得到我们的引理2.1。

引理2.2 假设f∈L2(R,H)，由问题(1.1)—(1.5)的全局解生成的过程{Uf(t,τ,uτ)}在H中是一致渐近紧的。

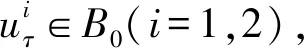
(3.5)

记w(t)=u1(t)-u2(t),那么w(t)满足以下方程

(3.6)

设

(3.7)

用w乘以(3.6)式并在[s,T]×Ω上积分，得

(3.8)

其中τ≤s≤T。则

(3.9)

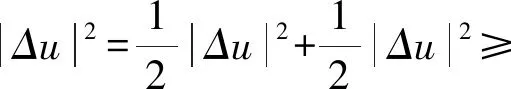
因此

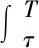
g2(h))w(h)dxdh)。

(3.10)

对(3.8)式在[τ,T]上关于s积分，得

g2(h))w(h)dxdhds。

令C0=CEw(τ)，

g2(h))w(h)dxdhds,

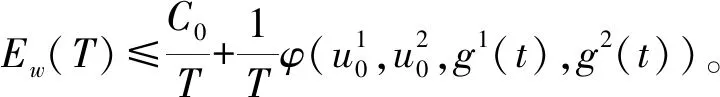
由于过程族有一个一致吸收集，我们选择T足够大使得

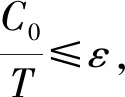
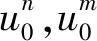
gm(t)∈∑,m,n=1,2…。由定理2.1，我们推出

um(s))dxds=0,

um(s))dxds=0,

um(s))dxdhds=0,

um(s))dxdhds=0。

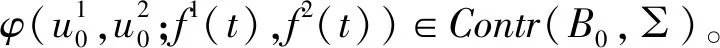
定理1.1的证明由定理2.1及引理2.1—2.2，利用文献[20]中经典的无穷维动力系统，可以直接得出结论。