超大型集装箱船载荷响应特性的数值研究

彭亚康，王伟飞，韩 钰，邱伟强，张志康

(中国船舶及海洋工程设计研究院，上海 200011)

0 引 言

近年来，集装箱船作为现代主流运输船承担着美国、英国、日本等国约70%~90%进出口的杂货。集装箱船在运输货物过程中体现了自身无与伦比的优势，集装箱船的装卸效率高、运输过程中货物损耗小以及能够大大节约装卸劳动力，因此集装箱船得到快速发展。随着二战后的经济快速发展，进出口货物与日俱增，短短半个世纪，从20世纪60年代的700-1000TEU快速发展到现在的万箱级别的超大型集装箱船，集装箱船尺寸也是越建越大。由于集装箱船尺度越来越大以及航速较高，在航行中会遇到一些问题，2007年1月18日，巴拿马级集箱船MSC Napoli在英吉利海峡遭遇风暴造成机舱壁处断裂，面临沉没的危险，26名船员被迫弃船；2013年6月17日，商船三井8110TEU型集装箱船“MOL Comfort” 号在也门外海200海里处遭遇恶劣天气导致货舱进水，使船从中部断裂。MAIB[1]与NK[2]的报告中显示弹性体效应造成的船底板强度不足是造成这2次事故的一个重大促成因素。

为更合理对超大型集装箱船进行结构设计，国内外很多学者根据弹性体的势流理论对超大型集装箱船进行波浪载荷计算。Senjanovic[3]等采用水弹性方法分析了1艘大型集装箱船的波浪载荷，并与基于刚体假设下的运动、波浪弯矩计算结果进行对比，发现对于大型集装箱船这一大开口船型，船体弹性效应十分明显。

李辉[4]发展了一套基于水弹性理论的波浪载荷计算方法，主要利用迁移矩阵法进行模态分析得出船舶的干模态的固有频率和固有振型，以干模态的固有振型作为广义坐标，再利用弹性体的势流理论计算水动力系数，并通过求解水弹性统一方程求得运动模态，最后通过物理关系并基于模态叠加原理求得剖面载荷等，此方法十分适用于散货船、油船等常规船型的载荷计算。由于没有考虑到船体的弯扭耦合效应，因而此套方法无法准确的用于集装箱船的波浪载荷计算。因而王迪[5]在此基础之上把船体简化为薄壁梁，根据薄壁结构力学相关理论采用迁移矩阵法计算了垂向和弯扭耦合模态其计算所得弯扭耦合模态达到了足够的精度。

Malenica 等[6 – 8]在利用频域格林函数法计算水动力的基础上，结合有限元模态分析结果计算了集装箱船所受波浪载荷，并且最终发布了集装箱船的波浪载荷计算商业软件Homer，取得很大成功。

国内外虽然有很多文献都研究过集装箱船的波浪载荷特性，但考虑到超大型集装箱船的弯扭耦合效应远远比小型集装箱船要明显，因而造成对于超大型集装箱船船体弯扭耦合模态对其所受波浪载荷数值结果的影响程度还不完全了解。为了分析超大型集装箱船船体弹性效应，特别是弯扭耦合效应对其所受波浪载荷数值结果的影响，本文首先分别采用有限元法和迁移矩阵法计算了目标船的干固有模态，为了说明问题，本文在利用有限元法计算模态时考虑弯扭耦合效应，而在用迁移矩阵法计算模态时不考虑弯扭耦合效应；在模态计算结果的基础之上采用三维水弹性理论计算目标船的波浪载荷，分析了目标船所受的波浪载荷特性以及通过对比展示了弯扭耦合模态对超大型集装箱船所受波浪载荷的影响程度。

1 理论基础

弹性船体在流场的振荡问题可以看成复杂的多自由度系统的振荡问题，则问题随时间t变化的微分方程如下式：

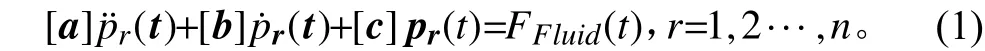
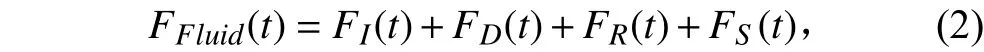
求得右端广义流体力后，可得到水弹性统一方程，见表达如下式：

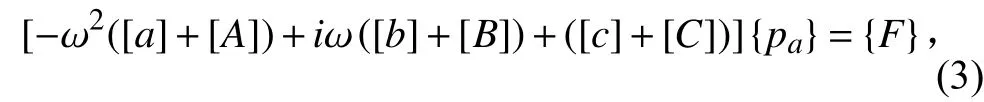
对频域方程组（3）进行求解后可得到船体运动和船体结构变形的主坐标，最后在模态分析的基础上利用模态叠加原理得到船体结构的位移和船体结构的剖面载荷，包括剖面弯矩和剪力。

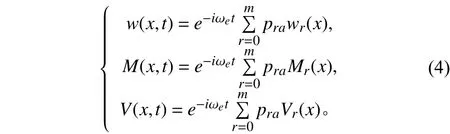
在波浪载荷计算过程中，广义质量矩阵、广义结构刚度矩阵以及广义结构阻尼矩阵可在模态分析时就得到确定，其中广义结构阻尼作为模态分析的一个输入一般由经验公式确定，广义流体载荷可由弹性体的三维势流理论计算而得，最后对水弹性统一方程组进行求解得到船体运动与结构变形的主坐标，继而通过结构变形与剖面载荷的物理关系求取剖面载荷，最后通过模态叠加法计算得到载荷。

2 模态分析

在基于水弹性理论计算波浪载荷时首先需对船体进行模态分析并获得船舶的振动干模态，以便把干模态的固有振型作为广义坐标对目标船进行载荷计算，模型主尺度见表1。

本节分别利用Femap，NX Nastran对有限元模型进行干模态分析以及利用迁移矩阵法对不考虑弯扭耦合效应的梁模型进行干模态分析。有限元模态计算结果如图1所示，不考虑弯扭耦合效应的迁移矩阵法计算结果如图2所示，固有频率计算结果见表2。

表 1 目标船主要参数Tab. 1 Main parameters of target ship

对比垂向弯曲模态结果可知，2种方法的误差不超过2%，从而可得出结论在计算扭转刚度较强、无甲板大开口的常规船型的垂向模态时，可利用迁移矩阵法大大简化计算。

迁移矩阵法计算结果中的纯扭转模态对应的固有频率十分低，这从侧面体现出超大型集装箱船扭转刚度弱的事实。通常海浪谱峰周期在10 s左右，即0.1 Hz，而扭转模态的固有频率比波浪频率还小，这会使得在计算剖面扭矩时，由于湿固有频率会十分接近波浪频率，会造成扭矩急剧增大的现象。

3 载荷响应特性研究

有限元法考虑了弯扭耦合效应，更加的符合集装箱船的变形特点，本节基于三维水弹性理论计算超大型集装箱船的载荷响应特性。计算水动力网格如图3所示，计算输入参数如表3所示。

针对表3需要说明的是，根据法国BV船级社推荐：计算弹振响应时，一个波长内至少有6个水动力网格，否则计算所得高频响应会不真实。因而考虑到13.5 kn航速和最大网格尺度为1.5 m的输入条件，波浪计算频率上限取为1.8 rad/s。180°浪向对应顶浪航行。

图 1 振动模态的有限元分析结果Fig. 1 Vibration mode results from finite element analysis

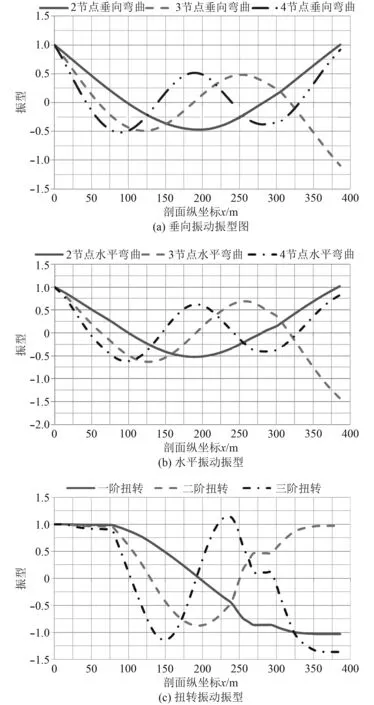
图 2 振动模态的迁移矩阵法分析结果Fig. 2 Vibration mode results from Transfer matrix method

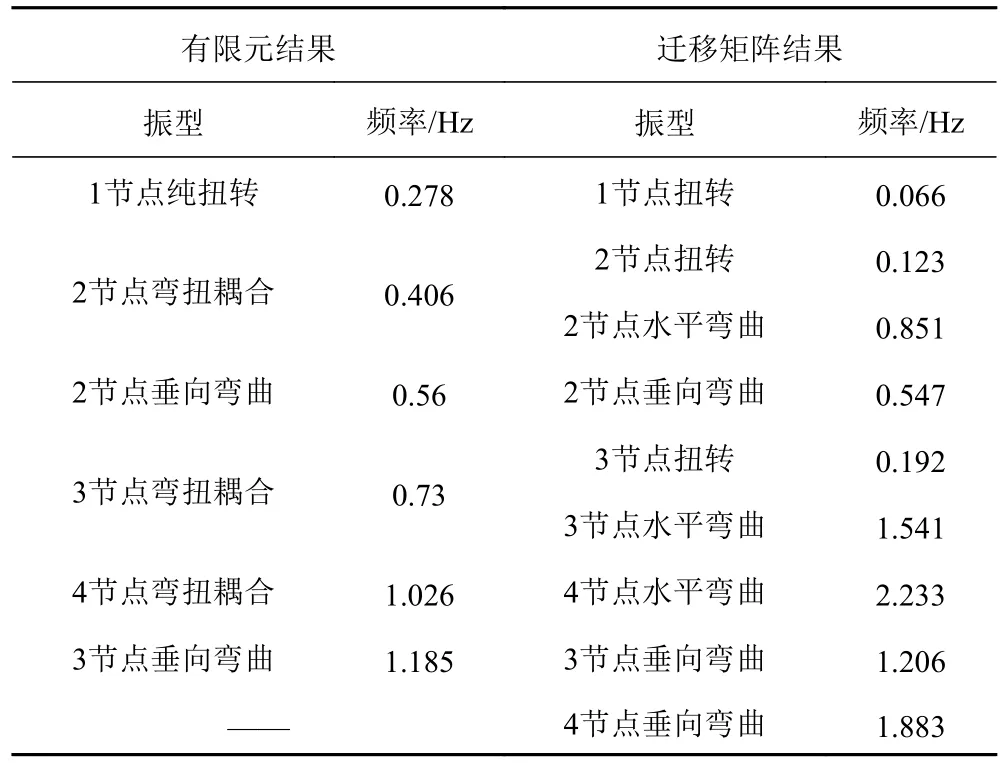
表 2 模态计算结果对比分析Tab. 2 Mode results from FE analysis

表 3 波浪载荷计算参数Tab. 3 Input parameters of wave loads calculation

波浪载荷计算结果如图4～图6所示，其中横坐标是遭遇频率所对应下的自然频率，Lbp指垂线间长，Rigid表示基于“船体假设为刚体”下的计算结果，Total表示为基于“船体作为弹性体”下的计算结果，Elastic-Contribution表示弹性效应的贡献。

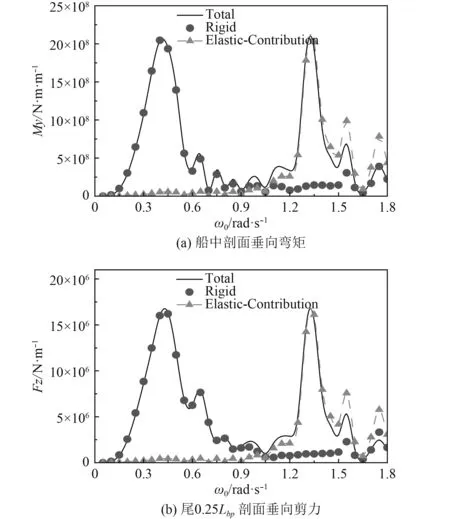
图 4 垂向载荷数值计算结果Fig. 4 Numerical results of vertical wave loads

从图中可以直观地看出，超大型集装箱所受垂向波浪载荷、水平波浪载荷在高频时很剧烈且和低频响应峰值在一个水平上，垂向弯矩和垂向剪力的规律一致，水平弯矩和水平剪力的规律一致，把图中高频响应峰值点所对应的自然频率换算成遭遇频率并和表2对比，可知垂向载荷、水平载荷的高频响应峰值点所对应的遭遇频率分别和2节点垂向模态、2节点弯扭模态对应的湿固有频率完全对应。

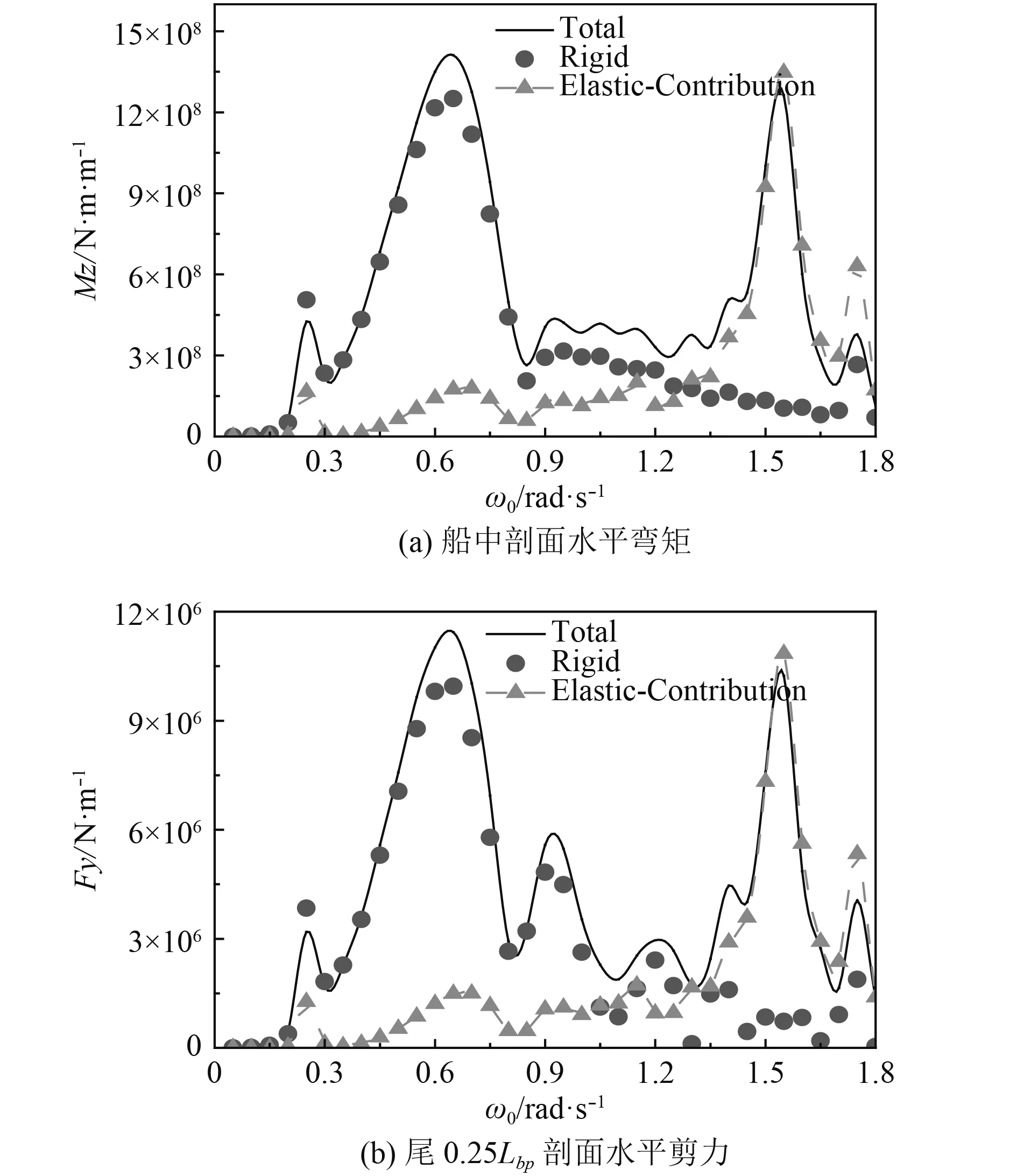
图 5 水平载荷数值计算结果Fig. 5 Numerical results of horizontal wave loads

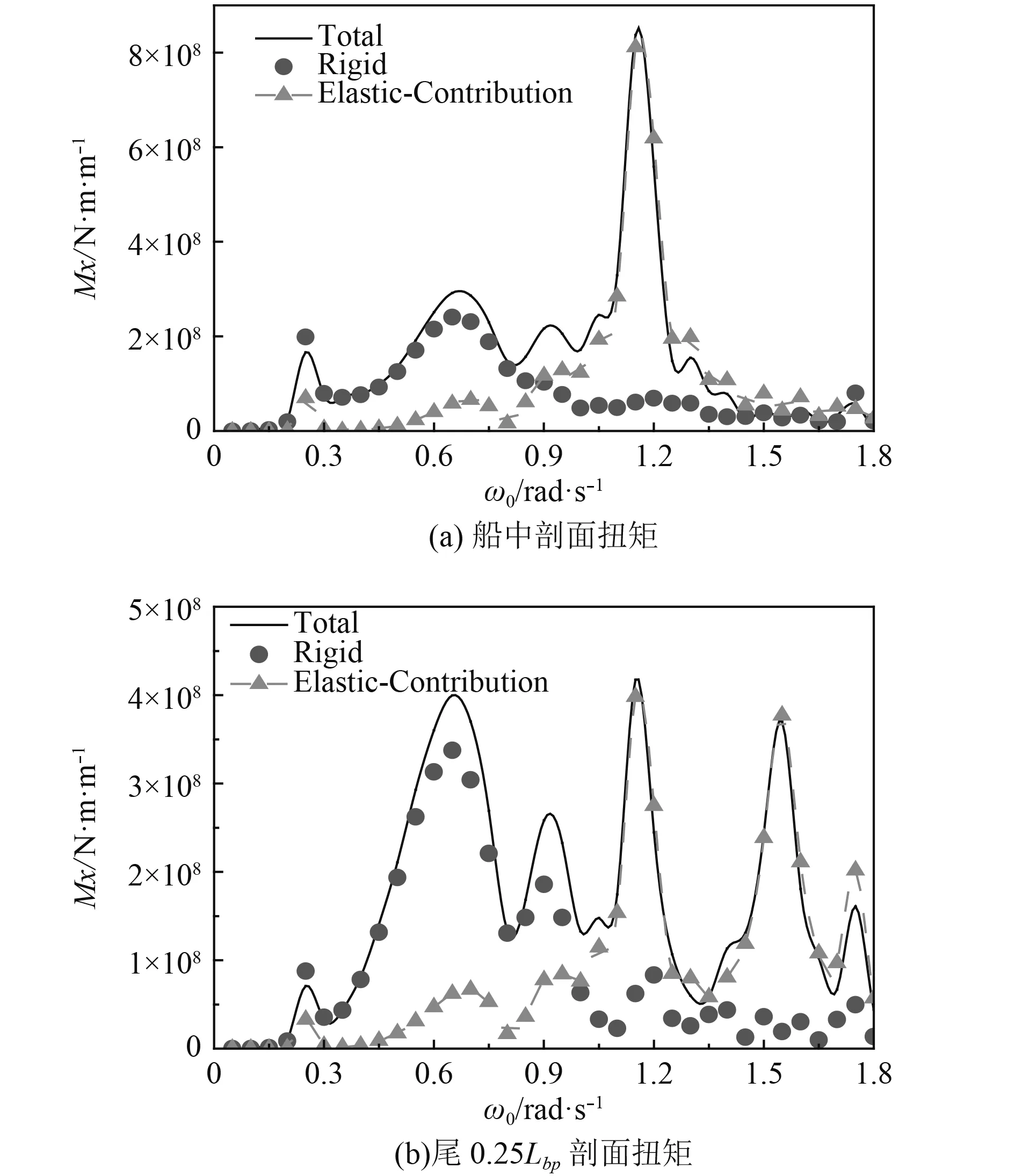
图 6 扭矩的数值计算结果Fig. 6 Numerical results of torque

在首120°斜浪航行下，船中剖面所受扭矩的高频响应远远大于低频响应；尾0.25 Lbp剖面扭矩产生了3个和低频响应处于同一水平大小的峰值。根据峰值点所对应的频率可知，剖面所受扭矩与模态相关，船中剖面主要受1节点扭转模态的影响，而尾0.25 Lbp剖面扭矩主要受1节点扭转和2节点弯扭模态影响。

从以上结果可以看出，超大型集装箱船的弹性体效应十分明显，航行过程中产生的高频响应不可忽视，并且此高频响应的峰值点对应的频率很低，在实际海浪谱峰周期附近，很容易在波浪的激励下产生高频响应从而危及到船体的使用寿命。

4 弯扭耦合效应对超大型集装箱船的影响研究

鉴于相对于其他船型，超大型集装箱船具有明显的弯扭耦合现象，因而本节研究船体的弯扭耦合模态对波浪载荷数值计算结果的影响。为此，本文基于迁移矩阵法的模态计算结果计算得到了目标船在不考虑弯扭耦合模态下的波浪载荷，并把相应的数值计算结果放在同一张图中进行对比。

考虑到垂向模态和水平以及扭转模态不耦合，并且在水弹性统一方程中求解运动时，横向运动和纵向运动不耦合，所以在对波浪载荷进行数值预报时，弯扭耦合模态对垂向剪力和垂向弯矩的结果不会产生影响，如图7所示。

由图7可知，弯扭耦合效应对垂向载荷的数值结果无影响，峰值点所对应的频率有细微差异是二者在模态分析时存在的微小差异造成的。

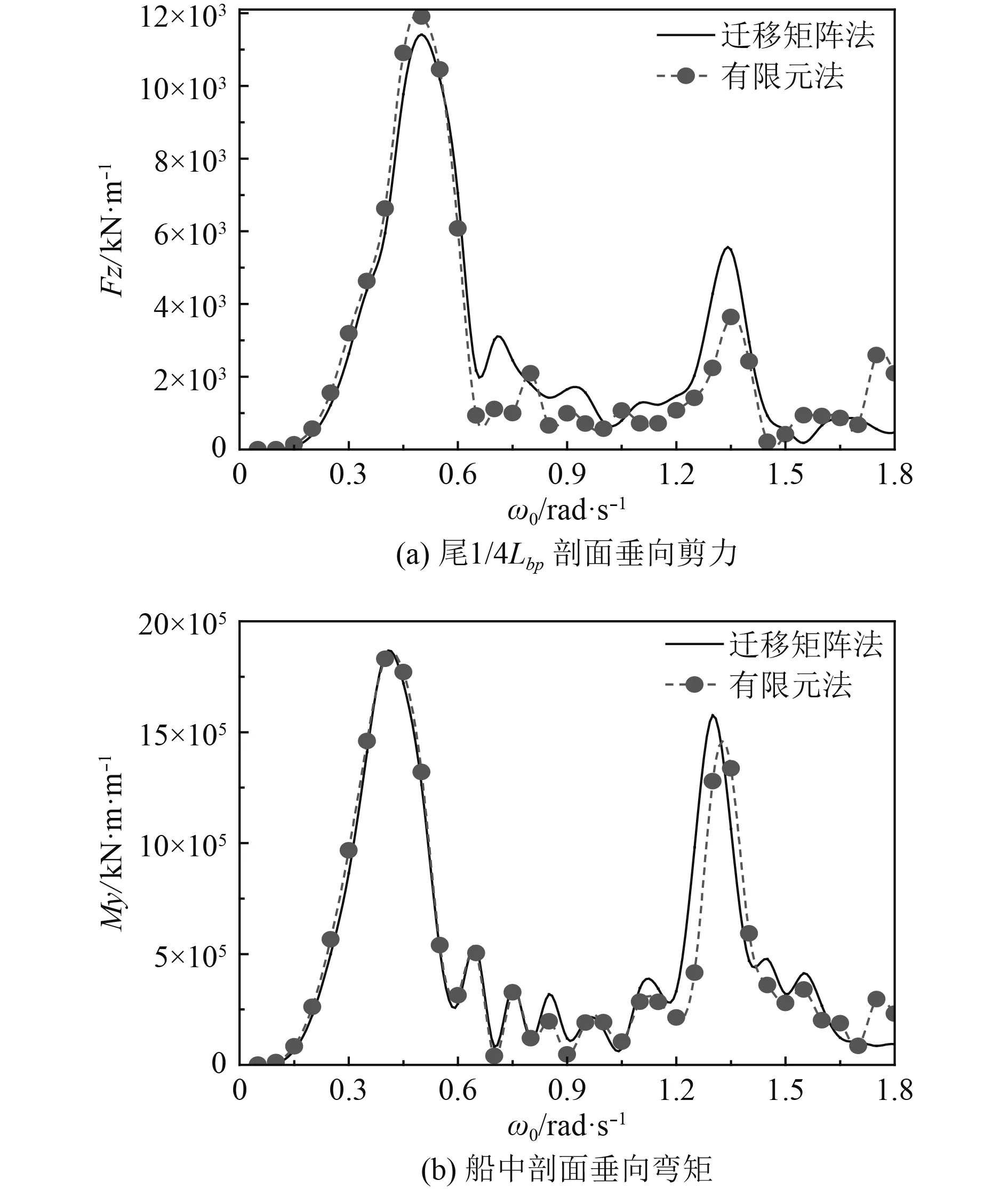
图 7 垂向载荷数值结果对比分析Fig. 7 Numerical comparison and analysis of vertical wave loads

图8展示了水平弯矩和水平剪力的数值对比结果，弯扭耦合模态对水平载荷的低频数值计算结果无影响；不考虑弯扭耦合模态时水平载荷计算结果在1.8 rad/s内不出现高频响应，由表2可知，不考虑弯扭耦合时所算得的水平弯曲固有频率太大，在上限为1.8 rad/s计算波浪频率范围内是无法激励船体产生高频响应的。然而，在考虑弯扭耦合模态时的水平载荷计算结果中，水平弯矩和水平剪力的高频响应峰值所对应的遭遇频率是和2节点弯扭耦合湿固有频率相对应的。

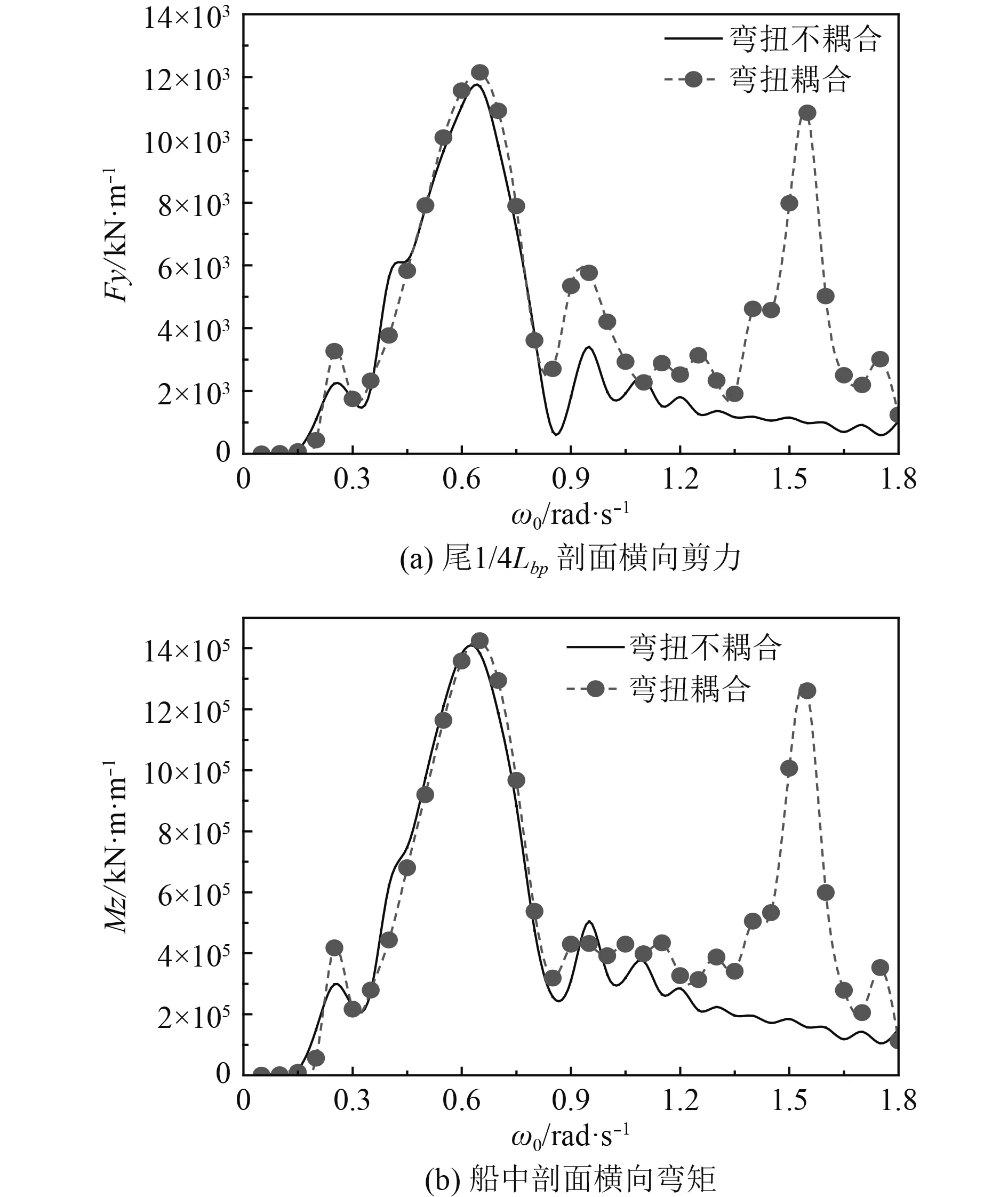
图 8 水平载荷计算结果对比分析Fig. 8 Numerical comparison and analysis of horizontal wave loads

由图9可知，二者的扭矩计算结果相差很大，且由表2可知，不考虑弯扭耦合模态时，船体扭转的干模态固有频率很低，导致所算得的扭矩高频响应（弹振成分）所对应的频率和低频扭矩所对应的频率范围十分接近,并且在自然频率为1.0 rad/s之后几乎没有扭矩响应产生，这些现象都不合理，因此可以得出结论：在计算超大型集装箱船波浪载荷时，不考虑弯扭耦合模态时，船体抗扭刚度低，扭矩的数值计算结果中高频弹振成分和低频成分会在自然频率很低时发生重叠，此现象不真实，因而可知计算结果不合理。

5 结 语

本文经过分析对比研究主要得出结论：超大型集装箱船的波浪载荷计算必须要考虑弹性体效应和弯扭耦合效应，具体结论如下：

1）超大型集装箱船的抗扭转刚度很弱，不考虑弯扭耦合时计算得到的船体扭转固有频率相当低；

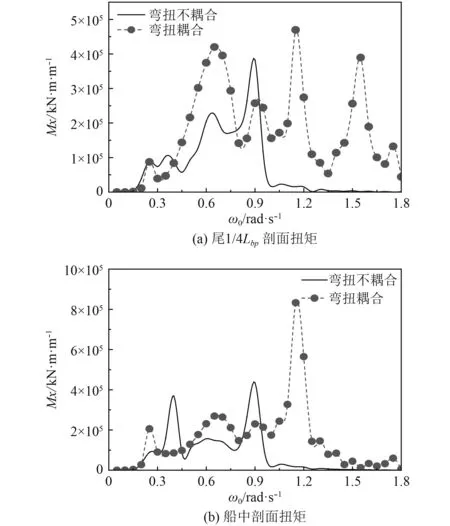
图 9 扭矩数值结果对比分析Fig. 9 Numerical comparison and analysis of torque

2）超大型集装箱船的弹性体效应十分明显，计算所得的波浪载荷的高频成分很明显，除扭矩的高频响应远大于低频响应外，其他载荷的高频弹振响应在数值上和低频响应处在同一水平；

3）对于超大型集装箱船来说，弯扭耦合模态对垂向载荷的数值计算结果无影响；

4）不考虑弯扭耦合效应时，水平载荷的高频响应数值结果不合理，而计算所得的纯扭转固有频率很低，导致扭矩中的弹振成分对应的频率和低频波浪激励扭矩所对应的频率十分接近，使得扭矩的弹振成分和低频部分在自然频率很低时就发生了重叠。