次分数跳-扩散过程下再装期权定价
2019-03-29王佳宁
王佳宁, 薛 红
(西安工程大学 理学院,陕西 西安 710048)
长期以来,金融工程学与金融数学研究的热点问题之一就是期权定价。美国经济学家Black、Scholes于1973年在文献[1]中开创性的提出了Black-Scholes模型,随后该模型很快就在各种期权定价问题中得到了广泛应用。文献[2]最先提出保险精算方法,从此期权定价问题就可以与等价的公平保费问题进行合理转化,而且把适用范围从均衡、完备、无套利的市场扩大到了非均衡、不完备、有套利的市场,大大简化了这类问题的解决过程。在文献[3-8]中保险精算方法的优越性得到了很好的体现。
最近几年,在金融证券市场不断发展过程中,许多在标准期权基础上变化、组合、派生而来的新品种不断兴起,即新兴期权。其中,在原来欧式看涨期权的基础上衍生出了一种新式的欧式看涨期权—再装期权,其特别之处在于:执行日前后期权持有者所持的欧式看涨期权不同。不过到期日并不发生任何改变,其数量是执行价格(被执行期权)与股票价格(执行日)之比,而执行日股票的价格就是执行价格[9]。文献[10-11]在分数Brown运动及相关随机分析理论的支撑下,构建相应数学模型,结合保险精算思想推得再装期权定价公式。文献[12]在股票价格满足跳-扩散过程的基础上,研讨再装期权在等价鞅测度条件下的定价问题,针对性给出对应的定价公式,并对数值模拟应用于实际提供了更便捷的方法。文献[13-15]指出了次分数Brown运动更具有一般性的Gauss过程这个特性,以及其有关概念、性质等,并在金融证券市场中有着广泛应用。本文将借助金融背景下次分数Brown运动和跳-扩散过程的数学模型,在保险精算方法以及随机分析相关知识帮助下,研讨再装期权的定价问题,导出其定价公式。
1 次分数跳-扩散过程下金融市场数学模型
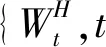

假定金融市场只有两种证券,一种是无风险资产即债券,其价格满足:
dMt=rMtdt。
其中Mt为无风险资产价格,r为无风险利率;另一种是风险资产即股票,其价格满足微分方程:
(1)
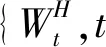
引理1随机微分方程(1)的解为
证明当在区间[0,t]内没有发生跳跃时,由次分数Ito公式可得
假定在t1∈[0,t]时刻内只发生一次跳跃,则在[0,t1)内有
同理在时刻区间(t1,t]内有
由(1)式有
当n→+时,可得所以
当跳跃次数服从Poisson过程时,可得
定义2[16]股票价格{St,t≥0}在[0,t]上的期望回报率βu,u∈[0,t],定义为
引理2股票价格{St,t≥0}在[t,T]上的期望回报率为
βu=μ,u∈[0,t]。
证明由引理1知
则
由
得
又由
得
所以
=1
故而
得证。
2 再装期权定价
定义3[10]假定到期日T之前只再装一次,则其收益结构为:在再装日期T1(0 当T1→T时,再装期权将退化为欧式看涨期权。 定义4[10]再装期权保险精算价格为 V=E{[exp {-μT1}ST1-exp {-rT1}K]I{exp {-μT1}ST1>exp {-rT1}K}} +E{[exp {-μT}ST-exp {-rT}K]I{exp {-μT1}ST1 其中无风险的资产按无风险利率r折现,风险资产按期望回报率β折现。 定理1次分数跳-扩散过程下再装期权保险精算价格为 其中 证明令 V1=E{[exp {-μT1}ST1-exp {-rT1}K]I{exp {-μT1}ST1>exp {-rT1}K}}, V3=E{[exp {-μT}ST-exp {-rT}K]I{exp {-μT1}ST1 假设在区间[0,T1]内出现波动跳跃J1(i),i=1,2,…,m,在[T1,T]内出现波动跳跃J2(i),i=1,2,…,n。 (1)计算V1,由于 则 V1=E{[exp {-μT1}ST1-exp {-rT1}K]I{exp {-μT1}ST1>exp {-rT1}K}} =E{E{[ST1exp {-μT1}-Kexp {-rT1}]I{exp {-μT1}ST1>exp {-rT1}K}|QT1}} 其中 V11=E{ST1exp{-μT1}I{ζ>d(m)1}}|QT1=m} (2)计算V2,由于 则 其中 (3)计算V3,由于 {STexp{-μT}>Kexp {-rT}}={γ>c(m,n)}, 则 V3=E{[exp {-μT}ST-exp {-rT}K]I{exp {-μT1}ST1 其中 本文是在金融背景下次分数Brown运动和跳-扩散过程的数学模型下加以研究推导的,可能与实际情况中股票价格变动还有一定差别,因此准确模拟金融证券市场十分重要,这需要我们在今后不断的研究过程中修正。


3 结 论
