基于滑动时步和预警阈值的双参数地音预警模型研究

陆 闯，夏永学，李 岩，陈法兵，王传朋，牛玉松

(1.煤炭科学研究总院 开采研究分院，北京 100013；2.天地科技股份有限公司 开采设计事业部，北京100013； 3.内蒙古伊泰广联煤化有限责任公司，内蒙古 鄂尔多斯 017299)

冲击地压是煤矿井下发生的较为严重的动力灾害之一，减少该类事故发生的主要手段之一是提高冲击地压监测预报水平，实现可靠的预测不仅可以使防治措施更有针对性，而且可以反过来促进冲击地压机理的发展。

目前我国冲击地压矿井采取了较多的监测方法，为防冲工作的开展提供了大量数据支撑，对冲击地压危险性预测具有重要的指导意义[1-5]：

(1)微震监测方法可以监测到煤岩体微破裂发展到一定程度而导致的最终破坏，能够较好反映采掘空间大范围内的能量释放情况，适合作为矿井区域中长期危险性评价的依据。

(2)应力与应变监测方法可以直观确定高应力、应变区域的变化趋势，由于其仍属于点监测手段，可靠的监测结果需要布置大量传感器，且监测结果的短期预警灵敏度不高。

(3)电磁辐射法能够反映煤岩体受力时变形与破裂的时变特征，但其采用的非接触式采集仪受井下变频设备的干扰影响大，预警准确度近期难以提高。

(4)钻屑法可以客观记录钻进时的动力效应(如声响、卡钻、吸钻、钻孔冲击等现象)，结合钻屑结果能够判断冲击地压发生的危险程度，但该方法劳动强度大，无法实现连续监测，评价结果受施工水平等因素影响较大。地音监测方法将传感器直接安装在监测区域的锚杆上，通过对煤岩体微破裂至失稳破坏前整个过程所产生的地音信息进行分析，可以根据地音活动规律确定煤岩体的损伤破坏程度，实现对冲击危险区域的提前预警和危险性评价。

目前，国内学者对于冲击地压地音监测方法的研究主要集中在地音危险性评价理论基础与前兆规律研究、预警效果分析方面[6-8]，但地音预警模型的优劣直接决定了预警结果的可靠程度，该方面研究相对缺乏。因此，本文拟通过对现场已有的地音数据统计分析，建立合理的地音预警模型并对其进行优化，以期提高地音对冲击地压的预警效果。

1 工作面概况及地音系统布置方案

内蒙古伊泰广联煤化有限责任公司红庆河煤矿3-1103工作面平均采深737m，走向长度3300m，倾向长度220m，煤厚平均6.35m，该工作面采用一次采全高的机械化综采方法。3-1103工作面新辅运巷北侧为已采的3-1101工作面采空区，两工作面之间布置有2个30m宽的双煤柱；工作面胶运巷南侧为尚未开采的实体煤。根据煤层冲击倾向性鉴定结果得知，3-1103煤层具有强冲击倾向性。该工作面安装有ARES-5/E地音监测系统，该系统可以实现对监测区域范围内震动频率为28～1500Hz、能量小于103J的地音事件进行实时监测[9]，系统组成结构如图1所示。

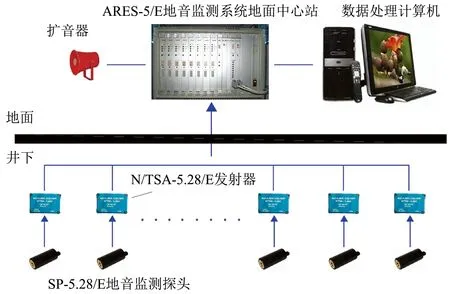
图1 ARES-5/E地音监测系统组成结构

对于工作面倾向长度大于200m时，地音监测系统要求在工作面前方的两侧巷道内至少各安装2个探头，探头距工作面40～200m。系统在工作面两侧巷道内各布置了2个地音探头，每个巷道内的2个探头分别距工作面70m和120m，具体布置方案如图2所示。随着工作面的推进，当工作面与其最近的地音探头相距20～40m时，将该探头挪至距工作面最远探头的前方50m，完成地音探头的交替挪移。该布置方案可以满足工作面前方250m危险范围内实时连续监测。

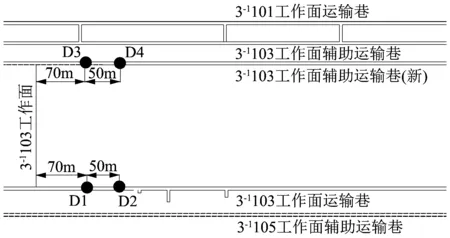
图2 3-1103工作面地音系统布置方案

2 地音预警模型的构建

2.1 预警指标的选取

ARES-5/E地音监测系统能够自动监测、记录单位时间的地音活动量(能量和频次)，考虑到地音预警往往持续数个小时，本文选取以生产班为单位时间的4个地音监测指标进行数据处理： 生产期间每班频次(FSW)；非生产期间每班频次(FSN)；生产期间每班能量(ESW)；非生产期间每班能量(ESN)。

确定地音监测指标之后，直接对监测指标设置不同的预警阈值构建预警模型，包括对以上4个监测指标设定不同的预警阈值，发现其评价结果具有一定的随机性，预报精度还有待提高。由于地音活动与煤岩体破裂阶段有关，地音前期的活动情况往往预示着后期的发展状态，在采用地音预测冲击地压时，可通过地音活动量的变化规律来实现预警。地音活动偏差值DEV是根据当前班次与相邻时间段内已发生的地音活动量平均值对照求得，一定程度消除了非常态地音活动引起的监测数据频繁起伏和随机误差的产生，因此能够反映一段时间内地音活动异常程度，可以作为冲击地压的地音预警指标。以生产期间地音生产班的频次偏差值计算为例，其预警指标值可表示为：

(1)

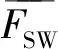
以此类推，可计算其余3个预警指标。

改变滑动时步n，通过顺序逐班增减已有地音监测数据以求得前n班的地音活动量移动平均值，可以作为当前班次地音活动量是否异常的参考值。n较小时，参考值易受偶然因素影响，预警结果具有一定随机性；n较大时，参考值受早期监测数据影响较大，不具备反映近期地音活动平均水平的能力，参考意义不大。因此，选择合理的滑动时步n，既需要减少近期数据的随机性，又可弱化长期数据的无代表性。从监测数据的时效性角度出发，在研究预警模型初期，n分别取3，4，5，…，10步[10-11]。

2.2 预警规则的制定

地音监测的对象是采掘空间一定范围内的高频低能震动事件，属于局部监测方法。以往选择的地音预警对象为高能微震事件[12]或者现场反馈的煤炮事件[13]，但是部分高能微震事件发生于高位岩层或者距离地音探头较远的平面区域，已经超出了地音的有效监测范围；煤炮虽然发生在监测区域附近，但其释放能量的强弱只能靠人的感官判断，受人为因素影响较大，单方面考虑其中一种情况作为地音预警判别对象会产生较大误差。因此，本文为提高预警模型准确度，采用现场发生的微震能量大于4次方且具有动力现象(煤炮、震感、气流等)的事件(记为冲击显现事件)作为地音预警的对象。

地音预警的实用性在于可以提前预知冲击危险的来临，能够为防冲工作的开展争取时间，预警时间过短无法及时采取措施避免人员伤亡，预警时间过长必然影响矿井实际生产。参考文献[2]中提出的冲击地压预报效能R值评分法可知，预警周期过长，随机预报的成功率越大，地音的预报效能越低。因此，本文规定冲击显现事件发生前至少1班并且不超过3班的预警记为报准；预警发出后3班后未发生冲击显现事件或者发生冲击显现事件3班后仍然预警记为误报；对于发生了冲击显现事件，但是前3班内未提前预警的记为漏报。地音预警模型中3种状态的关系如图3所示。

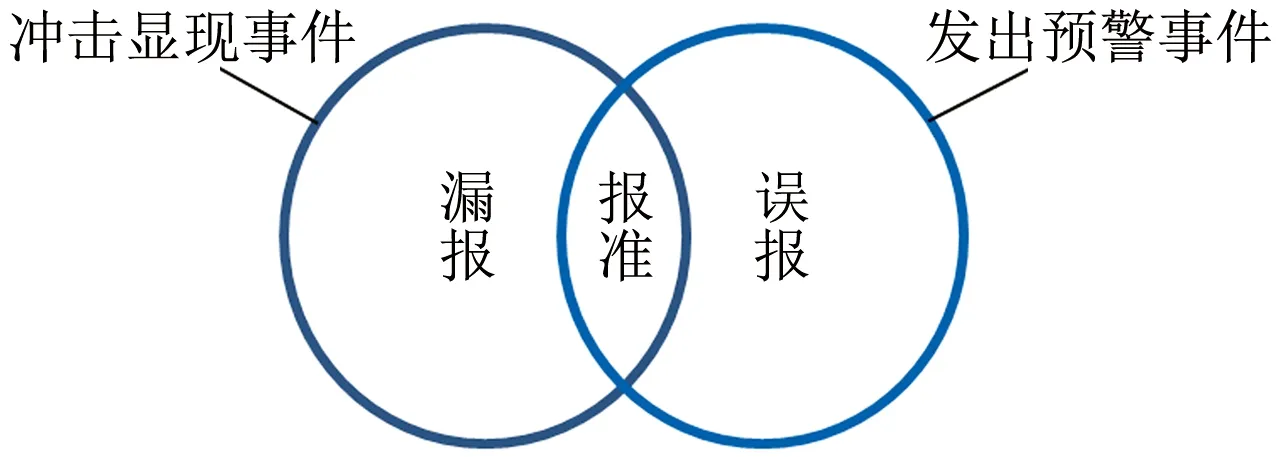
图3 地音预警模型3种状态关系

预警阈值DEV0作为是否触发预警事件的重要条件，认为预警指标达到阈值DEV0以上即为预警。DEV0的确定原则上既要防止误报又要避免漏报，同时还可以提高报准[14]，在研究初期DEV0分别取30%，40%，…，100%作为预警模型效果初步分析的基础条件。下文将通过对预警结果统计分析，最终确定预警模型双参数(n,DEV0)的最优组合值。

3 预警结果统计与分析

选择2018年9月1日至2018年11月30日期间，3-1103工作面辅运巷内D3探头在其监测区域内的预警情况进行分析。在此期间共发生20起冲击显现事件，主要集中在9月和11月份，10月份相对较少，事件情况如表1所示。

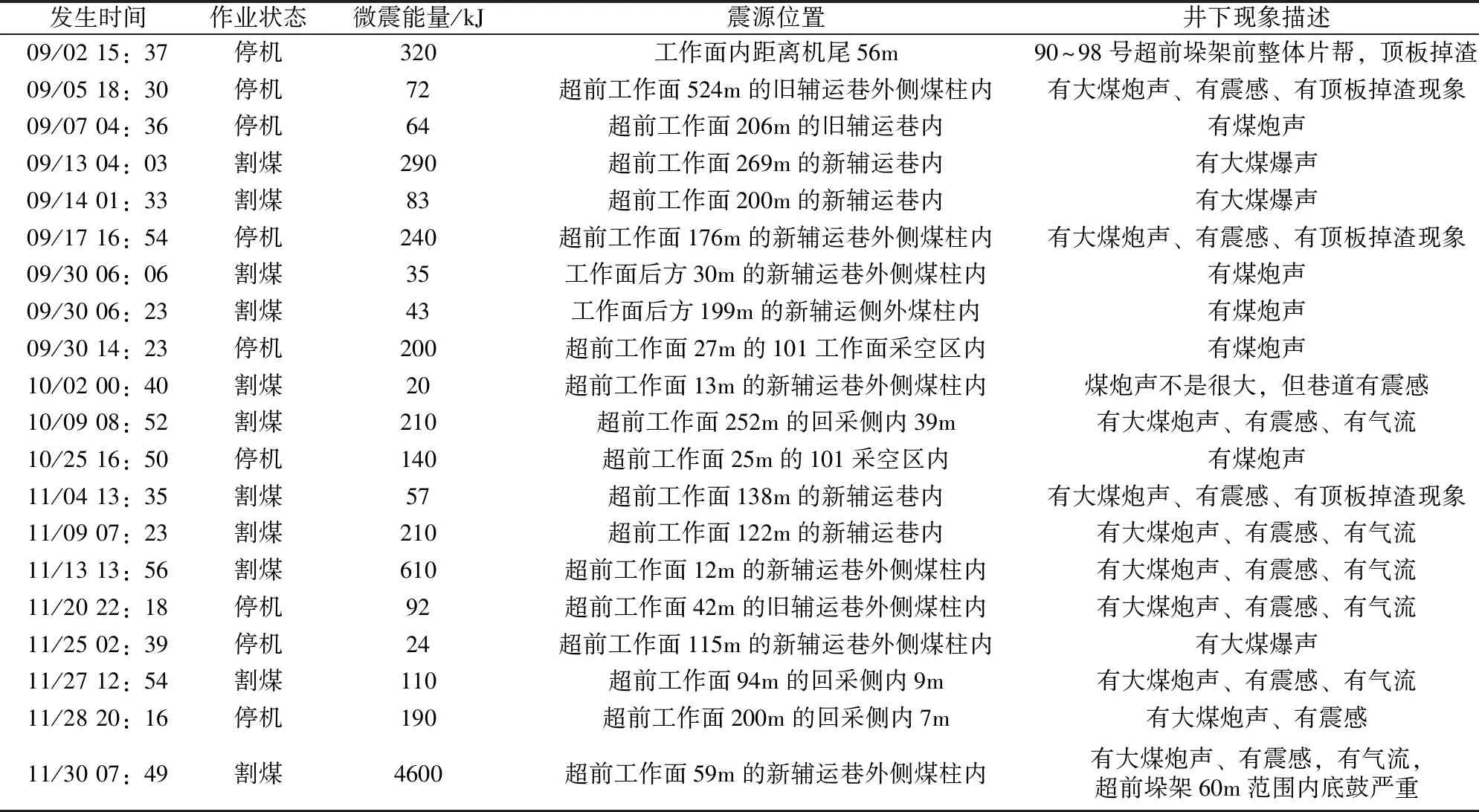
表1 研究区域冲击显现事件

基于3个月监测的数据绘制出地音活动量偏差值随时间的变化曲线，如图4所示(图例含义：字母e和f分别表示班能量和频次，数字为滑动时步n)。由图4可知，基于不同n值的偏差值曲线分散度较高，但大体走势一致。结合生产班与非生产班整体分析，当选择合适的(n,DEV0)组合时，9月和11月份的地音预警次数将多于10月，这与现场冲击显现事件发生时间相吻合。

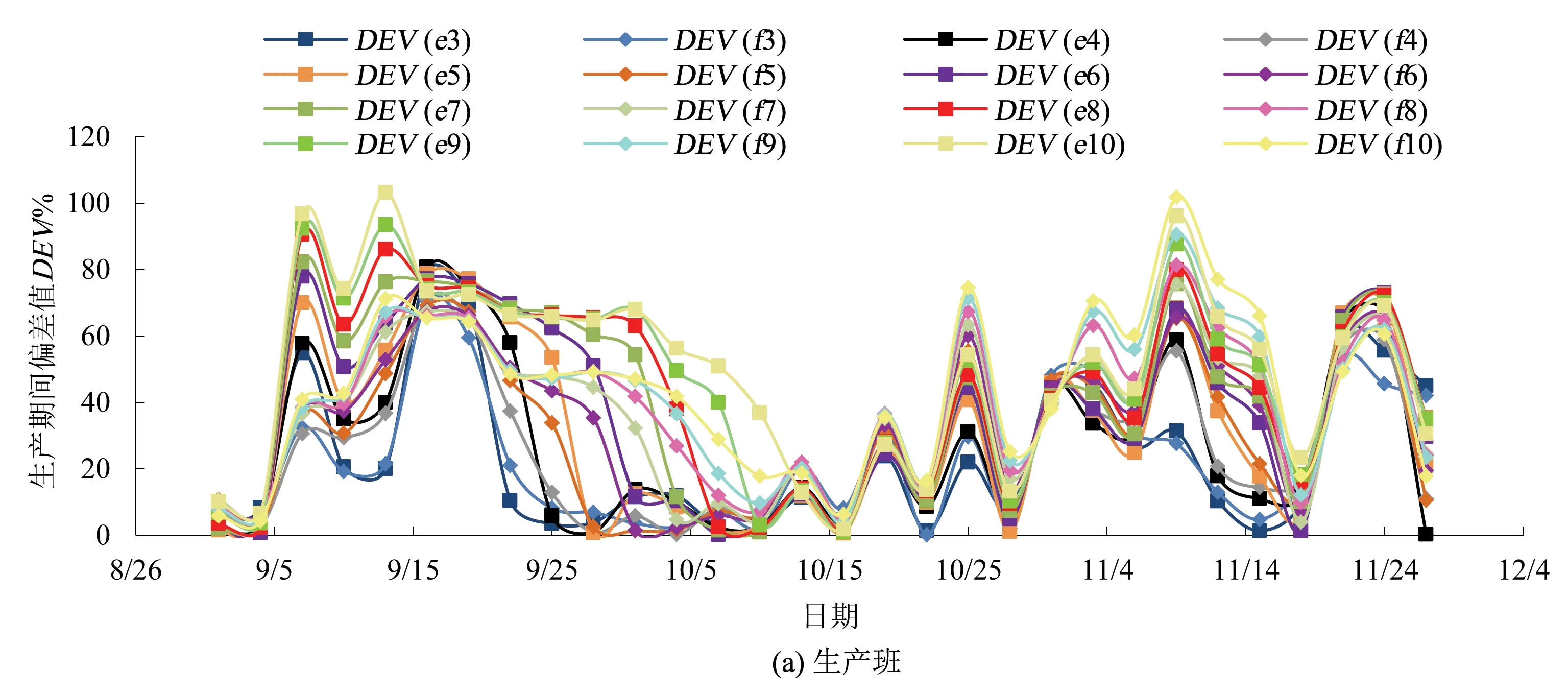
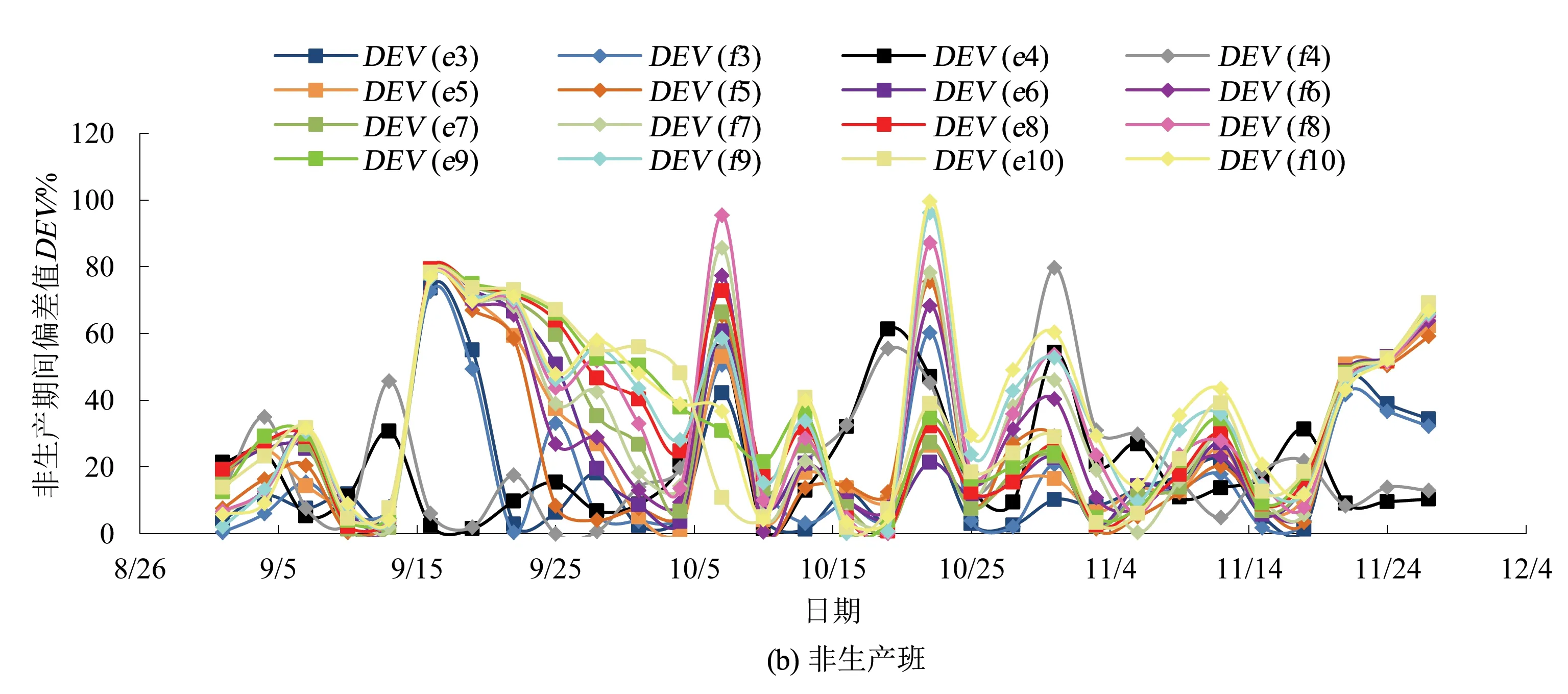
图4 研究期内地音活动量偏差值随时间的变化曲线

3.1 报准率p1与漏报率p2分析

报准事件和漏报事件互为对立事件，报准率p1是指冲击报对次数与发生冲击显现事件总数的比值，漏报率p2为冲击未报次数与发生冲击显现事件总数的比值，两者之间关系为：p1+p2=1，因此选择报准率p1进行分析。

表2为3个月内基于不同(n,DEV0)组合的地音报准率分布。从表2可知，DEV0一定时，报准率整体随n增加而增加，n一定时，报准率整体随DEV0的增加而减小。当DEV0选取的过低，降低了预警的门槛，虽然报准率较高，但也容易提高误报率；在DEV0处于较高水平时，虽然剔除了大量误报，但也使得报准大大降低。

由于报准率同时受n和DEV02个参数影响，为了确定影响报准率的主控因素，优化报准率水平，对以上2个参量进行多因素无重复方差分析。假设表2中任意一组(n,DEV0)所对应的报准率大小为Xij(i，j分别为行、列数)，且服从Xij～N(μij,σ2)正态分布，各Xij相互独立，μij，σ2分别为与正态分布相关的参数。经计算可得其方差分析结果，如表3所示，n和DEV02个参数所对应的F值都大于其临界值，说明两者对报准率均有显著影响，但与n相比，DEV0所对应的F值远大于其临界值，对报准率有极显著影响，是影响报准率的主要因素。

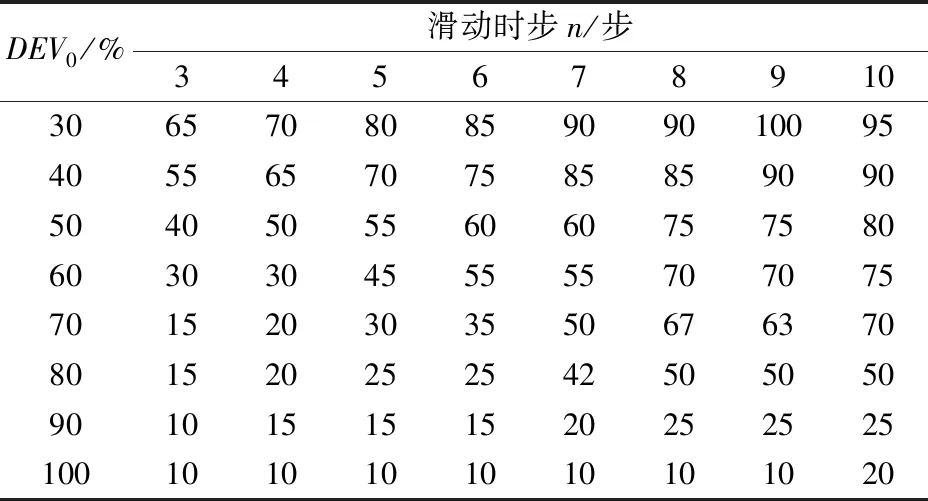
表2 基于不同 (n,DEV0)组合的报准率分布

3.2 误报率p3分析

误报率p3是指地音预警但未发生冲击的次数与总触发预警次数的比值。统计得出不同(n,DEV0)组合下的误报率如表4所示，地音总体误报率低于50%。DEV0取较低水平时，误报率受n影响较小，基本保持在同一水平；DEV0介于50%～70%时，误报率随n同步增加，之后稳定在一定水平；DEV0高于70%时，在n起步时，地音系统没有误报，之后误报率随n增加而增加。n一定时，误报率整体随DEV0的增加而减小。

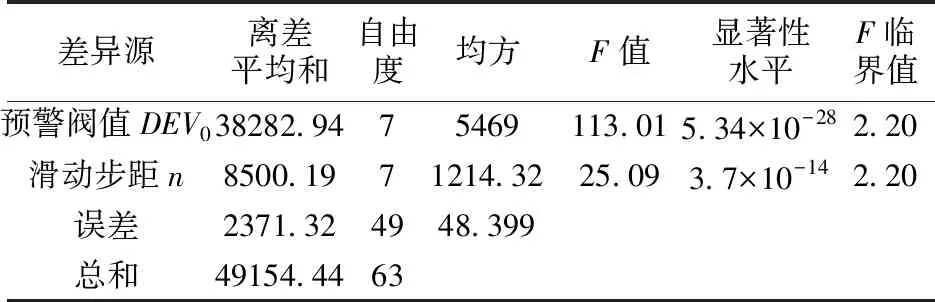
表3 影响报准率的n，DEV0双因素无重复试验方差分析结果

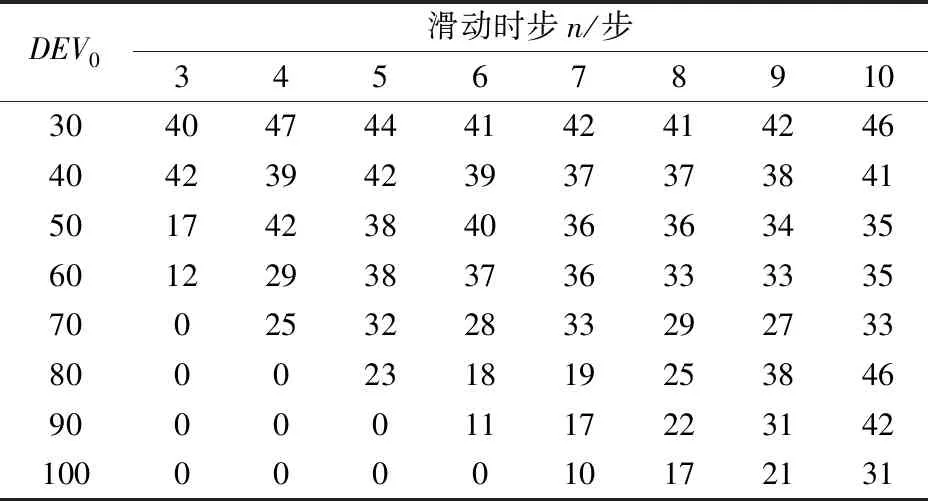
表4 基于不同(n,DEV0)组合的误报率分布 %

同样对影响漏报率的n，DEV02个参数进行多因素无重复试验方差分析，结果如表5所示。n，DEV0对误报率均有显著影响，但DEV0对误报率的影响更为显著，是影响报准率的主要因素，该结果与报准率的主要影响因素相同。

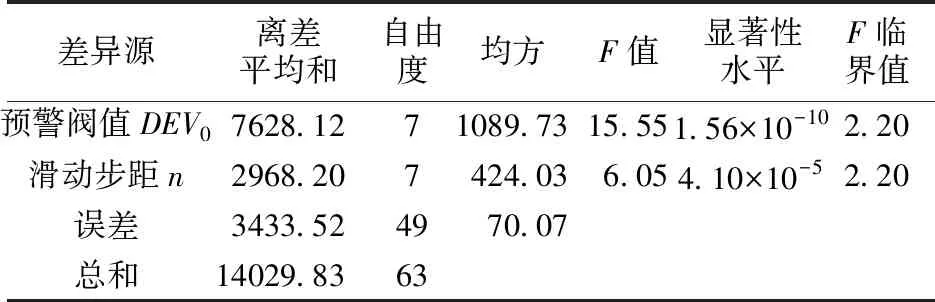
表5 影响误报率的n，DEV0双因素无重复试验方差分析结果

3.3 预警模型最优值求解

预警模型的优劣需要用报准率p1和误报率p32个指标共同衡量。上已述及，DEV0是影响报准率和误报率的主要因素，但改变DEV0会使报准率和误报率这2个目标值沿相同方向改变，即降低DEV0会使报准率和误报率同时提高，提高DEV0会使报准率和误报率同时降低，2个分目标值不能同时被优化。针对以上问题，为得到最优预警模型，需使用双目标函数值最优化方法求解[15-16]。

首先，建立与报准率和误报率相关的效用加权目标函数：

(2)

其中，p1=f1(n,DEV0),p3=f2(n,DEV0),ωi为效用权重系数。

s.t.n=3，4，5，…，10。

DEV0=30%，40%，50%,…，100%。

0≤p1，p3≤1

此外，根据实际生产需要，常需要使分目标函数p1和p3控制在一定合理区间内方具有使用价值，故本模型要求报准率不低于40%，误报率不高于30%。因此以上目标函数又增加了2个价值约束条件：p1≥40%；p3≤30%。

根据表2和表4绘制不同DEV0条件下的p1，p3随n的变化曲线，由价值约束条件得，图5的可行域为红线以上曲线标记点所对应的(n,DEV0)组合，图6的可行域为红线以下曲线标记点所对应的(n,DEV0)组合。结合两图初步得出满足目标函数的5个非劣解，如表6所示。

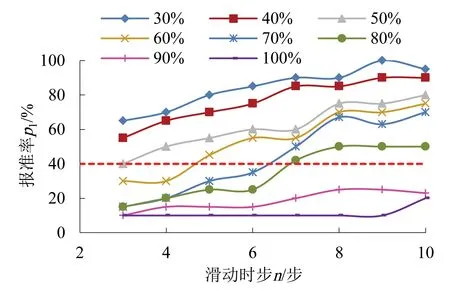
图5 不同DEV0条件下p1随n的变化曲线

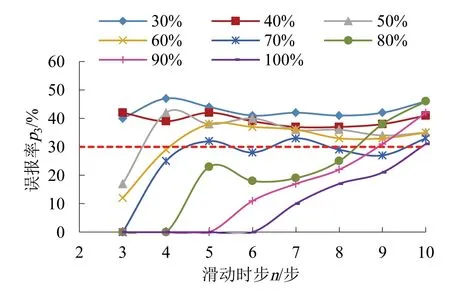
图6 不同DEV0条件下p3随n的变化曲线

(n,DEV0)(5,30%)(8,70%)(9,70%)(7,80%)(8,80%)p1/%4067634250p3/%1729271925

p1，p2均是与效用有关的分目标函数，根据以上5组非劣解对应的分目标函数值对效用权重进行等比打分，打分结果如表7所示。

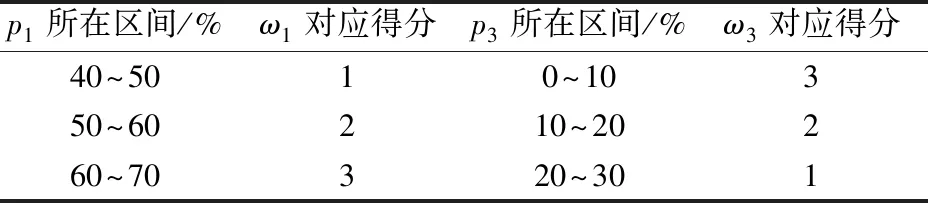
表7 效用权重打分

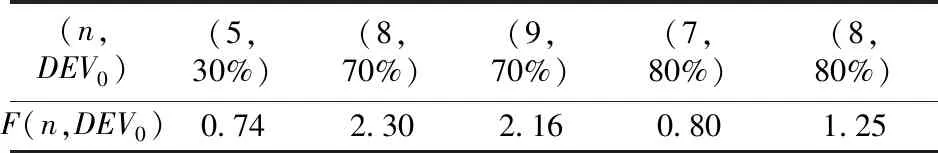
表8 效用权重目标函数解集

4 结 论

(1)根据地音预警原理，选取了地音活动偏差值DEV作为地音预警指标，分析得出滑动时步n的选取是衡量预警指标的时效性依据。从地音预警的实用性角度出发，制定了地音预警原则，确定了以不同(n,DEV0)组合优化预警模型的思想。

(2)基于地音预警原则对地音预警的报准率、漏报率和误报率进行统计，通过对影响报准率和误报率大小的(n，DEV0)进行多因素无重复试验方差分析，得出两者对地音预警效果均具有显著影响，其中DEV0是主要影响因素。采用效用加权的双目标函数最优化方法，求得双参数预警模型的最优解为(8，70%)组合，其对应的地音预警效果分别为报准率67%，漏准率33%，误报率29%。