基于高中数学学科核心素养的课程评价
2019-03-28江苏省张家港高级中学丁亚萍
☉江苏省张家港高级中学 丁亚萍
在高中数学中,对于核心素养的培养非常重要.核心素养的培养,主要取决于对课程的见解.而课程评价则能够驱动课程见解.进行核心素养课程方面的研究,可以帮助教师提高课程质量.教师可以找到培养核心素养的有效途径及方法,使得对核心素养的培养更加便于实施.
当前阶段,对核心素养的探索指出:核心素养的最终实现,需要在课程中进行,在数学学科当中,课程评价是课程与核心素养对接当中非常重要的一个步骤.因此,本文主要研究基于核心素养的课程评价.[1]
一、教学课程与核心素养的联系
在研究两者之间的联系时,首先需要清楚这两者的具体概念,而这两者的主要概念不是三言两语能够解释清楚的.但是从最基本的角度来讲,还是可以理解的.课程标准主要是从六个方面来解释核心概念的.除此之外,笔者认为其最终需要认识到学生“必备品格”与“关键能力”的重要性,用比较通俗的话来理解,就是“用数学教学生”,这句名言应当成为高中数学教师在进行数学教学的过程中需要研究的具体方法.
例如,在进行“函数的单调性”这一课的教授时,怎样才能够做到“用数学教学生”呢?又怎样将这一理念与核心素养进行对接呢?对于这些问题的答案,笔者理解为:函数的具体作用就是对事物之间的关系进行描述,当这些事物具有某一特征时,就符合函数的单调性原理,可以将其看作在特定的区间内具有一定变化的数学模型.数学模型所具备的作用就是将生活中具有某类特征的事物表示出来.
如运用函数模型解决生活中的物理问题,抛物线就是可以很好地解决物理问题的函数模型:
例1 轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图1,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台E上,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图1所示的直角坐标系,x轴在地面上,助跑道一端点为A(0,4),另一端点为C(3,1),点B(2,0),单位:米.求助跑道ABC所在的抛物线方程.
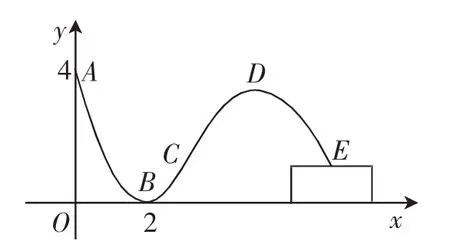
图1
例题答案:设助跑道ABC所在抛物线方程为f(x)=a0x2+b0x+c0.

所以助跑道ABC所在的抛物线方程为f(x)=x2-4x+4.
采用这种方法进行教学,能够体现出数学课程的本质所在.根据这一原理,数学就完成了课程与核心素养的对接.所以各个地区在进行对核心素养的探究时,都会比较重视知识与现实生活的联系.
二、基于核心素养的课程评价
根据上文的论述,在进行核心素养的课程评价的探讨过程中,就有了能够依据的基础,探讨可以从以下几个方面进行:
首先,需要注重意识的培养.意识在行动之前,可以说是先导要素,只有先有了意识才能进行具体的行动.对于高中数学课程中所需要的核心素养意识,需要从核心素养角度进行具体的实施.比如,在进行函数单调性学习时,教师需要先想到怎样才能够使得学生了解到函数单调性在生活当中具有一定的作用.[2]根据这一想法,教师的教学过程就变得非常清晰了.教师能够让学生在进行学习之前先在生活中找一些具有函数关系的例子,然后让学生对例子中变量的变化对函数变化产生的影响进行分析,让学生用自己的语言进行描述.如展示出城市气温变化曲线图,如图2所示,并提出以下问题:随着时间的变化,温度的变化趋势是怎样的?(“上升”“下降”)
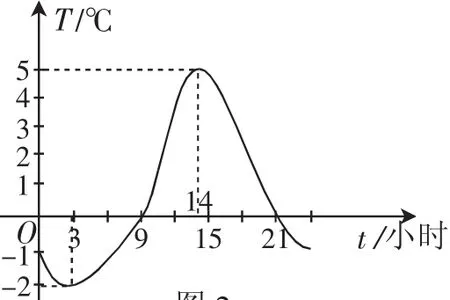
图2
由于学生知道了实际的例子,教师在进行讲解的时候,学生就会更加容易理解.这时教师再进行针对性练习,通过图像让学生判断函数的单调区间,如图3所示.
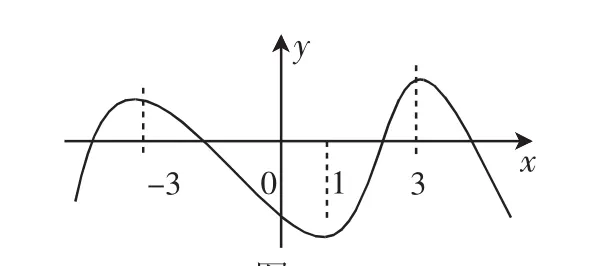
图3
其次,对于教学过程的设计,主要可以分成以下两个方面的取向:(1)依照课程标准中所列出的九个概念进行教学的设计;(2)依照学生的思维进行课程的设计.笔者比较偏向于后者,但是依据第一个取向对教学进行设计,能够更加关注教学的细节,推动学生思维的发展.
最后,从教学最终呈现出来的结果进行核心素养在课程中实施情况的反推.教师在课堂结束后进行教学反思是研究课堂的必要步骤,教师通过对教学过程的反思,能够更清楚地了解到学生素养的培养情况.在对函数单调性这一知识点进行学习的过程中,将实际事物中非数学的部分剖离出去,采用函数的方法对问题进行解决.[3]在进行这些步骤的时候,一定会考查到逻辑思维能力及想象能力.有时候还需要进行数据分析的运用,这样在六个概念中已经具备了五个.再加上学生在进行函数单调性的应用时,需要结合实际情况进行,如可以运用函数的单调性判断实际问题中的最大值、最小值等,通常都会出现在利润、成本、面积求和等问题中.
例2 工厂生产某种产品,次品率p与日产量x(万件)间的关系为:
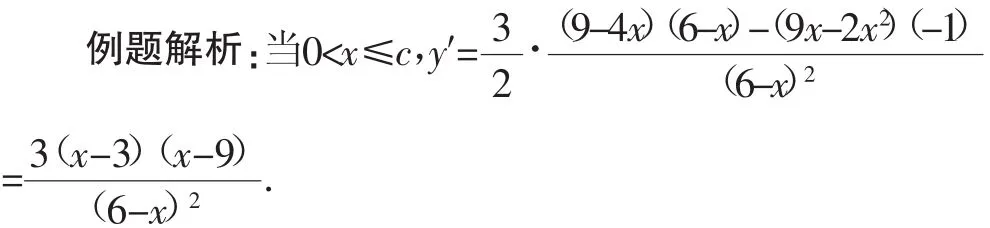
①当0
②当3≤c≤6时,在(0,3)上,y′>0为增函数,在(3,c)上,y′<0为减函数,所以当x=3时
通过以上问题的解决,使学生认识到数学的重要作用,将数学与实际联系起来,这是形成数学素养所必备的能力及条件.
经过上述三个方面的实施规则,核心素养的评价便有据可依.
三、数学作为工具学科的课程融合评价
学科融合是核心素养的课程评价的另外一个重要内涵.核心素养可以看作综合能力的体现,既然这种能力具有综合性,那么单一的学科学习则不能够满足其培养的要求.对于数学来讲,数学在教育当中可以看作一门基础性的且必须了解并掌握的学科,高中数学教师需要具有学科融合的意识,发现数学与其他学科之间的联系,包括与物理、化学等学科的共通之处.这样才能够保证在构建核心素养时,有效地与别的学科进行融合.
根据“一切历史都是当代史”的观点,在进行数学学习的过程中,会遇到运用文学史等内容的知识,这些知识之间的贯通性能够帮助学生了解及掌握数学知识.特别是针对高中数学较为复杂的结构来讲,这一定是具有核心素养内涵的教学指向.
