回归教材，追根溯源——谈高三数学复习策略

☉江苏省海安高级中学 张 梅

一、问题的提出

在高三数学复习中，必须有针对性地选取一段时间（一般是一轮复习中），重拾课本，回归教材.笔者结合教学实践，就高三数学复习中回归教材的一些做法做了一个简单的梳理，以期抛砖引玉.

二、问题的解决

在高三数学复习过程中，一定不能脱离高中数学教材，要以数学课本为指引，真正做到重拾课本，回归数学教材，深入数学教材，用好数学教材，深化数学教材，重视高中数学知识体系，为数学基础知识、基本方法和基本技巧的学习打下良好基础.

1.重温数学公式，提升认知高度

数学公式是数学概念、数学结论等的本质体现，应系统重温数学公式和定理，从理论层面和科学高度来引领高三复习.《高中数学课程标准（实验）》中明确要求“理解基本的数学概念、数学结论的本质，了解概念、结论等产生的背景、应用，体会其中所蕴含的数学思想和方法，以及它们在后继学习中的作用”.

因而，在高三数学的复习过程中，不仅要重温基本的数学公式和定理，还要适当引领学生去关注相应公式和定理的来龙去脉、多样化的推导过程，以及其中所蕴含的丰富的数学思想和方法，这也是数学公式和定理的核心价值所在.

例1普通高中课程标准实验教科书《数学·必修5·A版》（人民教育出版社，2007年1月第3版）第18页练习第3题：（三角形射影定理）

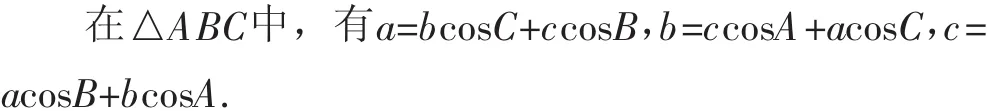
公式特征：在解三角形问题中离不开正弦定理与余弦定理，而三角形射影定理也是其中一个重要的公式.三角形射影定理可以巧妙并迅速地解决有关三角形中“两边及各自对角的余弦与第三边的关系”相关问题.结合三角形射影定理的公式特征，记住其对应关系，同时，在解题过程中，还要适当掌握三角函数的配凑技巧，正确利用三角恒等变换来处理问题.

对比真题：（2017年全国卷Ⅱ文·16）△ABC的内角A，B，C的对边分别为a，b，c，若2bcosB=acosC+ccosA，则B=______.

分析：根据题目条件中的“2bcosB=acosC+ccosA”，结合射影定理的公式特征，考虑到涉及两边及各自对角的余弦与第三边的关系加以转化，进而得到cosB的值，从而得以求解角B的大小.

解：结合射影定理，并利用条件2bcosB=acosC+ccosA，可得2bcosB=b，化简得cosB=.

设计意图：在解决数学问题时，正确掌握相应的数学公式或定理，可以快速、简捷地解决一些相关的数学问题，进而省去盲目的推理论证过程，为考试节约宝贵的时间.同时重温了数学公式或定理，也进一步复习了相关知识，真正提升了认知高度，进而从更高的层面来处理与解决问题.

2.整合教材例（习）题，掌握通性通法

教材中例（习）题的编排方式主要有两种：

（1）通过呈现综合应用背景的题目来指导学生在该模块的知识条件下加以分析、解决与应用，从而实现相关知识间的融会贯通.

（2）通过不同章节题目的统一呈现，有时还可以有针对性地进行变形、转化与拓展，在灵活多变的问题情境中来解决问题，强化通性通法.

这就要求教师深入研究教材，科学联系并选取教材中富有价值的典型例（习）题，夯实基础，掌握通性通法，并在此基础上尝试多思维角度分析，以及多方法解决，加强思维转换能力，注重知识的横向与纵向联系，培养学生的发散性思维，形成思维的创新性与创造性.

例2 普通高中课程标准实验教科书《数学·必修4·A版》（人民教育出版社，2007年2月第2版）第二章《平面向量》.

例题特征：平面向量既有“数”的因素，又有“形”的思维，解题思路往往可以从“数”与“形”的“两面性”方面加以展开，提高识“图”、用“图”能力，拓展用“数”、解“数”思维，真正强化数形结合思想在平面向量问题中的应用.从而确定解决此类问题的通性通法，可以通过坐标法来进行“数”的运算，也可以通过几何法来进行“形”的转化，进而达到最终目的.

对比真题：（2018年浙江卷9）已知a，b是平面向量，e是单位向量.若非零向量a与e的夹角为，向量b满足b2-4e·b+3=0，则|a-b|的最小值是（ ）.

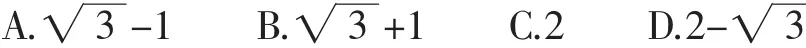
分析：结合题目条件，解题思路可以从“数”的方面或“形”的方面加以展开，从不同角度切入会有不同的解决方法.

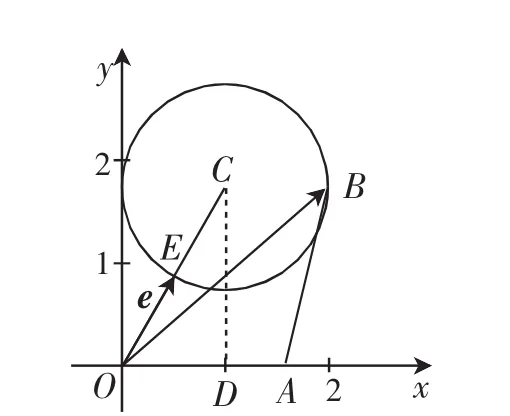
图1

设计意图：与平面向量的数量积有关的计算问题一般有两种常见的通性通法：一是根据平面向量基本定理，在图形中选取恰当的基底，将所要求解的向量表示为基底的线性组合，然后利用基底法来解答；二是通过建立恰当的平面直角坐标系，将所涉及的平面向量坐标化，进而利用坐标运算来解答.这是两种常见的通法，而结合几何图形的特征，通过数量积的定义以及几何意义（投影法）来处理也是比较有特色的，而选择极化恒等式来处理，往往会更加简单快捷.当然，其中也有其他相应的通性通法，可以根据不同的知识点进行合理有效的归纳.

3.培养数学品质，凸显一题多变

高考最终的PK实际上就是综合数学品质的PK，而通过高三数学复习来有效培养与提升数学品质是解决问题的关键.

一题多变是在有效思考、探究的基础上，从一个熟悉的基本题型入手，通过不断改变题设中的某些关键条件或相关的结论，将相近的问题串联起来，让学生形成强烈的系统认知冲突与知识应用，突出知识的交汇与融合，进而真正达到强化学生的学习基础、增强学习应用、提升学习效率，培养学生细心谨慎的学习习惯，以及创新意识与能力.

因此，在高三数学复习中，通过回归教材，品味教材中浓厚的数学品质与核心素养的所在，真正有效地利用教材，并发挥教材的全部功效，来服务我们的学生.

三、感悟与反思

其实，在高三数学复习过程中，我们不能只是片面地利用相关的教辅资料按高中数学的知识点体系把题目进行简单的归类与应用，而应该在数学复习过程中从高中数学教材入手，追根溯源，构建起高中数学相关知识的网络体系与框架，挖掘知识的本源，渗透数学相关的思想方法和核心素养，让数学复习真正为高考提供有效的动力支持.F