你若盛开，数列自来——一道数列最值题的探究

☉山东省枣庄市第三中学 朱信富

数列在高中数学中“叱咤风云”，独树一帜，既有函数的特征，又有自身的规律，而且具有深远的内涵与丰富的外延，特别在应用中显示出了独特的魄力和势不可挡的渗透力，备受各个层面的命题者的关注．从近几年新课标高考试题来看，数列中的最值问题越来越成为高考命题的热点之一，真正体现了数列与方程、函数、不等式性质及相关知识的应用，充分展示了其所形成的知识交汇与纽带的作用．

问题 （2016年江苏省南京一模）设Sn是等比数列{an}的前n项和，an>0，若S6-2S3=5，则S9-S6的最小值为______.

本题以等比数列的前n项和为问题背景，通过等比数列的前n项和的一个关系式的给出来确定相应的涉及等比数列的前n项和的关系式的最值问题.用数列与函数的关系来设置问题，通过确定数列的最值问题来落实，可以巧妙结合题目条件，利用等比数列的通项公式、前n项和公式及相关的性质，从不同的思维角度出发，进而利用不同的方法来解决.

结合已知条件S6-2S3=5，利用等比数列的前n项和公式加以转化，整理得到可得q>1，进而再次利用等比数列的前n项和公式把S9-S6转化为含有q的关系式，结合关系式的等价变换，并借助基本不等式来确定最值.

解法1：设等比数列{an}的公比q>0，且q≠1.

结合已知条件S6-2S3=5，利用等比数列的通项公式加以转化，得到（q3-1）（a1+a2+a3）=5，可得q>1，进而再次利用等比数列的通项公式把S9-S6转化为含有q的关系式，结合关系式的等价变换，并借助基本不等式来确定最值.

解法2：设等比数列{an}的公比q>0，且q≠1.

所以S9-S6的最小值为20，故填答案：20.

结合已知条件S6-2S3=5，利用等比数列的通项公式加以转化，得到（q3-1）（a1+a2+a3）=5，可得q>1，结合关系式的等价变换并利用等比数列的通项公式把S9-S6转化5为含有q的关系式，然后结合关系式的等价变换，并借助基本不等式来确定最值，最后利用不等式的性质来确定S9-S6的最值.

解法3：设等比数列{an}的公比q>0，且q≠1.

则有S9-S6≥20，即S9-S6的最小值为20，故填答案：20.

根据数列的函数性质引入参数A得到Sn=Aqn-A，结合S6-2S3=5得到参数A关于q的表达式，进而利用数列的函数性质并结合代换法把S9-S6转化为含有q的关系式，最后结合关系式的等价变换，并借助基本不等式来确定最值.

解法4：设等比数列{an}的公比q>0，且q≠1.

在等比数列{an}中，根据数列的函数性质有Sn=Aqn-A，其中A≠0.

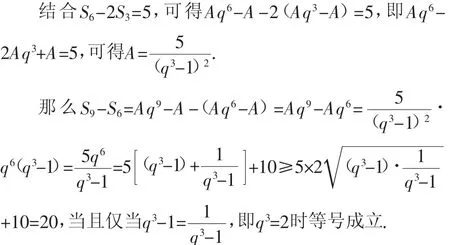
所以S9-S6的最小值为20，故填答案：20.

结合等比数列的性质得到S3，S6-S3，S9-S6构成公比为q3的等比数列，再结合S6-2S3=5得到可得q>1，然后结合等比数列的通项公式把S9-S6转化为含有q的关系式，最后结合关系式的等价变换，并借助基本不等式来确定最值.

解法5：由于等比数列{an}中，an>0，则有Sn>0.

由S6-2S3=5，可得（S6-S3）-S3=5.

由等比数列的性质知S3，S6-S3，S9-S6构成公比为q3的等比数列.

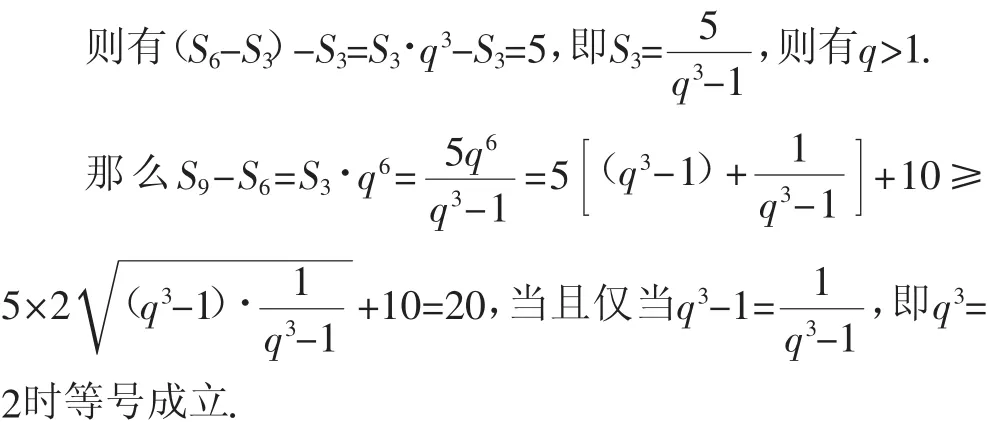
所以S9-S6的最小值为20，故填答案：20.

结合等比数列的性质得到S3，S6-S3，S9-S6成等比数列，进而建立相应的关系式，并结合S6-2S3=5代入转化为含有S3的关系式，最后利用关系式的转化并借助基本不等式来确定最值.

解法6：由于等比数列{an}中，an>0，则有Sn>0.

由等比数列的性质知S3，S6-S3，S9-S6成等比数列.

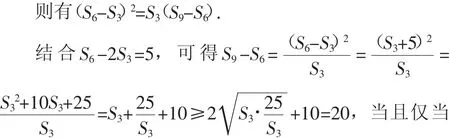
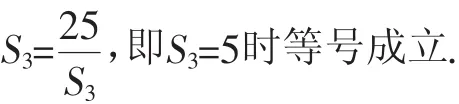
所以S9-S6的最小值为20，故填答案：20.

结合等比数列的性质得到S3，S6-S3，S9-S6成等比数列，进而建立相应的关系式，并结合S6-2S3=5代入转化为含有S3的关系式，最后直接借助基本不等式来确定最值.

解法7：由于等比数列{an}中，an>0，则有Sn>0.

由等比数列的性质知S3，S6-S3，S9-S6成等比数列.

所以S9-S6的最小值为20，故填答案：20.

结合等比数列的前n项和的性质Sn+m=Sn+qnSm，通过S6-2S3=5的转化得到关系式，可得q>1，再利用相关性质转化S9-S6为含有q的关系式，结合关系式的等价变换，并借助基本不等式来确定最值.

解法8：由于等比数列{an}中，an>0，则有Sn>0，设等比数列{an}的公比q>0，且q≠1.

所以S9-S6的最小值为20，故填答案：20.

总评：解决等比数列的前n项和的关系式问题，关键是结合通项公式、前n项和公式或等比数列的基本性质加以转化，再根据所确定的关系式的特征，利用基本不等式来确定最值.特别是在利用基本不等式时，要注意前提条件中“正数”的确定，这也是解决此类问题时比较容易忽视的地方.

涉及数列中的最值问题，往往思维方式各异，求解方法多种多样，而且数列性质与公式的运用技巧灵活，知识综合性与交汇性强，一直是高考在交汇处命题的一大主阵地.而函数与方程思维、基本不等式思维、化归与转化思维等方法巧妙地把数列中的最值问题转化为函数的最值问题，因此利用函数方法或不等式方法来解决，可以拓广解题思维，同时数列本身的基本性质也为求解最值开辟了全新的思路.F