行星传动动态啮合有限元仿真分析

（西安科技大学 机械工程学院，西安 710054）

0 引言

行星轮系工作可靠，传动效率高，适用范围广，要保持平稳的齿轮啮合传动过程，有必要对齿轮进行强度分析。啮合是一种典型的接触问题。在若干假设前提下，传统的齿轮的接触强度计算不能准确反映啮合过程中的应力以及应变分布与变化。而齿轮在实际传动过程中两齿面的接触区域是不断发生变化的，采用有限元分析方法则可以准确、快速计算，直观方便的查看计算的接触应力分布等优点。

本文运用ABAQUS软件，基于经典赫兹接触理论，分别采用准静态分析方法与显示动力分析模拟行星齿轮传动中轮齿啮合情况，研究轮齿接触应力与齿根应力分布规律，对比两种方法与理论分析，可以为行星轮系设计提供更为可靠的设计保证。

1 传统理论应力分析

齿轮的失效形式主要是齿面损伤和轮齿折断。工作时，各个轮齿表面接触应力是按脉动循环变化的，若齿面最大接触应力大于材料的接触应力极限，则在多次重复载荷作用下，齿轮表面会逐渐产生细小的裂纹，裂纹慢慢扩展，甚至会形成疲劳点蚀，对传动的稳定性有很大的影响，伴随着产生振动和噪声，影响齿轮的正常工作，甚至会引起齿轮的破坏。另外，在行星齿轮传动中，当轮齿受到载荷的反复作用，齿根弯曲应力大于材料的弯曲应力极限时，齿根部分将产生疲劳裂纹，随着裂纹不断扩展，最终轮齿产生疲劳折断。基于这两种失效形式，故对齿轮的接触强度与齿根弯曲疲劳强度进行强度校核。

1.1 齿轮接触应力计算

两物体相互接触时，在接触区域附近会产生局部应力和局部变形，称为接触应力和接触变形，本文采用经典赫兹接触理论来进行齿轮的接触应力的计算，齿轮啮合时，可将齿廓啮合点的曲率半径视为接触圆柱体的半径，齿轮节点处一般只有一对齿啮合，节线附近的齿根表面往往先出现点蚀。因此接触疲劳强度计算通常以节点为计算点，可得接触应力公式：

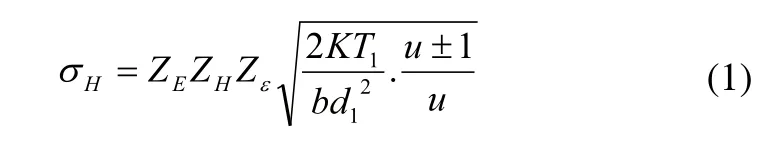
其中由机械手册中可查出：

K为载荷系数；

ZE为弹性系数；

ZH为节点区域系数；

Zε为重合度系数；

d1为小齿轮的分度圆直径；

u为大小齿轮齿数之比；

T1为主动轮的扭矩。

许用接触应力：

式中：σHlim为失效概率为1%时，试验齿轮的接触疲劳极限；

SHmin为接触强度的最小安全系数；

ZN为接触疲劳强度极限，均可由机械设计手册查出。

1.2 齿根弯曲疲劳强度计算

由于轮缘刚度很大，故将轮齿视为是具有一定宽度的悬臂梁。理论上载荷应由同时啮合的多对齿分担，为简化计算，通常假设载荷只作用于只有一对齿啮合时的齿顶进行分析，并采用重合度系数予以修正。在载荷长期作用下，轮齿齿根受拉一侧先产生疲劳裂纹，故齿根弯曲疲劳强度以受拉侧为计算依据。齿根弯曲强度校核公式：

单向受载时，许用弯曲应力公式：

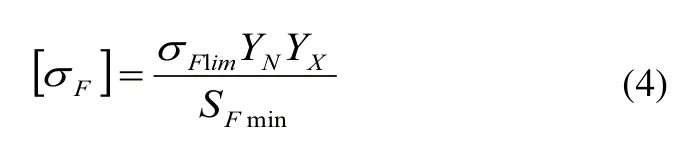
将中心轮、行星轮、内齿轮的各个相应参数代入式(1)～式(4)计算可得各齿轮的接触应力和弯曲应力。

2 有限元分析模型构建

太阳轮与行星齿轮的接触和行星齿轮与内齿轮的接触都存在相对运动的摩擦力，由于摩擦力相对正压力很小，所以在分析过程中设定摩擦系数。在有限元分析中，接触过程通常依赖于时间，且在接触界面上运动学和动力学的状态是事前未知的。本文主要是利用ABAQUS对行星齿轮传动机构进行齿轮啮合的接触分析，查看传动过程中齿面接触应力。

2.1 Abaqus有限元分析前处理

齿轮有限元分析属于结构分析，初始状态下模型的响应由线弹性模型确定，材料定义为各向同性，并通过输入弹性模量、泊松比、和质量密度三个物理量来完成材料属性定义。本文中心轮和行星轮均采用20CrMnTi，齿面硬度58～62HRC，渗碳淬火，加工精度6级。内齿圈均采用42CrMo，加工精度7级。材料属性如表1所示。

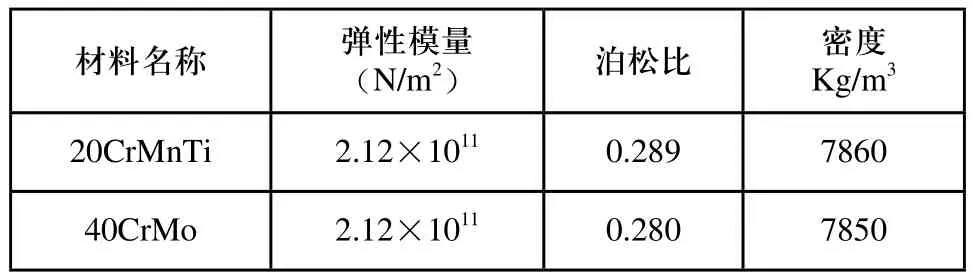
表1 材料属性表

网格划分是否合理影响分析结果精度，网格过疏结果误差较大，网格过密计算机工作量较大耗时长。由于行星轮结构较为复杂，本文简化模型分析单齿的啮合，在划分网格时采用结构化网格和局部网格细化技术，在接触面附近设置较密种子，既减少网格数量又减小了分析误差划分。网格单元类型为C3D8R，单元个数为，网格划分模型如下图所示。

根据行星轮传动机构的实际工况进行边界条件设置，约束内齿轮所有自由度，释放太阳轮绕轴线的旋转自由度，约束其他自由度，行星轮既可以绕其轴线旋转，又可以绕太阳轮旋转，因此释放切向位移和周向旋转位移。

2.2 准静态接触分析

ABAQUS/Standard采用Newton-Raphson算法求解非线性问题的，把分析过程划分为一系列的载荷增量步，在每个增量步内进行多次迭代，得到合理的解释后再求解下一个增量步，所有增量响应的总和就是非线性分析的近似解。

在齿轮接触分析前处理过程中，建立在接触关系初期直接施加力载荷，往往会导致分析计算不收敛，因此通过设置多个非线性静态通用步模拟行星轮系的动态分析，首先使用位移边界条件建立平稳接触，然后施加力载荷。

准静态模拟齿轮啮合传动仿真分析结果如下图所示，从分析云图中可以清楚地看到齿轮入啮到脱啮时接触应力大小位置与变化情况。随着齿轮副的进一步啮合，齿轮副在啮合点和齿根位置的应力较大，且太阳轮和行星轮啮合部分的齿面接触应力最大值为420.7 MPa，行星轮和内齿轮啮合部分的齿面接触应力最大为373.4MPa，应力云图如图1、图2所示。

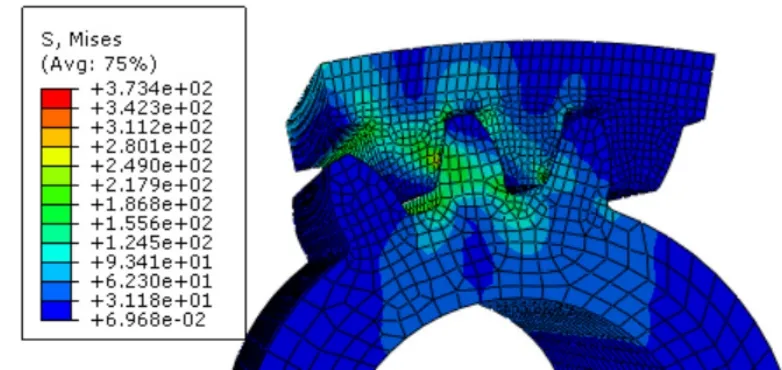
图1 内齿圈和行星轮啮合齿面接触应力

图2 太阳轮和行星轮啮合齿面接触应力

由于篇幅限制，在此仅列出0.14s、0.43s、0.71s 、1.00s时刻行星轮传动动态啮合情况，如图3～图6所示，由啮合云图可以看出，随着进一步啮入，太阳轮与行星轮齿面接触应力大于行星轮与内齿圈，且接触应力在轮齿接触点处最大，并向齿根扩散。

图3 0.14s啮合云图

图4 0.43s啮合云图

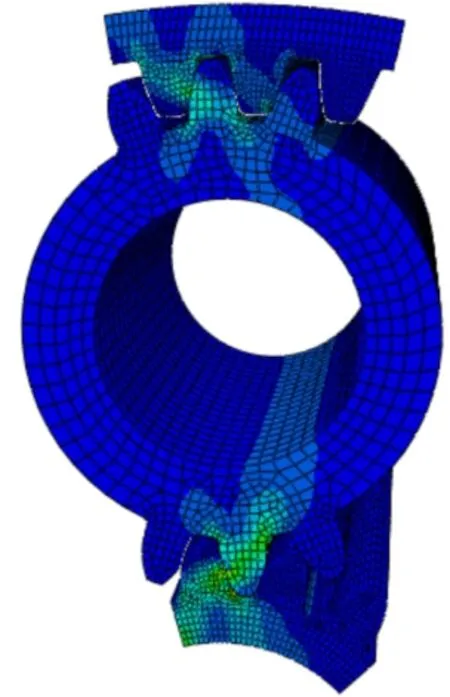
图5 0.71s啮合云图

图6 1.00s啮合云图

在ABAQUS中采用S-Max，Principle模块可以得到各齿轮的齿根弯曲应力大小及分布云图，其中内齿圈、行星轮、太阳轮的齿根弯曲应力云图如图7～图9所示。

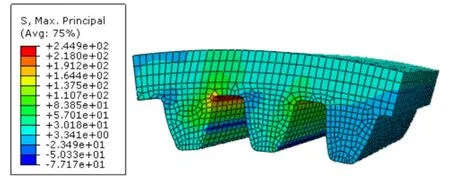
图7 内齿圈齿根弯曲应力云图

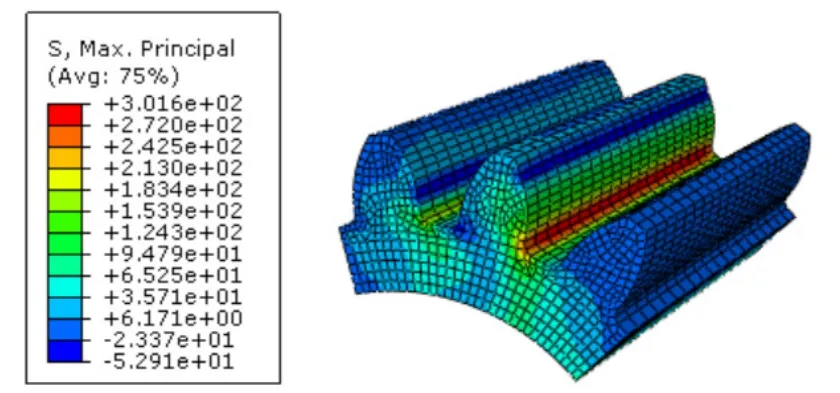
图8 太阳轮齿根弯曲应力云图

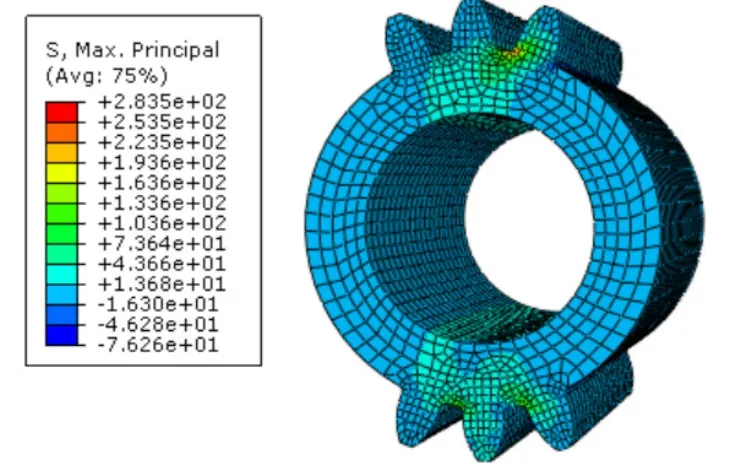
图9 行星轮齿根弯曲应力云图

从以上应力云图可以看出，内齿圈齿根弯曲应力244.9MPa，太阳轮齿根弯曲应力301.6MPa，行星轮齿根弯曲应力283.5MPa。均满足强度要求。

2.3 显示动力学分析

ABAQUS/Explicit在求解非线性问题时不需要进行迭代，而是显示地从上一个增量步的静力学状态来推算出动力学平衡方程的解。显示动力分析的求解过程需要大量的增量步，但由于不进行迭代，不需要求解全体方程组，并且每个增量步的计算成本很小，可以高效地解决复杂的非线性问题。

在进行齿轮模型接触分析时，ABAQUS会自动创建一个初始分析步来定义初始状态下的边界条件和相互作用，为使齿轮稳定接触，并能够仿真太阳轮的啮入和啮出过程，本文创建两个动态显式分析步，第一个分析步设为0.005s，第二个分析步设为0.06s，Nlgoem选择ON。为加速分析，降低计算成本，质量放大系数为10。质量放大倍数越大，计算速度越快，但同时也会使齿轮惯性增大，计算结果不够精确。本分析中应力云图如下所示，其中太阳轮和行星轮啮合部分的齿面接触应力最大值为473.8MPa，行星轮和内齿轮啮合部分的齿面接触应力最大为511.9MPa。

图10 内齿圈和行星轮啮合齿面接触应力

本分析同样列出0.14s、0.43s、0.71s、1.00s时刻行星轮传动动态啮合情况，如图3～图6所示，由啮合云图可以看出，在显示动力学分析下的轮齿啮合过程中，接触应力依旧在轮齿接触点处最大，并向齿根扩散。其中太阳轮与行星轮啮合处、行星轮与内齿圈啮合处均出现最大应力点。

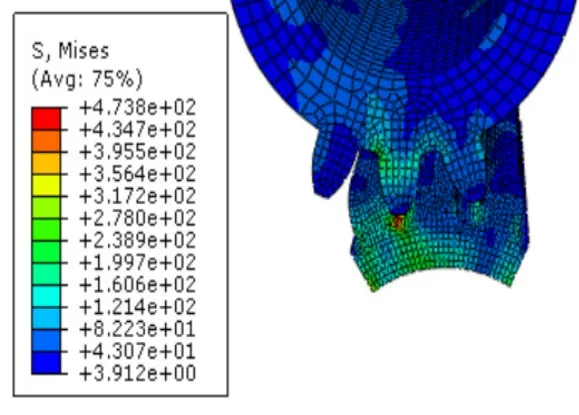
图11 太阳轮和行星轮啮合齿面接触应力

图12 0.14s啮合云图

图13 0.43s啮合云图

图14 0.71s啮合云图

图15 1.00s啮合云图

采用S-Max，Principle模块得到各齿轮的齿根弯曲应力大小及分布云图，其中内齿圈、行星轮、太阳轮的齿根弯曲应力云图如图7～图9所示。

图16 内齿圈齿根弯曲应力云图

图17 行星轮齿根弯曲应力云图

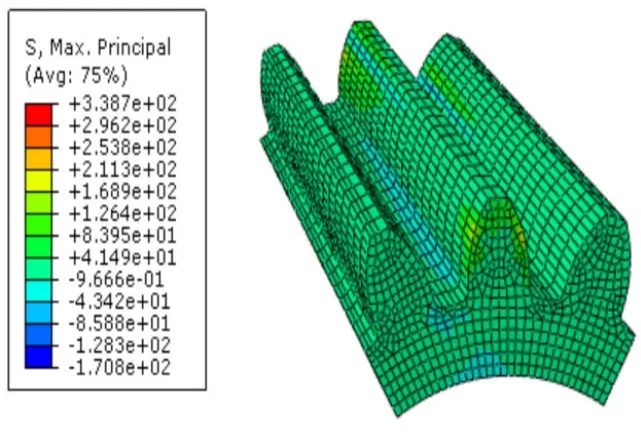
图18 太阳轮齿根弯曲应力云图

从齿根弯曲应力云图可以看出，啮合过程中内齿圈齿根弯曲应力286.8MPa，太阳轮齿根弯曲应力338.7 MPa，行星轮齿根弯曲应力265MPa。

2.4 两种仿真分析对比

按照标准渐开线圆柱直齿轮的强度校核方法，所得各个齿轮接触应力与齿根应力，仿真结果与理论值对比如表2所示。

表2 仿真结果与理论结果对比表

由上表对比可知，理论分析结果与两种仿真结果存在一定误差，这是由于理论分析时把接触看作线接触，而在分析软件中，模型采取面接触，较理论分析可进一步提高计算准确性。无论是采用准静态分析还是显示动力分析都可以求出了各个啮合轮齿处于不同啮合位置的接触压力、应力的大小及其分布。动态分析可以在一次求解过程中，计算不同啮合位置处的应力及其变化趋势。但是动态分析时，齿轮啮合状态会不断在单齿啮合与双齿啮合交替变换，在啮入啮出时会存在啮合冲击，使得齿轮产生较大冲击应力。使用显示动态分析得到的轮齿应力随时间变化的仿真结果会更加接近实际齿轮啮合过程。下图所示分别为单齿啮合时，准静态分析过程与显示动力分析过程中太阳轮应力沿齿根方向的变化云图。

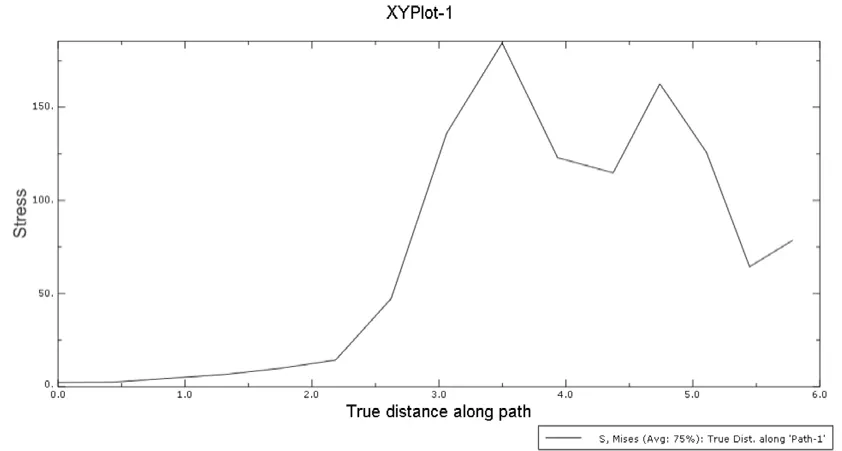
图19 准静态分析过程太阳轮接触应力沿齿根方向的变化云图

在上述云图中，可以看出静态分析在3.5处应力达到最大值，在4.5附近又出现较大应力处，而动力分析中啮合在4.5处出现应力峰值，而齿轮在啮合过程中，主动齿的应力由齿顶向齿根方向扩散，在节圆处达到最大值。

3 结论

本文主要对比了两种仿真分析方法对于行星传动动态啮合轮齿的应力分布规律，探究了齿轮在不同啮合位置时齿面的接触应力、齿根应力的变化等，结论与理论分析基本吻合。

准静态通用分析能够模拟行星轮系动态分析，建立较为平稳的接触关系，在分析中计算稍许简便。且仿真结果与理论值误差较小。显示动力分析能够高保真地模拟出齿轮实际啮合过程，对于进一步轮系的动态特性研究有着深刻意义。而在实际生产生活中，结合两种仿真方法与理论分析，则将对轮系的优化以及系统可靠性研究提供重要保证。