分组马尔可夫叠加传输在非高斯脉冲信道上的性能研究

2019-03-28马啸吉眉颖陈声晓

通信学报 2019年3期

马啸，吉眉颖，陈声晓

马啸1,3，吉眉颖1,3，陈声晓2,3

（1. 中山大学数据科学与计算机学院，广东广州 510006；2. 中山大学电子与信息工程学院，广东广州 510006；3. 中山大学广东省信息安全重点实验室，广东广州 510006；）

研究了非高斯脉冲信道上的分组马尔可夫叠加传输机制。基于精灵辅助等效系统，分析了分组马尔可夫叠加传输系统的性能下界。仿真结果表明，在特征因子不同的非高斯脉冲信道上，分组马尔可夫叠加编码技术均可获得较高的编码增益，且误比特率较低区域的误码性能均可与精灵辅助下界贴合。在BER = 10−5时，分组马可夫叠加传输系统便可达到距离香农限约0.85 dB的性能。

分组马尔可夫叠加传输；非高斯脉冲信道；SS信道模型；精灵辅助下界

1 引言

传统通信系统中的信道编码以及调制技术研究大多是基于加性高斯白噪声信道（AWGN，additive white Gaussian noise）模型的假设，然而在多数实际通信系统中这一假设并不总是成立的，如在电力线通信、水声通信等系统中由于电磁辐射叠加等原因产生脉冲噪声，而此类噪声分布一般是非高斯的[1]。为了进一步研究非高斯脉冲信道下的可靠通信系统，科研人员建立了多种描述该信道噪声分布的统计模型[2-3]，本文采用基于广义中心极限定理的对称稳态（SS，symmetric alpha stable）分布模型[2]。该模型在多个领域都得到了广泛应用，如信号处理、雷达通信等。

信道编码是保证通信系统可靠传输的关键技术。文献[4-8]分别研究了多种编码技术在非高斯脉冲信道条件下的性能。文献[4]提出了一种适用于该信道条件下的卷积码的维特比译码算法。文献[5]提出了非高斯脉冲噪声上Turbo均衡性能分析的改进外信息转移（EXIT，extrinsic information transfer）图方法。文献[6]则研究了Turbo网络编码调制（Turbo TCM, Turbo trellis-coded modulation）码在非高斯脉冲信道上的性能。文献[7]利用EXIT图方法研究了低密度单奇偶校验（LDPC，low-density parity-check）码的设计方案，而文献[8]则提出了联合信道估计和LDPC译码的方案。通常情况下，编码系统的误码性能可以通过蒙特卡洛仿真来获知。此外，信道容量通常也被作为衡量传输方案性能的标准。文献[9]中分析了采用SS信道模型时通信系统的信道容量，并给出了不同关键参数对于系统信道容量的影响。

当通信系统选取的信道编码方案的纠错能力较差时，传统的方案采用将编码后的码字重复传输的方法来进一步降低误码率，不过，重复传输会造成严重的码率损失和功率损耗，大大降低传输效率。本文提出在非高斯脉冲信道下采用分组马尔可夫叠加传输[10]（BMST，block Markov superposition transmission）方案来提高可靠性，该算法几乎不会带来码率损失。BMST编码可视为一类空间耦合码[11]，信息序列先通过基本码（basic code）进行编码，然后将编码后的序列进行交织，最后将交织后的序列进行分组马尔可夫叠加，从而达到既能重复传输多次又能保证传输效率的目的。BMST编码技术在AWGN信道[11]、湍流信道[12]下均有逼近香农限的能力和能够预测误码性能的下界，且在硬件资源允许的条件下，编码速度可以与基本码保持相近。BMST编码技术具有诸多优点，但是目前尚无相关工作研究其在非高斯脉冲信道上的性能。

本文将研究分组马尔可夫传输在非高斯脉冲信道上的性能，并通过其精灵辅助（GA，genie-aided）等效系统来分析BMST系统的性能下界。在仿真实验中，令卷积码为BMST的基本码，分析了BMST系统在非高斯脉冲信道下的误码性能，并验证了不同参数条件下的仿真结果均可与GA性能下界贴合，以及BMST系统在该信道下具有逼近香农限的能力。

2 系统模型

2.1 系统设置

本文考虑一个非高斯脉冲信道下的系统模型，该系统包含3个基本单元，分别是发送设备、非高斯脉冲信道和接收设备。在发送端，信源发出的信息通过BMST编码器进行编码，并采用二进制相移键控（BPSK，binary phase shift keying）方式进行调制。在接收端，接收信号序列可以表示为

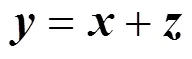
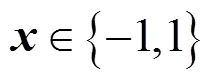
2.2 噪声模型

本文的噪声模型将采用SS分布模型。SS模型是一个零均值的稳态分布模型[2]，SS分布模型的概率密度函数如式(2)所示。

其中，α为特征因子，决定了分布的拖尾程度，α值越小，概率密度函数的尾部越“厚”，图1表示了不同α值下的SαS分布概率密度函数；γ为分散系数，γ > 0，描述样本偏离分布均值的程度；δ为均值，它的大小取决于α的值。SαS分布模型有以下2种特殊情况：1) 当α = 2时，该分布是高斯分布，其方差是有限的且等于2γ ；2) 当α = 1时，该分布是柯西分布。由于大多数实际环境中噪声的α值范围为1~2，因此本文设置。

由于求解式(2)的积分复杂度很高，本文在仿真实验中采用查表法来降低计算复杂度。

2.3 几何信噪比

因为SS随机变量二阶矩是不存在的，所以当小于的阶矩存在时，用分数低阶矩（FLOM, fractional lower order moments）来描述脉冲信号的特征，如式(3)所示。

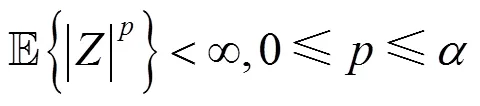
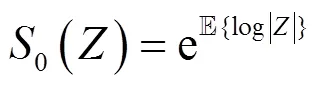
由式(4)可得SS过程的几何功率的封闭表达式为

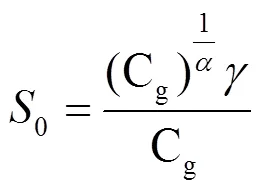
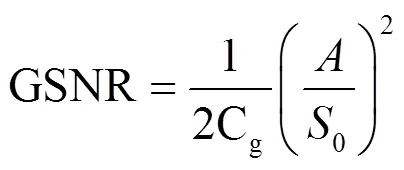
其中，表示码率。

2.4 互信息分析

互信息分析是编码调制研究中的一种重要的分析方法。一般地，在给定系统模型、信道情况下，可以通过互信息的计算来获得该编码系统可以达到的最大传输速率，进而得到达到某一特定信息传输速率所需的最小信噪比（SNR，signal to noise ratio），即香农（Shannon）限。根据香农限可以分析和对比该系统所用的信道编码方案的性能表现，并得知该编码调制系统在传输可靠性上还有多大的优化空间。本文的系统模型已由式(1)给出，假设发射信号和接收信号对应的随机变量别为和，则信道输入信号和信道输出信号之间的互信息为

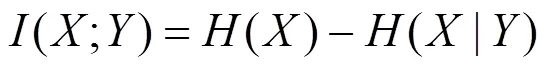
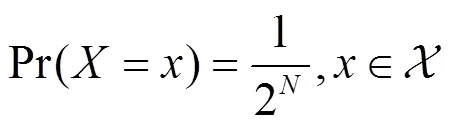
进而可以求得

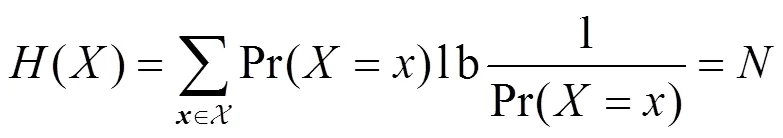
此外

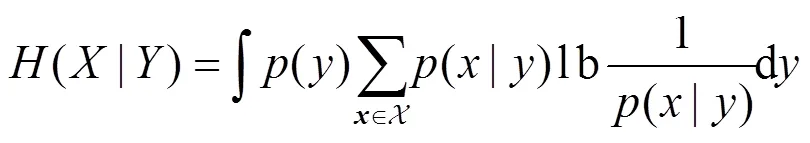
而在实际计算中可以用蒙特卡洛仿真求解式(11)的积分。

3 BMST编译码算法

3.1 BMST编码

一个记忆长度为的分组马尔可夫传输的编码调制过程如图2所示。该编码系统是由一个基本码编码器、+1个交织器和BPSK调制器组成的。

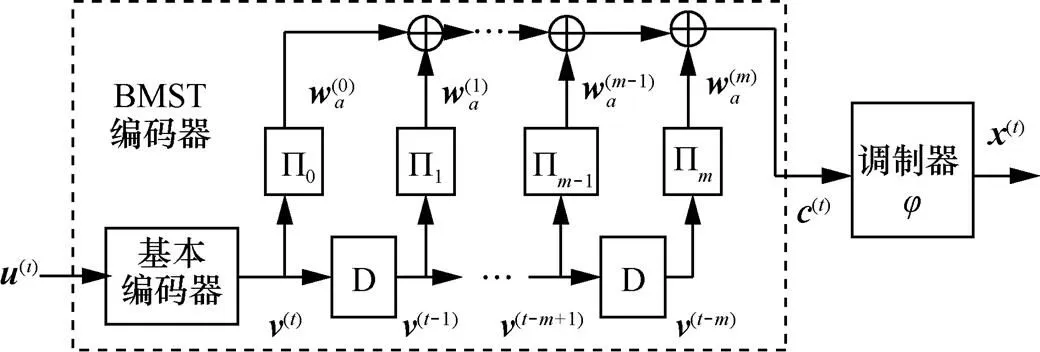
图2 记忆长度为m的BMST编码调制框架

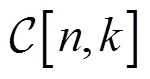
算法1 BMST系统的编码调制算法

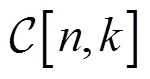
4) 调制。用BPSK调制将(t)调制成(t)。

3.2 译码算法

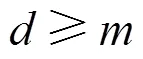
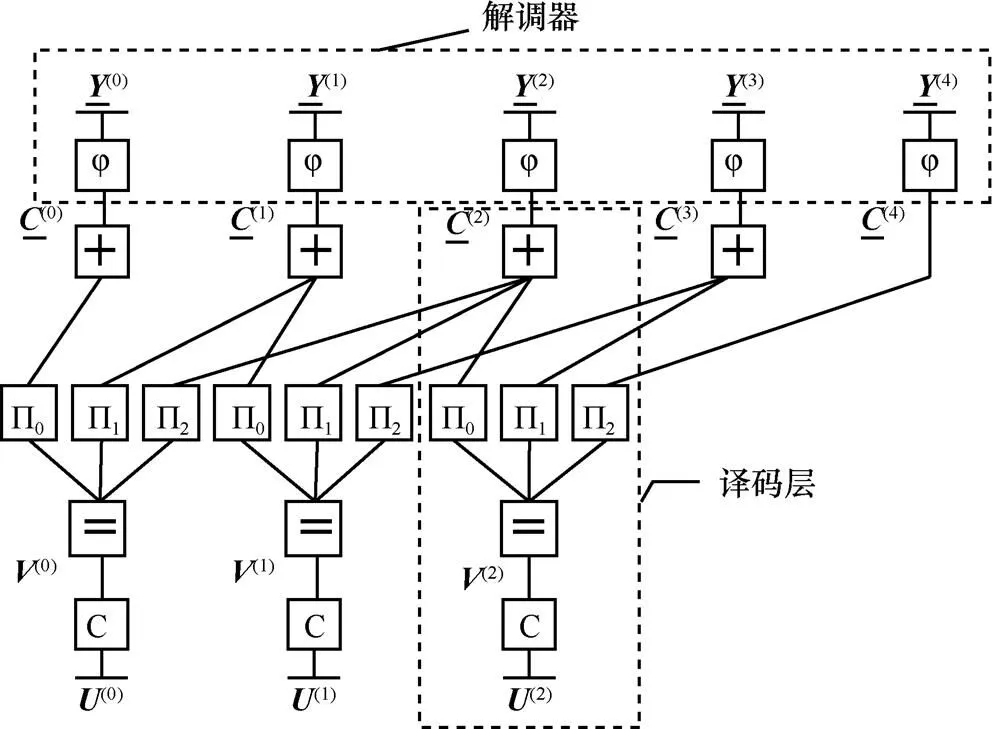
图3 L = 3，m = 2的BMST译码正规图

算法2 BMST系统的迭代滑窗解调译码算法

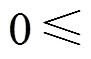
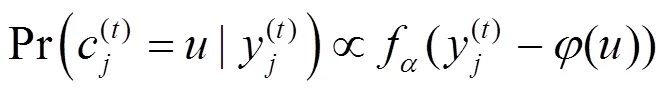
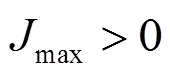
3.3 精灵辅助下界

本节分析得到BMST系统在非高斯脉冲信道上的精灵辅助下界。文献[10]中给出了BMST基本码为线性二元码，调制方式为BPSK，在加性高斯白噪声信道下的GA性能下界如式(13)所示。

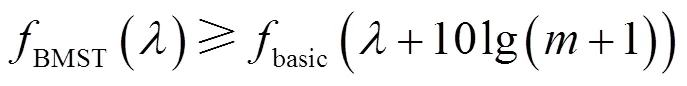
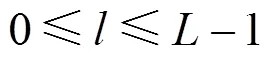
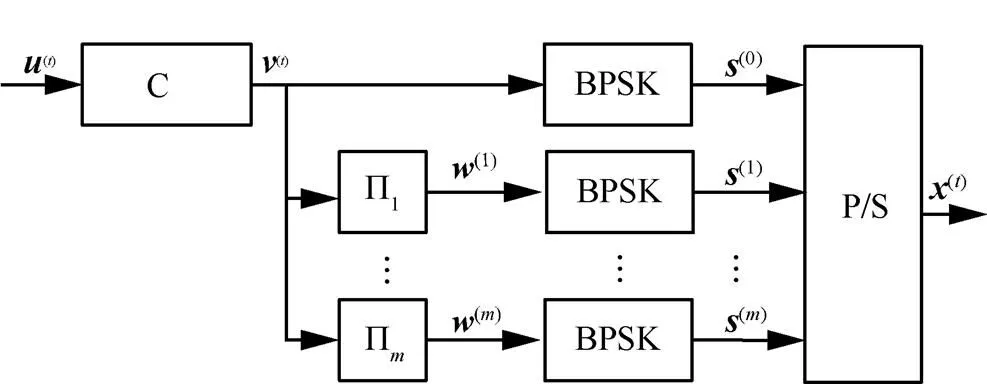
图4 GA译码等效系统框架

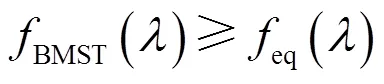
4 复杂度分析

5 数值结果

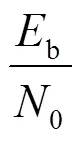
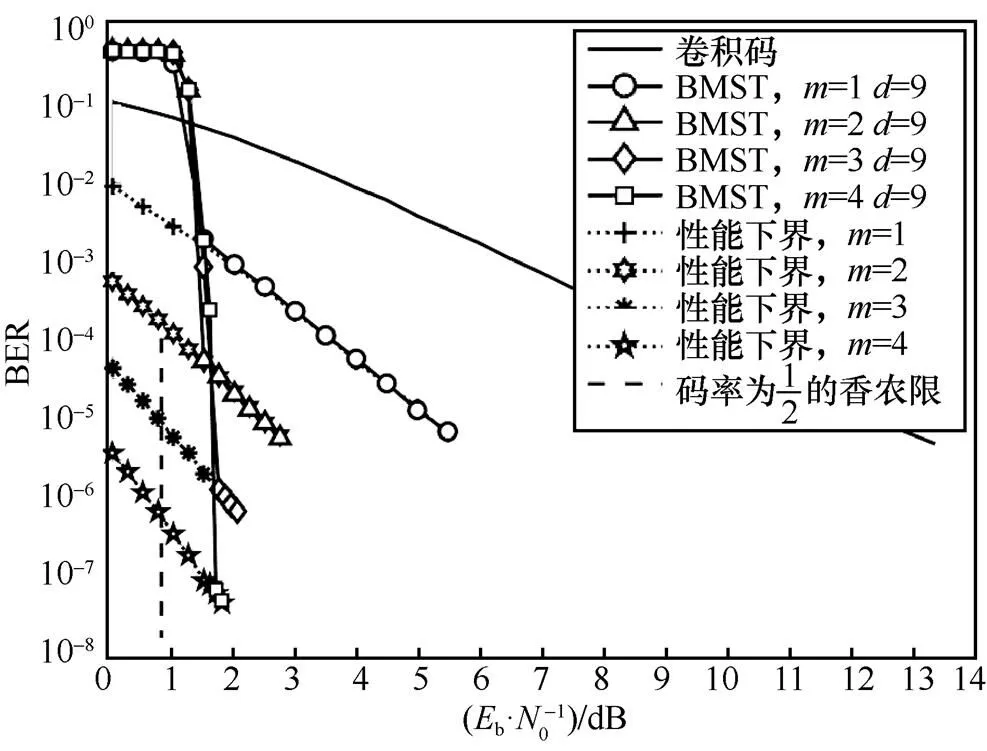
图5 非高斯脉冲信道上BMST系统在不同记忆长度m下的仿真性能曲线

例2 图6 给出了在特征因子= 1.5的非高斯脉冲信道上BMST、LDPC码、卷积码这3种编码方案性能比较。由仿真结果可知，与卷积码相比，BMST编码与LDPC码均具有良好的性能。记忆长度=2的BMST编码方案在瀑布区性能优于LDPC码，但LDPC码具有更低的错误平层。不过，= 3的BMST编码方案的误码性能是远远好于LDPC码的。因此，BMST编码方案在记忆长度较大的情况下的性能是可以赶超LDPC码的。此外，与卷积码、LDPC码相比，BMST编码方案可以通过GA等效系统来预测性能下界。

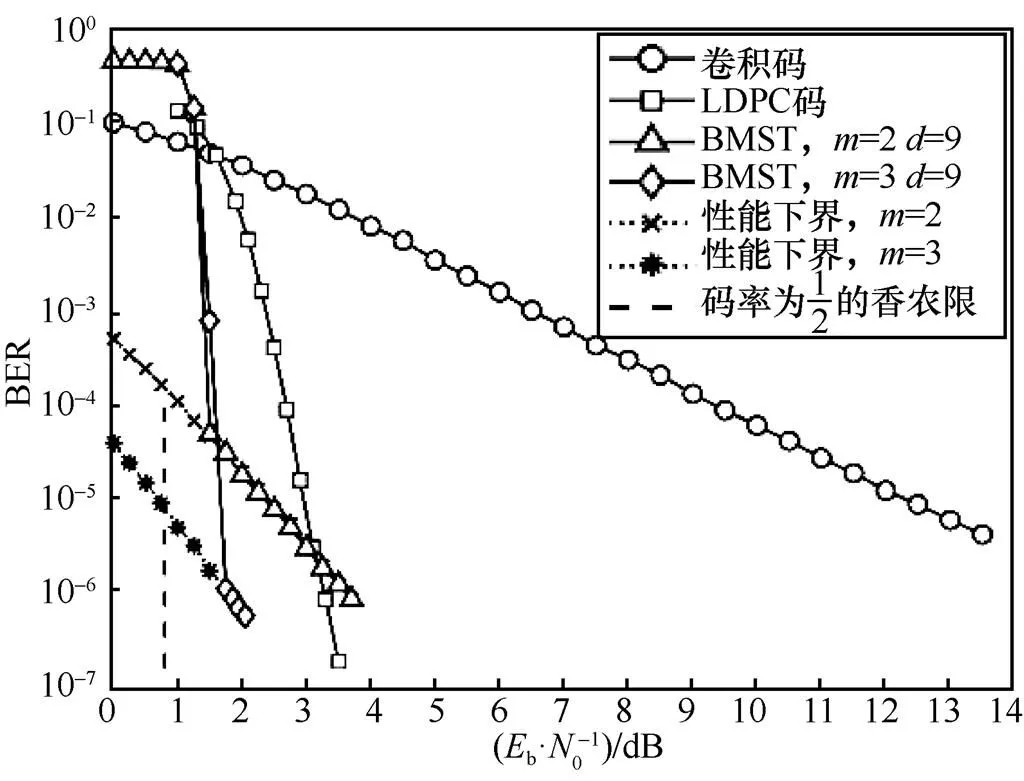
图6 非高斯脉冲信道上卷积码、LDPC码与BMST编码的仿真性能比较

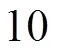
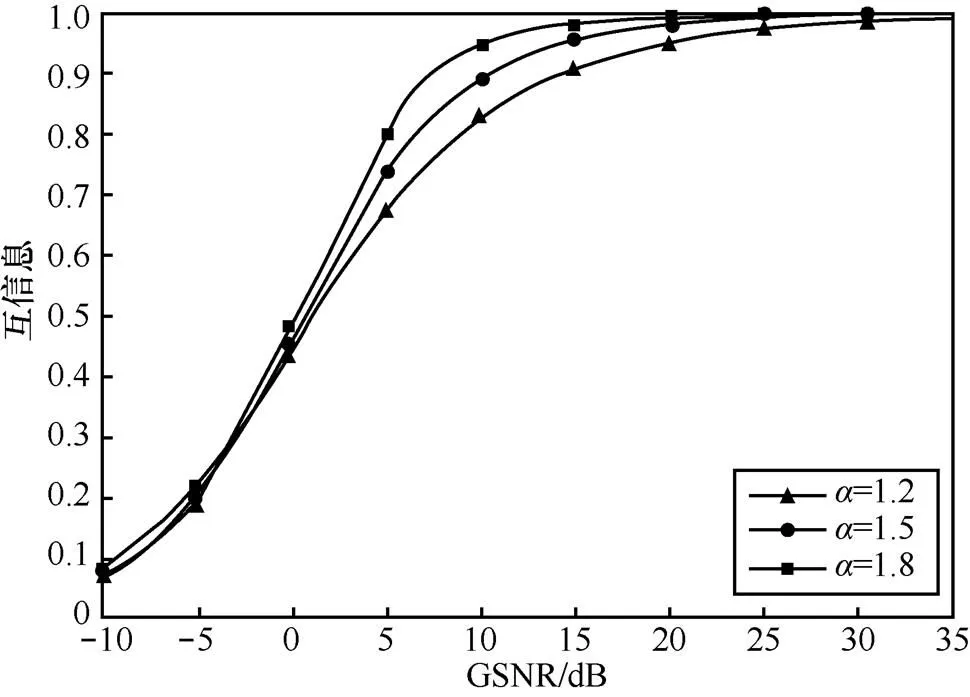
图7 α =1.2、1.5、1.8的非高斯脉冲信道的互信息性能曲线

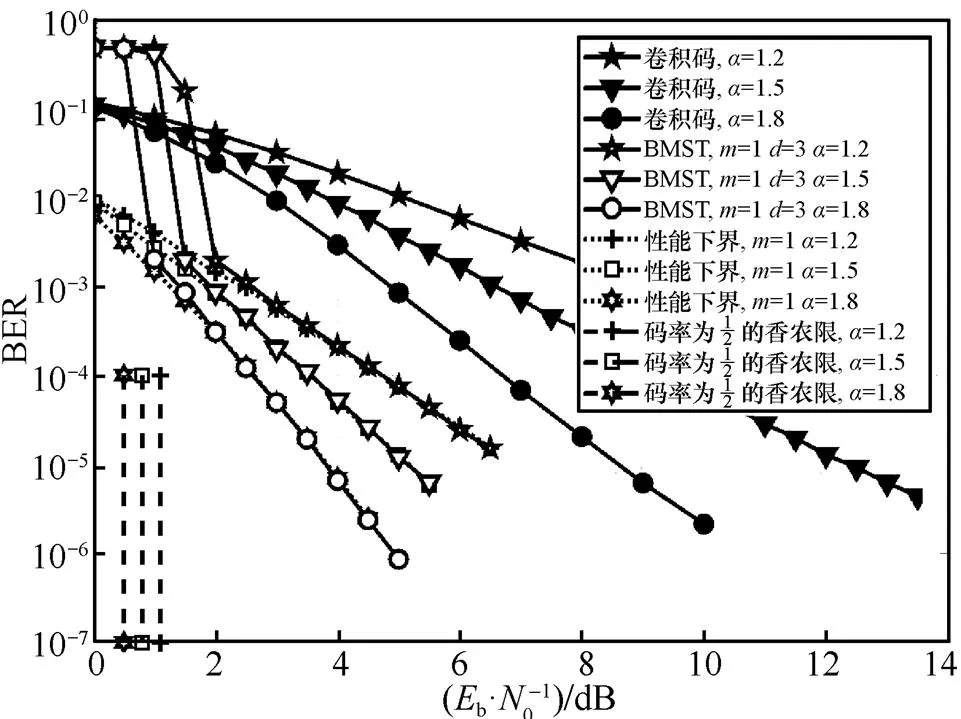
图8 α =1.2、1.5、1.8的非高斯脉冲信道上BMST系统的仿真性能曲线

6 结束语

本文研究了非高斯脉冲信道下分组马尔可夫叠加传输的性能，并基于GA等效系统分析了系统的性能下界。数值仿真结果表明，BMST系统在不同特征因子的非高斯脉冲信道下均能有效工作，并且其性能增益随着记忆长度的增大而增大。特别地，在误比特率较低的区域中，BMST迭代滑窗解调/译码算法的误码性能（即仿真实验所得的BER性能曲线）均能与GA性能下界贴合。

BMST系统可以通过选取码率可变的基本码来实现码率灵活可调，例如，在BMST系统中采用重复码和单奇偶校验码的笛卡尔积作为基本码，便可实现任意码率，能够在AWGN信道下逼近信道容量，且具有可预测并容易求得的性能下界，该下界可以为BMST系统编译码的参数选择提供参考[12,17]。下一步将研究非高斯脉冲信道下的码率可调的BMST系统，实现给定信噪比约束条件下的可靠通信。

[1] MEI Z, CHEN L. Density evolution analysis of LDPC codes with different receivers on impulsive noise channels[C]//2015 IEEE/CIC International Conference on Communications in China (ICCC). 2015: 2-4.

[2] NIKIAS C L, SHAO M. Signal processing with alpha-stable distributions and applications[M]. Wiley-Interscience, 1995.

[3] NOLAN J P. Numerical calculation of stable densities and distribution functions[J]. Communications in Statistics. Stochastic Models, 1997, 13(4): 759-774.

[4] CHITRE M A, POTTER J R, ONG S H. Viterbi decoding of convolutional codes in symmetric α-stable noise[J]. IEEE Transactions on Communications, 2007, 55(12): 2230-2233.

[5] 罗康生, 赵明生. 非高斯脉冲噪声下Turbo均衡性能分析的改进 EXIT 图方法[J]. 电子与信息学报, 2009, 31(6): 1386-1389. LUO K, ZHAO M. Modified EXIT chart method for performance analysis of Turbo equalization in non-Gaussian impulsive noise environments[J]. Journal of Electronics Information Technology, 2009, 31(6): 1386-1389.

[6] KOIKE K, OGIWARA H. Application of Turbo TCM codes for impulsive noise channel[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 1998, 81(10): 2032-2039.

[7] DAI B, LIU R, HOU Y, et al. EXIT chart aided LDPC code design for symmetric alpha-stable impulsive noise[J]. IEEE Communications Letters, 2017, 21(3): 464-467.

[8] HOU Y, LIU R, DAI B, et al. Joint channel estimation and LDPC decoding over time-varying impulsive noise channels[J]. IEEE Transactions on Communications, 2018, 66(6): 2376-2383.

[9] WANG J, KURUOGLU E E, ZHOU T. Alpha-stable channel capacity[J]. IEEE Communications Letters, 2011, 15(10): 1107-1109.

[10] MA X, LIANG C, HUANG K, et al. Block Markov superposition transmission: construction of big convolutional codes from shortcodes[J]. IEEE Transactions on Information Theory, 2015, 61(6): 3150-3163.

[11] HUANG K, MA X. Performance analysis of block Markov superposition transmission of short codes[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(2):362-374.

[12] 朱锦顺, 马啸. 户外无线光通信中湍流信道下的分组马尔可夫叠加传输研究[J]. 通信学报, 2017, 38(7): 131-140. ZHU J, MA X. Block Markov superposition transmission over turbulence channels in outdoor optical wireless communications[J]. Journal on Communications, 2017, 38(7):131-140.

[13] GONZALEZ J G, PAREDES J L, ARCE G R. Zero-order statistics: a mathematical framework for the processing and characterization of very impulsive signals[J]. IEEE Transactions on Signal Processing, 2006, 54(10): 3839-3851.

[14] MA X, LIANG C, HUANG K. Obtaining extra coding gain for short codes by block Markov superposition transmission[C]//2013 IEEE International Symposium on Information Theory. 2013: 2054-2058.

[15] FORNEY G D. Codes on graphs: Normal realizations[J]. IEEE Transactions on Information Theory, 2001, 47(2):520-548.

[16] BAHL L, COCKE J, JELINEK F, et al. Optimal decoding of linear codes for minimizing symbol error rate[J]. IEEE Transactions on Information Theory, 1974, 20(2): 284-287.

[17] HU J, MA X, LIANG C. Block Markov superposition transmission of repetition and single-parity-check codes[J]. IEEE Communications Letters, 2015, 19(2): 131-134.

Performance of block Markov superposition transmission over non-Gaussian impulsive channels

MA Xiao1,3, JI Meiying1,3, CHEN Shengxiao2,3

1. School of Data and Computer Science, Sun Yat-sen University, Guangzhou 510006, China 2. School of Electronics and Information Technology, Sun Yat-sen University, Guangzhou 510006, China 3. Guangdong Key Laboratory of Information Security Technology, Sun Yat-sen University, Guangzhou 510006, China

Block Markov superposition transmission scheme was used over channels with symmetric alpha-stable (SS) impulsive noise. Based on the equivalent genie-aided system, the lower bound of the block Markov superposition transmission system was analyzed. Numerical simulations over non-Gaussian impulsive channels with different characteristic exponents show that, in the low bit-error rate region, performance of the block Markov superposition transmission system matches well with the lower bound. Block Markov superposition transmission scheme performs well (with 0.85 dB away from Shannon limits at the BER of 10−5) over non-Gaussian impulsive channels.

block Markov superposition transmission (BMST), non-Gaussian impulsive channel, symmetric alpha-stable (SS) model, genie-aided lower bound

TN911.22

10.11959/j.issn.1000−436x.2019046

2018−04−16；

2018−11−29

国家自然科学基金资助项目（No.91438101, No.61771499）；广东省自然科学基金重大基础研究培育基金资助项目（No.2016A030308008）；中山大学高校基本科研业务费2017年度重大项目和前沿新兴交叉学科培育资助计划基金资助项目（No.17lgjc22, No.17lgjc45）

The National Natural Science Foundation of China (No.91438101, No.61771499),The Basic Research Project of Guangdong Provincial NSF (No.2016A030308008), The Fundamental Research Funds for the Central Universities (No.17lgjc22, No.17lgjc45)

马啸（1968– ），男，河南焦作人，博士，中山大学教授、博士生导师，主要研究方向为信息与编码理论、编码调制技术、无线通信、光通信等。