基于ARIMA和EEMD的东江流域季节降水预报研究

，，

(1.广东省东江流域管理局，广东惠州516003；2.长江水利委员会水文局荆江水文水资源勘测局，湖北荆州434000；3.中山大学地理科学与规划学院，广东广州510275)

东江是珠江流域的重要组成支流，对广东省社会、经济发展具有十分重要的作用。它承担着深圳、东莞、河源、惠州、广州东部地区以及香港等地共3 000多万人的供水任务[1]，同时具有防洪、发电、航运、压咸等多种功能。东江流域水量调度是合理配置水资源、保证这些功能实现的重要举措。而长期降水预报则为制定东江流域水量调度计划提供基础，降水预报的精度将极大地影响到这些计划制定的科学性、合理性和有效性，但目前东江流域在长期降水预报方面的研究还未有效地开展。因此，对东江流域建立科学有效的降水预报模型，将会为东江流域水资源管理提供有益参考和科学支撑。

长期降水预报的传统方法是统计方法[2-3]。随着计算机技术的发展和新的数学方法的涌现，很多的智能方法被水文工作者应用到长期水文预报中[4-5]，如BP神经网络法等，并取得了较好的效果。然而，这些现代方法通常要求识别影响长期降水的前期气象因子，而影响不同区域的前期气象因子不同，建模需要针对研究区域做大量的分析工作，限制了这些方法的实际应用。相比智能方法，统计方法(比如求和自回归移动平均时间序列分析法、ARIMA)不需要这些分析工作，更易于用于实际生产。但传统的统计方法把包含在降水中不同频率的信号看作一个综合体来处理，往往会对预测结果产生不利的影响。最近发展起来的EEMD(集合经验模态分解)方法能够将原始信号进行逐级分解并提取出其在不同尺度的局部特征信号，从而准确反映出原时间序列信号的物理特性。因此，将EEMD与ARIMA模型结合起来，能够充分利用各自的优点，在“分解—预测—重构”的构架下实现建模容易操作与预报精度提高的双重目的[6]。为验证EEMD与ARIMA结合的优越性，本文采用ARIMA及EEMD-ARIMA模型对东江流域季节性降水预报进行对比研究。

1 数据

1.1 东江流域概况

东江是珠江的一级支流，干流全长562 km，其中在江西省境内长度127 km，广东省境内435 km，平均坡降为0.35‰。东江流域总面积35 340 km2，其中广东省境内31 840 km2，占流域总面积的90%。东江流域属亚热带季风湿润气候区，多年平均年降水量在1 500～2 400 mm之间，具有明显的干湿季节，汛期降水(4—9月)占全年80%以上。降水空间分布上，西南多，东北少[7]。

1.2 站点降水数据

本文所研究的范围是东江流域控制站博罗水文站以上区域，所采用的实测降水数据为东江流域73个测站点1980—2015年的日降水，经累加计算得到各站点的月降水量并进一步整理为汛期、枯水期以及年的季节降水量供研究分析使用。73个降水测站点较为均匀地分布在东江流域的上下游及支流，具有较好的代表性。日降水记录在使用前，经过了严格的检查、剔除错误，能保证数据资料的可靠性和一致性。降水测站的位置分布见图1。

图1 东江流域及站点分布

为降水预报模型建立的需要，将降水观测数据分为率定和验证2个时期。由于测站降水资料的起始时间不完全相同(多数站点从1980年开始观测，少数站点从1985年开始观测)，因此，统一选定该研究区降水数据1985—2010年为建模的率定期，2011—2015年为建模的验证期，以便于统一比较不同方法所建立模型在率定期及验证期的预测效果。且本文所表述的汛期代表该年4—9月降水量，枯水期为10月至次年3月降水量，年代表水文年(东江流域一般指4月至次年3月)即每年汛期开始到次年枯水期结束期间的降水量。

2 方法

本文尝试2种预报方法：一种是自回归求和滑动平均(Auto Regressive and Moving Average Model，ARIMA)，另外一种是耦合集合经验模态分解(Ensemble Empirical Mode Decomposition ，EEMD)与ARIMA。

2.1 ARIMA建模方法

Box 和Jenkins 1977 年首次提出了自回归求和滑动平均过程(Auto Regressive and Moving Average Model)时间序列预测分析方法[8]，简称ARIMA(p，d，q)，其中，p为自回归项数，q为滑动平均项数，d为使之成为平稳序列的差分次数(阶数)。一般通过以下4个步骤建立 ARIMA 模型[9]。

a) 平稳性检验。通过时间序列的散点图或折线图对序列进行初步的平稳性判断。对非平稳的时间序列，则需对数据进行差分处理直至成为平稳序列。本文使用MATLAB软件工具中 adftest 语句进行平稳性检验。

b) 模型识别。由样本数据的自相关函数和偏自相关函数来确定模型的阶数p、q。

(3)

当给定序列差分至平稳序列后，选取不同的p、q及ARMA(p，q)模型参数，对{Xt}进行拟合，利用上式计算该模型相应的AIC值。改变模型的阶数及参数使式(3)达到极小的模型，认为是最佳模型。

d) 模型预测。模型预测根据模型的参数定阶的结果，确定最终的方程模型。本文使用 MATLAB 软件工具中的predict语句或其他预测功能对模型进行预测，以得到原始时间序列未来的预测数据。

本文ARIMA模型选择率定期为1985—2010年东江流域年、汛期、枯水期降水数据，验证期为2011—2015年东江流域年、汛期、枯水期降水数据。ARIMA建模可用图2表示。

2.2 EEMD-ARIMA建模方法

EEMD (Ensemble Empirical Mode Decomposition，集合经验模态分解)是针对非平稳、非线性数据处理的工具，现在应用很广泛[10]。EEMD概括地讲就是在原信号中加入若干次白噪声，再分别进行 EMD 处理，最后求平均的一种全局化方法其算法步骤如下[11]。

图2 ARIMA建模流程

Step1往目标数据X(t)中加入白噪声序列ωi(t)，其中X(t)为固定序列，ωi(t)为随机过程。对于第i次试验，构成的信噪混合体结果为：

Xi(t)=X(t)+ωi(t)

(4)

Step2进行EMD分解，分解成IMF的组合：

(5)

Step3重复Step1和Step2一定次数，加入的白噪声服从同一分布但每次又均不相同；

Step4对所有的IMF组合相对应的IMF求平均：

(6)

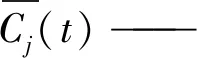
(7)

利用MATLAB，在ARIMA模型的基础上得到一个较为精确的预测，尝试将ARIMA与EEMD结合为新的预测方法EEMD-ARIMA，以提高东江流域季节降水预报的能力。EEMD-ARIMA模型的建立主要分为以下步骤。

a) EEMD数据处理。以东江流域年降水数据处理为例。将率定期内东江流域年降水数据进行EEMD处理，原始序列分解为从高频到低频的IMF1、IMF2、IMF3三个IMF分量及残差量，残差量即趋势项，记为IMF4，汛期数据分解记为IMF1_x、IMF2_x、IMF3_x、IMF4_x，枯水期记为IMF1_k、IMF2_k、IMF3_k、IMF4_k。

b) ARIMA模型建立。EEMD-ARIMA模型的建立(以东江流域年降水为例)见图3。

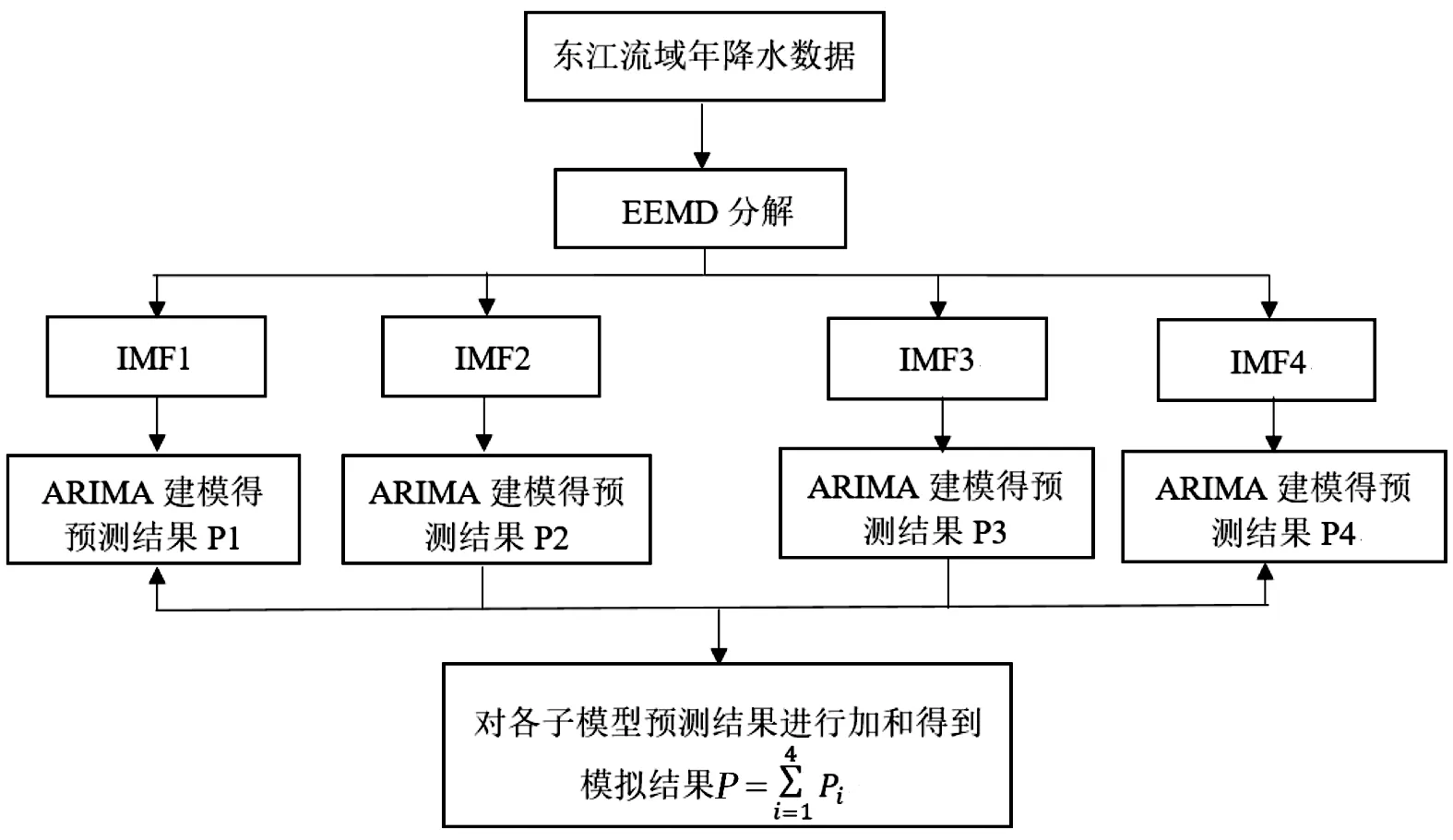
图3 EEMD-ARIMA模型建立流程

2.3 评价指标

为了能够评价各种预报模型的优劣，本文采用5项统计指标对不同的东江流域季节降水预报模型的预测效果进行评估，分别为平均绝对百分比误差(mean absolute percentage error,MAPE)、标准相对均方根误差(normalized root mean square error,NRMSE)、相关系数(R)及相对误差(relative bias，RB)在20%和40%以内比例。定义如下：

(8)

(9)

(10)

(11)

(12)

3 结果与分析

3.1 ARIMA模型结果与分析

由上述ARIMA建模步骤进行模型建立。将东江流域年、汛期、枯水期降水数据分别进行ARIMA建模，即确定各分量满足AIC极小值准则的p、d、q值。东江流域年降水、汛期、枯水期降水数据各分量建模结果见表1。

表1 东江流域ARIMA建模结果

结合2.3所提到的模型评价指标，东江流域汛期、枯水期及年降水序列ARIMA模型评价结果见表2，模型在率定期及验证期内的预测值与实测值的对比情况分别见图4、5。

表2 ARIMA模型预测结果评价

注：RB20%、RB40%分别指相对误差RB在20%以内、40%以内的比例。下同

由表2、图4可知，各降水预报模型率定期内都具有一定的预测效果，表现为MAPE和NRMSE均相对较低，预测相对误差值整体较低。其中，年降水预报模型的预测精度最佳，其MAPE、NRMSE分别为0.12、0.07，均为模型中最低，且预测值与实测值相对误差在20%以内比例(0.72)和40%以内的比例(1)均为最高，表明模型具有较高的预测精度；枯水期降水预报模型的MAPE(0.20)、NRMSE(0.62)均为最大，且相对误差在20%以内比例(0.46)和40%以内的比例(0.92)均为最低，表明模型的预测效果相对较差。另外由表可看出，枯水期的预测值与实测值的相关系数(0.75)是各模型中最高的，表明预测值的变化趋势与实测值最为接近，但在大部分年的相对误差较大，导致整体的预测结果相对最差。整体而言，ARIMA模型在率定期表现出了一定的预报能力。

由表2、图5可知，各降水预报模型验证期预测效果相比于率定期均表现出明显的下降趋势。其中，年降水预报模型验证期预测效果相比于率定期下降程度相对较小，预测效果在3种模型中相对最佳，其MAPE(0.15)和NRMSE(0.21)均为最小，预测值与实测值相对误差在20%以内比例(0.46)和40%以内的比例(0.58)均为最高；枯水期降水预报模型的预测效果整体而言下降趋势最为明显，其各项指标都明显低于率定期，模型预测值与实测值相对误差在20%以内比例(0.20)和40%以内的比例(0.40)均较低，表明模型在对大部分年的降水估计存在显著高估，导致模型的整体预测精度相对较低。整体而言，验证期内由于原始降水数据存在非线性、非平稳性的问题使建模过程中对序列信息捕捉不完整从而导致验证期时模型表现出了明显的下降趋势。

a) 汛期降水

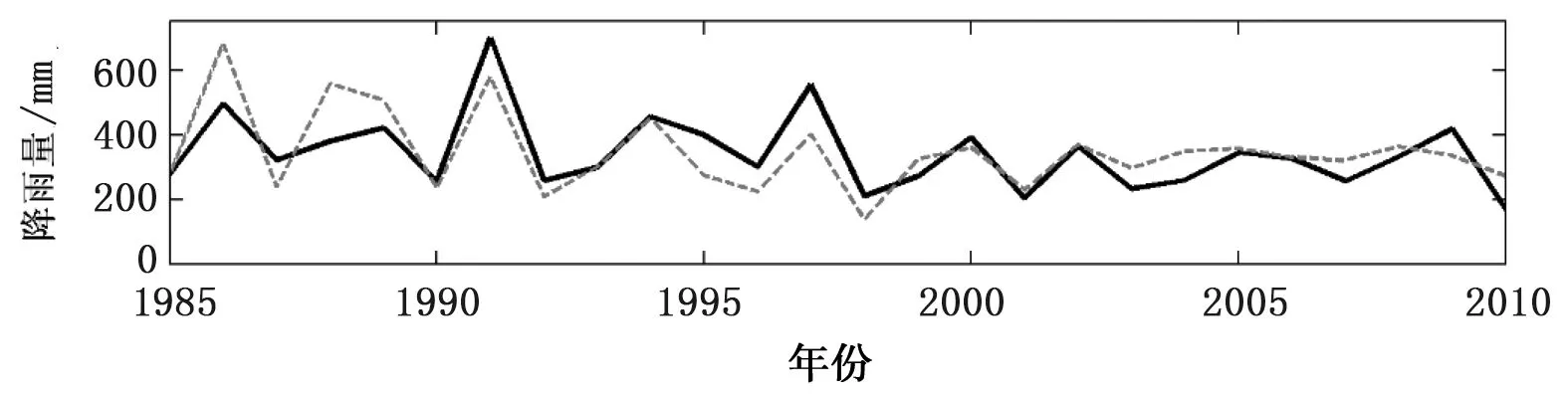
b) 枯水期降水

图4 ARIMA模型率定期内东江流域各降水预报模型预测值与实测值对比

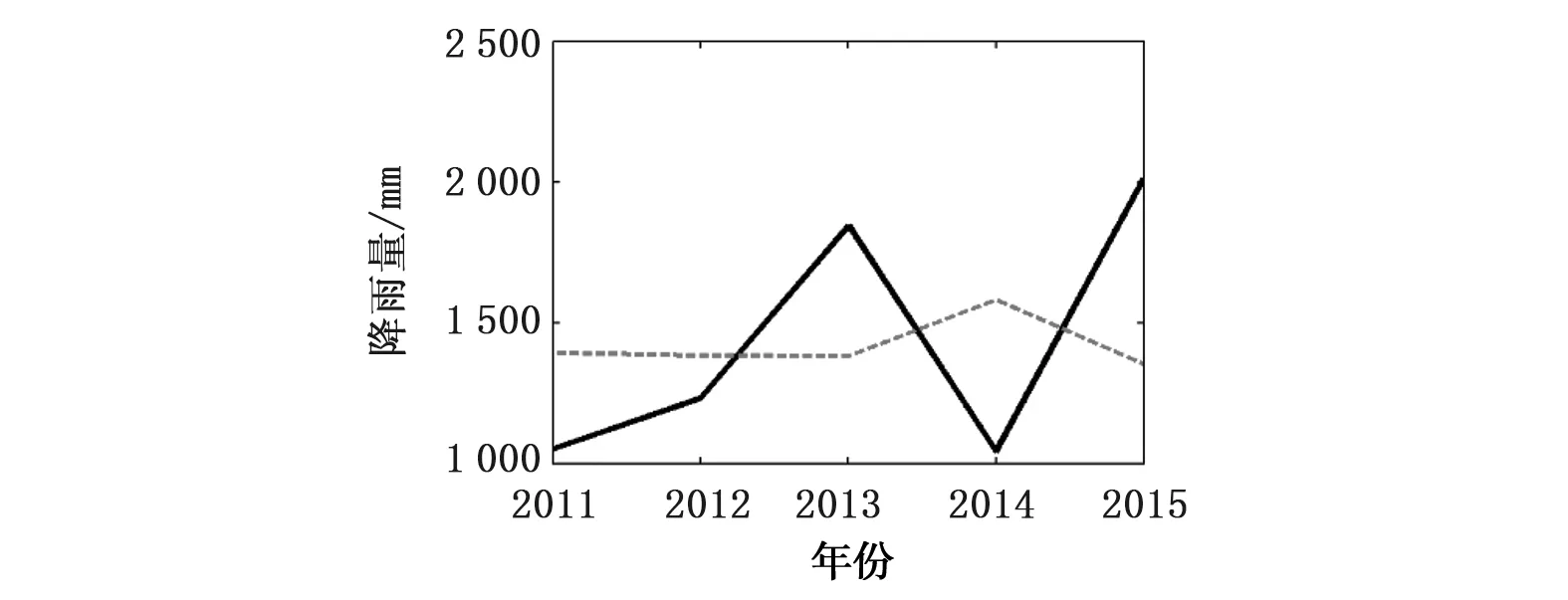
a) 汛期降水

b) 枯水期降水

图5 ARIMA模型验证期内东江流域各降水预报模型实测值与预测值对比

3.2 EEMD-ARIMA模型结果与分析

由上述EEMD-ARIMA建模步骤进行模型建立。将经EEMD分解得到各分量分别进行ARIMA建模，即确定各分量满足AIC极小值准则的p、d、q值。东江流域年降水、汛期、枯水期降水数据各分量建模结果见表3。结合第2章所提到的模型评价指标，东江流域汛期、枯水期及年降水序列EEMD-ARIMA模型评价结果见表4，模型在率定期及验证期内的预测值与实测值的对比情况分别见图6、 7。

表3 东江流域季节降水各分量ARIMA建模结果

表4 EEMD-ARIMA模型预测结果评价

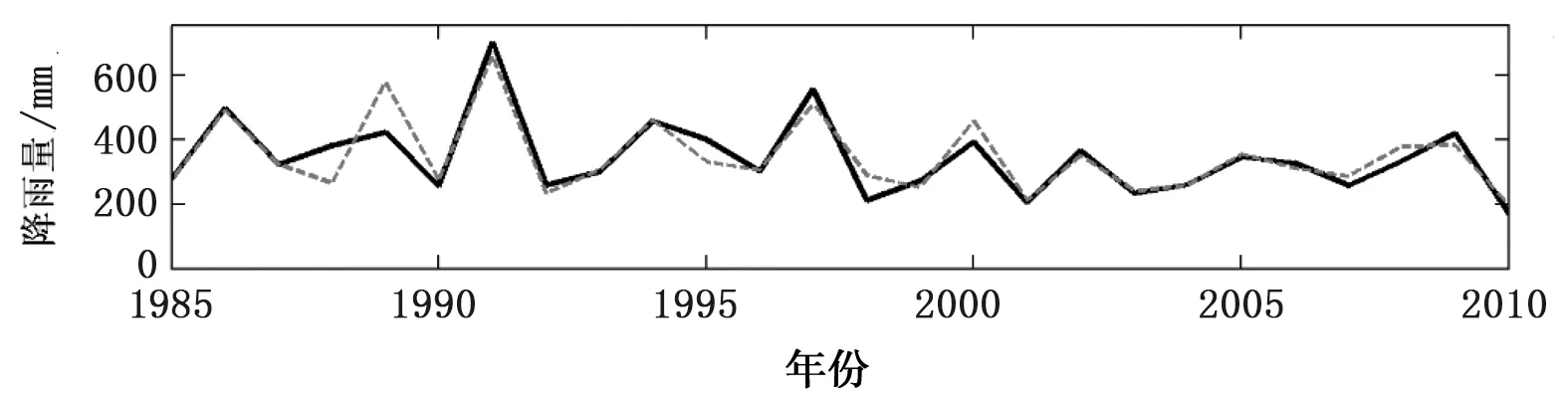
由表4、图6可知，各降水预报模型率定期内都表现出了较为理想的预测效果，表现为MAPE和NRMSE均相对较低，预测值相对于实测值的变化趋势均较为一致，且相对误差值整体较低。其中，年降水预报模型的MAPE、NRMSE分别为0.07、0.07，均为最低。而预测值与实测值相对误差在20%以内比例(0.96)和40%以内的比例(1.00)均为最高，相较于ARIMA年降水模型的MAPE(0.12)、NRMSE(0.07)、R20%(0.72)及R40%(1.00)有明显提高，表明模型具有较高的预测精度。枯水期降水预报模型的MAPE(0.09)、NRMSE(0.09)均为最大，而相对误差在20%以内比例(0.88)为最低，表明模型的预测效果相对较差，同样相对于ARIMA枯水期模型的MAPE(0.20)、NRMSE(0.62)及R20%(0.54)，其预测效果较优。另外由表可看出，枯水期的预测值与实测值的相关系数(0.91)是各模型中最高的，表明预测值的变化趋势与实测值最为接近，但在部分年的相对误差较大，导致整体的预测结果相对最差。整体而言，与单一ARIMA降水模型预测效果相比，率定期内的EEMD-ARIMA降水模型的预测精度较高。

a) 汛期降水

b) 枯水期降水

c) 年降水图6 EEMD-ARIMA模型率定期内东江流域各降水预报模型预测值与实测值对比

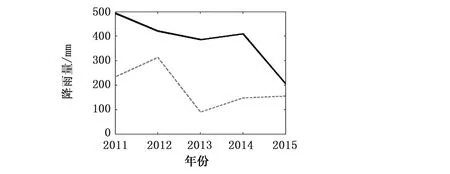
a) 汛期图7 EEMD-ARIMA模型验证期内东江流域各降水预报模型实测值与预测值对比

b) 枯水期

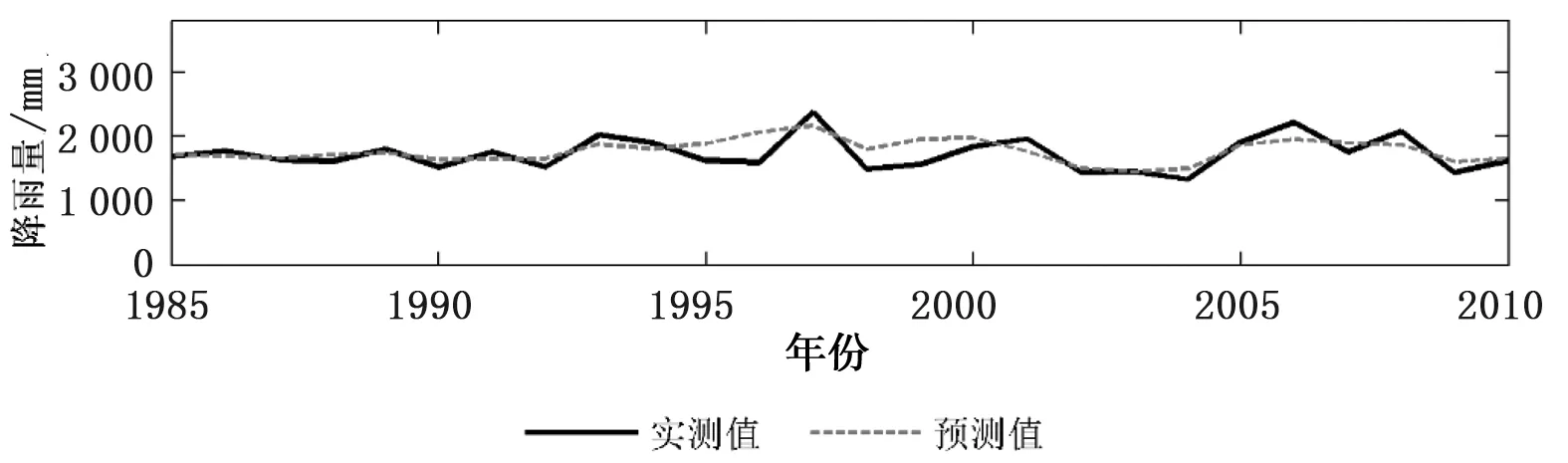
c) 年降水续图7 EEMD-ARIMA模型验证期内东江流域各降水预报模型实测值与预测值对比

由表4、图7可知，各降水预报模型验证期预测效果相比于率定期均表现出一定程度的下降趋势，但对比单一ARIMA季节降水模型，其下降程度较小。其中，年降水预报模型验证期预测效果相比于率定期下降程度较小，预测效果仍为最佳，其MAPE(0.21)和NRMSE(0.17)均为最小，预测值与实测值相对误差在20%以内比例(0.60)和40%以内的比例(0.80)均为最高，表明模型整体的预测效果较好；枯水期降水预报模型的预测效果整体而言下降趋势最为明显，其各项指标都明显低于率定期，模型预测值与实测值相对误差在20%以内比例(0.22)和40%以内的比例(0.46)均较低，表明模型的预测效果相对较差。整体而言，相对于ARIMA降水预测模型，验证期内的EEMD-ARIMA降水预测模型预测效果较优。

4 结论

本文针对现阶段东江流域长期降水预报研究不足，制约东江流域水量调度效果的问题，展开了基于EEMD的东江流域季节降水预报研究。通过对东江流域近30 a的降水时间序列分析，将东江流域降水分为汛期、枯水期和年降水3个季节进行研究，分别建立ARIMA模型及EEMD-ARIMA耦合模型，通过这2种方法对比分析以期提高东江流域季节降水预报的效果。现得到以下几点主要结论。

a) 单一的ARIMA模型对非线性东江流域降水时间序列的信息捕捉能力较差，率定期建立的ARIMA模型应用于验证期时降水预测效果较差。通过对东江流域3个季节的降水时间序列进行ARIMA模型建立，得出了一般的时间序列预测模型，整体而言，单一的ARIMA东江流域季节降水预报模型的精度相对较差。

b) 通过EEMD对原始数据的分解，能够简化模型对原始序列复杂信号的识别过程，从非平稳的原始序列中提取出准确的信息，提高了降水预报模型的精度。通过对东江流域3个季节降水时间序列先进行EEMD分解，将得到的各分量进行ARIMA模型建立，得到的EEMD-ARIMA耦合模型进行预测，相对于单一的ARIMA模型，整体而言EEMD-ARIMA模型的预测精度较高。