基于SPOT5遥感影像和DEM的河流流量估算
2019-03-28,,
,,
(1.广州市环境保护科学研究院,广东广州510620;2.黄冈中学广州学校,广东广州510800;3.水利部珠江水利委员会珠江水利综合技术中心,广东广州510611)
在有关水资源管理及洪灾管理的科学研究和业务化应用中,河流流量是一个重要变量[1]。通常情况下,它并不是直接被测量的,而是根据同步实测的水位和流速建立水位~流量关系曲线,在此基础上由观测的水位求取。该方法需要建立水文站长期进行实地观测。然而在一些经济不发达的地区只有少量的水文站,有些水文站甚至由于经费不足而关闭, Calmant 和Seyler也指出全球的水文观测网正在缩小[2]。此外,由于自然条件的限制,对某些地区河流径流长期进行实地测量较为困难,甚至无法进行实地测量[3-4]。因此,寻求一种不需要长期实地观测的估算河流流量的方法对于区域乃至全球河流径流监测具有十分重要的现实意义。
卫星遥感技术能够不接触目标而获得其信息,具有实时性、宏观性、周期性和费用低等特点。因此,利用卫星遥感技术估算河流流量并不需要长期实地观测。国内外学者先后利用不同的遥感数据进行了大尺度的水资源分析和水量估算。早期的研究根据遥感提取的河流面积与实测的流量建立面积~流量关系来估算河流流量[5]。相应地一些学者基于雷达高度计获取的河流表面高程与实测的河流流量建立经验关系估算河流流量[6-7]。此外,一些学者基于遥感获取的河宽与实测的河流流量建立经验关系估算河流流量,例如Vachtman等[8]利用遥感数据获取河流宽度,与实测流量建立宽度~流量关系进而估算河流流量。此类研究都是使用遥感手段获取的单个水文变量建立河流流量估算模型,选取不同水文变量建立的模型精度不一样。Bjerklie等人[9]指出使用水位建立的河流流量估算模型精度最好,其次是宽度,而使用流速的模型精度最差,并且指出在建立流量估算模型时使用3个水文变量会比使用1个或者2个精度更高。在此类研究中,建立流量估算模型或标定模型时需要大量的实测的河流流量数据,并且所建立的关系模型只适用于特定河段,并不具有广泛适用性。
在利用卫星遥感技术进行河流流量估算时,还有一类研究使用曼宁公式或者基于曼宁公式建立的经验公式,不需要大量实测的河流流量数据。LeFavour等[10]从Shuttle Radar Topography Mission (SRTM)数据获取比降,利用Global Rain Forest Mapping(GRFM) SAR数据获得河流宽度,用从航行图中获取的平均水深代替水力半径,在选取了一个典型的河床糙率值后,使用曼宁公式估算亚马逊河上3个断面的流量。但是使用曼宁公式估算流量时以平均水深代替水力半径往往会引入误差[11]。为了减少由此带来的误差,Jung等人[12]利用Landsat7遥感影像提取水体,得到河宽后,结合实测的河床断面获取过水断面面积和水力半径,代入曼宁公式估算河流流量,Woldemichael等人[13]也做过类似的研究。然而这些研究在估算河流流量时需要实测的河床断面,并不能应用于缺少实测河床断面的河段。此外,在这些研究中使用的遥感数据空间分辨率不高,只适用于提取宽度在数百米以上的河流,对于宽度在100 m左右的河流其提取精度较低。由于曼宁公式中糙率的确定较为复杂,于是一些研究使用基于曼宁公式建立的经验公式BJ03式估算河流流量[9,14-15],该经验公式中不包含糙率,使用起来简单方便,在难以确定糙率的河段可以使用该公式估算河流流量,然而该经验公式忽略糙率会引起一定误差。
基于以上分析可以看出目前通过卫星遥感技术估算河流流量的研究尚存在适用性不强的问题:①只适用于宽度在数百米以上的河流;②只适用于估算特定河流断面的流量。针对上述问题,本文提出了基于SPOT5遥感影像和DEM,使用曼宁公式估算流量的方法。
1 研究方法
本文选择使用曼宁公式估算河流流量。曼宁公式反映了水流与河床的部分关系以及河床内部诸多因素的相互作用,虽然它是一个经验公式,但是在水力计算中它运用广泛[16]。曼宁公式将流速表达为水面比降、水力半径和糙率的函数[17],表达如下:
V=kr2/3S1/2/n
(1)
式中V——流速,m/s;k——单位转换因子,在这里为1 m1/3s-1;r——水力半径,等于过水断面截面积除以湿周长,m;S——河段水面比降;n——曼宁粗糙系数,也叫糙率。
流量由式(2)得到:
Q=VA
(2)
式中Q——流量;A——过水断面面积。
因此,只要能够分别求出式(1)等号右边的3个未知数以及过水断面面积A,就能够估算出河流流量。
本文估算流量的具体方法如下:借助DEM数据直接获取河流上某一断面位置处的地形剖面,结合从空间分辨率为10 m的SPOT5遥感影像中得到的河流水面宽度生成过水断面,从而得到过水断面面积A和水力半径r,再根据河段上下游断面的水面高差及河段长度求取水面比降S,确定河道的糙率n后,最终代入式(1)和式(2)中求取过水断面的流量。
对比的方法为Bjerklie 等人基于曼宁公式提出了一个估算河流流量的经验公式[9],在本文中记作BJ03式。它将流量表达为河宽、平均水深以及水面比降的函数,具体表达式如下:
Q=aWbYcSd
(3)
式中Q——流量;W——河宽;Y——平均水深;S——水面比降;a、b、c、d——经验系数。
Bjerklie 等人标定的值分别为7.22、1.02、1.74、0.35[9],它们是通过1 012组河道水力要素与水量的实际测量数据得到,这些河道的水量从1~200 000 m3/s不等。BJ03式不包含糙率,使用简单方便,并且已被成功应用在不同河流流量估算中[1,14-15]。
2 研究区与数据
2.1 研究区
选定广东省东江流域为研究区域,东江是广东省重要的四大水系之一,东江干流长562 km,平均水面比降0.35‰,流域地势东北高、西南低,流域总面积35 340 km2。东江中游河段河长232 km,河道平均坡降0.31‰;下游河段河长150 km,河道平均坡降0.173‰;秋香江河长144 km,河道平均坡降1.11‰;西枝江河长176 km,河道平均坡降0.6‰[18]。东江流域水系发达,通过遥感手段估算河流流量可以作为水文站的补充。
在东江中下游河段及秋香江、西枝江上共选取7个断面进行河流流量的估算,7个断面选择在水文站不远处以便于获得实测流量进行验证。图1为研究区内选择的7个断面及水文站的空间分布。
2.2 数据
由于研究区内水面宽度从几十米到数百米不等,若使用较低空间分辨率的遥感影像,会降低提取河宽的精度。本文选择法国SPOT5卫星多光谱数据,共有4个波段,分别为绿光波段、红光波段、近红外波段、短波红外波段,其空间分辨率达到10 m(短波红外波段空间分辨率为20 m,在本文中并未用到该波段)。覆盖研究区7个河流断面需要5景SPOT5影像,影像具体的参数见表1。
采用的DEM数据是国家测绘局2002年编制的1∶50000 DEM,它是通过采集地形图上的等高线、等深线、控制点、高程点、深度点以及部分地形特征要素等,内插生成25 m×25 m的DEM数据。该DEM数据包含研究区内的水下地形。
验证使用的流量数据从广东省东江流域管理局官方网站查询得到,选择最靠近遥感影像成像时刻的流量。而对于一些断面,并没有成像时刻所对应的流量数据,只有水位数据。为了得到这些断面的验证数据,借助查询得到的其他时间的水位流量数据,拟合出该断面的水位~流量关系曲线,由最靠近成像时刻的水位求出相应的流量作为验证数据。
3 基于SPOT5影像和DEM估算断面流量
3.1 基于SPOT5遥感影像提取河流断面宽度
对SPOT5影像数据进行一系列处理,包括几何粗校正、正射校正、辐射定标、辐射校正、大气校正,并提取研究区的水域,从而提取河流断面的宽度。
在数据处理过程中,采用光照模型配准法和DEM进行配准[19],误差控制在一个像元以内。大气校正使用暗像元法,选择山体阴影区植被作为暗像元[20]。采用归一化差异水体指数NDWI(Normalized Difference Water Index)并设定一定的阈值提取水体,NDWI=(Green-NIR)/(Green+NIR)[21]。NDWI已被广泛应用在提取水体上[22],而阈值的选取对提取水体至关重要,将初步提取的结果与遥感影像叠加,通过目视判读进行微调,反复进行此步骤直到提取结果中水体边界与影像中水体边界最吻合,此时的阈值作为最优阈值。当需要从大量遥感影像中提取水体并且精度要求不是非常高时可以采用最大类间方差法(OTSU法)[23]自动确定阈值。
水体提取是河流流量遥感估算过程中最关键的步骤,若提取水体的效果不好,提取的河宽与真实河宽差别较大,则会给河流流量的估算结果带来较大误差。图2为7个断面所在区域的水体提取结果,从图中可以看出效果很好,研究区内不同宽度的河流都很清晰地被提取出来,并没有出现明显的错分和漏分。
3.2 基于DEM提取河道地形剖面
过水断面是使用曼宁公式估算河流流量的核心,为了得到过水断面,需知道河道的地形剖面。在没有实测河床断面数据的情况下,本文用ArcGIS的三维分析模块从DEM数据中获取河流断面位置处的地形剖面。图3为提取的7个断面位置处的地形剖面。从中可以看出,位于东江干流中游的枫树坝和龙川的地形剖面成V字型,而在下游的博罗的地形剖面呈U字型,与实际情况非常相符。

图3 7个断面地形剖面
3.3 计算水面比降和糙率
依据3.1和3.2的方法在研究河段的上下游分别生成2个过水断面,计算上下游断面的水面高程Hu、Hd,再量取上下游断面的距离D,由式(4)求取该河段的水面比降S。
S=(Hu-Hd)/D
(4)
在选取上下游断面的位置时,应尽量选择顺直河段,并且距离所研究的断面不宜太远,否则过长的河段中可能会有梯级大坝的存在,为水面比降的计算带来较大误差。有些研究使用河床的坡度来代替水面比降,严格意义上两者并不等同。
天然河道的糙率反映的是河床与河道壁对水流的阻碍程度,它会因河床的粗糙程度、断面形状、岸壁地质以及水流流态等的不同而不同[24]。影响糙率的因素众多,难以准确求得。在天然河道中,确定糙率最好的方法是采用该河道的实测水文资料进行推算。对于水文资料短缺或者无水文资料的河道,可以根据河道特征通过查表法比照类似河道的糙率值或者用糙率公式法计算[25]。实际计算时,可根据是否有水文资料而选择不同方法,本文使用实测水文资料分别推算7个断面所在河段的糙率。
4 结果
4.1 结果验证与分析
基于SPOT5遥感影像和DEM估算了东江流域7个断面的流量,并将各断面估算的流量与实测流量进行对比验证,具体见表2。
从表2中能够发现:估算结果中绝对误差最小的是蓝塘,为-2.71 m3/s,而绝对误差最大的断面在博罗,为-78.28 m3/s。相对误差最小的为河源,为9.02%,相对误差最大的为龙川,达到37.69%。平均相对误差在20%以内,为15.87%。整体上除了龙川断面的相对误差超过了30%,其他6个断面的相对误差皆小于20%。在这7个断面中,河宽最小达到75.51 m,2个河宽在100 m以内,3个在150 m以内。因为空间分辨率较高,所以利用SPOT5影像能够成功提取宽度在100 m左右的河流。
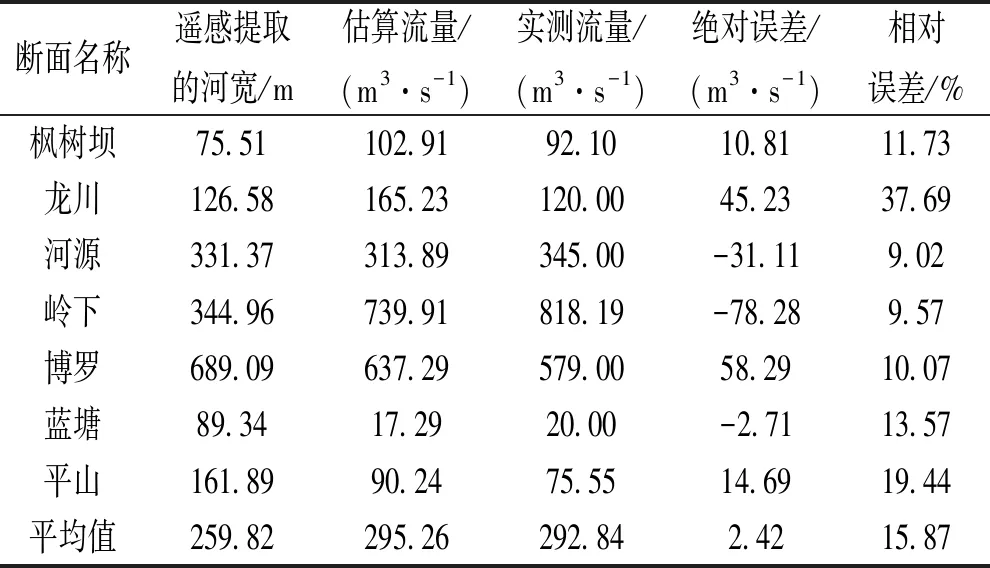
表2 估算流量和实测流量
4.2 使用曼宁公式与BJ03式估算流量结果的对比
图4为分别使用曼宁公式和BJ03式估算的流量与实测流量的对比。从图4可以看出使用BJ03式估算的流量整体上都小于使用曼宁公式估算的流量,曼宁公式估算的流量更接近于实测流量。而2种公式估算的流量均与实测流量的变化趋势一致,具有良好的相关性。
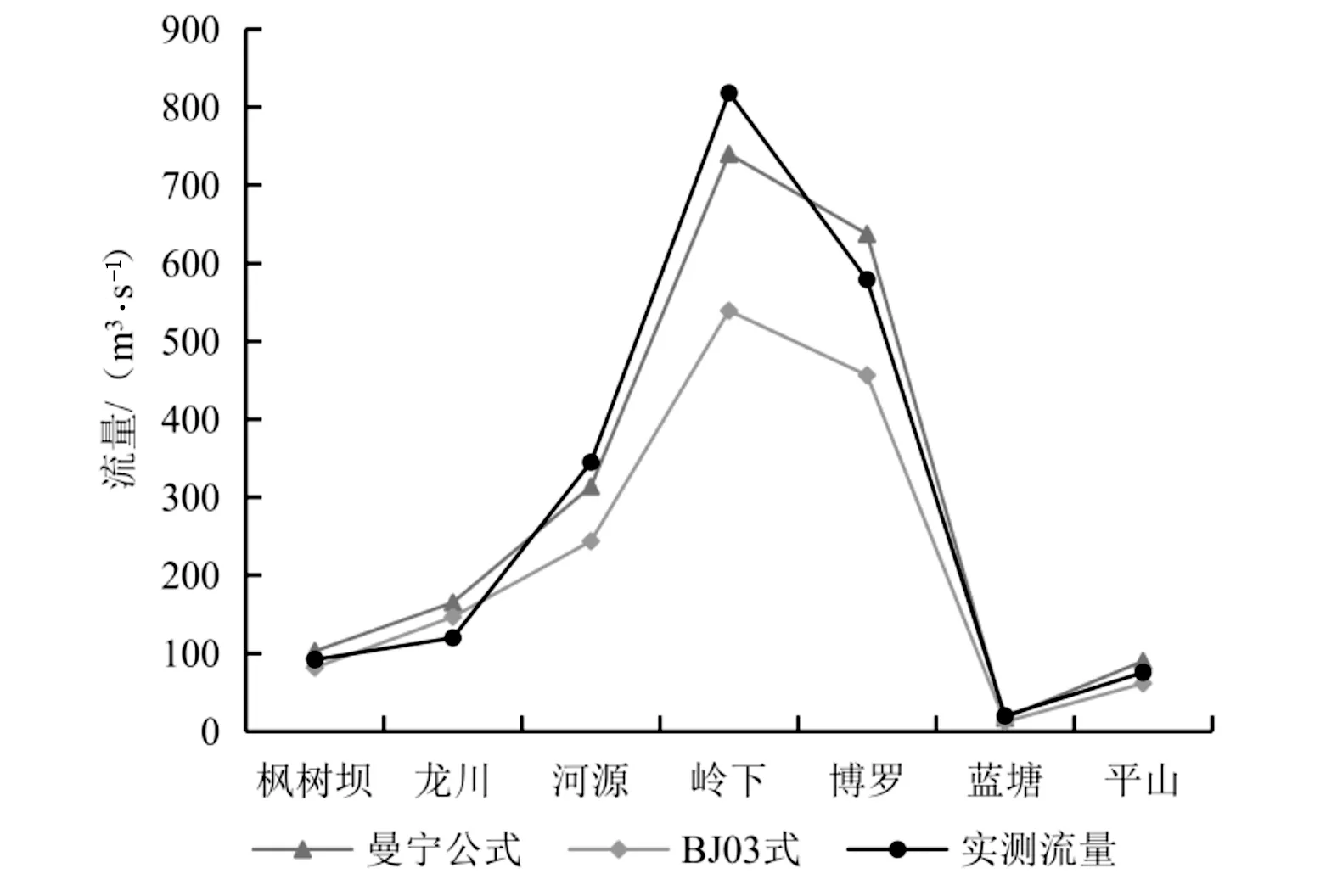
图4 2种公式估算流量与实测流量对比
表3为曼宁公式和BJ03式估算流量的误差对比。曼宁公式的绝对误差最大没有超过100 m3/s,而BJ03式估算的结果中有3个断面的绝对误差超过100 m3/s,最大达到279.06 m3/s。曼宁公式在7个断面中有4个断面的相对误差小于BJ03式,并且最大相对误差、最小相对误差以及平均相对误差都小于BJ03式。曼宁公式估算流量时有2个断面相对误差小于10%,BJ03式则没有,而相对误差小于20%的曼宁公式有6个,BJ03式只有2个。上述分析表明使用曼宁公式估算流量精度优于BJ03式。

表3 使用曼宁公式与BJ03式估算误差的对比
5 结语
本文探讨了基于SPOT5遥感影像和DEM进行河流流量估算的方法。该方法利用DEM和SPOT5遥感影像直接生成过水断面,使用曼宁公式估算流量,它不仅省时省力而且对实测水文观测数据的依赖较少,对缺乏水文资料的地区具有一定的借鉴意义。
运用该方法估算东江干流及秋香江、西枝江上7个断面的流量,平均相对误差为15.87%。分析误差产生的主要原因有:①水体边界在遥感影像上往往以混合像元的形式存在,影响提取河宽的精度;②使用的DEM数据与SPOT5影像时相不一致,在此期间人类活动可能导致河床地形发生较大变化,本研究中的龙川断面可能是此原因造成的误差偏大;③本研究使用一个固定的糙率值,实际上糙率可能随水位变化而变化,忽略这一点也会带来一定误差。
研究区内7个断面的宽度在70 ~700 m之间,最小宽度达到75.51 m,流量估算结果显示其中有6个断面的相对误差在20%以内,平均相对误差达到15.87%,而绝对误差均小于100 m3/s,说明该方法能够估算宽度在数十米以上河流的流量。若在数据精度允许的情况下,该方法借助DEM能够获取任意河流断面位置处的地形剖面,可估算任意河流断面的流量。
在龙川断面使用曼宁公式估算结果的误差较大并且大于BJ03式,其原因为:在龙川断面可能由于人类活动导致获取DEM数据时与SPOT5影像成像时河床地形发生较大变化,曼宁公式中水力半径可表达为河宽、平均水深和湿周的函数,因此曼宁公式比BJ03式多2个变量,可能使误差累积增加。尽管如此,与BJ03式对比后发现使用曼宁公式估算结果的精度整体上占优,BJ03式不考虑糙率在一定程度上增加了误差,它作为经验公式应用在其他河流的流量估算上时应重新标定系数才能取得更高的精度。
未来的工作应从混合像元分解开始,将河流边界混合像元中水域所占的丰度提取出来,以精确提取水面宽度,从而达到提高河流流量遥感估算精度的目的。此外,随着未来遥感技术的进一步发展,在多时相遥感影像支持下,基于本文方法,可得到河流的日流量和月流量等数据,而这可为实际应用提供很好的数据支撑。
