质子交换膜燃料电池不同流场接触压力有限元分析

周崇波，方 醒，阮炯明，杨庆华



质子交换膜燃料电池不同流场接触压力有限元分析

周崇波1，方 醒1，阮炯明2，杨庆华1

（1.浙江工业大学机械工程学院，浙江 杭州 310014； 2.华电电力科学研究院有限公司，浙江 杭州 310030）

质子交换膜燃料电池（PEMFC）螺栓扭矩在双极板与气体扩散层间产生接触压力，该力直接影响反应气体扩散层传质进而影响PEMFC效率。本文建立了三维有限元模型，研究不同材质和流道形式下接触压力随螺栓扭矩的变化规律。研究结果表明：石墨双极板接触压力较316L不锈钢小，分布更均匀；平行流场接触压力最大，三通道蛇形流场最小；平行流场分布均匀性最佳，新型仿生树形流场最差；平行流场螺栓扭矩在1.5~2.0 N·m间、三通道蛇形与新型仿生树形流场在2.0~2.5 N·m间存在分布均匀性极值。从优化接触压力与分布均匀性提升PEMFC性能的角度出发，应采用弹性模量小的材质以及双极板与气体扩散层直接接触面积少、流道数目多且一致化的流道形式，并使用最佳螺栓扭矩进行封装。

质子交换膜燃料电池；螺栓扭矩；流道形式；双极板材质；接触压力；有限元分析

质子交换膜燃料电池（PEMFC）不受热机卡诺循环限制，且效率高、噪声低、启动快，使得其在分布式发电、燃料电池汽车、移动式及便携式电源方面具有显著的优势，有望尽早实现商业化[1]。PEMFC装置的各部件通过螺栓连接组合在一起，在螺栓扭矩的作用下，双极板与气体扩散层之间产生接触压力，该力的作用（包括大小和分布）会引发气体扩散层孔隙率及其分布的变化，直接影响燃料和空气或氧气等反应气体向催化层的扩散，从而影响PEMFC的电化学性能。若各部件螺栓扭矩过小，引起接触压力过小，整体密封性得不到保障，而且接触不良，接触压力分布无序，造成接触电阻过大，会降低PEMFC效率；若螺栓扭矩过大，引起接触压力过大，会降低气体扩散层孔隙率，加剧接触压力分布不均匀性，增加传质阻力，甚至造成气体扩散层不可逆损坏，影响PEMFC性能[2-4]。近年来，罗鑫等研究了单边交指和单蛇形流场的电化学性能[5]；吉辰等研究了单通道流场的接触应力分布[6]；谈金祝等采用有限元模拟研究了三通道蛇形流场的接触压力分布[7-9]；李果等研究了螺栓扭矩引发的蛇形流场接触电阻变化规律[10]。

已有文献中多以蛇形流场为研究对象来分析接触压力对PEMFC性能的影响，并寻找最佳的组装螺栓扭矩。然而，不同的流场设计，包括不同的双极板材质、不同的流道形式对PEMFC组装接触压力及其分布的影响甚大[11]。为最大程度地提升PEMFC电化学性能，需要寻找更合适的材质和更合理的流道形式，以及在某种特定材质和流道形式下产生接触压力分布最均匀的螺栓扭矩。为此，本文选取2种对比材质，并设计3种不同的流道形式，即平行、三通道蛇形、新型仿生树形流道，分别建立PEMFC三维模型，研究不同流场设计（不同材质、不同流道形式）PEMFC的接触压力及其分布规律，并在此基础上，获得双极板材质、流道形式的优化原则，确定最佳螺栓扭矩区间，进而提升PEMFC的电化学性能。

1 流道形式

双极板的质量在PEMFC堆中超过60%，成本大于30%，是PEMFC的重要部件[12]。双极板流场设计包括材质、尺寸、流道等各项特征参数，并直接关系到PEMFC的性能[13]。科学有效的流场设计能使PEMFC性能提高约50%[14]。

当前研究与应用较多的流场是平行和蛇形[15]，新型流道形式包括交指形、分形、网格、仿生及其组合形式等[16-17]。Li等设计了一种提高流场均匀性的新型波浪形蛇形通道，并进行了试验研究[18]；Zeng等人采用遗传算法优化流场结构[19]；Tüber等人研究了仿生学分形流道[20]；JP.Kloess等人提出了新的仿生型分形流场，其压力损失小于蛇形与交指形流场[21]；Wang等研究了一种网状结构的仿生型流场，在提高排水性能的同时，也提升了反应流体分布均匀性[22-23]。

本文对平行、三通道蛇形、新型仿生树形3种形式流道设计进行有限元研究，图1为3种流道的形式及规格。

图1 3种流道的形式及规格

2 材质参数

目前，石墨材料因其良好的化学稳定性及高效的导电率成为当前PEMFC研究和应用最广泛的材料。金属材料如316L不锈钢，易于加工成型，而且金属的导电性能和导热性能都优于石墨。复合材料是将石墨和金属的优势结合起来，是目前双极板材质研究的重要方向[24-25]。本文PEMFC双极板材质选取了石墨和316L不锈钢，石墨及气体扩散层的材料机械性能参数见表1[8]。

表1 双极板和气体扩散层材料机械性能参数

Tab.1 Mechanical property parameters of materials for the BP and GDL

3 有限元建模

3.1 研究对象及结构模型

以接触压力分布为研究目标，研究PEMFC双极板不同流道、不同材质随组装螺栓扭矩的变化规律。

模型结构以新型仿生树形流场为例，图2为其结构。本文三维模型中，部件都采用实体单元，形变为弹性形变，根据双极板3种流场设计进行网格细化。

图2 PEMFC新型仿生树形流场结构

3.2 边界条件及载荷

PEMFC各部件、各界面均为接触组合装配，用面对面的算法定义接触关系，并采用无摩擦条件约束定义界面接触属性[8]。

本文采用标准差来分析双极板与气体扩散层接触区域的压力分布，采用接触压力平均值来表征接触压力的大小，即：

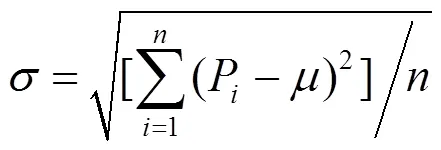
式中：为接触压力标准差；P为第节点接触压力值，MPa；为接触压力平均值，MPa；为节点数。

从式(1)、式(2)中不难发现：接触压力标准差越小，说明分布越均匀；接触压力平均值越大，表明接触压力越大。

4 模拟结果与分析

4.1 不同材质接触压力及分布

基于三通道蛇形流道，分别模拟分析石墨和316L不锈钢2种双极板在同一螺栓力矩作用下的接触压力分布。图3为模拟计算得到2.5 N·m螺栓扭矩下，316L不锈钢、石墨双极板与气体扩散层接触的压力云图。

图3 不同材质双极板接触压力云图(螺栓扭矩2.5N·m)

图4、图5分别表示2种材质在1~5 N·m螺栓扭矩下，双极板与气体扩散层接触压力的平均值与标准差。

图4 不同材料双极板接触压力平均值

由图4可见：石墨和316L不锈钢双极板接触压力变化趋势一致，其接触压力大小随着螺栓扭矩的增大而增大，这是因为螺栓扭矩越大，力的作用越大，故接触压力随着增大；石墨双极板的接触压力在同一螺栓扭矩下略小于316L不锈钢双极板接触压力，如在2.5 N·m螺栓扭矩下，石墨双极板的接触压力平均值为0.150 MPa，此时316L不锈钢双极板压力值为0.165 MPa。

图5 不同材料双极板接触压力标准差

由图5可知，标准差随着螺栓扭矩的增大，先减小，后增大。这是由于在较小的螺栓扭矩下，双极板与气体扩散层接触不良，接触压力分布趋于无序，其均匀性得不到保证，即接触压力标准差偏大，随着螺栓扭矩增大，使得接触压力均匀性不断优化，即接触压力标准差减小，但当螺栓扭矩增大到某一转折点时，接触压力增大破坏了之前建立起来的均匀性，接触压力均匀性随后变差，即接触压力标准差又不断增大。由图5还可知：在螺栓扭矩为2.0~2.5 N·m间必然存在1个极值，使得接触压力分布最均匀；石墨双极板的接触压力标准差小于316L不锈钢双极板，即接触压力分布更趋均匀。这是由于石墨材质弹性模量小，易发生弹性形变，从而使得多孔介质的气体扩散层更容易重新组织，有利于接触压力均匀分布。

4.2 不同流道形式接触压力及分布

基于平行、三通道蛇形、新型仿生树形3种流道，利用有限元方法模拟分析螺栓扭矩在1~5 N·m的接触压力分布。图6为螺栓扭矩3 N·m下3种流道形式接触压力分布。

图6 不同流道形式双极板接触压力云图(螺栓扭矩3 N·m)

图7、图8为不同流道形式下双极板接触压力平均值及标准差。

图7 不同流道形式双极板接触压力平均值

图8 不同流道形式双极板接触压力标准差

由图7可知，同一螺栓扭矩下，平行流场的接触压力平均值最大，而三通道蛇形流场的接触压力平均值最小，新型仿生树形流场接触压力平均值居中。这是因为三通道蛇形流场流程长，相应的流道数目多，双极板与气体扩散层直接接触面积最少，而多个直流道所形成的平行流场与气体扩散层直接接触面积最多。另外，由图7曲线斜率还可以看出，平行流场接触压力随螺栓扭矩的增大率大于新型仿生树形流场，而新型仿生树形流场又大于三通道蛇形流场。

由图8可知：3种流道形式的双极板接触压力标准差变化趋势相同，即先下降后上升；平行流场在螺栓扭矩1.5~2.0 N·m间存在极值，其他2种流场在2.0~2.5 N·m间存在极值；新型仿生树形流场标准差最大，平行流场标准差最小，说明新型仿生树形流场接触压力分布最不均匀，平行流场分布最均匀。这是由于平行流场的流道简洁、整齐，一致化的接触区域有利于应力均匀化，而新型仿生树形流场的流道形式在3种流道形式中最复杂，流道折角多，流程多向，不利于接触压力均匀分布。另外，从图8中经过极值点后的曲线斜率可以看出，新型仿生树形流场随着螺栓扭矩增大，其接触压力不均匀性变化率大于三通道蛇形流场，三通道蛇形流场又大于平行流场，这说明新型仿生树形流场的不均匀性增量最高，而平行流场最低，更易于接触压力均匀分布。

5 结 论

1）本文采用有限元分析方法，建立PEMFC三维模型，模拟分析了不同流场设计的接触压力大小及分布。相同螺栓扭矩下，石墨双极板的接触压力平均值与标准差较316L不锈钢双极板小，2种材质双极板在螺栓扭矩2.0~2.5 N·m间存在1个极值，可使接触压力分布最均匀。

2）相同螺栓扭矩下，平行流道形式的接触压力值最大，三通道蛇形流道形式最小；平行流道形式的接触压力值随螺栓扭矩的增加率最大，三通道蛇形流道形式最小。新型仿生树形流道形式接触压力分布的均匀性最差，平行流道形式最佳；新型仿生树形流道形式接触压力均匀性随螺栓扭矩增大的不均匀变化率最大，平行流道形式最小。

3）平行流道形式螺栓扭矩在1.5~2.0 N·m间，三通道蛇形流道形式与新型仿生树形流道形式螺栓扭矩在2.0~2.5 N·m间存在一个极值，可实现PEMFC接触压力分布均匀性最佳。

4）为优化接触压力及分布均匀性从而获得更好的PEMFC性能，应优先选用如石墨等材质弹性模量小的双极板，同时还应选取双极板与气体扩散层直接接触面积小、流道数目多且一致化的流道形式，并使用最佳的螺栓扭矩进行封装。新型复合双极板材料和新型流道形式的开发是进一步提升PEMFC性能的重要研究方向。

［1］ 王洪建, 程健, 张瑞云, 等. 质子交换膜燃料电池应用现状及分析[J]. 热力发电, 2016, 45(3): 1-7. WANG Hongjian, CHENG Jian, ZHANG Ruiyun, et al. Development and analysis of proton exchange membrane fuel cell applications[J]. Thermal Power Generation, 2016, 45(3): 1-7.

［2］ MILLER M, BAZYLAK A. A review of polymer electrolyte membrane fuel cell stack testing[J]. Journal of Power Sources, 2011, 196(2): 601-603.

［3］ SHARAF O Z, ORHAN M F. An overview of fuel cell technology: fundamentals and applications[J]. Renewable and Sustainable Energy Reviews, 2014, 32(5): 810-853.

［4］ BAZYLAK A，SINTON D，LIU Z S，et al. Effect of compression on liquid water transport and microstructure of PEMFC gas diffusion layers[J]. Journal of Power Sources, 2007, 163: 784-792.

［5］ 罗鑫, 陈士忠, 夏忠贤. 不同流场的PEMFC性能研究[J]. 电池, 2017, 47(4): 208-211. LUO Xin, CHEN Shizhong, XIA Zhongxian. PEMFC performance research of different flow field[J]. Battery Bimonthly, 2017, 47(4): 208-211.

［6］ 吉辰, 胡桂林. 装配压力对PEMFC气体扩散层影响的研究[J]. 浙江科技学院学报, 2017, 29(1): 11-16. JI Chen, HU Guilin. Study on effects of assembly pressures on the gas diffusion layer for proton exchange membrane fuel cell[J]. Journal of Zhejiang University of Science and Technology, 2017, 29(1): 11-16.

［7］ 韩雪梅, 谈金祝, 刘永昌, 等. PEM燃料电池接触压力和电化学性能的研究[J]. 太阳能学报, 2016, 37(11): 2978-2982. HAN Xuemei, TAN Jinzhu, LIU Yongchang, et al. Study on contact pressure and electrochemical performance of PEM fuel cell[J]. Acta Energiae Solaris Sinica, 2016, 37(11): 2978-2982.

［8］ 范留飞, 谈金祝, 胡学家, 等. 封装力对PEM 燃料电池气体扩散层孔隙率的影响[J]. 电源技术, 2014, 38(11): 2003-2006. FAN Liufei, TAN Jinzhu, HU Xuejia, et al. Influence of assembly force on porosity of GDL in PEM fuel cell[J]. Chinese Journal of Power Source, 2014, 38(11): 2003-2006.

［9］ 刘永昌, 胡学家, 谈金祝, 等. PEM燃料电池组装接触压力的有限元分析[J]. 电源技术, 2014, 38(10): 1818-1820.LIU Yongchang, HU Xuejia, TAN Jinzhu, et al. Finite element analysis of assembly contact pressure in PEM fuel cell[J]. Chinese Journal of Power Source, 2014, 38(10): 1818-1820.

［10］ 李果, 谈金祝, 巩建鸣. PEM 燃料电池双极板与气体扩散层界面接触电阻测量与模拟[J]. 机械工程学报, 2011, 47(8): 158-162. LI Guo, TAN Jinzhu, GONG Jianming. Measurement and simulation of contact resistance between bipolar plate and gas diffusion layer in PEM fuel cell[J]. Journal of Mechanical Engineering, 2011, 47(8): 158-162.

［11］ 肖宽, 潘牧, 詹志刚, 等. PEMFC双极板流场结构研究现状[J]. 电源技术, 2018, 42(1): 153-156. XIAO Kuan, PAN Mu, ZHAN Zhigang, et al. Research status of bipolar plate flow field structure of PEMFC[J]. Chinese Journal of Power Source, 2018, 42(1): 153-156.

［12］ LI X G, SABIR I. Review of bipolar plates in PEM fuel cells: flow-field designs[J]. International Journal of Hydrogen Energy, 2004, 30: 359-371.

［13］ 陈军, 吴懋亮, 陈峻, 等. 燃料电池双极板的3D 打印加工方法[J]. 塑料工业, 2016, 44(4): 47-50. CHEN Jun, WU Maoliang, CHEN Jun, et al. 3D printing technology for fuel cell bipolar plates[J]. China Plastics Industry, 2016, 44(4): 47-50.

［14］ WATKINS D S, DIRCKS K W, EPP D G. Fuel cell fluid flow field plate: US5108849[P]. 1992-01-01.

［15］ 陈士忠, 夏忠贤, 王艺澄, 等. 蛇形流场PEMFC性能影响因素的数值模拟[J]. 电源与技术, 2017, 41(2): 230-233. CHEN Shizhong, XIA Zhongxian, WANG Yicheng, et al. Numerical simulation of influencing factors on performance of PEMFC with serpentine flow field[J]. Chinese Journal of Power Sources, 2017, 41(2): 230-233.

［16］ ARVAY A, FRENCH J, WANG J C, et al. Nature inspired flow field designs for proton exchange membrane fuel cell[J]. International Journal of Hydrogen Energy, 2013, 38: 3717-3726.

［17］ JANG J Y, CHENG C H, LIAO W T, et al. Experimental and numerical study of proton exchange membrane fuel cell with spiral flow channels[J]. Applied Energy, 2012, 99: 67-79.

［18］ LI W, ZHANG Q, WANG C, et al. Experimental and numerical analysis of a three-dimensional flow field for PEMFCs[J]. Applied Energy, 2017, 195: 278-288.

［19］ ZENG X, GE Y, SHEN J, et al. The optimization of channels for a proton exchange membrane fuel cell applying genetic algorithm[J]. International Journal of Heat & Mass Transfer, 2017, 105: 81-89.

［20］ TÜBER K. Investigation of fractal flow-fields in portable proton exchange membrane and direct methanol fuel cells[J]. Journal of Power Sources, 2004, 131: 175-181.

［21］ KLOES S J P，WANG X，LIU J. Investigation of bio-inspired flow channel design for bipolar plates in proton exchange membrane fuel cells[J]. Journal of Power Sources, 2009, 188(1): 132-140.

［22］ WANG C T, HU Y C, ZHENG P L. Novel biometric flow slab design for improvement of PEMFC performance[J]. Applied Energy, 2010, 87(4): 1366-1375.

［23］ 苏宇静. 基于树状分形流场的质子交换膜燃料电池性能分析[D]. 杭州: 浙江工业大学, 2015: 38. SU Yujing. Performance analysis of proton exchange membrane fuel cell with fractal tree-like flow field[D]. Hangzhou: Zhejiang University of Technology, 2015: 38.

［24］ 冷巧辉, 马利, 文东辉, 等. 燃料电池双极板材料及其流场研究进展[J]. 机电工程, 2013, 30(5): 513-517. LENG Qiaohui, MA Li, WEN Donghui, et al. Research progress of bipolar plate materials and flow field for fuel cells[J]. Journal of Mechanical & Electrical Engineering, 2013, 30(5): 513-517.

［25］杨丽军, 尉海军, 朱磊, 等. 质子交换膜燃料电池双极板的研究现状及展望[J]. 金属功能材料, 2009, 16(5): 50-54. YANG Lijun, YU Haijun, ZHU Lei, et al. Present research state and prospects for bipolar plates of proton exchange membrane fuel cells[J]. Metallic Functional Materials, 2009, 16(5): 50-54.

Finite element analysis of assembly torque contact pressure for PEMFC

ZHOU Chong bo1, FANG Xing1, RUAN Jiongming2, YANG Qinghua1

(1. College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China; 2. Huadian Electric Power Research Institute Co., Ltd., Hangzhou 310030, China)

The contact pressure between bipolar plate (BP) and gas diffusion layer (GDL) directly affects the mass transfer of the gas diffusion layer, thus to affect the performance of proton exchange membrane fuel cell (PEMFC). Against this problem, a three-dimensional finite element model was built for the PEMFC, to investigate change rules of the contact pressure with assembly bolt torques under conditions with different flow fields and materials. The results show that, the graphite BP had smaller contact pressure and better uniformity than the 316L stainless steel, the parallel flow field had the largest contact pressure while the serpentine flow field had the smallest, the parallel flow field had the best uniformity while the tree bionic flow field had the worst. It is found that the contact pressure distribution for the parallel flow field had the best uniformity when the bolt torques at interzone (1.5 N·m, 2 N·m), the serpentine flow filed and the tree flow field both at interzone (2 N·m, 2.5 N·m). To improve the performance of PEMFC from view of optimizing the contact pressure and distribution uniformity, the material with small elastic modulus should be selected, the passageway with small direct contact area between the bipolar plate and the gas diffusion layer and large channel number as well as uniformity should be adopted, and the PEMFC should be packed with the most suitable bolt torque.

PEMFC, bolt torque, channel form, bipolar plate material, contact pressure, finite element analysis

TM911.4

A

10.19666/j.rlfd.201807131

周崇波, 方醒, 阮炯明, 等. 质子交换膜燃料电池不同流场接触压力有限元分析[J]. 热力发电, 2019, 48(3): 55-60. ZHOU Chongbo, FANG Xing, RUAN Jiongming, et al. Finite element analysis of assembly torque contact pressure for PEMFC[J]. Thermal Power Generation, 2019, 48(3): 55-60.

2018-7-19

周崇波(1984—)，男，博士研究生，高级工程师，主要研究方向为燃料电池、分布式能源，zhouchongbo122@126.com。

杨庆华(1964—)，男，博士，教授，博士生导师，zjutme@163.com。

（责任编辑 杨嘉蕾）