基于部队移动模式三方作战Lanchester模型研究
2019-03-28田宝国
田宝国,卢 翰,丛 凯
(海军航空大学, 山东 烟台 264001)
1914年,英国工程师F.W.Lanchester提出Lanchester方程[1],首次使用数学方法定量分析战争结果与作战双方兵力规模和火力强弱的关系。现在有许多学者针对该类方程的线性率和平方率进行研究[2-4],并针对不同情况对方程进行补充与拓展[5-11]。但是,随着武器装备和战术战法的更新,战场的环境也更加复杂,传统的Lanchester作战模型已经不适用于现代战争。于是人们在之前研究的基础上提出空间Lanchetser作战模型。考虑到在实际作战中部队在空间中的移动和部队间的相互作用,Protopoprecu等[12-13]提出空间Lanchester偏微分方程模型,同时Cosner等[14]采用具有非线性相互作用的抛物线微分方程对该模型进行理论分析。考虑到具体的空间情况,Spradlin等[15]将Lanchester方程的直接瞄准和间接瞄准进行拓展研究,并提出三维时空Lanchetser作战模型。对于三方作战的研究目前处于起步阶段[16],只是根据传统Lanchester作战模型拓展到三方作战阶段,并没有考虑到空间因素对三方作战结果的影响。同时,在当今世界出现三方作战的情况比如波斯尼亚内战、伊拉克内战和叙利亚动乱[17],基本上都是在比较复杂的山地与城市中,此时部队移动模式将对作战结果造成影响。本文对三方作战中部队移动模式进行分类分析并对其时空动力学进行研究。
1 短距移动模式
1.1 短距移动模式三方Lanchester作战模型
建立一个规模为M×N的平面二维网格,采取周期边界条件,在网格中存在A,B,C三方兵力,分别用红,黄,蓝三种颜色表示,在每一个网格中只能存在一种兵力,空格φ表示此处没有任何一方的兵力,用灰色表示。A,B,C三方和空格φ之间的关系如下所示:
(1)
(2)
其中,式(1)中μ为交战率,表示两个存在不同方兵力的网格间的发生交战并且一方占领另一方的网格的概率,体现了交战方的作战与支援能力。在实际作战中指不同部队间发现并交火的可能性。式(2)中σ为转移率,表示存在兵力的网格向空网格的转移概率,体现了交战方的个体流动性。在实际作战中指部队在区域中移动的概率。
采用蒙特卡洛随机模拟方法,具体步骤如下:
步骤1:在整个网格中随机选择一个存在兵力的网格;
步骤2:判别已经选择的网格的上下左右四个方向的网格状态;
步骤3:随机选择一个方向的网格,按照式(1)或者式(2)的反应方程进行反应;
步骤4:重复步骤1直至仿真结束。


图1 在交战率为μ时A与B的交战反应

图2 在转移率为σ时A与φ的交换反应

图3 交战反应与交换反应
1.2 交战率—转移率临界曲线
设定网格兵力的初始分布为均匀分布M=100,N=100,A,B,C三方和空格φ的比例大约为1∶1∶1∶1,交战率μ和转移率σ为可调参量,通过调整交战率μ和转移率σ,观察斑图的动态演化情况和各方的战斗、扩散情况,并记录在 15 000代时三方兵力的具体情况。
由于三方作战与传统作战有一定的不同,在作战结果方面会出现以下情况:(1)三方稳定共存,即在一定的时间内作战三方都无法被消灭。(2)两方相对稳定共存,即在一定的时间内剩余两方但两方的剩余兵力不等。(3)两方稳定共存,即在一定的时间内剩余两方且两方剩余兵力相等。(4)仅存在一方。其中两方相对稳定共存会随着仿真的继续会转化为两方共存且兵力相等情况或者仅存一方情况。
通过50次仿真模拟得到数据取均值后得出短距移动模式下交战率—转移率临界曲线为图4所示,由图可知在交战率μ≤1且转移率σ≥9时三方共存,由于此时交战率较低且转移率较高,使得部队更加趋于不同网格间的流动而不是不同兵力间的作战,故在 15 000代时三方共存。
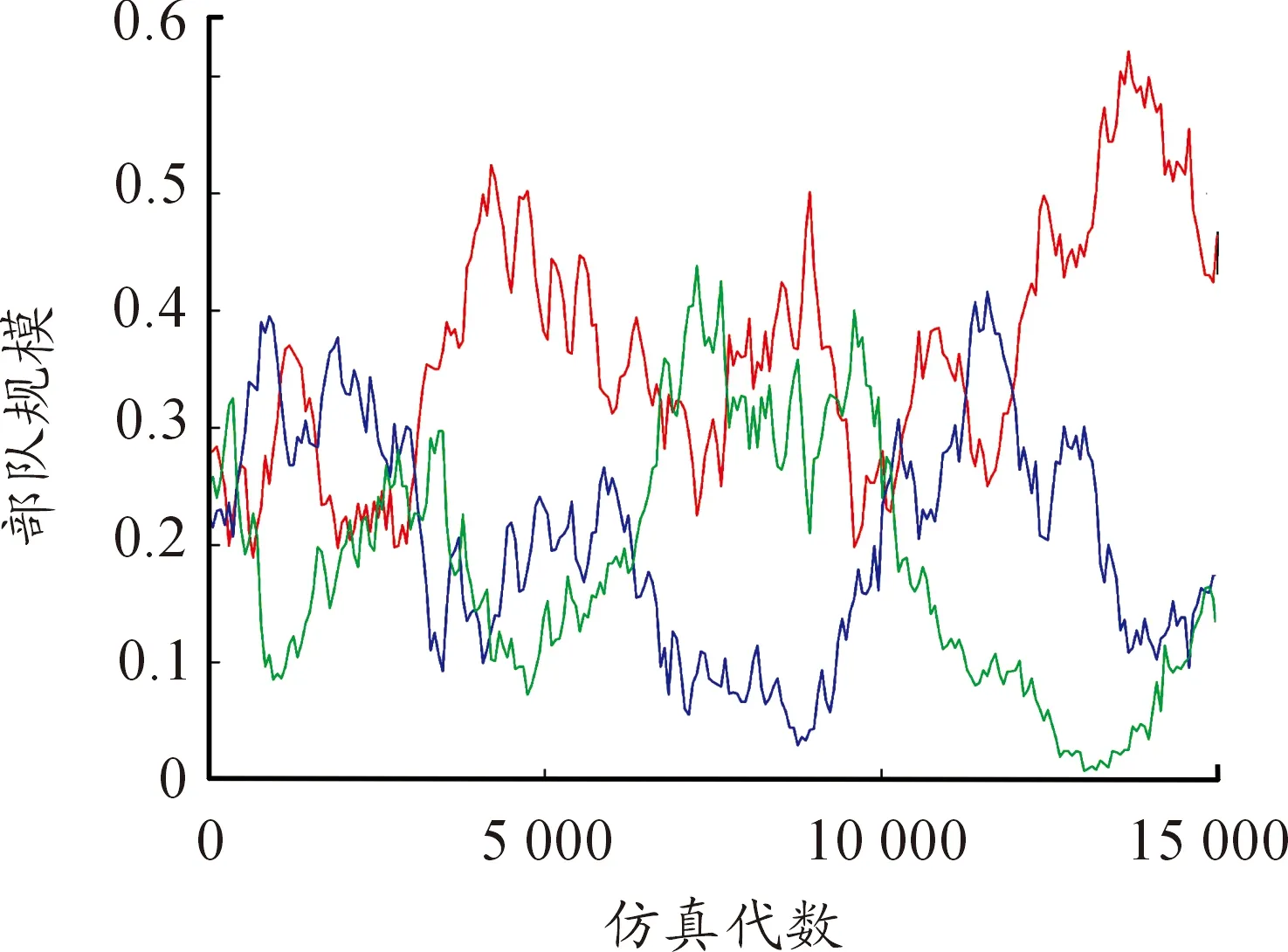
图5为当μ=0.5,σ=9.5时三方兵力的密度时间曲线。从图中可以看出,随着时间的推移,三方的兵力出现此消彼长,交替性增长和衰减的情况,彼此间相互抗衡,说明此时三方形成了稳定共存状态。
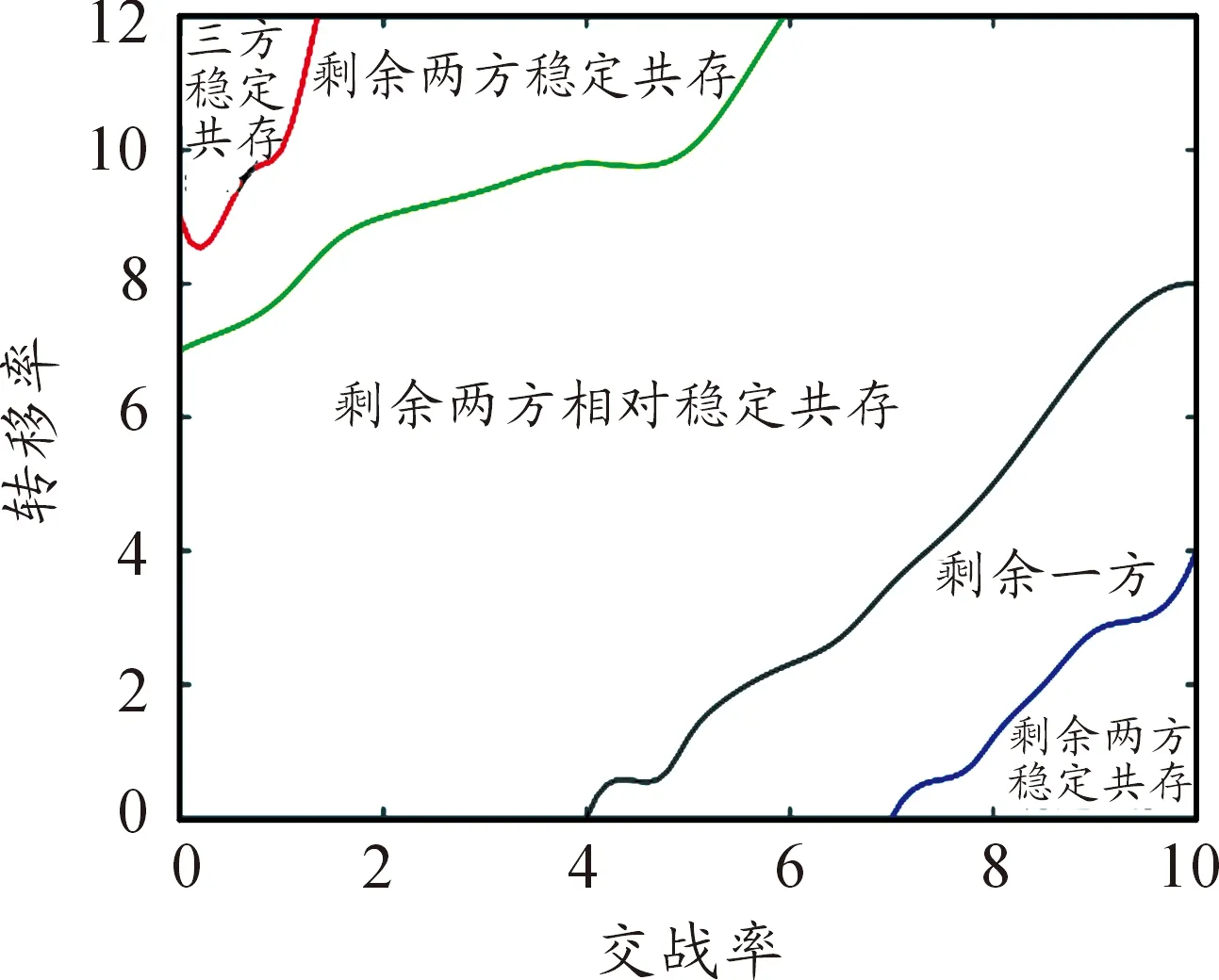
图4 短距移动模式交战率—转移率临界曲线

图5 短距移动模式μ=0.5,σ=9.5密度时间曲线
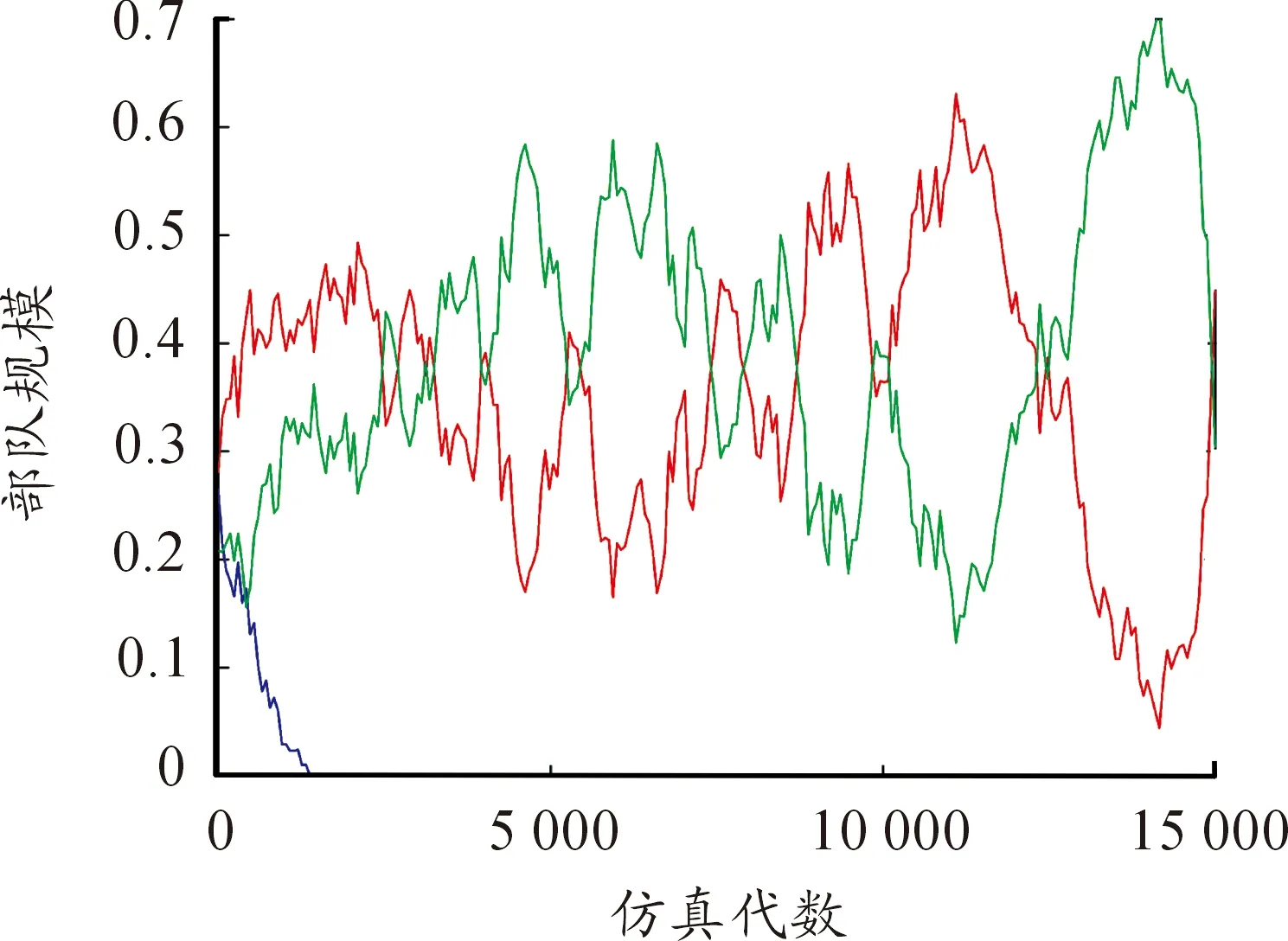
图6为当μ=3,σ=7时三方兵力的密度时间曲线。从图中可以看出,随着时间的推移,在8 000代时一方已经被完全消灭,此时只剩余两方,再经过时间的推移,剩余两方的兵力出现交替性增长和衰减情况彼此间相互抗衡,说明此时为剩余两方且稳定共存的状态。

图6 短距移动模式μ=3,σ=7密度时间曲线
图7为当μ=4,σ=4时三方兵力的密度时间曲线。从图中可以看出,随着时间的推移,在 14 000代时一方已经被完全消灭,此时只剩余两方但两方的兵力不相等,再经过时间的推移到仿真结束前,剩余两方的兵力出现交替性增长和衰减情况彼此间保持相对平衡的状态,此时为剩余两方且相对稳定的状态,对处于该状态的两方进行继续仿真得到两种状态一种问为剩余两方且稳定共存状态另一种为剩余一方状态。

图7 短距移动模式μ=4,σ=4密度时间曲线
图8为当μ=7,σ=3三方兵力的密度时间曲线。从图中可以看出,随着时间的推移,在7 500代时一方已经被完全消灭,此时只剩余两方但两方的兵力不相等,在13 500代时另一方也被完全消灭,此时只剩余一方直到仿真结束。

图8 短距移动模式μ=7,σ=3密度时间曲线
1.3 交战率μ对稳定斑图的影响
依据短距移动模式三方Lanchester作战模型,选择三方稳定共存状态研究交战率μ对稳定斑图的影响。取交战率μ=0.5转移率σ=11和交战率μ=1.5转移率σ=11两种情况的稳定斑图进行研究。根据多次实验可知,在13 000代左右斑图状态为三方稳定共存状态,13 000代和13 100代上述两种情况的斑图如图9。

图9 转移率σ=11的斑图
通过观察图9,当交战率μ=0.5时,稳定斑图中各个兵力分布较为分散,零散的斑块较多但不集中,说明此时系统的自组织性较弱,而当交战率μ=1.5时,稳定斑图中出现了多个较大的斑块,零散的斑块较少,说明此时系统的自组织性较强。再选取不同的交战率进行上述步骤观察斑图的演化结果与上述相同。故在不超出稳定状态的临界范围的情况下,交战率越大斑图的斑块越趋于集中,系统的自组织性越强。
1.4 转移率σ对稳定斑图的影响
依据短距移动模式三方Lanchester作战模型,选择三方稳定共存状态研究转移率σ对稳定斑图的影响。取交战率μ=1转移率σ=8和交战率μ=1转移率σ=11两种情况的稳定斑图进行研究。根据多次实验可知,在13000代左右斑图状态为三方稳定共存状态,故取13 000代和13 100代上述两种情况的斑图如图9、图10。

图10 交战率μ=1时的.斑图
通过观察图10,当转移率σ=8时,稳定斑图中出现了多个较大的斑块,零散的斑块较少,说明此时系统的自组织性较强。而当转移率σ=11时,稳定斑图中各个兵力分布较为分散,零散的斑块较多基本上没有形成稳定的大斑块,说明此时系统的自组织性较弱。再选取不同的交战率进行上述步骤观察斑图的演化结果与上述相同。故在不超出稳定状态的临界范围的情况下,转移率越大斑图的斑块越趋于分散,斑块间流动性越强,系统的自组织性越弱。
2 长距移动模式
2.1 Levy飞行
Levy飞行描述了由许多小步长和少量大步长组成的移动模式[19],在生物的搜索捕食行为中较为显著。已有研究发现在海洋中的一些捕食者在大范围搜捕食物过程中和野外蜜蜂回巢的过程甚至果蝇、麋鹿和信天翁等运动都存在Levy飞行方式[20,22]。Levy飞行是一种垂尾分布在大范围空间的搜索捕食中,Levy飞行是一种比布朗运动更有效的搜索策略。在作战中,使用Levy飞行策略对敌方目标进行搜索和攻击可以缩短搜索进程提高搜索效率。
Levy飞行的运动距离的概率密度为幂率分布即:
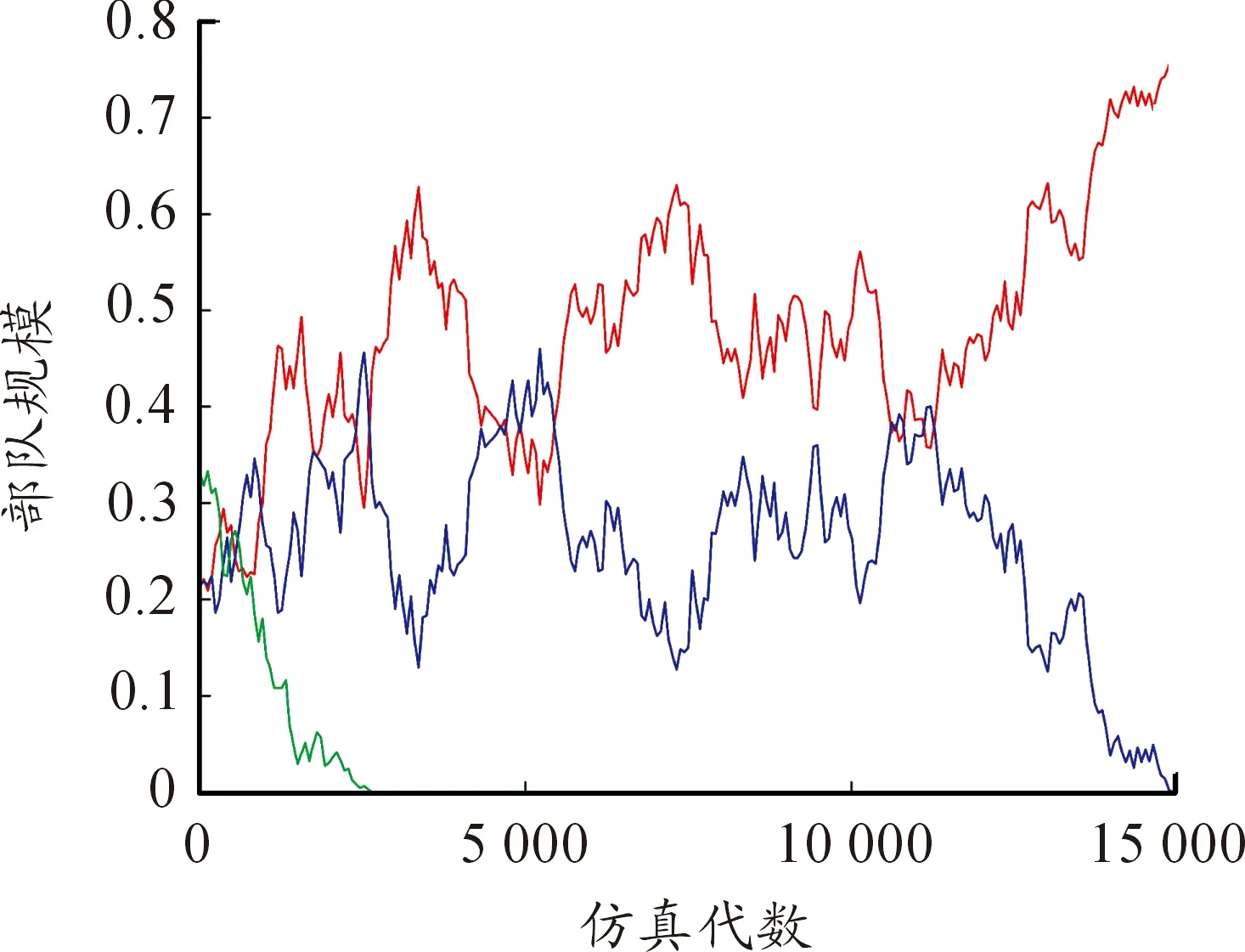
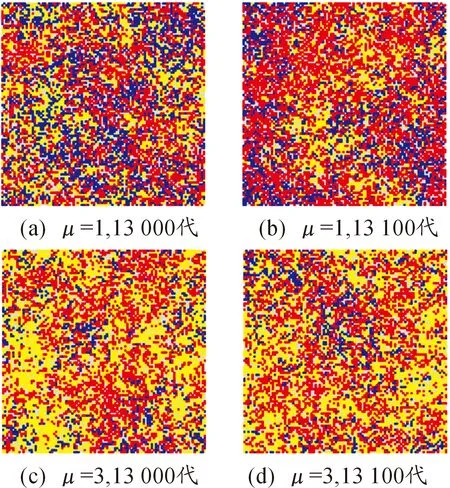
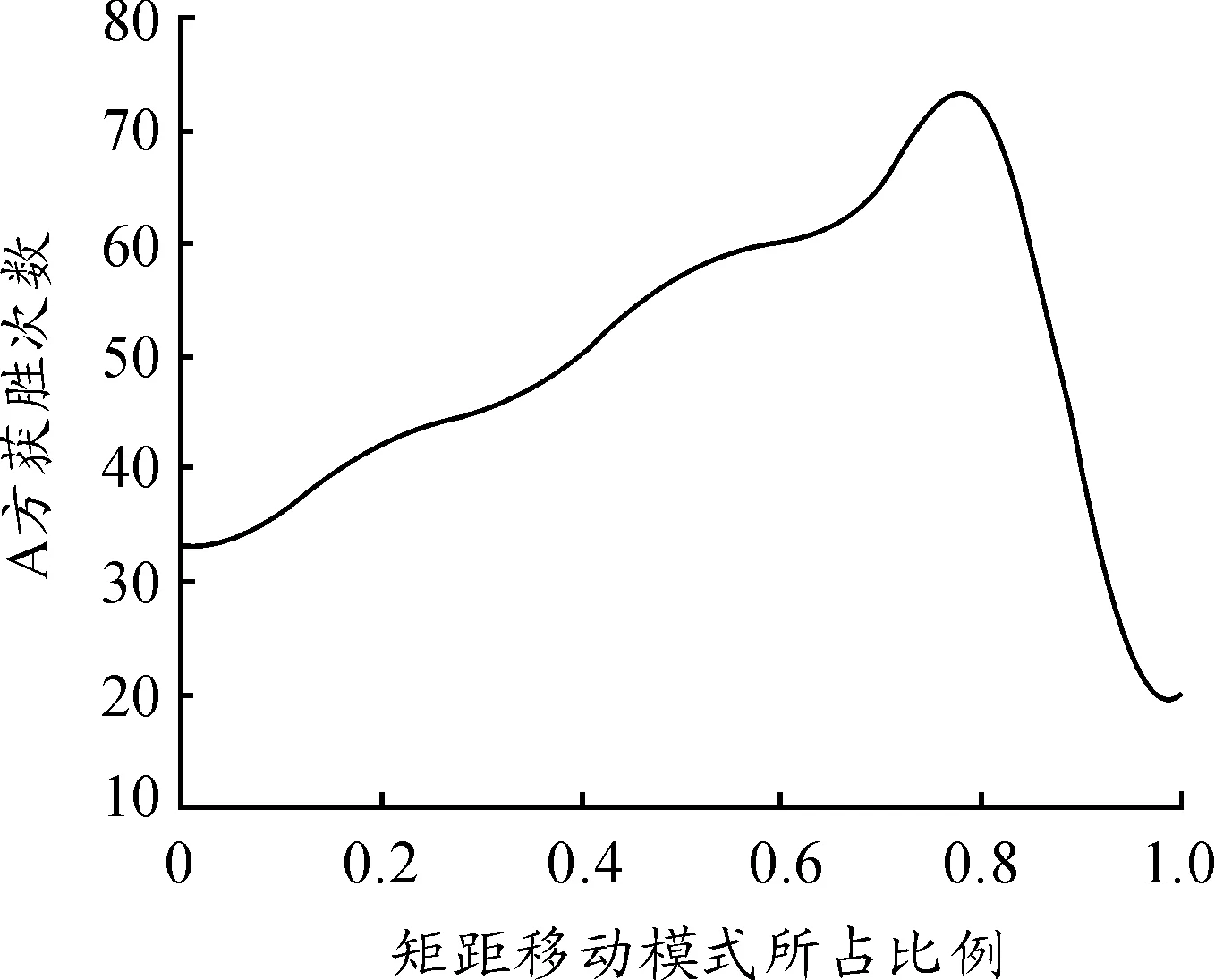
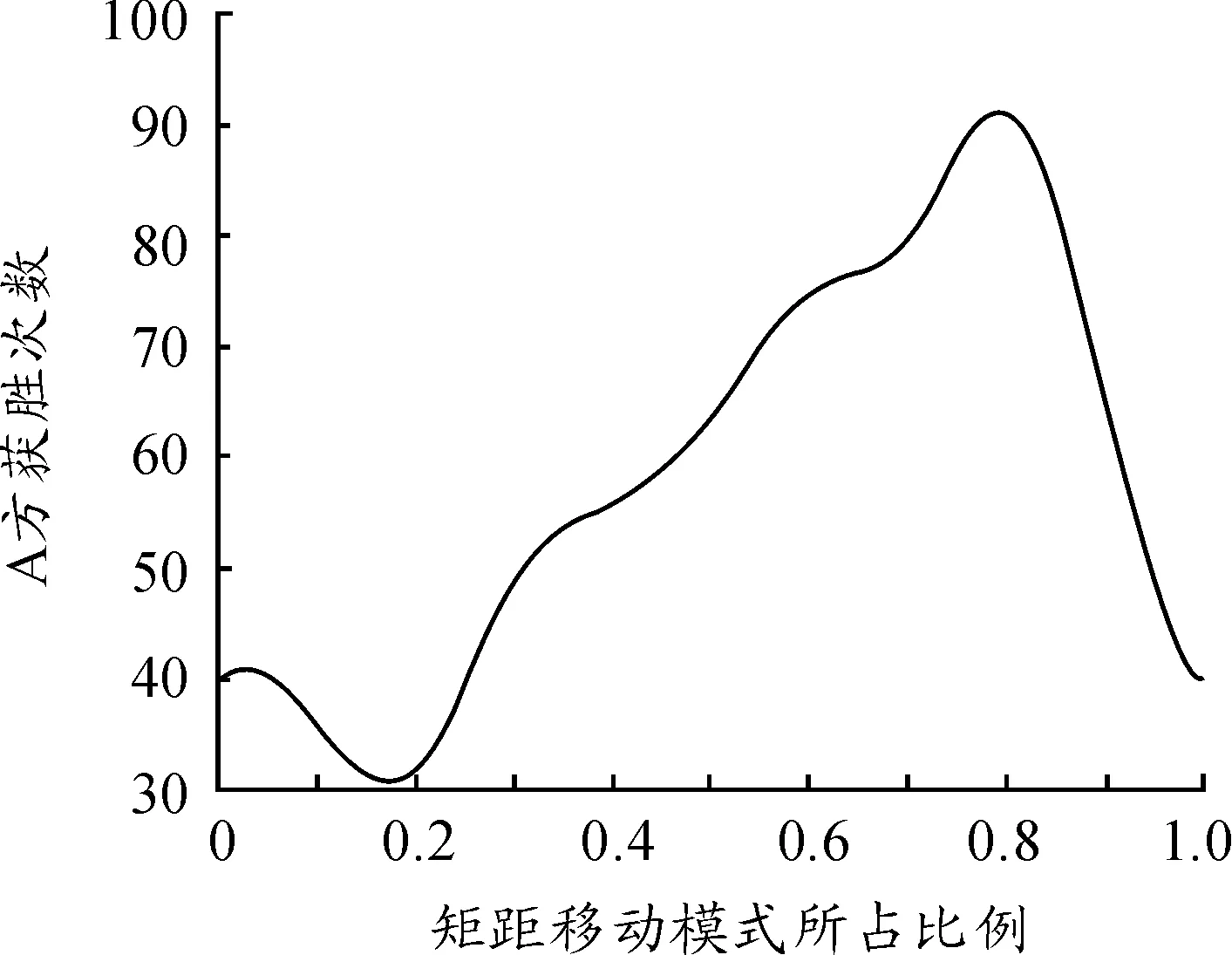
L(s)=C·s-h(1 (3) 式中,s为Levy飞行步长,s∈[s0,smax],s0为最小步长,smax为最大步长,C=(1-h)·s1-h,h为幂指数,经过研究发现,当h≈2时,为Levy飞行最优策略。 本文使用Mantegna算法[22]生成Levy飞行步长,如下所示: (4) 式中U、V满足正态分布: (5) 标准差σU、σV满足下式: (6) 式中,Γ(z)为gamma函数。 图11为Levy飞行的飞行轨迹。 图11 Levy飞行轨迹 采用与第一章相同的M×N平面网格,A,B,C三方和空格φ之间的相互作用与式(1)式(2)相同,采用蒙特卡洛随机模拟方法,具体步骤如下: 步骤1:在整个网格中随机选择一个存在兵力的网格; 步骤2:使用蒙特卡洛方法确定下一个网格处于现在网格的方向;按照式(4)计算Levy飞行步长; 步骤3:根据计算的方向和步长确定网格与步骤1确定的网格,按照式(1)或者式(2)的反应方程进行反应; 步骤4:重复步骤1直至仿真结束。 取网格兵力的初始分布为均匀分布M=100,N=100,A,B,C三方和空格φ的比例大约为1∶1∶1∶1,Levy飞行参数β=2,s0=2,smax=20。交战率μ和转移率σ为可调参量,通过调整交战率μ和转移率σ,观察斑图的动态演化情况和各方的战斗、扩散情况,并记录在15 000代时三方兵力的具体情况。 通过50次仿真模拟得到数据取均值后得出短距移动模式下交战率—转移率临界曲线为图12所示,通过观察并与图4作对比发现,长距移动模式下各个状态的临界曲线与短距模式下有较大不同,在相同交战率情况下长距移动模式三方稳定共存的情况相对于短距移动模式转移率较低,同时长距移动模式下出现两方相对稳定共存的情况的在图中所占面积与短距相比较小。与短距移动模式相比,在长距移动模式下,两方稳定共存状态的所占面积较大。由于Levy飞行使得系统中斑块间的流动性增大,故相对减少了系统的自组织性,为了保持和原系统相似的状态,需在同等条件下增大交战率或者减少转移率以增大系统的自组织性或减少斑块间的流动性。 图12 长距移动模式交战率—转移率临界曲线 图13为当μ=0.5,σ=8时三方兵力的密度时间曲线,随着时间的推移,三方的兵力出现此消彼长情况,彼此间相互抗衡,说明此时三方形成了稳定共存状态。图14为当μ=3,σ=6时三方兵力的密度时间曲线。从图中可以看出,随着时间的推移,在1 000代时一方已经被完全消灭,此时只剩余两方,之后剩余两方的兵力彼此间相互抗衡,说明此时为剩余两方且稳定共存的状态。 图13 长距移动模式μ=0.5,σ=8密度时间曲线 图15为当μ=5,σ=5时三方兵力的密度时间曲线,随着时间的推移,在2 000代时一方已经被完全消灭,此时只剩余两方但两方的兵力不相等,再经过时间的推移到仿真结束前,剩余两方的兵力出现交替性增长和衰减情况彼此间保持相对平衡的状态,此时为剩余两方且相对稳定的状态,对处于该状态的两方进行继续仿真得到两种状态一种为剩余两方且稳定共存状态另一种为剩余一方状态。 图14 长距移动模式μ=3,σ=6密度时间曲线 图16为当μ=6,σ=3三方兵力的密度时间曲线,随着时间的推移,在2 000代时一方已经被完全消灭,此时只剩余两方但两方的兵力不相等,在15 000代时另一方也被完全消灭,此时只剩余一方直到仿真结束。 图15 长距移动模式μ=5,σ=5密度时间曲线 图16 长距移动模式μ=6,σ=3密度时间曲线 依据长距移动模式三方Lanchester作战模型,选择三方稳定共存状态研究交战率μ对稳定斑图的影响。取交战率μ=1转移率σ=10和交战率μ=3转移率σ=10两种情况的稳定斑图进行研究。根据多次实验可知,在10 000代左右斑图状态为三方稳定共存状态,故取10 000代和10 100代上述两种情况的斑图如图17。 图17 转移率σ=10的斑图 通过观察图17,在第10 000代时斑图中有一些较大的斑块中存在一些较小的斑块,而在10 100代时这些小的斑块将大斑块侵蚀消灭,这是由于Levy飞行增加了不同网格间兵力的流动,使得在短距状态下无法发生的交战在长距状态下便可以发生,故大斑块会被小斑块消灭。当交战率μ=1时,稳定斑图中各个兵力分布较为分散,零散的斑块较多且不集中,说明此时系统的自组织性较弱,而当交战率μ=3时,稳定斑图中出现了多个较大的斑块,零散的斑块较少,说明此时系统的自组织性较强。再选取不同的交战率进行上述步骤观察斑图的演化结果与上述相同。故在不超出稳定状态的临界范围的情况下,交战率越大斑图的斑块越趋于集中,系统的自组织性越强。 据短距移动模式三方Lanchester作战模型,选择三方稳定共存状态研究转移率σ对稳定斑图的影响。取交战率μ=0.5转移率σ=7和交战率μ=0.5转移率σ=10两种情况的稳定斑图进行研究。根据多次实验可知,在10 000代左右斑图状态为三方稳定共存状态,故取10 000代和10 100代上述两种情况的斑图如图18。 图18 交战率μ=0.5时的斑图 通过观察图18,当转移率σ=10时,稳定斑图中各个兵力分布较为分散,零散的斑块较多基本上没有形成稳定的大斑块,说明此时系统的自组织性较弱。而当转移率σ=7时,稳定斑图中出现了多个较大的斑块,说明此时网格间部队流动减少系统的自组织性较强。再选取不同的交战率进行上述步骤观察斑图的演化结果与上述相同。故在不超出稳定状态的临界范围的情况下,转移率越大斑图的斑块越趋于分散,网格间部队流动性越强,系统的自组织性越弱。 采用与第一章相同的平面网格,三方和空格之间的相互作用与式(1)式(2)相同,部队的移动模式不仅仅为短距或者Levy飞行,先采用蒙特卡洛随机模拟方法确定网格的具体移动模式,在进行斑块间的反应,具体步骤如下: 步骤1:在整个网格中随机选择一个存在兵力的网格; 步骤2:采用蒙特卡洛随机模拟方法确定网格的具体的移动模式; 步骤3:若移动模式为Levy飞行模式,使用蒙特卡洛方法确定下一个网格处于现在网格的方向;按照式(4)计算Levy飞行步长;若移动模式为短距移动模式则判别已经选择的网格的上下左右四个方向的网格状态; 步骤4:若移动模式Levy飞行模式为根据计算的方向和步长确定网格与步骤1确定的网格按照式(1)或者式(2)的反应方程进行反应;若移动模式为短距移动模式则随机选择一个方向的网格按照式(1)或者式(2)的反应方程进行反应; 步骤5:重复步骤1直至仿真结束。 取网格兵力的初始分布为均匀分布,三方和空格的比例大约为,Levy飞行参数。短距移动模式选择概率为交战率和转移率为可调参量,通过调整交战率和转移率,观察斑图的动态演化情况和各方的战斗、扩散情况,并记录在15 000代时三方兵力的具体情况。 通过50次仿真模拟得到数据取均值后得出短距移动模式下交战率—转移率临界曲线为图19所示,通过观察并与图4、图12作对比发现,在混合移动移动模式下各个状态的临界曲线与短距和长距模式下有较大不同,在相同交战率情况下混合移动模式三方稳定共存的情况相对于短距移动模式转移率较低而基本上与长距移动模式相同,混合移动模式下出现两方相对稳定共存的情况的在图中所占面积与其他两种移动模式相比较小,而两方稳定共存状态的所占面积较大。由于Levy飞行使得系统中斑块间的流动性增大,故相对减少了系统的自组织性,但由于混合移动模式下网格间的移动为Levy飞行模式和短距模式共同作用,使得系统的自组织性减少的同时,通过这种混合移动模式使得系统的稳定性得到增加,故稳定共存的面积得到了增加。 图19 混合移动模式交战率—转移率临界曲线 依据混合移动模式三方Lanchester作战模型,选择三方稳定共存状态研究交战率μ对稳定斑图的影响。取交战率μ=0.5转移率σ=9和交战率μ=1.5转移率σ=9两种情况的稳定斑图进行研究。根据多次实验可知,在12 000代左右斑图状态为三方稳定共存状态,故取12 000代和12 100代上述两种情况的斑图如图20。 图20 转移率σ=9时的斑图 通过观察图20,当交战率μ=0.5时,斑图中各个兵力较为分散,但也有少量的同种兵力聚集的斑块,并且12 000代和12 100代的斑图差别较大,说明此时系统的自组织性较差不同网格间兵力的流动性较强。当交战率μ=1.5时,在 12 000代时斑图中出现了较大的同种兵力聚集的斑块,在这些斑块附近也分散着一些零散的斑块,在12 100代时斑图中一些斑块被消灭分散但也出现了一些新的同种兵力聚集的较大斑块,说明此时系统有一定的自组织性并且不同网格间兵力的流动性也较强。再选取不同的交战率进行上述步骤观察斑图的演化结果与上述相同。故在不超出稳定状态的临界范围的情况下,交战率越大斑图的斑块越趋于集中,系统的自组织性越强。 据混合移动模式三方Lanchester作战模型,选择三方稳定共存状态研究转移率μ对稳定斑图的影响。取交战率μ=1转移率σ=8和交战率μ=1转移率σ=11两种情况的稳定斑图进行研究。根据多次实验可知,在12 000代左右斑图状态为三方稳定共存状态,故取12 000代和12 100代上述两种情况的斑图如图21。 图21 交战率μ=1时的斑图 通过观察图21,当转移率σ=11时,斑图中各个兵力较为分散并且12 000代和12 100代的斑图差别较大,说明此时系统的自组织性较差不同网格间兵力的流动性较强。当转移率σ=8时,在12 000代时斑图中出现了较大的同种兵力聚集的斑块,在这些斑块附近也分散着一些零散的斑块,在12 100代时斑图中一些斑块被消灭分散但也出现了一些新的同种兵力聚集的较大斑块,说明此时系统有一定的自组织性并且不同网格间兵力的流动性也较强。再选取不同的交战率进行上述步骤观察斑图的演化结果与上述相同。故在不超出稳定状态的临界范围的情况下,转移越大斑图的斑块越趋于分散,网格间不同兵力的流动性越强。 由3.2节可知,Ps为在实际仿真中选择短距移动模式的概率,即移动模式为短距移动模式部队在整个部队中所占比值。部队参加作战最终的目的应为消灭敌人,保存自己,所以应选择三方作战最终只剩一方的情况进行分析。在三方兵力中选择A方使用混合移动模式其兵力用红色表示,其余两方兵力用黄色和蓝色表示,空格φ用灰色表示三方的兵力比为A,B,C三方和空格φ的比例大约为1∶1∶1∶1,Levy飞行参数β=2,s0=2,smax=20,μ=5,σ=1,ps为可调变量。分三种情况,其余两方皆为短距移动模式,其余两方皆为长距移动模式和一方为短距移动模式一方为长距移动模式。调节ps,并在每一个值进行100次仿真A方获胜次数绘制曲线图如图22~图24所示。 图22 其余方为短距移动模式A方获胜次数曲线 图23 其余方为长距移动模式A方获胜次数曲线 图24 其余方一方为长距移动模式一方为短距移动模式A方获胜次数曲线 通过图22~图24可知当ps=0.8时即短距移动模式和长距移动模式部队的比值为4∶1时,红方获胜次数最多,同时可知,当A方仅有短距移动模式时,部队的获胜次数最少,而增加了长距移动模式的兵力后获胜次数增加,当短距移动模式和长距移动模式部队的比值小于1∶1时,部队的获胜次数开始下降。由于Levy飞行增加了部队的自由度和攻击半径,使得其在对抗中可以攻击到短距移动模式下无法攻击的部队,同时当长距移动模式比值过大时由于增加了部队的自由度使得部队不易聚集在一起反而会使得部队容易被攻击故在不断增加长程移动模式兵力后会使得部队的获胜次数下降。 1) 本文提出了交战率μ和转移率σ为影响作战过程的变量,通过仿真得到在不同模型下的交战率—转移率临界曲线,确定了不同稳定状态下交战率和转移率的取值范围。 2) 交战率的增大会增强系统的同种兵力间聚合能力,使斑块增大,增强系统的自组织性。转移率的增加会加速不同网格间兵力的移动,加速系统的流动性。 3) 加入Levy飞行移动模式后,系统的流动性得到加强,同一种状态的临界曲线上的交战率取值增大,转移率取值减少。 4) 混合移动模式下短距移动模式部队和长距移动模式部队的最佳比值为4∶1。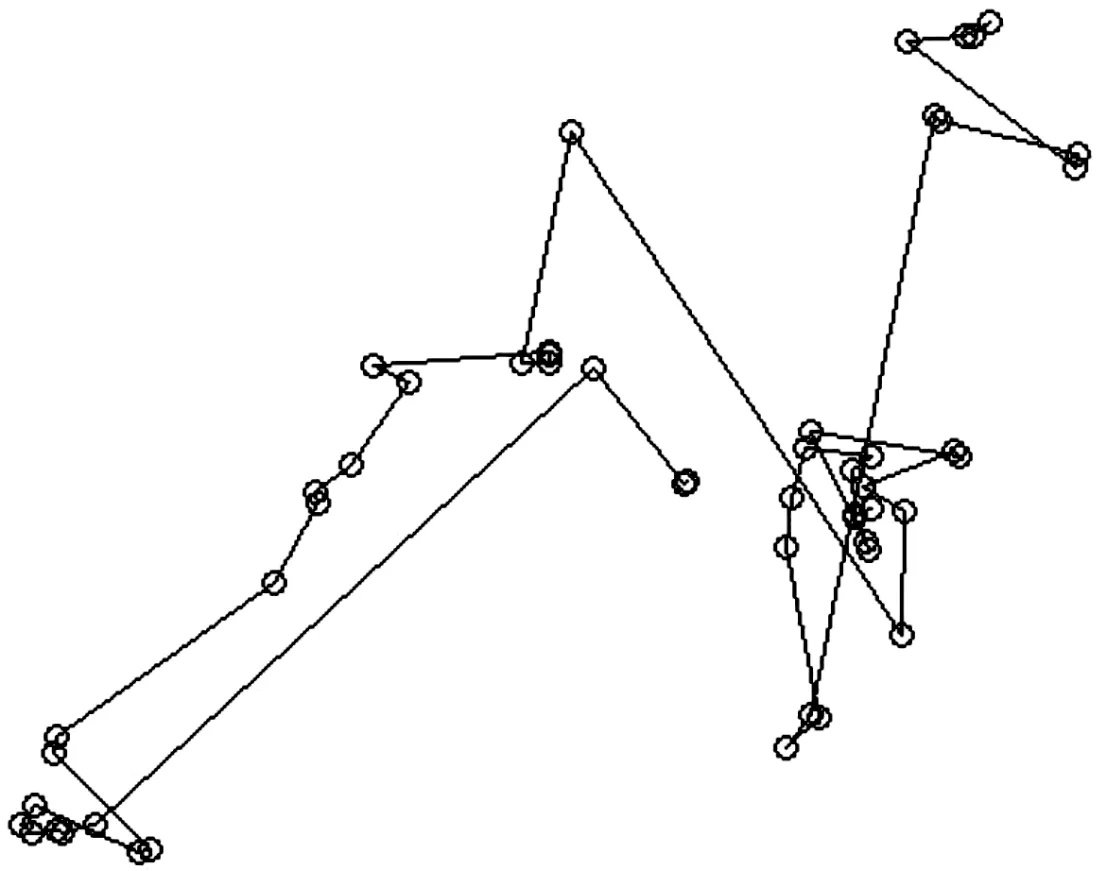
2.2 长距移动模式三方Lanchester作战模型


2.3 交战率μ对稳定斑图的影响
2.4 转移率σ对稳定斑图的影响

3 混合移动模式
3.1 混合移动模式三方Lanchester作战模型
3.2 交战率—转移率临界曲线

3.3 交战率μ对稳定斑图的影响

3.4 转移率σ对稳定斑图的影响

3.5 短距移动模式与长距移动模式最佳部队比值

4 结论
