基于跑车试验的连续梁桥承载能力快速评定方法研究

李伟钊

(广西交投科技有限公司 南宁市 530001)

桥梁作为交通运输的重要枢纽，及时掌握其结构工作性能，保障运营安全是人们广泛关注的课题。对既有桥梁结构，若能快速、准确地评定其工作状态和安全性能，就可以为桥梁管理部门提供科学的决策信息，使得桥梁养护、加固措施和投资方案合理有效。目前桥梁评定方法中应用最广泛且相对可信的为荷载试验评定法，荷载试验评定法中又分为静载试验评定法和动载试验评定法。在桥梁结构试验中，主要借助于静载试验来评定结构的承载能力，动载响应测试分析处于辅助地位，用于结构状态的定性分析。静载试验法具有测试技术简单、成熟，测试数据精度高等优点，但其测试过程复杂、测试时间长、需要完全封闭桥梁交通、不经济等缺点使得其应用受到显著限制。在应用动力试验进行桥梁评定方面，国内外学者进行了相应研究，周敉、贺拴海[1]，胡刚、王丰[2]基于简支梁频率与刚度的内在关系来对单梁承载力进行评定；施洲[3]系统研究了基于动力测试的桥梁结构损伤识别及性能评定理论与应用； Lu ZR、Law SS[4]，徐伟华、吕中荣[5]，王树栋、卜建清[6]，单德山、李乔[7]等学者研究了基于移动荷载响应的桥梁结构损伤识别及评估理论。桥梁动力特性受桥梁质量、刚度、环境以及边界条件变异的影响，车辆作用下的动力响应还受汽车特性、车速以及桥梁不平整等因素影响；若直接用其来评定结构的刚度，难度较大，难以应用到工程实际。车辆作用下的动力响应中包含着静力响应，若能从中分离出静力响应，则可套用静力荷载试验的方法来进行桥梁评定。

1 简支梁振动位移理论分析

由动力学理论可知[8]，在匀速移动常量力F作用下等截面简支梁的动力响应y(x，t)可表示为：

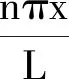
(1)

在匀速移动简谐力F1cospt作用下等截面简支梁的动力响应y1(x，t)可表示为：

(2)

注意到：

(3)

因此，移动常量力F作用下在x处产生的静挠度yst可用相应的级数近似表示为：

(4)

令α=ϖ1/ω，则y0d(x，t)可写为：

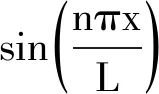
=yst(x，t)+ysd(x，t)

(5)

在公路桥梁上，汽车受到路面不平整度的激励后，以车辆的固有频率发生振动而通过桥梁时，车辆簧上质量的惯性力就是一种移动的简谐力。因此，行驶汽车对桥的作用可以看作是移动常量力(汽车的自重)和简谐力的叠加。

在移动汽车荷载作用下，简支梁的竖向位移可综合式(1)、式(2)、式(5)得到：

y(x，t)=yst(x，t)+ysd(x，t)-y0f(x，t)+y1(x，t)

(6)

若考虑简支梁的粘性阻尼，竖向位移的表达式跟不考虑阻尼时相似，同样为振动频率为n、n、p+n、p-n的4类振动的组合，不再赘述。对于多个移动荷载，可通过叠加原理运用上述结论；对于连续梁桥，利用结构力学方法可以去除多余约束，简化为简支梁，上述结论同样适用。

2 仿真分析

某3×40m的连续梁桥，截面面积A=1.4m2，惯矩为0.676m4，弹性模量E=3.5104MPa，密度=2600kg/m3；泊松比=0.2，车辆采用单自由度模型，质量为25000kg，悬挂刚度k=3000kN/m，悬挂阻尼30kN/s，如图1；假定结构的阻尼比为0.05；则桥梁的一阶频率为2.503Hz，车辆自振频率为1.744Hz。桥面不平整度参照文献[9]计算，等级取“好”。参照文献[10]的方法，基于newmark积分，采用分离迭代法计算车辆过桥时桥梁的振动响应。

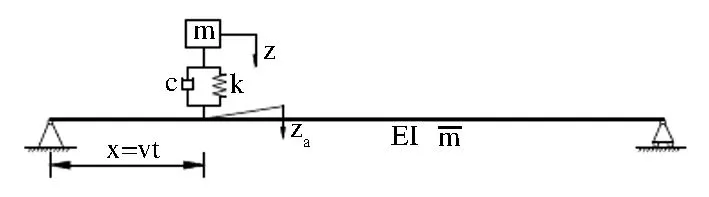
图1 单自由度车辆模型

车辆以v=10m/s通过本桥时中跨跨中处位移及加速度时程曲线自功率谱幅频曲线如图2所示；由加速度自功率谱幅频曲线可以看出，振动部分的优势频率为1.855Hz、2.087Hz，由位移自功率谱幅频曲线可以看出，静力位移部分能量集中在0.4028Hz以下频段。综合两幅频曲线，可以取低通滤波截止频率为0.403Hz，图3为中跨跨中的挠度时程曲线，可以看出，滤波后的挠度曲线跟实际静挠度曲线吻合较好，方法可以准确地从动挠度时程曲线中分离出静力位移。

3 实桥应用

某桥为变截面预应力混凝土连续梁桥，混凝土等级为C50，汽车荷载设计等级为公路-I级，跨径组合为45+50+77+77+50+45=344m。单向四车道，横向布置为：2.0m人行道+0.5m防撞栏+0.5m路缘带+(3.75+3.53=14.25m)机动车道+0.5m防撞栏+0.5m中央间隔=18.5m。梁高2.3～4.6m，梁底曲线为二次抛物线，桥梁纵断面图(半桥)见图4。

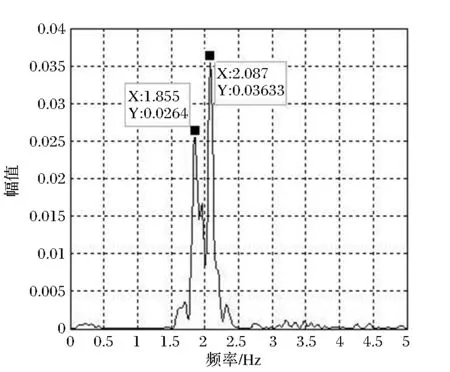
(a)加速度

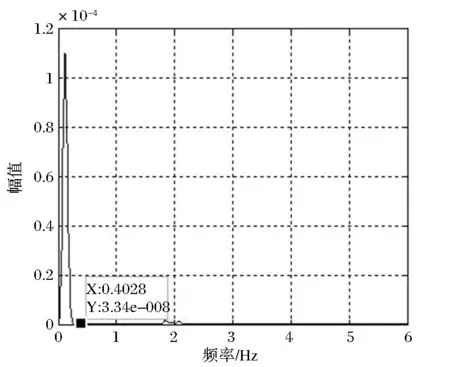
(b)位移图2 中跨跨中处加速度及位移时程曲线自功率谱幅频曲线

图3 3×40m连续梁在v=10m/s中跨跨中挠度时程曲线

本桥静载试验共分3个工况，分别测试截面A、B、C的挠度；加载车辆采用总重30t的中国一汽解放翻斗车，车辆参数见表1。跑车试验用两台试验车对称于桥梁中轴线分别以不同速度并排匀速通过桥梁，同时测定截面A、B、C的挠度曲线以及加速度曲线。

按照仿真分析的方法对实测动挠度曲线进行低通滤波，可得到该动挠度响应中的静挠度和动态成分，限于篇幅，图5、图6、图7给出各测试截面在v=40km/h的挠度时程曲线。将滤波静挠度曲线的时间轴改为距离轴后即得到该截面在跑车车辆作用下的广义影响线，按静载试验工况在滤波广义影响线上布置车辆，可计算得到对应的静载试验挠度估算值。

表1 加载车辆参数

图4 桥梁纵断面图(cm)

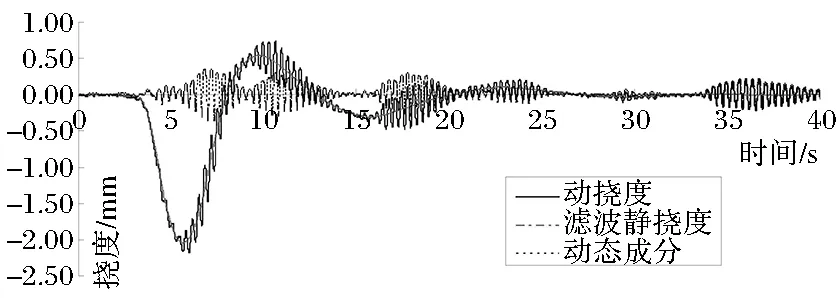
图5 v=40km/h时截面A实测挠度时程曲线

图6 v=40km/h时截面B实测挠度时程曲线

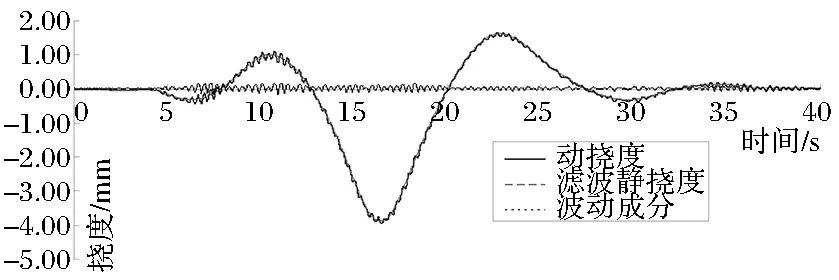
图7 v=40km/h时截面C实测挠度时程曲线

数据处理时把试验用的三轴车辆换算为单轴车辆，车辆在桥上行驶距离为桥长与车辆前后轮距之和。对于本桥，汽车在第1跨行驶距离为45+3.23=48.23m；在第6跨行驶距离为45+1.27=46.27m；在其他跨上行驶距离等于该跨跨径。汽车在桥上不能保证完全匀速行驶，在数据处理时认为汽车在各跨内速度是相等的。静载试验各加载工况挠度实测值与基于跑车试验广义影响线得到对应静挠度估算值见表2。

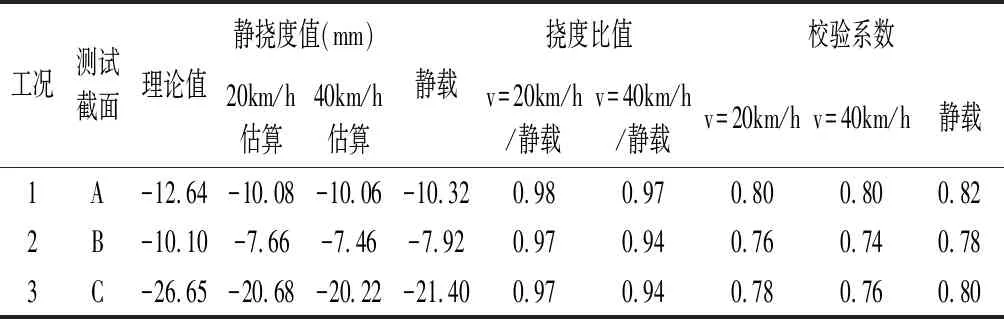
表2 连续梁桥各测试截面挠度结果汇总

从表2可以看出在通过低通滤波处理得到的跑车车辆广义影响线上布置车辆所得到的挠度估算值与实际静载试验所得到的数据基本一致，但比静载试验所测挠度值小，比值均大于0.94；速度越低时所得到的挠度估算值与静载试验值越接近。

挠度估算值与静载试验实测值差异主要原因分析如下：

(1)混凝土为非线性材料，在荷载作用下桥梁响应存在滞后性，在车辆低速行驶时桥梁变形较为充分，变形值较大。静载试验实测值是在加载变形稳定后测量，其理应比估算值大。

(2)实际静载试验加载车以及跑车试验车辆的车重与计算采用的300kN存在一定偏差；静载试验时车辆位置跟加载方案位置略有差异；跑车过程中车辆不能始终保持并排、匀速、对称。

利用挠度估算值除以相应的理论计算值得到挠度校验系数后，可按照规范相关方法对本桥进行承载力评定。本桥基于跑车试验广义影响线估算挠度得到的各截面最大挠度校验系数见表2，可以看出方法结果与静载试验结果基本一致，可代替静载试验进行桥梁承载能力快速评定。

4 结论

(2)荷载作用下桥梁响应存在滞后性，在通过低通滤波处理得到的跑车车辆广义影响线上布置车辆所得到的挠度估算值比静载试验所测挠度值小，速度越低时挠度估算值与静载试验值越接近。可考虑对不同速度下挠度估算值乘以修正系数来得到静载试验下的实测挠度，修正系数有待进一步研究。

(3)基于跑车试验得到的挠度校验系数与静载试验基本相当，可在不中断或者少中断交通的情况下代替静载试验，对梁式桥进行承载力快速评定。