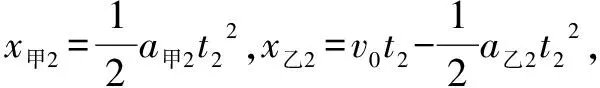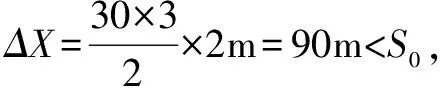谈“追及相遇问题”的解题技巧

潘科选

(山西省芮城县第一职业学校 044600)

追及相遇问题是高中物理运动学部分的一类重要题型，解决此类问题，需要根据运动学公式寻找物体的空间位置关系.

一、题型分析

①若前面物体速度比后面物体快，则它们将逐渐远离；

②若后面物体速度比前面物体快，则它们将逐渐靠近.

题型1：①→②：速度相等时有最远距离；

题型2：②→①：A.没追上的情况下，速度相等时有最近距离，不能相遇；B.速度相等时恰好追上的情况下只能相遇一次；C.速度相等前已经追上的情况下会相遇两次.

二、解题方法概述

1.物理分析法

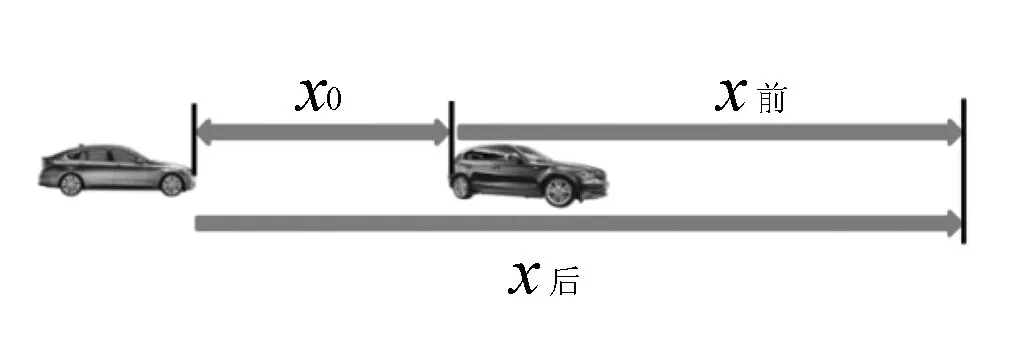
图1

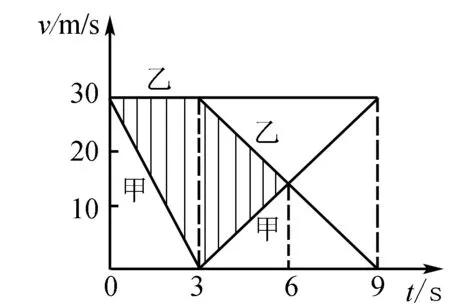
若前面物体速度比后面物体快，则它们将逐渐远离；若后面物体速度比前面物体快时，如图1所示，恰好不相撞的临界条件是：速度相同时恰好相遇(空间同一位置)，在此之后V后

2.数学分析法

设经历时间t相遇，根据空间位置关系，得出关于t的一元二次方程(至少有一个物体做变速运动)，对判别式分析讨论，若Δ=0，则相遇或刚好追上；若Δ>0，有两个解，则物体相遇两次；若Δ<0，则追不上或不能相碰.

3.图象法

在同一坐标系中画出两物体的v-t图象，然后利用图象求解.

4.相对运动法

巧妙地选取参照系，然后找两物体的相对运动关系.

例题高速公路上甲乙两车在同一车道上同向行驶，甲车在前，乙车在后，速度均为v0=30m/s，距离s0=100m，t=0时刻甲车遇紧急情况后，甲乙两车的加速度随时间变化如图2所示，取运动方向为正方向．通过计算说明两车在0～9s内会不会相撞？

图2

分析开始时两车相距100m，甲车在前，乙车在后，初速度均为30m/s；0-3s内甲车做匀减速直线运动，乙车做匀速直线运动，这段时间内乙车的速度大于甲车的速度，甲、乙两车相互靠近；3s末甲车速度减为零，乙车速度仍为30m/s；3-9s内甲车做匀加速直线运动，乙车做匀减速直线运动，6s末两车速度相等；3-6s内乙车的速度大于甲车的速度，甲、乙两车继续相互靠近；若6s末乙车仍未追上甲车，以后乙车的速度小于甲车的速度，两车不会再相撞.

解法一物理分析法

3s末，v甲=v0-a甲1t1=0，v乙=v0=30m/s；

3-9s内，设经过t2时间甲乙速度相同，则a甲2t2=v0-a乙2t2，得t2=3s；

故0-6s内，x甲=x甲1+x甲2=67.5m，x乙=x乙1+x乙2=157.5m，因x乙

解法二：数学分析法

代入数据化简得：t22-6t2+11=0，因Δ<0，该方程无解，故0-9s内两车不会碰撞.

解法三：图象法

如图3所示,作出9s内甲、乙两车的v-t图象；

图3

阴影面积表示甲、乙两车的位移之差，用ΔX表示，如果ΔX≤S0，则两车不会相撞；

解法四：相对运动法

以甲车为参考系，则0时刻乙车相对于甲车的速度为v相对1=v0-v0=0，乙车相对于甲车的加速度为a相对1=0-a甲1=10m/s2；

3s末，乙车相对于甲车的速度为v相对2=a相对1t1=30m/s；

0-6s内，乙车相对甲车的位移x相对=x相对1+x相对2=90m