轨道客车多维速度检测信息的数据融合技术
2019-03-27赵海波
朱 彦 赵海波
(中车长春轨道客车股份有限公司总体研发部, 130062, 长春//第一作者, 教授级高级工程师)
随着科技的发展和乘客对轨道客车要求的提高,“安全、可靠、绿色、智能、高颜值”已经成为轨道客车的新发展方向。轨道客车的速度信息是重要的检测数据,直接关系到列车控制系统和信号系统等多个控制系统的控制过程。如何获得真实和可靠的速度信息是提升轨道客车安全性的重要保障。本文旨在研究充分应用各种传感器的特点,将不同检测机理的速度信息进行数据融合,以期获取真实可靠的轨道客车速度信息。
1 速度信息获取方式
目前,轨道客车一般通过安装在列车上的速度传感器或其他速度监测装置来获得各自独立的速度信息。速度传感器及速度监测装置主要包括:基于霍尔或光电效应的轴端速度传感器;基于多普勒效应的多普勒雷达;基于北斗卫星的北斗导航系统;基于惯性器件的惯性导航系统。
1.1 轴端速度传感器
轴端速度传感器安装于车辆轴端(见图1)。在车辆运行时,传感器检测车轴的转速并输出脉冲信号,信号接收器计算脉冲信号数量,并结合车辆轮径等参数计算出车辆的运行速度[1]。
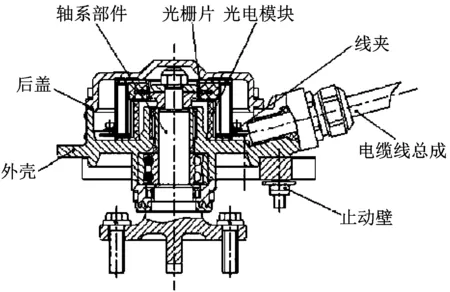
图1 轴端速度传感器结构示意图
车辆的速度计算如下:
v=3.6 πdf/n
(1)
式中:
v——轨道客车运行速度;
d——轨道客车轮径;
f——速度传感器输出信号频率;
n——车轮每转脉冲次数。
1.2 多普勒雷达
多普勒雷达通常安装于轨道客车车下(见图2)[2]。在轨道客车运行时,多普勒雷达向地面发送电磁波并利用反射波与发射波的频率差,依据多普勒频移公式计算列车速度。

图2 多普勒雷达结构示意图
车辆的速度计算如下:
v=fd/m
(2)
式中:
fd——雷达输出频率;
m——车辆运行每米脉冲次数。
1.3 北斗导航系统
北斗导航系统是我国自行研发的卫星导航系统,其基本原理与GPS(全球定位系统)类似,为被动式导航。北斗导航系统通过接收北斗卫星信号进行载体的定位和测速(需要接收至少4颗北斗卫星的信号,见图3)。目前,北斗导航系统的载波相位测试精度已经达到了GPS的水平[3]。

图3 北斗导航系统列车测速示意图
1.4 惯性导航系统
惯性导航系统(见图4)为主动式导航系统,其基本原理是利用惯性原理和加速度计实现对载体的速度、姿态及位置等状态的测试,且测试信号不受外界条件的干扰。
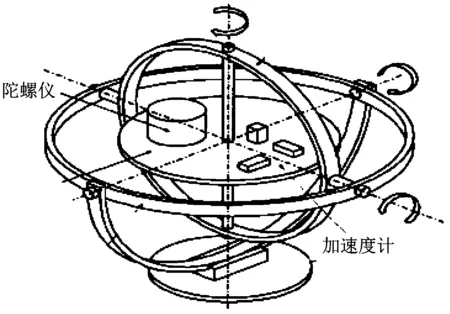
图4 惯性导航系统结构示意图
1.5 各测速装置的测试精度分析
通过对轴端速度传感器、多普勒雷达、北斗导航系统及惯性导航系统的原理分析,以及他们在轨道客车上的实际运用情况分析,得出的轨道客车测速装置性能比较结果如表1所示。
通过表1可知,无论单独使用哪种测速装置,都无法完全满足轨道客车对速度测试的要求。因此,有必要利用数据融合技术,将多种测速装置的测试数据进行融合处理,通过最优状态估计等方法,获得正确与可靠的速度信息,从而提升轨道客车的运行安全性。
2 多维数据融合
多维数据融合是指采用不同的测速装置对轨道客车进行速度测试,然后利用数据配准、关联及融合等技术,计算获取轨道客车速度的最优估计信息的数据处理技术。
2.1 卡尔曼滤波
卡尔曼滤波是一种数据处理方法。凡是需要从被噪声污染的信号中确定信号波形或状态的,都可采用卡尔曼滤波。卡尔曼滤波的主要特点是引入了现代控制理论中的状态空间概念,即将所要估计的信号作为状态,用状态方程来描述系统,因而能够解决多维非平稳随机过程的估计问题。卡尔曼滤波算法采用递推计算方法,不需要了解过去时刻的测量值,只需根据当前时刻的测量值和前一时刻的估计值,即可递推计算出所需信号当前时刻的估计值,因此在数据融合领域有着广泛应用。
卡尔曼滤波的计算流程如图5所示。卡尔曼滤波的基本公式表示如下:
状态方程
Xk=Φk,k-1Xk-1+Wk-1
(1)
量测方程
Zk=HkXk+Vk
(2)
状态预测方程
(3)
协方差预测方程
(4)
滤波增益方程
(5)
滤波估计方程
(6)
滤波协方差更新方程
Pk=(I-KkHk)Pk,k-1
(7)
滤波器初始状态条件
(8)
式中:
k——时刻;
Xk——系统状态向量;
Φk——状态转移矩阵;
Wk——系统噪声矩阵;
Zk——状态量测矩阵;
Hk——量测转移矩阵;
Vk——量测噪声矩阵;

Pk——状态估计误差的协方差矩阵;
Kk——卡尔曼滤波增益;
Qk——系统噪声的协方差矩阵;
Rk——量测噪声的协方差矩阵;
E——期望均值。
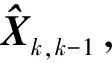
2.2 数据融合
选用模糊式卡尔曼滤波算法,对多维传感器数据进行数据融合,实现对轨道客车速度的最优估计(见图6)。
在一个采样周期t内,可将车辆的加速过程看成匀加速过程,所建立的状态方程如下:
(9)
式中:
ak、vk、sk——分别为车辆的加速度、速度和位移的状态值;
vax、vdo、vbd、vin——分别为轴端速度传感器、多普勒雷达、北斗导航系统及惯性导航系统的速度输出值;
ain——惯性导航系统的加速度输出值。
利用式(1)~(9),可以求解出卡尔曼滤波状态估计值,实现对车辆速度信息的融合。
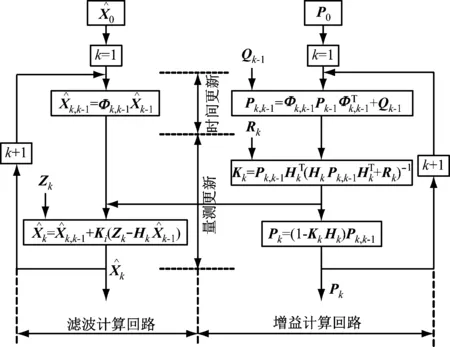
图5 卡尔曼滤波计算流程
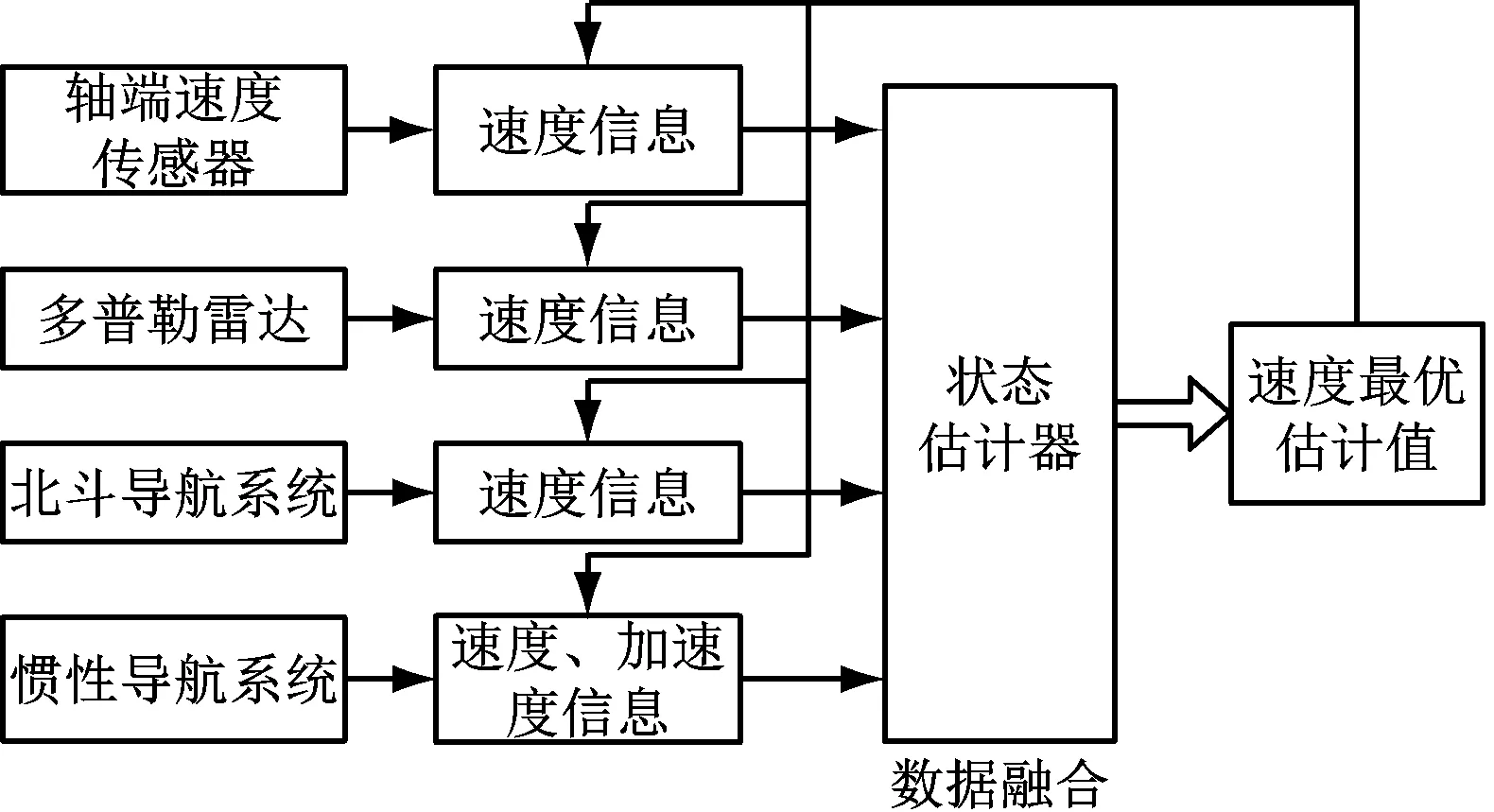
图6 多维传感器数据融合结构
2.3 速度估计过程分析
轨道客车在正常行驶时,固定参数的卡尔曼滤波器能够将4种传感器检测到的速度信息进行数据融合,完成对量测噪声的过滤,并对速度信息进行估计,输出可靠的速度估计值。
但是,当一种或者多种速度测量值发生波动或者突变时,固定参数的卡尔曼滤波器会发生滤波发散,速度估计值会与真实速度存在较大差异,无法满足轨道客车运行的要求。同时,根据大量的实际运行经验,轨道客车在空转/滑行往往和雨雪等恶劣天气同时发生,因此需要采用扩展式滤波算法,在算法中根据工况的不同改变测量噪声的值,调整速度信息和加速度信息在量测更新过程中的占比,提高对速度数据的估计精度[4-5]。速度测量值出现波动的工况与信号如表2所示。

表2 传感器数据波动工况
考虑到速度测量值出现波动的原因是运行工况变化引起的,并不是车辆真实速度发生了突变,因此,车辆的加速度测量信息可以认为是准确的,可以通过加速度信息对速度信息进行估计和过滤,调整量测值在滤波过程中的权重(见图7)。

图7 调整量测噪声结构图
惯性导航系统输出的加速度信息是由加速度计测试的,而加速度计的测量误差是由于车辆运行过程中的振动等原因引起的(方向与列车运行方向垂直)。本文给出的加速度信息主要是在列车速度突变工况下(车轮空转和打滑、部分速度信号丢失等)对速度进行修正,所以仅需加速度信息中与列车运行方向同向或反向的信息,故加速度的测量误差可以不计,即可以将加速度测量值近似等同于估计值和真实值[6]。
3 仿真分析
通过计算机仿真软件对滤波算法进行验证。仿真分析条件设定如下:
(1) 列车运行速度:从0启动后加速到350 km/h(误差控制:小于±2 km/h),保持恒速运行10 min,然后实施最大的常用制动,直至列车停止。
(2) 工况:在列车恒速运行时,分别模拟列车打滑、进入隧道、遇雨或遇雪工况,每种工况持续时间为60 s;
仿真结果如图8~11所示。通过图中数据对比可以看出,扩展式卡尔曼滤波算法能够有效地利用加速度数据,在线调整量测噪声的权重,充分发挥卡尔曼滤波算法的递推式最优估计的优越性,达到消除噪声干扰的目的,由此提高轨道客车测速系统的可靠性和稳定性。

图8 固定滤波与扩展滤波算法的速度估计值
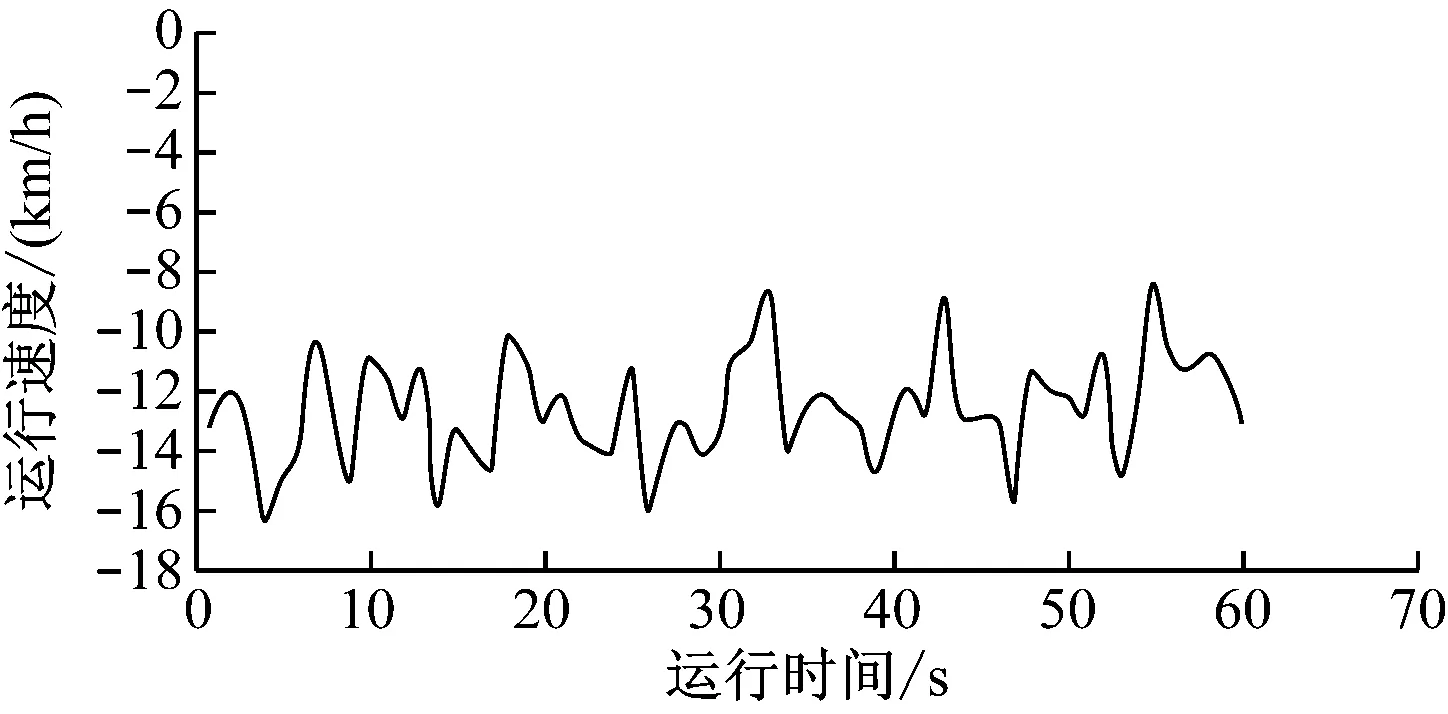
图9 车辆打滑时两种算法速度差
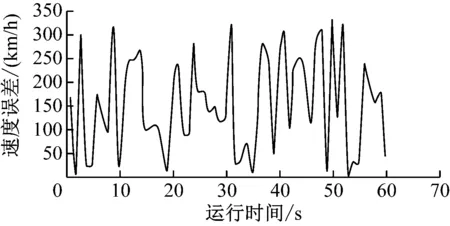
图10 车辆进入隧道时两种算法速度差
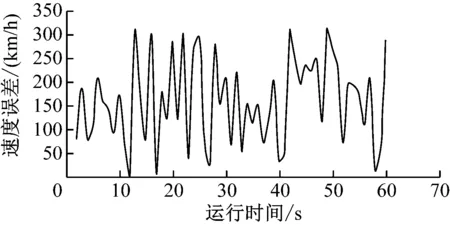
图11 车辆在雨或雪工况时两种算法速度差
4 结语
本文采用基于卡尔曼滤波算法的数据融合技术,充分利用多种不同工作性质的速度检测数据,在线调整算法中各参数的权重,实现对轨道客车速度信息的最优估计。仿真验证结果表明,该技术能够得到真实可靠的轨道客车速度信息。
