基于层叠模型组合煤岩体动态力学本构模型

2019-03-27解北京

煤炭学报 2019年2期

解北京，严正

(中国矿业大学(北京) 资源与安全工程学院，北京 100083)

近年来我国煤炭产量日益增大，煤炭开采深度日益加深，在深部开采条件下，地应力、瓦斯压力显著增大，地质赋存渐趋复杂，冲击地压、煤与瓦斯突出等煤岩动力灾害现象势必增多。然而煤层并非单独存在于地下，而是以煤岩互层的形式赋存。对工作面多种回采方式的研究表明，开采过程中煤体本身破坏的同时，邻近顶底板岩体也会发生损坏，进而产生煤岩互层的整体失稳破坏，因此开采过程需考虑岩层与煤层之间的相互作用[1]。前人对组合煤岩力学特征研究主要集中在静载荷或缓慢加载条件下[2-7]，对冲击载荷下组合煤岩的动态力学特性研究尚未深入开展。本文以矿井实际冲击地压作用的煤岩组合结构体为研究对象，通过实验研究组合煤岩试样瞬间冲击破坏动力学特性，为进一步认识冲击地压等煤岩动力灾害的发生机理和煤岩动力灾害的监测预警提供实验依据，对煤矿安全生产有重要的意义。

煤岩组合体即不同厚度、岩性的煤层与顶板、底板组合构成的结构体，它是冲击地压等煤岩动力灾害直接发生和破坏的结构体[2]。近年来，国内外学者对于煤岩组合本身及其力学特性进行了研究，常采用数值模拟或实验室实验方法，研究组合煤岩的破坏失稳特征，从而掌握“顶板-煤层-底板”之间的相互作用下采动诱发冲击地压的机理和规律[3]。张泽天等[4]在组合方式对煤岩组合体力学特性和破坏特征影响的试验研究中发现，组合体试件破坏主要集中在其煤体部分，而与组合和加载接触方式无关。左建平等[5]对不同煤岩组合体力学特性差异及冲击倾向性分析，认为煤岩组合体的破坏强度及弹性模量与单体煤样相比均有一定程度的提高。宫凤强等[6]对组合煤岩进行4种不同量级下的低加载率单轴压缩试验，得出随着加载率的提高，煤岩组合体的承载失效结构由煤体转化为煤岩组合体，并存在明显的临界加载率现象的结论。王晨等[7]研究了煤体-夹矸-煤体的组合煤岩试样在动静载作用下的变形破坏特征和冲击失稳机理，发现夹矸组合煤岩中随着夹矸厚度和夹矸倾角的增大，组合煤岩的强度会降低。此外，有学者对煤岩组合体各部分的相对高度变化以及接触面倾角对组合体单轴力学特性、破坏特征、冲击倾向性和电磁辐射信号的影响也进行了数值模拟和试验研究[8-10]。可见，组合体试件的各项性质均有别于单体试件，其动态破坏力学特性需要综合考虑各组成部分本身性质、组合方式及相互作用对组合体整体力学性质的影响。

考虑到动载荷下煤岩体的破坏特征与静载下差异较大，在分析此类冲击破坏问题时应采用动态本构模型。于亚伦[11]早在1951年针对岩石动态力学性能提出了过应力模型，1974年LINDHOLM US[12]完善了过应力模型。郑永来和夏颂佑[13]提出了黏弹性连续损伤本构模型。针对煤体，单仁亮等[14-15]提出了时效损伤模型、线性黏弹性模型。付玉凯等[16]提出了损伤体-黏弹性本构模型。目前，材料在动载荷作用下的应变率相关性和损伤弱化已是普遍认可的研究结论。

实验利用中国矿业大学(北京)深部开采国家重点实验室φ75 mm分离式霍普金森压杆(SHPB)试验装置，获得了不同应变率和组合比煤岩体的动态破坏应力应变曲线，基于层叠模型理论建立了组合煤岩动态力学本构模型，利用数值拟合确定模型中的各个参数取值范围，并分析中应变率冲击加载下组合煤岩动态破坏特性。

1 SHPB测试实验原理

1.1 SHPB实验系统及装置

组合煤岩动态冲击实验利用中国矿业大学(北京)的SHPB试验装置完成，SHPB装置由撞击杆(子弹)、输入杆和输出杆组成，被测试样夹在输入杆和输出杆之间，典型的SHPB实验系统、原理、实物如图1～3所示。

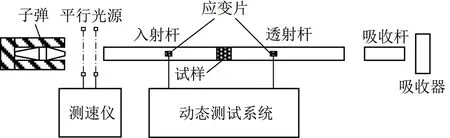
图1 SHPB实验系统Fig.1 SHPB experimental system

图2 SHPB实验原理Fig.2 Principles of SHPB experiment

图3 SHPB测试系统实物Fig.3 Physical map of the SHPB test system

本实验采用特制的纺锤形子弹总长540 mm，直径为75 mm，锥段比为 310∶100∶130 的异型双锥纺锤体子弹[17]，输入杆和输出杆的直径为75 mm，长度为2 000 mm，材质均为钢杆，弹性模量均为206 GPa，将半导体应变片贴在输入杆和输出杆靠近试件端部位置，并且呈对称布置。

SHPB实验的基本原理是细长杆中弹性应力波的传播理论，该理论建立在2个基本假定的基础上，即一维假定(又称平面假定)和应力均匀假定。一维假定认为应力波在细长杆中的传播过程中，弹性杆中的每个横截面始终保持为平面状态;应力均匀假定认为应力波在试件中反复传播3～4个来回，试件中的应力处处相等，即得到如下简化计算公式[18]:

(1)

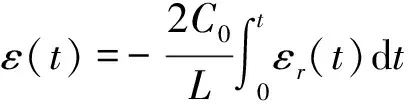
(2)

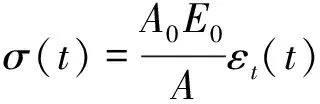
(3)

式中，C0为压杆中弹性波波速;E0为压杆材质弹性模量;A0，L分别为试件横截面积和长度，由于实验煤样在冲击速度为4.5 m/s左右时已破碎，所以本实验子弹的冲击速度控制在4.590～8.791 m/s。

1.2 煤岩组合制作

试验所用组合煤岩试件均由大块煤体和岩体加工而成，每个试样端面和圆周都进行磨床精密加工打磨，两端不平行度小于0.02 mm，圆周与端面的不垂直度小于0.02 mm[19]。实验共计22个“顶板—煤层—底板”组合煤岩试样，其高度比分别为1∶1∶1(MY1-MY5),2∶1∶1(MY7-MY12),1∶1∶2(MY13-MY18),1∶2∶1(MY19-MY23)。为了尽量减少试件的惯性效应和满足内部应力均匀化假设[20]，根据DAVIES和HUNTER[21]所推荐的最佳长径比计算公式，将煤岩样制成直径D=75 mm，长L=40 mm，L/D=8/15的圆柱试样。实验时为了减少界面摩擦效应，在弹性杆与试件界面间涂抹凡士林润滑[22]。实验组合煤岩试样如图4所示。

图4 实验组合煤岩试样Fig.4 Experimental coal-rock combination sample

2 不同组合比煤岩冲击破坏力学特征

本实验中钢质压杆的弹性模量E0=206 GPa、波速C0=5 060 m/s、横截面积A=A0=1 406.25π mm2，试件的横截面积As为1 406.25π mm2，厚度L0为40 mm。共完成了22次冲击压缩，冲击速度为4.590～8.791 m/s，对所有的信号进行去噪处理，用式(1)～(3)计算，最终获得动态力学特性曲线。具体实验数据见表1。

表1实验数据统计
Table1Effectivenumberstatistic

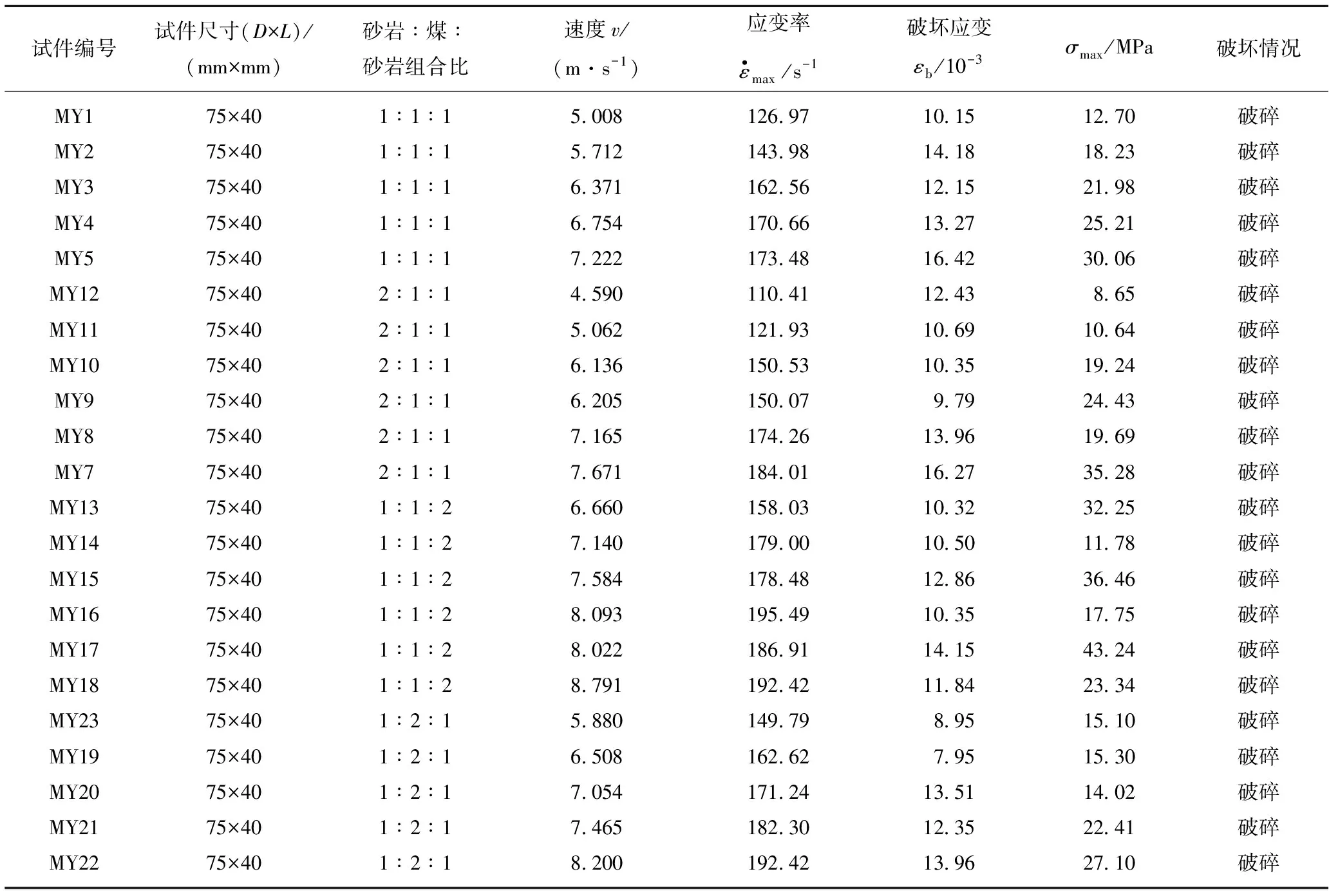
试件编号试件尺寸(D×L)/(mm×mm)砂岩∶煤∶砂岩组合比速度v/(m·s-1)应变率ε·max/s-1破坏应变εb/10-3σmax/MPa破坏情况MY175×401∶1∶15.008126.9710.1512.70破碎MY275×401∶1∶15.712143.9814.1818.23破碎MY375×401∶1∶16.371162.5612.1521.98破碎MY475×401∶1∶16.754170.6613.2725.21破碎MY575×401∶1∶17.222173.4816.4230.06破碎MY1275×402∶1∶14.590110.4112.438.65破碎MY1175×402∶1∶15.062121.9310.6910.64破碎MY1075×402∶1∶16.136150.5310.3519.24破碎MY975×402∶1∶16.205150.079.7924.43破碎MY875×402∶1∶17.165174.2613.9619.69破碎MY775×402∶1∶17.671184.0116.2735.28破碎MY1375×401∶1∶26.660158.0310.3232.25破碎MY1475×401∶1∶27.140179.0010.5011.78破碎MY1575×401∶1∶27.584178.4812.8636.46破碎MY1675×401∶1∶28.093195.4910.3517.75破碎MY1775×401∶1∶28.022186.9114.1543.24破碎MY1875×401∶1∶28.791192.4211.8423.34破碎MY2375×401∶2∶15.880149.798.9515.10破碎MY1975×401∶2∶16.508162.627.9515.30破碎MY2075×401∶2∶17.054171.2413.5114.02破碎MY2175×401∶2∶17.465182.3012.3522.41破碎MY2275×401∶2∶18.200192.4213.9627.10破碎

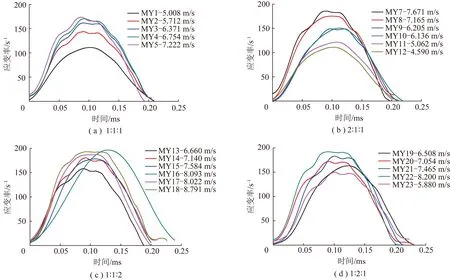
图5 煤岩样动态冲击应变率时程曲线Fig.5 Dynamic impact strain rate time history curves of coal-rock combination sample

图6 煤岩体动态应力应变曲线Fig.6 Dynamic stress-strain curves of coal-rock combination sample

2.1 实测煤岩样动态冲击应变率时程曲线

通过不同冲击速率实现试样的不同应变率加载，可以得到组合煤岩试件的应变率曲线，动载应变率时程曲线如图5所示。

由图5可以看出，组合煤岩试样的冲击应变率随着子弹冲击速率增大而增大，组合煤岩试件加载过程中应变率可分为增大、恒定和减小3个阶段，不同组合比组合煤岩试件的冲击应变率时程均为0.2 ms左右，并且与冲击速度大小无关。0～10 ms为应变率上升阶段，子弹冲击速率越大，应变率的增加速率越大;10～14 ms为应变率恒定阶段，子弹冲击速率越大，恒定应变率越大;0.14～0.20 ms为应变率下降阶段，虽然该阶段加载速度降低，但仍为加载过程。

2.2 煤岩试样冲击破坏应力-应变曲线特征

根据表1得到数据，对所有的信号进行去噪处理后[23]，利用式(1)～(3)计算，最终获得动态力学特性曲线如图6所示。

由图6可以看出，组合煤岩的动态应力应变曲线与煤的动态应力应变曲线特征类似[16,24]，与岩石的动态应力应变曲线明显不同[25-26]。岩石的应力应变在最大值前一般具有跃进特性，具有明显的应变硬化特性，并且岩石的应力应变曲线在第1个极大值之前基本是一条直线，不同速率下偏离也不大，能够很好的重叠，一般认为这个阶段岩石具有线弹性。对于组合煤岩体，在最大值之前，组合煤岩体的动态应力应变曲线呈现出很明显的非线性，这种特征与煤的动态应力应变曲线类似。

对于组合比为1∶1∶1煤岩，其应力应变曲线有较长的弹性阶段和较短的塑性变形阶段，其屈服强度随应变率的增大而增大，弹性模量随应变率的增大而增大，具有较好的规律性;对于组合比为2∶1∶1煤岩，中应变率下其应力应变曲线有较长的弹性阶段和较短的塑性变形阶段，低应变率下其应力应变曲线有较短的弹性阶段和较长的塑性变形阶段，除了冲击速率为7.165 m/s外，其他冲击速率屈服强度随应变率的增大而增大;对于组合比为1∶1∶2煤岩，中应变率下其应力应变曲线有较长的弹性阶段和较短的塑性变形阶段，低应变率下其应力应变曲线有较短的弹性阶段和较长的塑性变形阶段，当冲击速度为6.660 m/s和8.093 m/s时，曲线表现出了岩石的跃进性，具有明显的应变硬化特性，曲线上升到第一个极大值后，应力随之减小，后又增大，呈现跃进性，跃进4～5次，试样完全破坏，且塑性变形最强;对于组合比为1∶2∶1煤岩，原煤所占比例高，跟其他组合比煤岩相比，其屈服强度小，屈服强度随应变率的增大而增大，其应力应变曲线有短长的弹性阶段和较长的塑性变形阶段。

综上所述，煤岩组合体的动态应力应变曲线在最大值之前呈现出很明显的非线性，不同组合比煤岩的弹性阶段和塑性阶段持续时间不同，组合比中原煤占比高，其屈服强度小，组合煤岩屈服强度基本满足随应变率的增大而增大的规律。组合煤岩的动态应力应变曲线与岩石和煤的动态应力应变曲线有所不同。因此，为了进一步深入研究组合煤岩动态应力应变特性，需要建立适合组合煤岩冲击荷载下的动态本构模型。

3 动态本构模型的确立及验证

3.1 动态本构模型的建立

从组合煤岩体的动态应力应变曲线可以看出，煤岩体在冲击荷载作用下，表现出了非线性、塑性流动性、损伤失效以及应变率相关性等综合相应的力学特性，传统的线弹性阶段却表现出非线性。在中低应变率条件下，材料呈现显著的强化和脆化现象，应变率强化效应明显，所以对于煤岩体动态本构关系的研究必须考虑应变率效应。此外，煤岩体内部存在大量微裂纹和微孔洞，在冲击载荷作用下，损伤演化显著，尤其是在中髙应变率条件下。因此，在研究煤岩体的动态本构关系时，应充分考虑损伤效应的影响。

层叠模型的各个叠层厚度和材料特性均可不同，各个叠层的节点都是一个节点，因此在每一层上的应变都应相同[27]。针对岩石在中应变率下，表现出了弹塑性、损伤失效以及应变率相关性等综合相应特性，建立符合连续介质基本原理的损伤弹塑性动态本构模型;针对煤体，在付玉凯[16]提出的损伤体-黏弹性本构模型基础上，建立中应变率下煤体损伤体黏弹性本构模型。笔者借鉴前人学者的研究成果以及对实验曲线特征的分析，将岩石的损伤弹塑性动态本构模型和煤体的损伤体黏弹性本构模型进行层叠，建立了7参数层叠本构模型，该模型充分考虑了组合煤岩体在动态破坏中的应变率相关性和损伤特性，并能够与突变理论较好的结合。建立本构模型如图7所示。

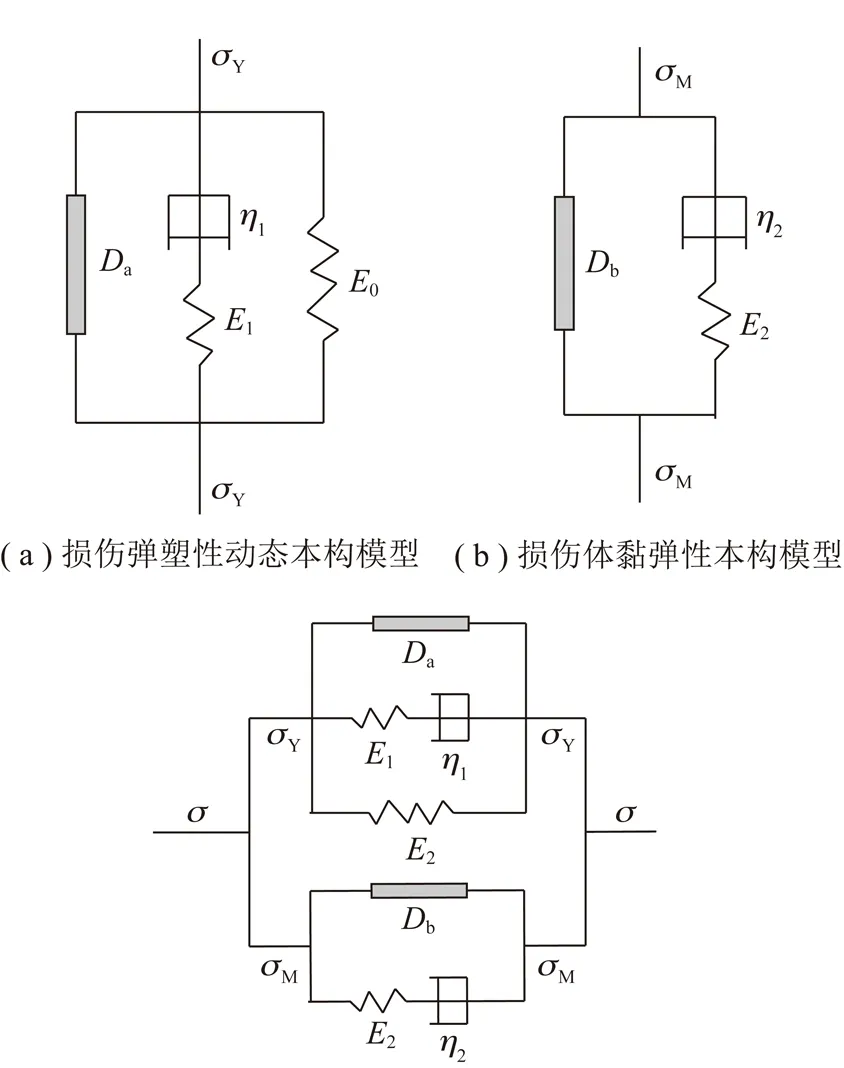
图7 7参数层叠本构模型Fig.7 7 parameter laminated constitutive model

岩石本构模型损伤体Da在损伤之前是线弹性的，平均弹性模量为EY，强度服从参数为(m，α)的weibull分布。其概率密度φ(εa)损伤参数D以及本构关系σ-ε可以分别由下式求出:

(4)

(5)

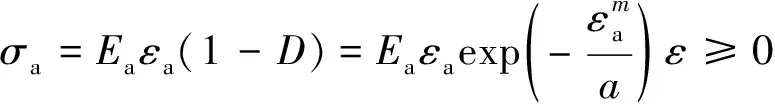
(6)

模型中麦克斯韦元件和胡克元件表示岩石的中应变率弹塑性响应。其本构方程为

(7)

σ2=E0ε

(8)

则损伤弹塑性动态本构模型的本构关系,即

(9)

煤体本构模型损伤体Db在损伤之前是黏弹性的，平均弹性模量为EM，强度服从参数为(n，b)的weibull分布。其概率密度φ(εb)损伤参数D以及本构关系σ-ε可以分别由下式求出:

(10)

(11)

(12)

模型中麦克斯韦元件表示煤体的中应变率弹塑性响应。其本构方程为

(13)

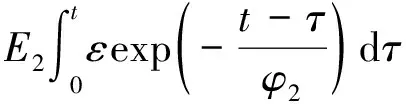
(14)

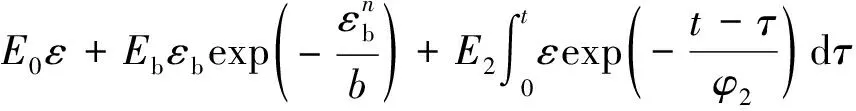
(15)

式中,Ea，Eb，E0，E1，E2均为弹性模量常数;φ1，φ2为松弛时间;岩石本构中各元件的应变等于煤体本构中各元件的应变，各个系数由数据拟合确定。

3.2 动态本构模型的实验验证

对不同组合比煤岩在不同冲击载荷下应力应变曲线进行拟合，由于参数过多，把其中参数m，α，φ1，φ2进行试算，m，n取值为1，α，b一般位于曲线峰值所对应的应变附近，其它参数进行最优化计算，部分拟合结果和拟合参数如图8和表2所示。

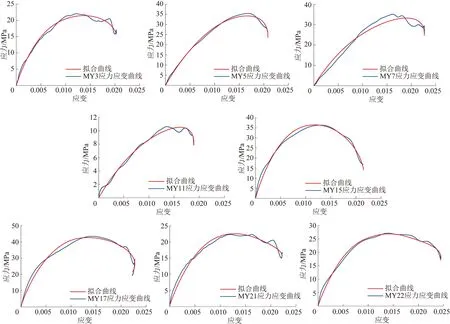
图8 不同组合比试样的实验和拟合动态应力-应变曲线Fig.8 Experimental and fitting dynamic stress-strain curves of specimens with different combination ratios

从图8可以看出，组合煤岩试样的拟合曲线与实验曲线无论是前期还是后期都具有较好的一致性，说明7参数层叠本构模型和所确定的参数是适合于研究动态加载煤岩体的。一维应力波在多层材料中传播时，当到达两种波阻抗不同介质的交界面时，就会在交界面处发生波的反射和透射，对于有限厚度的介质，试样在达到应力均匀前反射的次数不仅仅决定于外加载荷，而且与相邻介质的力学性质和几何尺寸有关[28]。对于相同组合比煤岩试样，当外加载荷改变时，形成不同破坏程度的损伤区，对于应力波的衰减程度不同，造成不同的破坏形态;对于不同组合比煤岩试样，由于介质几何尺寸的差异，入射拉伸波与反射拉伸波叠加形成较强的拉伸集中区形态不同，造成不同的破坏形态。典型的部分实验结果如图9所示，相同组合比组合煤岩，随着冲击速度的增大，组合煤岩破坏越严重;不同组合比组合煤岩，冲击速度相差不大情况下，例如MY3,MY9,MY13,MY19组合煤岩，应力波达到不同波阻抗材料的界面，发生反射和透射，由于砂岩和煤体的比例不同，入射拉伸波与反射拉伸波叠加形成的较强的拉伸集中区形态不同，形成不同的破坏形态。

表2部分应力应变曲线拟合参数
Table2Partialfittingparametersofstress-straincurve

煤岩体Ea/GPaEb/GPaE0/GPaE1/GPaE2/GPaαbφ1/s-1φ2/s-1RMY31.881.870.004 40.003 700.012 20.012 10.34260.994 9MY59.329.310.004 50.002 500.016 80.016 40.57480.997 2MY77.287.260.012 50.002 200.016 20.016 10.61520.988 8MY111.661.650.002 50.000 800.010 70.010 60.54410.990 4MY159.049.010.027 90.007 300.012 90.012 30.59450.991 7MY175.465.440.010 60.007 900.014 20.013 70.62530.989 0MY212.212.2000.004 90.025 30.014 00.013 90.74620.994 0MY223.573.5600.003 20.007 10.008 80.008 50.22130.992 3

图9 实验结果Fig.9 Experimental results

从拟合参数可以看出，反映煤岩体损伤弹性模量Ea,Eb远远大于反映弹塑性弹性模量E1,E2，说明在中应变率冲击载荷作用下，组合煤岩体损伤软化效应超过应变率强化效应成为主导因素;当冲击速率较小时，煤岩体损伤弹性模量Ea，Eb较小，当冲击速率较大时，Ea，Eb急剧变大，表现为应变强化的响应性质[29];反映岩石的Maxwell体的松弛时间φ1数值较小，反映煤的Maxwell体的松弛时间φ2数值较大，那么就会积累过多的能量，导致煤体比岩石破坏程度大，不受组合方式影响，如图9所示。从模拟的数值结果来看，煤岩组合比为1∶1∶1,1∶1∶2和2∶1∶1时，煤体占比较小，反映煤的Maxwell体的弹性模量E2为0，煤岩组合比为1∶2∶1时，砂岩占比小，反映岩石的胡克元件的弹性模量E0为0;对于组合比为1∶1∶1和1∶1∶2,2∶1∶1组合煤岩试件，1∶1∶1组合煤岩试件的砂岩占比较小，反映岩石的胡克元件的弹性模量E0略小于1∶1∶2和2∶1∶1组合煤岩试件;对于1∶1∶2和2∶1∶1组合煤岩试件，模拟结果未体现出较大的差异性，可能原因是组合煤岩尺寸太小，导致拟合参数规律不明显。不同组合比试件通过建立的七参数本构拟合参数的结果体现出组合尺寸的差异性。

同时应该强调的是由于组合煤岩冲击破坏SHPB实验条件有限，并未考虑围岩影响，围压下的组合煤岩动态破坏特性有待利用实验和数值模拟手段进一步研究。