基于光谱技术的Bipls算法结合CARS算法的苹果可溶性固形物含量检测
2019-03-26饶利波陈晓燕
饶利波, 陈晓燕, 庞 涛
(1. 四川农业大学 机电学院, 四川 雅安 625014; 2. 四川农业大学 信息工程学院, 四川 雅安 625014;3. 四川农业大学 农业信息工程四川省重点实验室, 四川 雅安 625014)
1 引 言
苹果是水果市场上最受消费者欢迎的水果之一,而可溶性固形物含量(Soluble solids content,SSC)是影响苹果内部品质的重要属性,因此苹果SSC 的检测对国民生活拥有重大意义。光谱技术所含信息丰富、方便快捷、无损伤性使其成为当下最热门的检测技术之一[1]。
在实验中光谱数据的巨大数据量使计算过程复杂且费时,因此特征变量的选取方法成为光谱分析领域的研究重点。常用的变量选择方法有连续投影法(Successive projections algorithm,SPA)[2-3]、无信息变量消除法(Uniformation varible elimination,UVE)[4]、竞争自适应加权重采样法(Competitive adaptive reweighted sampling,CARS)[5-7]和Random Frog[8]算法等。洪涯等(2010)在检测砂糖橘酸度中利用SPA算法提取13个有效变量,所得pls线性模型预测相关系数Rp=0.825 277。Dong and Guoetal.(2016) 在苹果SSC检测研究中利用UVE提取122个有效变量,pls模型相关系数Rc和Rp分别为0.744和0.863。詹白勺等(2014)利用CARS算法测定库尔勒香梨SSC,以提取的42个有效变量间非线性LS-SVM模型决定系数r2=0.851 2。本次研究采用后向区间偏最小二乘法(Backward interval partial least squares,Bipls)[9-10]结合CARS算法进行变量选择,Bipls能在全光谱范围内选取到与待测成分最相关的光谱范围区间,CARS算法能根据每个波长对模型的重要性提取出最关键的波长。通过所选关键变量建立预测模型并将模型预测精度与Bipls-PLS模型和Bipls-SPA-PLS模型相比较,获得了更好的预测结果。
2 实 验
2.1 样本
所用实验样品皆采购于雅安市水果市场,共计126个。将苹果无损伤运回实验室后用蒸馏水洗净,贴好标签,在实验室室温25 ℃和正常湿度条件下静置24 h。所有样本分为训练集和测试集两组,其中训练集90个,测试集36个。
2.2 光谱数据的获取
反射光谱的采集采用GaiaSorter高光谱分选仪(Zolix Instruments Co.Ltd,China),该仪器光谱范围为400~1 000 nm,光谱分辨率是2.8 nm,共采集256个波段。图像在采集前,为了使初期采集环境同后期环境温度和光源强度一致,先启动高光谱分选仪预热30 min,并将标准白板的高度调至与苹果样品同一焦面上。采集时,电机控制传输带前进速度为0.5 cm/s,回退速度为1 cm/s,曝光时间为23 ms,增益为1,如图1所示。

图1 光谱分选仪结构图
2.3 可溶性固形物含量的测定
苹果可溶性固形物的理化值测定采用型号为LB20T的糖度折射仪来完成。测定前用蒸馏水将折射仪的检测棱境洗净,将标定好的苹果感兴趣区域处的果皮削去,切取2~3 mm果肉挤出适量果汁置于折射仪的检测棱镜上,读出该样品SSC理化值示数。为减小测定结果的随机性,每个样本重复以上操作3次,取其平均值作为该样本的测量结果。
3 结果与讨论
3.1 样本划分
为了提高模型的预测精度,以及确保用于构建预测模型的训练集样本所含信息的代表性。利用K-S(Kennard-Stone)[11]算法基于样本间的欧氏距离将126个样本划分为训练集和测试集两组。K-S算法划分的训练集与测试集的SSC统计值如表1所示。

表1 训练集和预测集的可溶性固形物含量统计表
3.2 数据预处理
受实验环境的制约,采集的光谱中会掺杂一些随机噪声,而平滑可以在保留光谱轮廓前提下消除噪声,因此实验选用卷积平滑法(Savitzky-Golay )[12-13]来去除噪声。经过实验研究发现,S-G平滑去燥时将移动窗口设置为15,用于拟合的多项式次数为3,导数阶数设置为0,效果较好。经过S-G平滑后的光谱图像如图2所示。
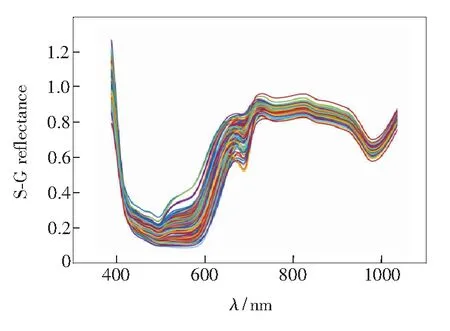
图2 S-G处理后的光谱图像
为了进一步滤除光谱中与待测成分无关的信息,实验在S-G平滑的基础上利用直接正交信号校正(DOSC)[14-15]对光谱数据进行二次预处理。DOSC通过将光谱矩阵与待测浓度矩阵正交,在不损害数据结构特性的前提下滤除与SSC无关的信息,将最相关的信息用于预测模型的构建,进而提高模型的预测精度。算法步骤中的权重向量的计算公式如下:
t=Xr,
(1)
r=X+t,
(2)
其中t是得分向量,X+是X的Moore-Penrose逆,而Moore-Penrose逆的容差是1E-6。容差值是影响X-计算的一个关键因素,当容差值是1E-6时即为完全正交性约束状况,公式(1)中t的拟合过程会将X中不稳定的方向也囊括在内,导致t的拟合过程出现过度拟合现象,致使DOSC的滤除效果不明显。因此,实验中选用容差为1E-3计算出来的广义逆X-来代替X的Moore-Penrose逆且DOSC成分数设置为2。 DOSC处理后的光谱图像如图3所示。

图3 DOSC处理后的光谱图像
从图中可以看出无论是训练集还是校正集,相较于未经过处理的图像,DOSC处理后的光谱图像线条更加紧密,凸起的波峰也更加集中反映了数据与待测成分的相关性得到了良好的提升。
3.3 特征变量的提取
反向区间偏最小二乘法(Bipls)基本原理是将全光谱等距离地划分为N个子区间,与区间偏最小二乘法(ipls)对每个子区间进行pls回归不同,Bipls是对全光谱建立pls线性回归模型。在此基础上每次剔除一个子区间,然后再对剩下的所有子区间进行pls回归,而剔除的那个子区间则是每次回归模型所有子区间中性能最差、剔除后使得模型评价RMSE最小的那个。依此类推,剔除到只剩下一个子区间为止。实验中为了对子区间的划分做优化选择,我们将全光谱划分了10~25个子区间(pls回归中最大主成分数设置为10,若区间数大于25,则子区间变量数少于主成分数),再以交互验证法选出均方根误差(RMSECV)最小值所对应的区间数。如表2所示,当所划区间数为23时,RMSECV最小为0.545 1。
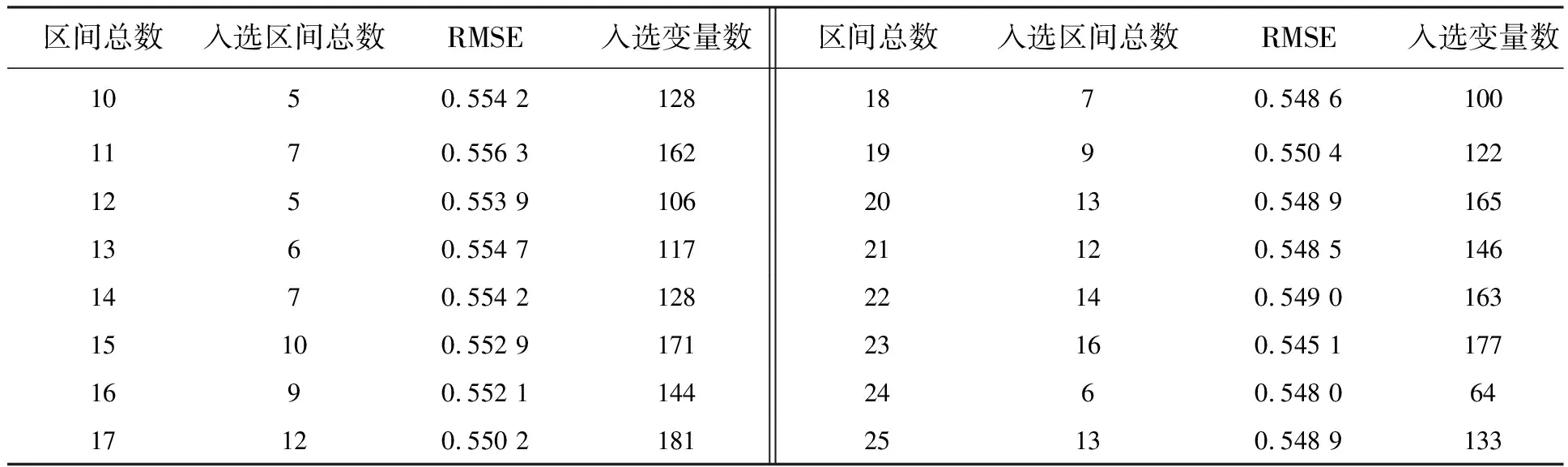
表2 不同区间总数划分结果
由表2确定将全光谱等距离划分为23个子区间后,开始将所有子区间联合建模,每一次剔除表现最差的子区间。表3所示为23个子区间的建模结果,当剔除掉第22个子区间时对剩下的16个子区间进行pls回归,所得均方根误差(RMSE)最小为0.545 1。往后再依次剔除其他子区间后发现RMSE值又开始逐渐变大,说明这时所去掉的子区间包含着对建模较为有用的信息。此时建立的pls模型相关系数r=0.864 6,主因子数为4,Bias为0.011 4,则所选子区间为3,5,6,7,8,9,13,14,15,16,17,18,19,20,21,23等16个子区间,对应的波长区间为448.1~476.1 nm、506.6~643.7 nm、730.1~979.1 nm、1 009.6~1 035.0 nm,总计177个波段。如图4所示。

表3 子区间优选结果

图4 Bipls优选子区间
经过Bipls算法的初步选取,我们得到了光谱范围内与苹果可溶性固形物含量最相关的波长区间,共含177个波段,波段数量明显下降。但相邻波段间仍存在很严重的共线性问题,此外数据的冗余问题也并未得到很好的解决。因此,实验以Bipls的初步选取结果为基础,利用竞争自适应重加权采样算法(CARS)进行最优化的变量选取。CARS算法是模仿基于达尔文进化论“适者生存”原则提出的一种关键变量选择方法。
CARS通过对光谱数据建立pls模型求取每个变量的权重ω,权重值越大则代表该变量对模型建立的贡献越大,被选取的概率越大。如公式(3)和(4)所示:
T=XW,
(3)
y=Tc+e=XWc+e=Xb+e,
(4)
其中X是m行p列的光谱矩阵,T是X的得分矩阵,是X与W的线性组合,W是组合系数,c表示y与T建立pls模型的回归系数向量,e是误差向量,式中b=Wc,是一个p维列向量。权重ω被定义为:
(5)
在CARS运行时,首先要设定好Monte-Carlo 采样次数N,以期在循环运行N次后获得N个变量子集,通过比较每个变量子集的交互验证均方根误差(RMSECV),选择RMSECV值最小的变量子集为最优变量子集。在CARS的每次运行过程中,无信息变量或低信息变量的去除主要分两个步骤,分别是指数衰减函数(EDF)去除和自适应重加权采样(ARS)去除。每次EDF运行中被保留变量所占比例为:
ri=ae-ki,
(6)
其中a与k作为两个常数的决定条件为:(1)第一次运行时,模型建立所用波段为全波段,所以r1=1;(2)第N次运行时,模型建立所用波段只有2个,所以rN=2/p。a与k被定义为:

(7)
(8)
选择时,先用EDF强力快速移除一些权重较小的变量,然后ARS再从剩下的p×ri个变量中按照“适者生存”原则以竞争的方式选出新的变量子集,再用交互验证法求出新子集的均方根误差(RMSECV),并进入下一个循环。

图5 CARS运行结果
图5(a)所示为指数衰减函数的筛选过程,Monte-Carlo 采样次数在1~20期间时,变量数量随着采样次数迅速下降为“快速选择”阶段;20次采样以后变量数下降速度趋于平缓,为“精选选择”阶段。图5(b)为随着Monte-Carlo 采样次数的增加各子区间的RMSECV值的变化,前期随着采样次数的循环运行,所生成的子区间由于移除了大量无信息变量的缘故RMSECV的值随之缓缓减小,而后在运行后期陡然增大的原因是选择过度,移除了富含信息的关键变量,导致模型性能下降。图5(b)中后期增大呈两极阶梯状,如图5(b)中S1、S2节点与图5(c)对应的是两个变量的回归系数路径趋近0的终点,说明这两个变量就是被过度选择所移除的关键变量。图5(c)是每个变量在50次采样运行中的回归系数路径图,星号垂直线所对应的是图5(b)中RMSECV值最小的子区间,该子区间即为CARS最终所选最优子区间,包含449.6,512.9,544.8,547.2,594.3,596.8,928.2 nm等7个波长。
3.4 PLS建模结果
以CARS所选7个关键变量为基础,建立PLS线性回归模型。对PLS建模而言,最佳主因子数的选取具有非常重要的意义,主因子数偏少容易导致模型预测结果欠拟合,主因子数偏多则导致模型预测结果过度拟合。实验采用留一交叉验证法确定最佳主因子数,计算所得y的最小预测误差平方和PRESS等于17.000 2,所对应最佳主因子数为3。模型评价为训练集相关系数Rc=0.906 2,训练集均方根误差RMSEC为0.482 2;测试集相关系数Rp=0.871 6,测试集均方根误差RMSEP为0.614 0。为了与Bipls-CARS-PLS模型性能相比较,通过实验分别对Bipls-PLS模型和Bipls-SPA-PLS模型也做出了模型评价,其比较结果如表4所示。

表4 不同模型效果比较
直接对Bipls筛选过的子区间变量建模,虽然训练集与测试集的模型评价分别为Rc=0.921 7和Rp=0.958 8,但是建模所用变量高达177个而且RMSEC和RMSEP之间差值过大。而Bipls-SPA-PLS模型建模所用变量数量仅为2个,在解决数据的共线性问题上性能优异,但也可能遗漏了某些关键变量,因而模型的训练集和测试集的相关系数与Bipls-CARS-PLS相比略微小一些。
4 结 论
利用高光谱技术对苹果的可溶性固形物含量的无损检测过程中,实验采用了Bipls、Bipls-SPA和Bipls-CARS这3种关键变量选取方法,结合PLS建模方法对其所选变量建立预测模型。Bipls-SPA所选变量为2个,模型评价Rc和Rp分别为0.810 9和0.844 9,RMSEC和RMSEP分别为0.681 2和0.641 0。Bipls-CARS最终提取了7个最优变量,模型相关系数Rc和Rp分别为0.904 6和0.871 6,RMSEC和RMSEP分别为0.482 2和0.614 0。与Bipls-SPA相比,Rc和Rp有明显提高,均方根误差RMSEC和RMSEP略微下降。Bipls模型评价Rc和Rp分别为0.921 7和0.958 8,RMSEC和RMSEP分别为0.440 6和0.701 3。虽然预测精度优于Bipls-CARS,但是所用变量为177个,计算成本高,模型构建复杂且RMSEC和RMSEP之间差值过大,模型鲁棒性不足。综合衡量模型预测准确度和稳定性等性能,结果表明Bipls-CARS-PLS模型的检测性能优于Bipls-PLS模型和Bipls-CARS模型。
