厚度误差对THz-TDS的测量不确定度分析

董海龙， 汪家春， 刘瑞煌， 马冬晓， 赵大鹏

(国防科技大学电子对抗学院 脉冲功率激光技术国家重点实验室， 安徽 合肥 230000)

1 引 言

太赫兹(Terahertz,THz)波通常指电磁辐射频率在0.1～10 THz(波长在30 μm～3 mm)范围内的电磁波，具有瞬态性、低能性、相干性、宽带性及强穿透性(对非金属物质、非极性物质)等特性[1-4]。太赫兹时域光谱系统(Terahertz time domain system,THz-TDS)是太赫兹技术的一项重要应用，可通过测量得到材料的光学常数，如折射率、介电常数、吸收系数等，广泛应用于物质鉴定和成分分析领域[5-6]。目前，受设备控制精度、系统噪音以及实验操作、数据处理过程的影响，研究人员在利用THz-TDS进行参数测量过程中会出现或大或小的误差，得到不同的测量结果。如Nakanishi和Reid等在文献中报道，测得水在0.5 THz的折射率分别为2.3和2.05左右，存在较大差异[7-8]。本文以厚度误差对透射式THz-TDS测量固体光学常数的影响进行分析，并通过实验验证了分析模型的有效性，对测量过程及结果分析具有一定的指导意义。

2 基于菲涅尔公式的THz-TDS光学常数提取方法

材料的光学常数是用来表征其宏观光学性质的物理量，一般包括复折射率、介质损耗、电导率、吸收系数等[9-10]。这些参数之间是相互关联的，一般可利用已知的一个或者一组参数计算出其他参数。材料的光学常数不是常数，而是频率的函数。通常，我们用材料的复折射率描述其宏观光学性质，可表示为：

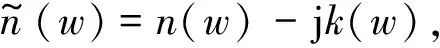
(1)

式中，n(w)为材料的折射率，描述材料的色散情况；k(w)为材料的消光系数，描述材料的损耗；w为角频率。材料的吸收系数α(w)也可以通过消光系数k(w)求得：

(2)

太赫兹时域光谱系统的关键特征是可以有效地测量材料在太赫兹波段下透过系数的振幅和相位，得到材料在太赫兹波段下的物理和化学信息，可用于提取材料在太赫兹波段的光学常数，如介电常数、复折射率等，在半导体材料、电介质材料、生物大分子(如DNA、蛋白质)以及超材料等研究中具有重要作用[11]。

法国的Duvillaret等提出一种基于菲涅尔公式的解析法，利用透射式THz-TDS测量材料的折射率和吸收系数等[12-13]。该方法适用于提取对太赫兹吸收较弱的材料，如非金属、非极性材料等，对强吸收材料并不适用。该方法在进行材料光学常数提取过程中必须满足以下条件：(1)测量表面是平行且光滑的片状样品；(2)待测样品上下表面的介质满足磁各向同性，介质的电磁场响应是线性的，如正常条件下的空气、真空或惰性气体等；(3)测量样品较厚，可忽略多次反射的回波造成的法布里-珀罗震荡。

如图1，入射太赫兹脉冲由介质a进入介质b，并在其间发生透射和反射，由介质b射出介质a。

图1 太赫兹波在样品中的透射与反射

Fig.1 Transmission and reflection of THz wave in the sample

FP(w)，

(3)

(4)

(5)

(6)

3 厚度误差对透射式THz-TDS测量过程的分析与仿真计算

由上节分析可知，利用透射式THz-TDS可直接测量获得材料在太赫兹波段的光学常数。然而，THz-TDS通常由机械装置、光学部件和电子元件等部分组成，各个部分的控制精度、响应误差、系统噪声以及实验操作、数据处理等方面均会影响材料光学常数的准确性。因此，分析THz-TDS测试的不确定度对于准确提取材料光学常数具有重要的意义[14-15]。本文从厚度误差方面研究其对提取材料光学常数准确度的影响，旨在提高后续材料光学常数研究的准确性。

3.1 厚度误差对透射式THz-TDS测量的不确定度分析

图2是透射式THz-TDS的结构图，其光谱分析属于相干分析。来自相同激光光源的一束激光经半透镜后，一束进入发射天线产生太赫兹波，透过样品；另一束激光经过延迟装置进入探测天线，对经过样品的太赫兹波进行数值采样，得到时域光谱。对时域信号进行离散Fourier变换，得到频域光谱。

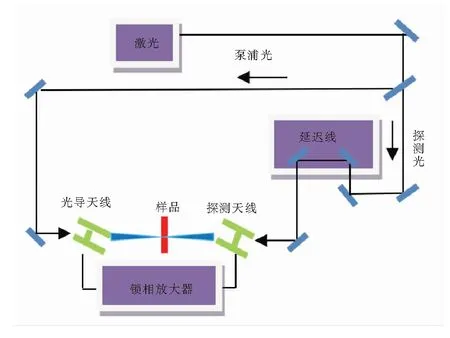
图2 透射式THz-TDS结构图

根据图1，太赫兹脉冲在样品中的传输距离d是样品厚度l和折射角β的函数，其表达式为

(7)

从公式(7)可得传输距离d的方差，表达式如下：

(8)

根据Snell’s 方程，折射角β与入射角θ、空气折射率n0和样品折射率n有关，表达式为

(9)

假设样品的折射率n和空气折射率n0是测量准确的，则入射角的方差表达式为

(10)

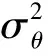
(11)

根据公式(5)和(6)，此时只考虑样品厚度误差对折射率误差的影响。由公式(8)和(11)，样品折射率和消光系数的方差可以简化为：

(12)

(13)

3.2 厚度误差对透射式THz-TDS测量的不确定度模型仿真

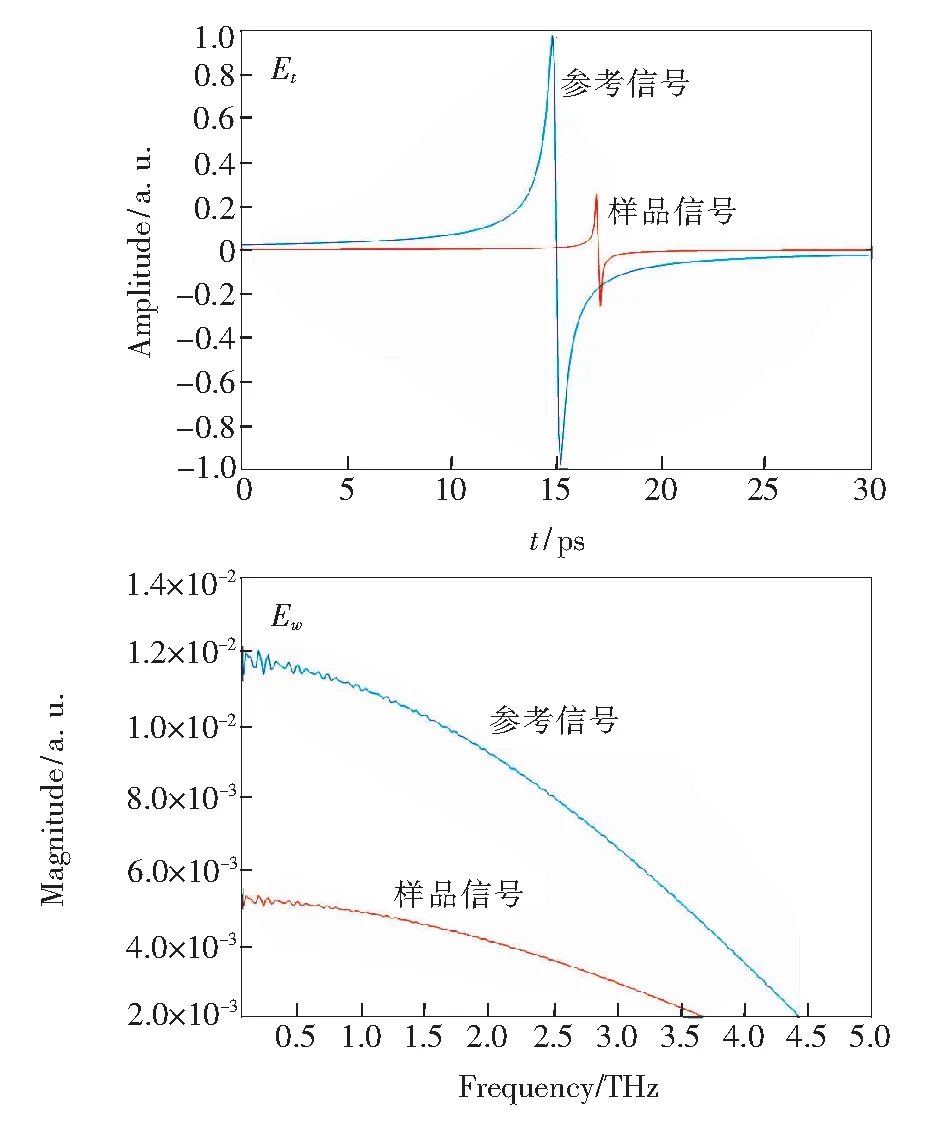
图3 太赫兹时域及频域信号

根据厚度误差对透射式THz-TDS测量的不确定度分析，取样品厚度的标准差σl=5 μm，研究不同频率下由σl对提取样品折射率和消光系数造成的影响。根据公式(12)、(13)，利用MATLAB进行数值仿真，结果如图4所示。

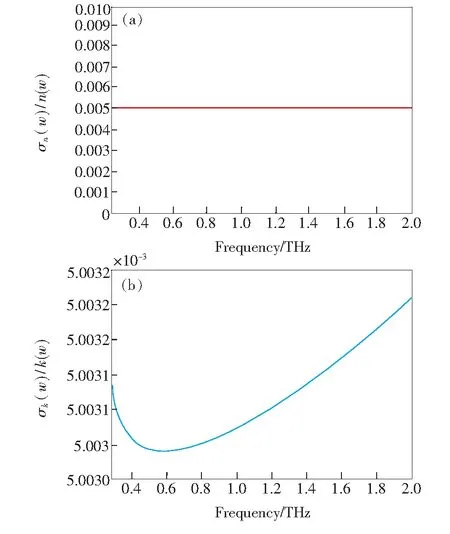
图4 样品厚度误差σl=5 μm对提取光学常数的影响。(a)折射率标准差；(b)样品消光系数标准差。

Fig.4 Standard deviation of optical constants effected byσl=5 μm. (a) Standard deviation of refractive index. (b)Standard deviation of coefficient of light extinction.

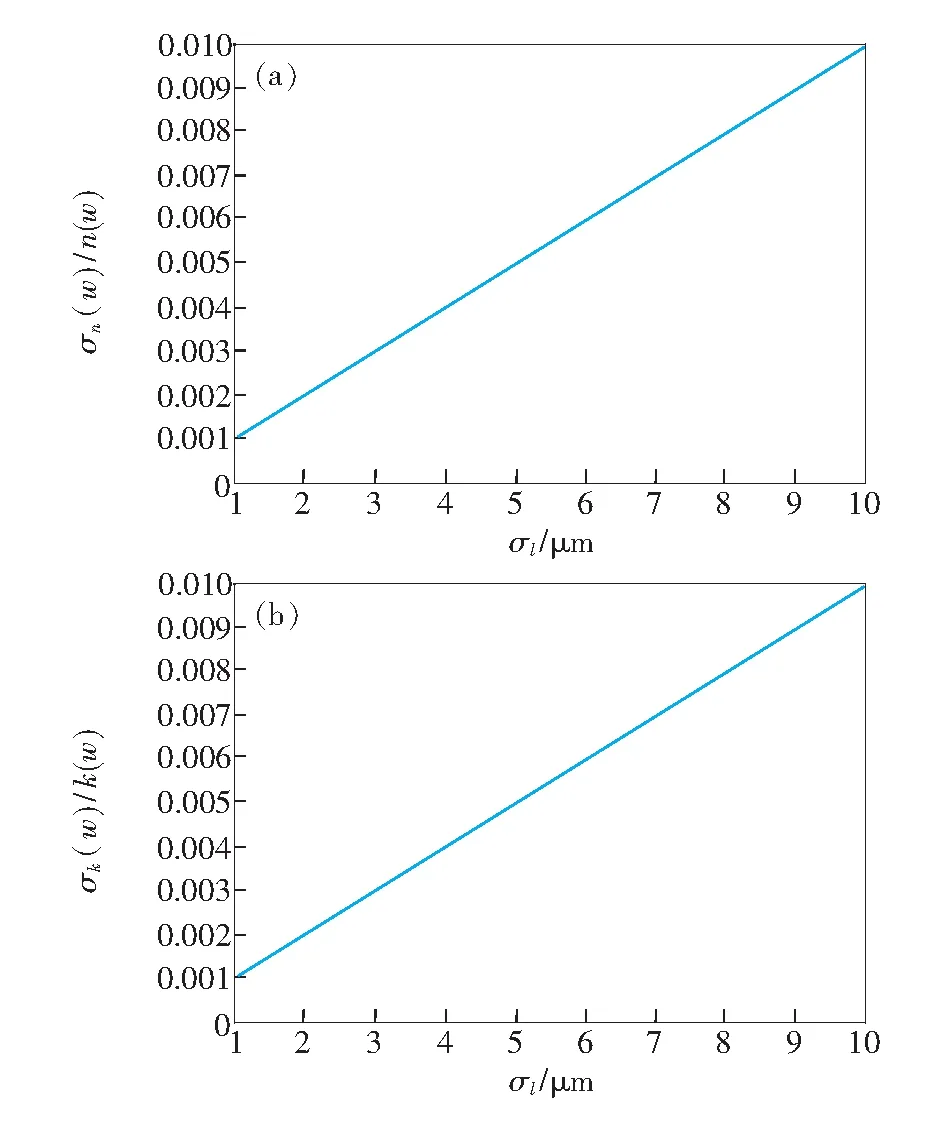
图5 不同样品厚度误差对提取光学常数的影响。(a)折射率标准差;(b)样品消光系数标准差。

Fig.5 Standard deviation of optical constants effected by differertσlfrom 1 to 10 μm. (a) Standard deviation of refractive index. (b) Standard deviation of coefficient of light extinction.

由图4可知，样品光学常数的测量不确定度受样品厚度误差的影响。由图4(a)可发现，在σl一定的情况下，折射率不受频率的影响；在图4(b)中，折射率虽然随频率的变化而变化，但是变化幅度很小，仅为10-7数量级，可认为不受相应误差条件下频率的影响。由两图可知，折射率和消光系数的测量受样品厚度误差的影响几乎相同。

取样品厚度的标准差σl从1～10 μm递增，研究σl对提取样品折射率和消光系数的影响，结果如图5所示。

由图5可知，在样品厚度为1 mm时，样品折射率和消光系数的测量误差随厚度误差的增大而增大。在厚度误差为1 μm时，变化幅度为10-3数量级。当厚度存在10 μm的测量误差时，系统的测量结果将出现10-2数量级的变化幅度。

4 厚度误差对THz-TDS测量实验

上节分析了样品厚度误差对透射式THz-TDS测量固体光学常数的影响情况，并建立了误差对测量结果的影响模型。为了验证模型的有效性，选择硅片为测试样品，进行太赫兹时域光谱测量实验，提取硅片在太赫兹波段的折射率，验证厚度误差对提取样品光学常数不确定度模型的有效性。

4.1 实验准备

硅是常用的半导体材料，主要包括单晶硅、多晶硅以及非晶硅。其中，单晶硅具有完整的点阵结构，在不同的方向上具有不同的性质，是一种性能优良的半导体材料，其纯度高达99.9999%以上。实验选取单晶硅作为样品，有以下几个主要原因：(1)单晶硅具有表面平整光滑、内外表层相互平行的特点，适合用于THz-TDS的实验测量。(2)硅属于非金属物质，反射率较低，适用于透射式THz-TDS的参数提取测量实验；(3)大量实验表明，在远红外波段最透明的半导体材料就是高阻的单晶硅；(4)国内外进行了大量单晶硅材料在太赫兹频段的特性研究，已获得相关的光学特性和参数，可为实验测试结果提供数据支撑[17]。实验样品选取4种不同厚度的P型单抛单晶硅，其表面光滑抛光，用电子数显千分尺对样品厚度进行多次测量，获得平均厚度分别为303，502，710，994 μm。

4.2 实验过程

实验采用TDS-1010飞秒激光THz-TDS进行测量，脉冲光斑尺寸为22 mm(聚焦光束为2.0 mm)，宽度<100 fs，中心波长1 060 nm，系统光谱范围为0.1～5 THz。实验过程中，利用样品夹将单晶硅片垂直立于样品架，使入射太赫兹脉冲垂直入射到样品表面。在测量过程中，采用加充氮气对样品仓中的空气湿度进行控制，利用中央空调对室内温度进行调节。

对每片单晶硅的太赫兹时域光谱信号交替测量5次，获得5次测量的太赫兹时域及频域信号平均值，为提取和分析单晶硅的光学常数提供数据来源。如图6所示，是厚度为303 μm单晶硅样品5次实验测量的时域及频域平均值。图6(a)记录的是在干燥空气中(加充氮气、环境温度为25 ℃)，参考信号(即空气)和厚度为303 μm的单晶硅片样品的太赫兹时域光谱信号，表示经过样品的太赫兹脉冲电场随时间的变化情况。图6(b)是时域信号经过Fourier变换得到的脉冲频域分布。

图6 样品的太赫兹光谱图。(a)太赫兹时域光谱信号；(b)太赫兹频域信号。

Fig.6 Terahertz spectroscopy of sample. (a) Terahertz time-domain spectral signal. (b) Terahertz frequency domain signal.

从图6(a)可以看出，在太赫兹时域光谱中，具有单晶硅片时，时域信号峰值相对于参考信号峰值存在一定的延迟，且信号的峰值强度也存在一定的衰减。峰值出现延迟的原因是样品在太赫兹波段的折射率大于空气的折射率。在探测距离，即发射天线与探测天线位置固定的情况下，样品折射率的增大相当于增大了太赫兹脉冲的光程，而该系统中脉冲的探测属于相干探测，增加的光程需要系统延迟线进行补偿，因此峰值出现了延迟现象。由于样品对太赫兹脉冲存在一定的衰减，故样品信号峰值强度出现一定的衰减。从图6(b)可以看出，样品信号在不同的频率处太赫兹脉冲的衰减过程不同，脉冲信号在样品中的透过率也不一样。利用相关软件，分别代入测量的4块样品的光谱数据和平均厚度，计算获得每块样品在太赫兹波段的折射率，如图7所示。

图7 实验获取样品的折射率

从图7可以看出，4块不同厚度样品的折射率随频率上下波动，且在频率较高处，样品的折射率振荡更大一些，这可能是受测量过程中系统误差影响，如系统噪音、延迟线位置偏差、Fabry-Perot效应引起的反射误差。在频率较高处，如1.5 THz以上(波长200 μm)，脉冲信号弱，信噪比低，对测量结果产生更大的振荡。

利用相关软件，可获得样品在太赫兹波段下的平均折射率。根据公式(12)，只考虑厚度误差对提取样品折射率误差的影响，计算样品折射率的标准差。利用测量获得平均折射率，考虑实验测量厚度误差为微米量级，σl为1～10 μm，测量不同的厚度误差下样品折射率的变化值，将数据拟合获得对应的影响曲线，如图8所示。

由图8可知，对于每块样品，随着厚度误差的增大，系统测量样品的折射率偏差也随之增大。对于较厚样品，相同厚度误差对其测量结果影响较小，原因在于当样品较厚时，太赫兹脉冲反射波的光程较大，多次脉冲对主脉冲影响较小。对于厚度为994 μm的样品，当厚度误差为1 μm时，系统测量样品的折射率偏差为10-3左右；当厚度误差为10 μm时，偏差为0.012，符合厚度误差对系统测量不确定度模型。

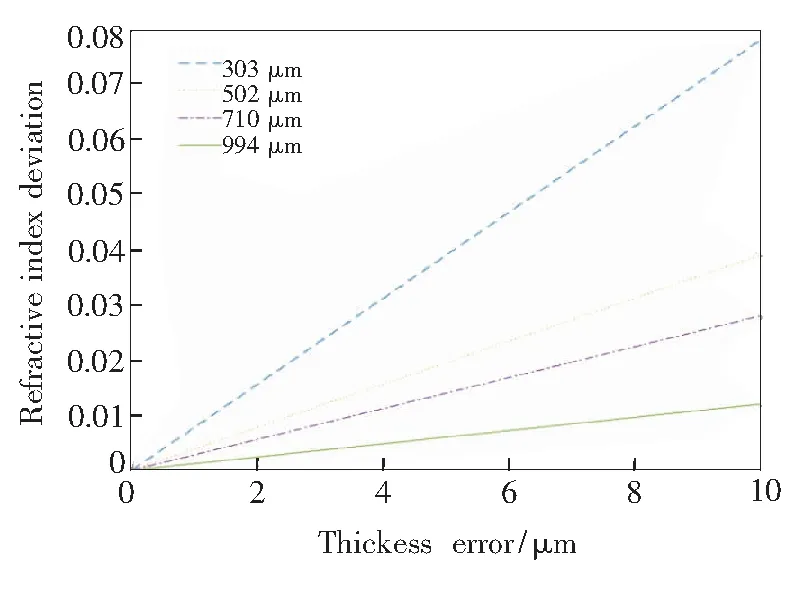
图8 厚度误差对系统提取样品折射率的影响

Fig.8 Effect of sample refractive index carried by thickness error

5 结 论

本文基于菲涅尔公式的透射式THz-TDS光学常数提取方法，分析了厚度误差在测量过程中的不确定度模型，并利用MATLAB编程软件对模型进行了仿真分析。由模型可知，当样品厚度为1 mm时，厚度存在1 μm的误差便会对样品折射率和消光系数的提取产生10-3数量级的误差。以单晶硅片为测试样品进行光谱测量实验，研究厚度误差对系统测量不同厚度的样品折射率的影响情况。实验表明，样品厚度为994 μm(接近1 mm)时，在厚度存在1 μm的测量误差情况下，系统测量的样品折射率偏差为0.001 2，接近模型的仿真值，验证了该分析模型的有效性，对测量过程及结果分析具有一定的指导意义。由于系统各部分在控制精度、响应误差、系统噪声以及实验操作等方面均会对系统测量过程产生影响，故实验结果与模型仿真结果存在一定的差异，有待下一步开展分析验证。