基于增益媒质的亚波长纳米阵列超传输特性研究

孙 龙， 牛凯坤， 冯大政,， 王石语, ， 邢孟道,

(1. 西安电子科技大学 雷达信号处理国家重点实验室， 陕西 西安 710071；2. 西安电子科技大学 信息感知技术协同创新中心， 陕西 西安 710071；3. 中国电子科技集团公司 第三十八研究所， 安徽 合肥 230088；4. 安徽大学 信号与信息处理教育部重点实验室， 安徽 合肥 230039；5． 西安电子科技大学 技术物理学院， 陕西 西安 710071)

1 引 言

伴随纳米科技的蓬勃发展，在针对纳米结构(例如超材料[1-2]、光子晶体[3]和随机介质[4])的研究过程中发现了各种各样新奇的物理现象。受此启发，学者们发明了许多纳米光学器件，如光纤、激光、完美透镜[5]、隐身衣[6-7]和光学非线性器件[8]。近些年，纳米器件因其可观的应用前景引起了广泛的关注。然而，目前大多数的纳米结构都是基于金属的，在光波段下由金属产生的欧姆损耗仍然是横亘在光学器件应用和发展面前的难题。因此，减少甚至完全补偿金属产生的欧姆损耗对纳米技术来说是一个关键的挑战。

目前，针对金属产生的欧姆损耗的问题，研究者们已经提出了一些优化方法。其中，一种方法是对纳米结构的几何形状进行优化设计，其原理是改变纳米结构的电特性并避免在结构中出现角点和拐点等边角形状，但是针对一些复杂的结构，上述方法很难行之有效地解决高损耗的问题。最近，学者们提出了基于染料分子、量子阱和量子点的增益媒质[9-14]作为克服由贵金属引入的欧姆损耗的一种可能的解决方案，在理论和实验方面，增益媒质均展现出良好的放大特性和损耗完全补偿效应。然而，增益媒质需要较强的外部能量来激发以补偿损耗或产生激光，这很大程度上限制了增益媒质在超材料中的应用。另一方面，超常光学传输(EOT)特性近年来也已经引起了广泛的关注[15-16]，其物理本质是一种在电介质和金属的分离界面处行进的电磁表面波：表面等离子体激元(SPP)[17]在金属表面引发的局部场增强作用。当金属膜被放置在周期性阵列中时，将观察到在孔径入口处会产生异常的光学透射和显著的电场增强，上述的电场增强可以协助更多的外部入射光穿透亚波长的孔径，从而产生比经典衍射理论预期要高得多的透射率。因此，将EOT特性引入至含增益媒质的结构中，利用EOT特性和增益媒质之间的耦合机制来减小欧姆损耗被完全补偿时的阈值是一种切实可行的解决办法，上述工作可以显著地扩展增益媒质的应用范围。此外，这项工作对于设计新的增益媒质作用下的纳米等离子体激元实验[18-19]也有着重要的意义。

研究增益媒质产生的放大特性，必须求解麦克斯韦方程和速率方程的耦合，研究者们常用的增益媒质泵浦机理有：高斯泵浦机理、光泵浦机理和均匀泵浦机理。在现有的工作中，为了用上述方程来模拟增益媒质的物理过程，研究者们常用的方法为时域有限差分(FDTD)[20]方法和有限元法(FEM)[21]。为了更精确地计算，本文使用了时域有限差分方法并通过均匀泵浦机理来模拟增益媒质，与频域有限差分(FDFD)[22]方法和有限元法等频域方法相比，时域有限差分方法更有效率，其通过一次计算可以获得宽频带的信息。而针对频域方法，需要计算扫描足够的频率采样点，将会导致计算机存储被大量占用和模拟时间剧增。除此以外，在光泵浦机理中，增益媒质在泵浦频率处吸收能量，并在较低的频率处发射到信号场中。但是，据我们所知，由于泵浦脉冲和探测脉冲在系统中共存，且泵浦脉冲远远大于探测脉冲，它们之间的相互作用将产生误差。另外，探测脉冲必须等待泵浦脉冲完全衰减之后才可以入射，在数值模拟中意味着要消耗大量的时间成本。本文使用均匀泵浦机理来简化泵浦过程，电子可以由均匀泵浦速率fpump从基态能级(N0)泵浦到第三能级(N3)来代替光泵浦的使用从而提高仿真的效率，其中均匀泵浦速率与实验中的光学泵浦强度是成比例的。如果增益媒质的厚度与波长可比拟，则这种简化是有效的[23]。此外，在面对复杂目标、复杂环境等问题时，使用并行技术[24]来突破单个处理器CPU时间的限制可以有效地提高计算效率，极大地缩短计算时间。FDTD方法网格的剖分有着适用于并行计算的天然优势，因此在本研究中使用了并行FDTD加速技术来提高计算仿真的效率。

本文从理论上研究了周期性亚波长孔径阵列中EOT特性与均匀泵浦增益媒质耦合产生的光学放大作用，提出了新颖的含有亚波长周期裂缝阵列的增益/金属/增益模型。在数值模拟过程中，使用了与辅助位微分方程相结合的FDTD方法来对电磁场进行仿真。上述结构可以实现使用更低的泵浦强度激发增益媒质来完全补偿金属区域中本征欧姆损耗的目的。与此同时，随着均匀泵浦速率的增加，整个系统电磁能量的衰减速率被划分为两个不同的阶段，本文对其物理机理进行了讨论。

2 理论及数值计算模型

本文提出的结构如图1所示。增益/金属/增益结构中的金属区域为金属银，其介电常数可以用Drude模型来描述：

(1)

其中ε∞为非谐振介电常数，ωp为等离子体频率，γp为阻尼参数。式(1)中的参数为：ε∞=4.6，ωp=9.0 eV，γp=0.07 eV。

银金属薄膜夹在两层相同的介质板之间，介质的折射率为ng=1.62。当介质被外部入射场泵浦激发时，其中的粒子从基态能级被抽运至高能级，介质将作为增益媒质出现。银金属膜和增益媒质的厚度分别为hm=150 nm和hg=200 nm。此外，将金属薄板作为亚波长周期裂缝阵列，亚波长裂缝的宽度和周期分别设置为l=100 nm和p=520 nm。在FDTD仿真计算中，沿着x方向和y方向使用周期性的边界条件，x方向和y方向的仿真区域大小分别为100 nm和1 040 nm，而沿着z方向采用完全匹配层(PML)进行截断来模拟无限大空间，PML的长度为50 nm，z方向总的仿真区域大小为1 450 nm。入射平面波源为高斯调制的正弦波，其传播方向(k反向)为z方向，极化方向为x方向。仿真过程中的空间步长为Δx=Δy=Δz=5.0×10-9m，时间步长为Δt=8.33×10-18s。

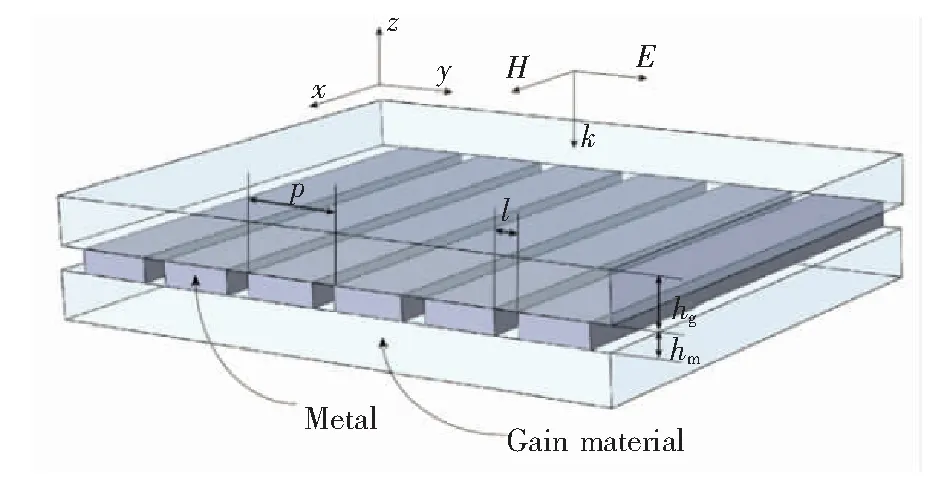
图1 结构示意图

在各向同性介质中，随时间变化的麦克斯韦方程可以表达为：

×E(r,t)=-∂B(r,t)/∂t，

(2)

(3)

其中B(r,t)=μμ0H(r,t)，D(r,t)=εε0E(r,t)+P(r,t)，P(r,t)代表增益媒质的离散电极化强度。电极化强度P将增益引入到麦克斯韦方程中，并且对应于激光上能级N2和激光下能级N1之间的跃迁，除此之外，其时间演化遵循粒子数反转和外部电场相耦合驱动的均匀拓展洛伦兹振荡，因此，它是电磁场和量子物理之间的桥梁。电极化强度P遵循驱动方程[23]：

σaΔN(r,t)E(r,t)，

(4)

其中Γa表示在辐射中心频率ωa处的原子跃迁的线宽，Γa=20 THz，ωa=2π×4.2×1014rad/s，即增益材料的中心波长为714 nm。σa称为P与外部电场的耦合强度，在文中设置为10-4C2/kg。因子ΔN(r,t)=N1(r,t)-N2(r,t)代表第二能级(N2)和第一能级(N1)之间的粒子数翻转，其作用是驱动电极化密度P。其中第一能级(N1)和第二能级(N2)也分别称为激光下能级和激光上能级。

色散洛伦兹增益媒质可以采用图2所示的通用的四能级原子模型进行描述。原子可以通过均匀泵浦速率fpump从第零能级(N0)泵浦到第三能级(N3)，其中，第零能级(N0)和第三能级(N3)也分别被称为基态能级和抽运高能级。在经历了瞬态寿命τ32后，原子可以从抽运高能级(N3)以非辐射的形式转移到亚稳态的激光上能级(N2)。然后，存在于激光上能级(N2)中的原子在瞬态寿命τ21之后，通过受激和自发辐射的方式转移到激光下能级(N1)。最后，经历瞬态寿命τ10后，原子快速地且非辐射地从激光下能级(N1)传输到基态能级(N0)。

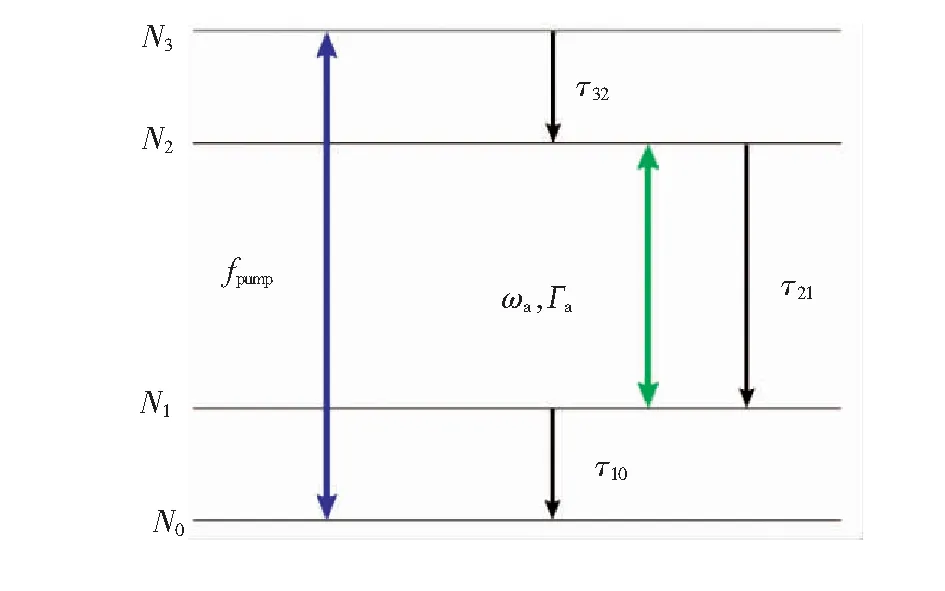
图2 四能级原子系统模型

粒子数满足的速率方程如下：

(5)

(6)

(7)

(8)

其中瞬态寿命τ32、τ21、τ10分别为 5×10-14s、5×10-12s、5×10-14s。粒子总数定义为Ntot=N0+N1+N2+N3=5×1023m-3，其中Ni(i=1,2,3,4) 代表的是每个能级上的粒子数。初始条件为电子仅存在于基能级(N0)，而其他能级均不存在电子，基能级的粒子数(N0)等于Ntot，随后以恒定的泵浦速率fpump将电子从基态能级(N0)泵浦到抽运高能级(N3)。

3 结果与讨论

当增益媒质没有被激发时，它等同于普通的电介质，我们将研究金属的厚度及亚波长裂缝的宽度的改变对超传输特性的影响。首先研究了金属板厚度对传输系数的影响。如图3所示，随着金属板厚度(hm)由100 nm增加到200 nm，3个传输峰均出现了红移现象。其中，在600 nm和950 nm附近整个系统的传输特性得到了增强，而在700 nm左右其传输特性被抑制，总的来说，在光波段内金属板的厚度对超传输特性的影响不是很大。其次，研究了亚波长裂缝的宽度对传输系数的影响。如图4所示，在保持亚波长裂缝的周期p不变的情况下，随着亚波长裂缝的宽度l由50 nm增加到150 nm，在光波段内的两个传输峰出现了蓝移现象且整个系统的传输特性得到了显著增强。由于λ=710 nm接近于激光产生的波长，这符合后续增益媒质的加入、损耗的补偿和激光场的产生，并与实验要求相吻合，对增益媒质的实际应用具有更大的指导意义。因此在随后的研究过程中，将主要对该波长处的谐振峰进行探讨，并采用了第二节中阐述的结构参数。

图3 随金属板厚度变化的传输光谱图

Fig.3 Transmission spectra of passive mediumversusthe thickness of silver slab

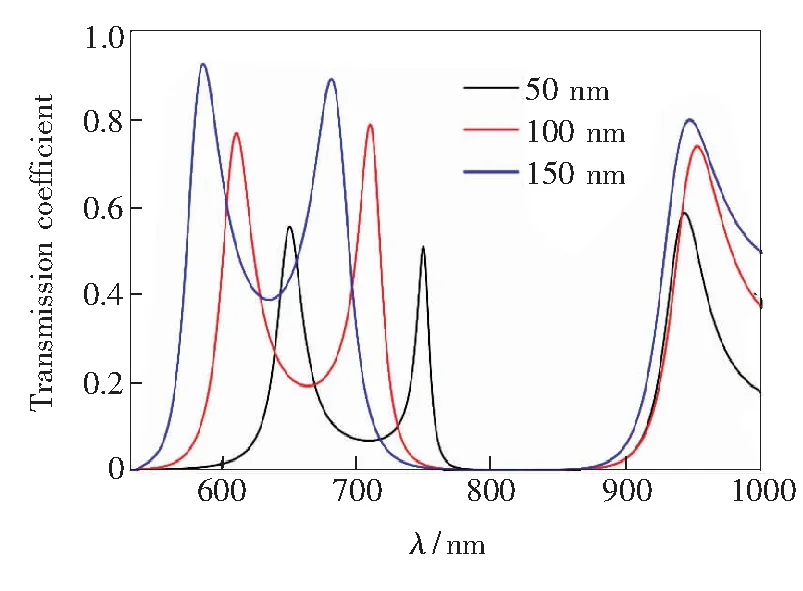
图4 随亚波长裂缝的宽度变化的传输光谱图

Fig.4 Transmission spectra of passive mediumversusthe width of subwavelength aperture

此时hm=150 nm，l=100 nm，整个系统的透射、反射和吸收光谱如图5所示，在λ=616 nm、λ=714 nm和λ=957 nm处分别出现3个谐振峰。值得注意的是，在没有增益加入的情况下，谐振波长下的透射率已经达到78%，这为实现使用较低外部能量完全补偿欧姆损耗的目的提供了有利的先决条件。为了进一步研究谐振峰产生的物理机理，在图6中展示了谐振波长处磁场的场值图。图6(a)、(c)结果表明，此时场强的增强主要集中于裂缝的内部，这种现象表明在λ=616 nm和λ=957 nm处发生共振的原因是裂缝的内部产生了“法布里-珀罗”谐振。而图6(b)中场强的增强主要集中于金属与介质的交界面处，共振产生的物理机理是金属与介质的交界面处产生了表面等离激元，由于亚波长的周期小孔阵列使得更多的电磁场穿透到了金属区域，使得金属和电介质的界面上产生了场聚焦，从而实现了透射效率的提高。

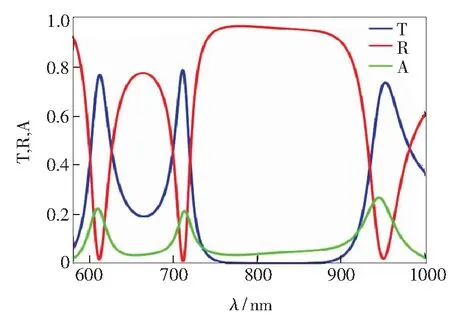
图5 传输、反射和吸收光谱。

Fig.5 Transmission, reflection and absorption spectra of passive medium.

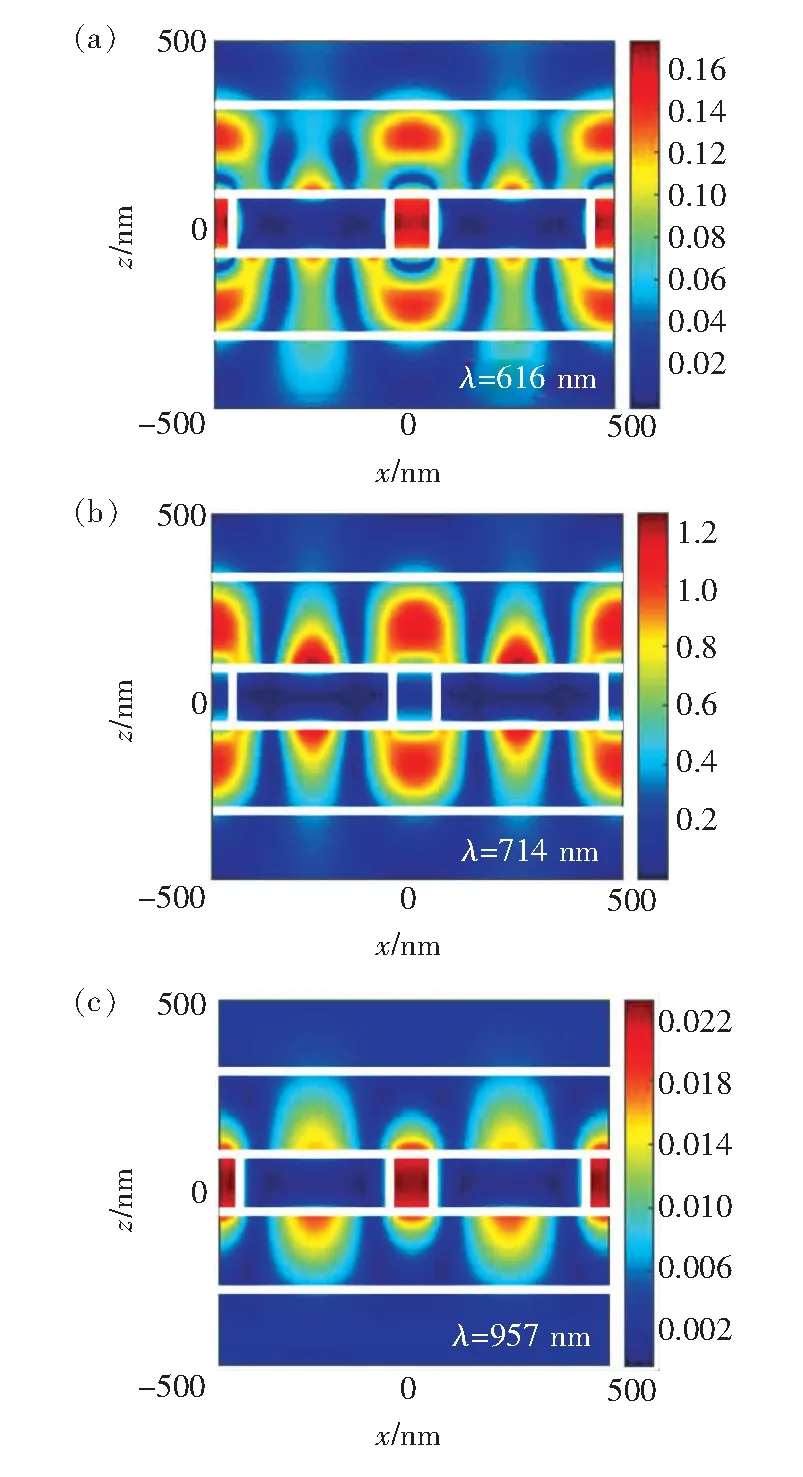
图6 不同波长下磁场场值分布。(a)λ=616 nm；(b)λ=714 nm；(c)λ=957 nm。

Fig.6Hyfield profiles correspond to different wavelengths.(a)λ=616 nm. (b)λ=714 nm. (c)λ=957 nm.

图7(a)～(c)为随均匀泵浦强度变化的传输、反射和吸收光谱与波长的关系图。在均匀泵浦实验中, 控制参数为均匀泵浦强度fpump，随着fpump的值增加，通过增益媒质产生的电磁能量开始补偿由金属产生的本征欧姆损耗，随后使用高斯调制的正弦信号作为探测脉冲来研究整体结构的特性。由图7可以看出，在λ≈714 nm处的吸收光谱不断减小，而此处的传输光谱值不断地增大。值得注意的是，位于λ≈616 nm的谐振峰几乎不受均匀泵浦变化的影响，这是因为其相对应的波长与增益媒质的中心波长相距较远。当fpump达到某一特定值时，泵浦产生足够大的外部能量可以完全补偿存在于结构中的欧姆损耗。在本文中，fpump=1.33×108s-1时达到这种状态。当泵浦强度进一步增加时，λ≈714 nm处的吸收光谱值变为负数，这意味着整个系统此时表现为光放大器，整个系统开始产生增益。对于多数超材料而言，如果需要完全补偿其欧姆损耗，需要较大的泵浦强度。文献[25]中针对含增益媒质渔网结构的研究表明，当均匀泵浦强度为6.6×109s-1时，损耗被完全补偿。文献[23]中针对含增益媒质开口谐振环结构的研究表明，当均匀泵浦强度为1.9×109s-1时，损耗被完全补偿。而针对本文提出的结构，均匀泵浦强度仅为1.33×108s-1时，损耗即被增益媒质完全补偿。此外，图8为引入增益媒质(fpump=1.33×108s-1)后，谐振波长λ≈714 nm处磁场的场值图，与图6(b)对比可知，在引入增益媒质之后，其与整个系统的耦合放大了表面等离激元的作用，使得金属与介质的交界面处的场强进一步增大，从而达到补偿金属损耗的效果。从本文数值结果可以看出，由于SPP和增益媒质之间的耦合，使用显著减小的泵浦强度就能够实现对欧姆损耗的完全补偿。

图7 不同泵浦速率下整个结构的传输(a)、反射(b)、吸收(c)光谱。

Fig.7 Transmission(a), reflection(b) and absorption(c) spectra of the structure with different pumping ratefpump.

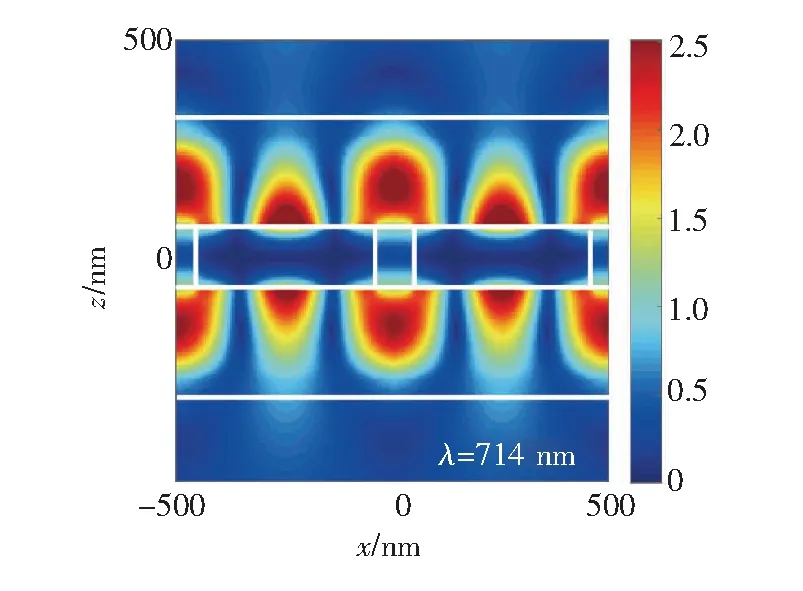
图8 引入增益媒质(fpump=1.33×108s-1)后，λ=714 nm处的磁场场值分布。

Fig.8Hyfield profiles correspond toλ=714 nm andfpump=1.33×108s-1.

另一方面，当欧姆损耗被增益媒质完全补偿时，位于中心频率λ≈714 nm的位置可以实现100%的透射。这种情况类似于EOT现象中所观察到的完全透射特性，即当金属满足Im(εm)=0时，其欧姆损耗亦趋于0，该状态下的金属被称为完美金属。为了深入研究上述的完全透射特性，将无增益(fpump=0)并且金属介电常数的虚部被人为地设置为零所构成的完美金属(虚线)与当增益媒质(fpump=1.33×108s-1)完全补偿了金属中的欧姆损耗时(实线)的透射和反射系数进行了对比，如图9所示。研究表明，上述两种情况的结果具有完美的一致性，这说明当增益媒质提供的能量高到足以完全补偿欧姆损耗时，有增益的结构中的金属银可以被无增益时的完美金属所替代。

图9 当泵浦速率为1.33×108s-1时，整个透射(蓝色虚线)和反射(红色虚线)光谱以及将结构中的金属区域替换为完美金属并且泵浦速率为零时透射(蓝色实线)和反射(红色实线)光谱。

Fig.9 Transmission (blue dashed line) and reflection (red dashed line) spectra simulated withfpump=1.33×108s-1. Blue solid line and red solid line show the results of computations in which the metallic regions of the structure are assumed to behave as perfect metals.

最后，为了研究系统的整体响应，本文将存储在整个系统中电磁能量的总衰减速率划分为不同的阶段进行分析。系统的总衰减速率(ΓT)可以被定义为fpump的函数：

ΓT(fpump)=Γrad+ΓOhm-Γg(fpump),

(9)

其中Γrad表示本征辐射损耗的衰减速率，ΓOhm是欧姆损耗的衰减速率。 值得注意的是，ΓOhm仅与贵金属的材料特性有关，Γrad的值仅与结构的几何形状有关，它们均与fpump的值无关。另一方面，Γg(fpump)是关于通过增益媒质泵浦进入系统中的外部能量的函数，当没有增益媒质泵浦外部能量时，显然满足Γg(fpump=0)=0。

得出定值Γrad和ΓOhm的结果后，Γg随泵浦速率变化的规律可以通过观察随着泵浦速率的增加，该结构中的传输谐振峰线宽的变化来获得。如图10所示，衰减速率均由无外部泵浦时整个系统的总衰减速率(ΓT(fpump=0)=Γrad+ΓOhm)进行归一化处理。 图10中的水平红线表示的是归一化欧姆损耗的值ΓOhm/Γ(fpump=0)，蓝色点线表示的是Γg/ΓT(fpump=0)随fpump的变化而得到的结果；插图表示的是归一化的总衰减率ΓT/ΓT(fpump=0)随泵浦速率变化的结果。

从图10可以看出，该系统可以分解为两个不同的阶段(表示为A和B)。从物理角度看，当泵浦强度fpump<1.33×108s-1(图10中的区域A)时，仿真结果表明，当泵浦速率较低时，通过增益媒质产生的电磁能量首先被用来补偿欧姆损耗。此时增益媒质表现为光放大器，它可以有效地减小所考虑系统传输谐振的总线宽。当fpump=1.33×108s-1时，归一化欧姆损耗(ΓOhm/Γ(fpump=0))和外部能量Γg(fpump=1.33×108s-1)的值相等，该结果也恰好验证了图7中的结果，即当fpump=1.33×108s-1时，增益媒质可以完全补偿系统中的欧姆损耗。一旦欧姆损耗被完全补偿，并进一步增加fpump的值后，整个系统将会进入一个新的状态，即图10中的区域B，此时增益媒质提供的能量开始补偿辐射损耗。

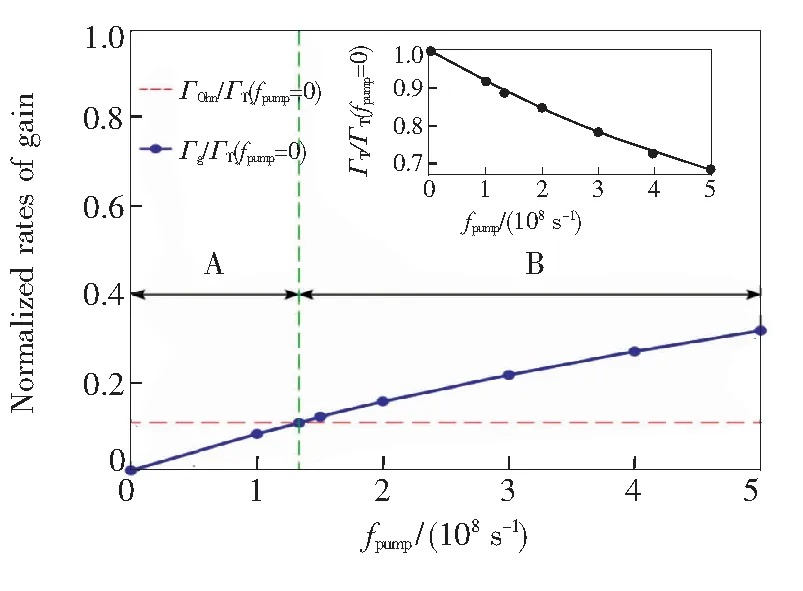
图10 归一化的增益率Γg/Γ(fpump=0) (蓝线)。插图为归一化的总衰减率ΓT/ΓT(fpump=0)。

Fig.10 Normalized rate of gainΓg/Γ(fpump=0) (blue line) as a function offpump. The inset renders the normalized total decay rateΓT/ΓT(fpump=0)versusthe pumping rate.

4 结 论

本文从理论上研究了EOT现象与通过均匀泵浦激发的增益媒质耦合机制中的损耗补偿特性。具体而言，本文分析了增益/金属/增益结构的光谱响应，该结构为掺杂增益媒质的两层薄介质层之间夹着一层亚波长周期性裂缝阵列金属薄膜。模拟结果表明，在上述结构中，由于亚波长的周期裂缝阵列使得金属与介质的交界面处产生了表面等离激元，使增益媒质在抑制损耗时变得更加简单有效，从而实现了使用更低的泵浦强度激发增益媒质完全补偿金属区域中的本征欧姆损耗的目的。上述研究结果对增益媒质、超材料等新颖材料的实验设计有着十分重要的指导意义。