基于卷积神经网络的图像去雾算法

2019-03-26陈清江柴昱洲

液晶与显示 2019年2期

陈清江, 张雪*, 柴昱洲

(1.西安建筑科技大学理学院, 陕西西安 710055; 2.空间电子信息技术研究院，陕西西安 710000)

1 引言

由于大气的散射作用，在雾天采集的图像通常细节模糊，色彩偏移，对比度较低，能见度较低，给交通系统、户外视觉系统以及人们的生活带来了严重的影响。因此，图像去雾的研究在计算机视觉以及计算机图像领域有着重要的现实意义。近年来，单幅图像去雾技术取得了重大突破，这些方法的成功得益于强有力的先验知识与假设。目前对于有雾图像去雾的算法主要有3类:基于非模型的图像去雾算法，基于模型的图像去雾算法和基于学习的去雾算法。基于非模型的图像去雾算法是从人类视觉感受出发，直接增强图像对比度，修正图像色彩对比度以改善图像质量。Fan等[1]提出了一种基于Retinex的图像去雾算法。Kim等[2]提出了一种用于对比度增强的直方图均衡化算法。基于模型的图像复原算法从图像退化的物理模型出发,恢复出尽可能逼真的清晰图像。Tan等[3]使用马尔可夫随机场(MRF)模型拉伸图像对比度，然而，输出的去雾图像颜色通常趋于最大饱和度，所以复原结果在场景深度突变处易产生光晕效应。Fattal等[4]提出了基于独立分量分析的方法(ICA)，使用MRF模型推断整幅图像的颜色，由于该方法基于局部小方块的统计独立假设，处理浓雾图像复杂度高。He等[5]提出了一种基于暗原色先验知识统计的方法，该方法具备物理有效性，但是当场景目标在很大的区域时，暗原色先验知识统计可能无效，并且修补的传输图层次不够明显，不能有效区分距离的远近。Meng等[6]提出了一种有效的正则化方法，从对传输函数固有边界约束的探索中恢复出了无雾图像。Li等[7]提出了一种联合估计场景深度和从有雾视频序列中恢复清晰图像的方法。Zhu 等[8]在对场景深度建模之前提出了颜色衰减，利用恢复的深度信息，对给定的有雾图像进行去雾处理。尽管上述算法取得了很大的进步，但它们仍然依赖于各种先验知识，并且仍然有局限性。目前，随着深度学习理论的不断发展，将该理论用于图像去雾领域获得了较好的效果，因此，基于学习的去雾算法可以被认为是第3类去雾算法。Ren等[9]利用卷积神经网络估计了场景的透射率，根据大气散射模型，恢复出无雾图像。

本文提出了一种不需要基于先验知识和假设的去雾算法，避免了对大气光值和传输图的估计。网络设计分为两个部分：第一部分进行特征提取，在多尺度映射的基础上，使用反卷积增加图像的空间维度；第二部分则是浅层与深层的合并，避免了图像信息的丢失。

2 雾天图像退化的物理模型

用大气散射模型描述雾天图像[10-12]的形成，大气散射模型首先由McCartney[13]提出，由Narasimhan和Nayar[14]进一步发展。大气散射模型为：

L(x)=t(x)H(x)+a(1-t(x))，

(1)

式中：x为像素点的空间坐标；L(x)为输入图像(即观察到的有雾图像)像素值；H(x)为输出图像(即恢复的无雾图像)像素值；a为全局常量，表示全球大气光值；t(x)为透射率图，即传输图。式中右边第一项为直接衰减项，描述了场景辐射率在介质中衰减的结果；第二项为大气光照，大气光照反应了全局大气光的散射导致场景颜色的偏移。传输图t(x)描述的是光线通过大气媒介传播到达成像设备的过程中没有被散射的部分，它能反映图像上目标场景的远近层次。当大气同质时，传输图t(x)可以定义为：

t(x)=e-βd(x)，

(2)

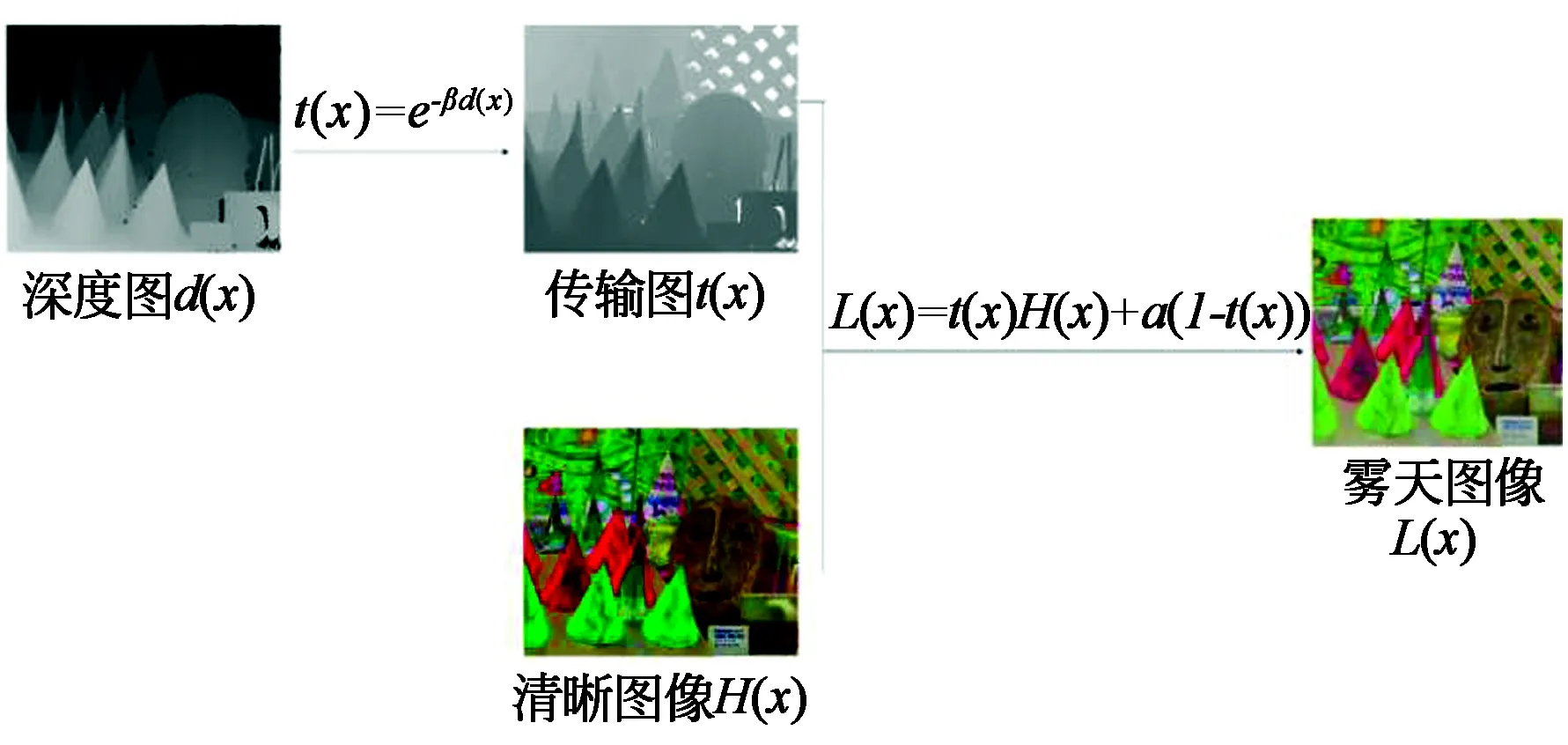
图1 雾天图像形成Fig.1 Fog image formation

式中：β为散射率，当大气均匀时，在一定时刻对于整幅图像来说β是一个定值，d(x)为场景对象到传感器的距离，即场景深度。

因此，去雾的目的是从有雾图像L(x)中估算出大气光值a和传输图t(x)，从而恢复出无雾图像H(x)，因此，这是一个病态问题。雾天图像的形成过程如图1所示。

3 多尺度卷积神经网络的去雾方法

卷积神经网络是一种前馈型人工神经网络，提供了一种端到端的学习模型，本文提出了一种多尺度卷积神经网络，即通过不同尺度的滤波器进行卷积运算自动学习输入图像的特征，并通过反向误差传播不断修正特征参数。卷积神经网络相较于传统的图像处理算法的优点之一在于，避免了对图像复杂的前期预处理过程如人工提取特征等，可以直接输入原始图像。

3.1 本文算法去雾网络结构

本文网络结构是一个端到端的系统,它直接学习和估计雾天图像与其无雾清晰图像之间的映射关系，输入雾天图像，输出估计的无雾清晰图像。网络结构主要分为特征提取层，多尺度映射层，反卷积重建层以及浅层特征与深层特征合并层。网络结构如图2所示。

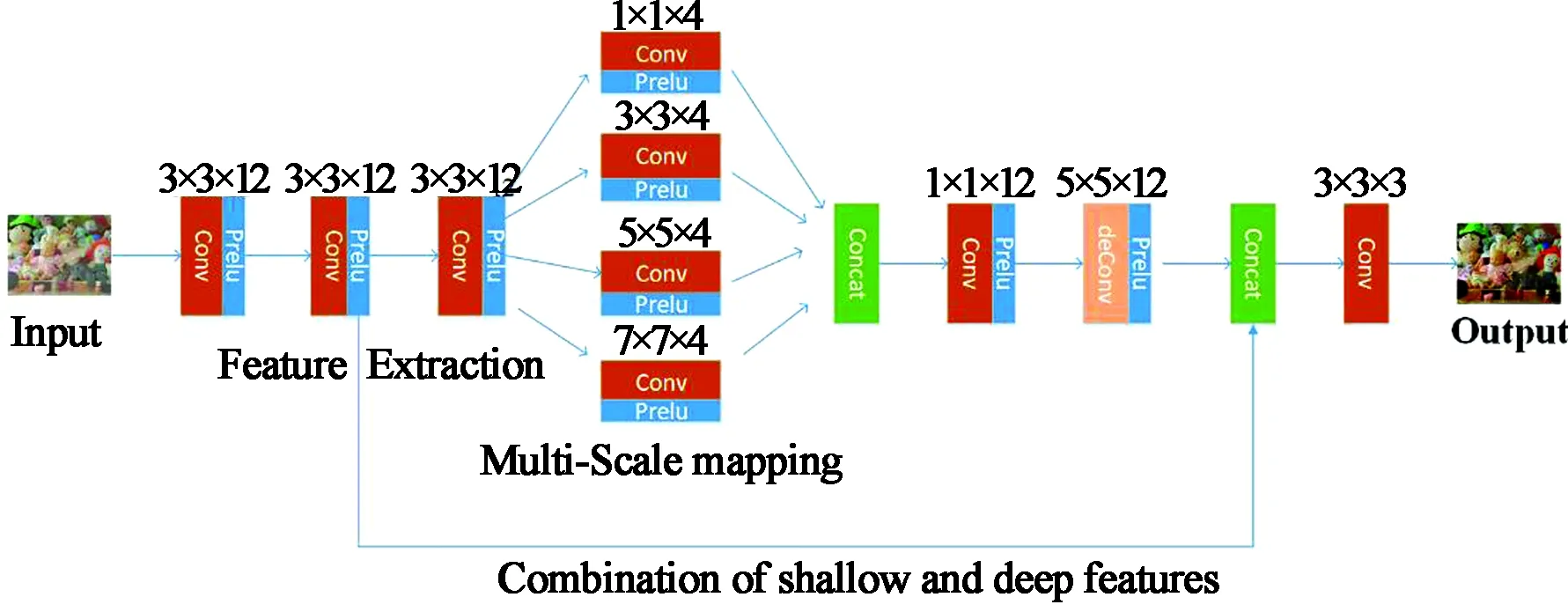
图2 本文网络结构Fig.2 Network structure of this paper

3.1.1 特征提取

特征提取层包括3个卷积层，直接从原始雾天图像中提取特征，设置每层滤波器尺寸都为3×3，个数都为12，逐步提取雾天图像的细节信息。卷积操作进行特征提取的计算公式为

Gi(Y)=Wi*Gi-1(Y)，

(3)

式中，Gi(Y)为输出的第i层的特征图，Wi为第i层的卷积核，Gi-1(Y)为i-1层的特征图。*表示卷积操作。

本文选用参数修正线性单元(PReLU)作为网络结构的激活函数,除了最后一层，其余每个卷积层与反卷积层的末端都接入此激活函数。Relu梯度在大多数情况下是一个常数，因此,在一定程度上避免了梯度消失问题，参数修正线性单元(PReLU)不仅具有以上优点，而且还可以加快网络的收敛速度。因此，PReLU比Relu更加有效。PReLU公式为

KPReLU(xi)=max(xi,0)+aimin(0,xi)，

(4)

式中:xi为第i层的正区间输入信号，ai为第i层的负区间的权系数。PReLU克服了ReLU的“特征死亡”缺点。所以卷积层的最终输出为

Gi(Y)=KPReLU(Wi*Gi-1(Y)+Bi)，

(5)

式中:Gi(Y)为最终输出的第i层的特征图，Bi为第i层的偏置值。

3.1.2 多尺度映射

在网络结构的第四层采用多尺度映射，提取多尺度规模结构信息。通过4种尺寸分别为1×1,3×3,5×5,7×7的滤波器进行特征提取，滤波器是平行的，它们每一个都输出4个特征图，然后连接成16个特征图，由于雾天图像恢复通常依赖于短尺度和长尺度的纹理信息，因此使用不同尺度的滤波器提取特征。然后将16个特征图输入第五层，采用12个1×1的滤波器进行卷积,达到维度收缩，降低计算复杂度。详细参数记录如表1所示。(其中，Conv4-1表示第四层的滤波器大小为1×1的卷积层)

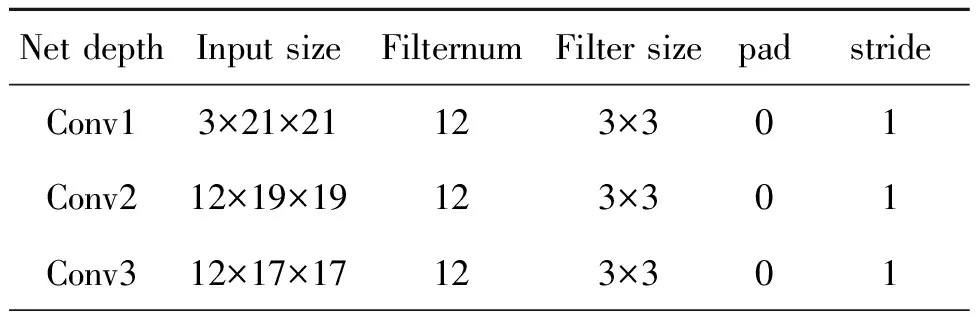
表1 网络模型参数Tab.1 Network model parameters

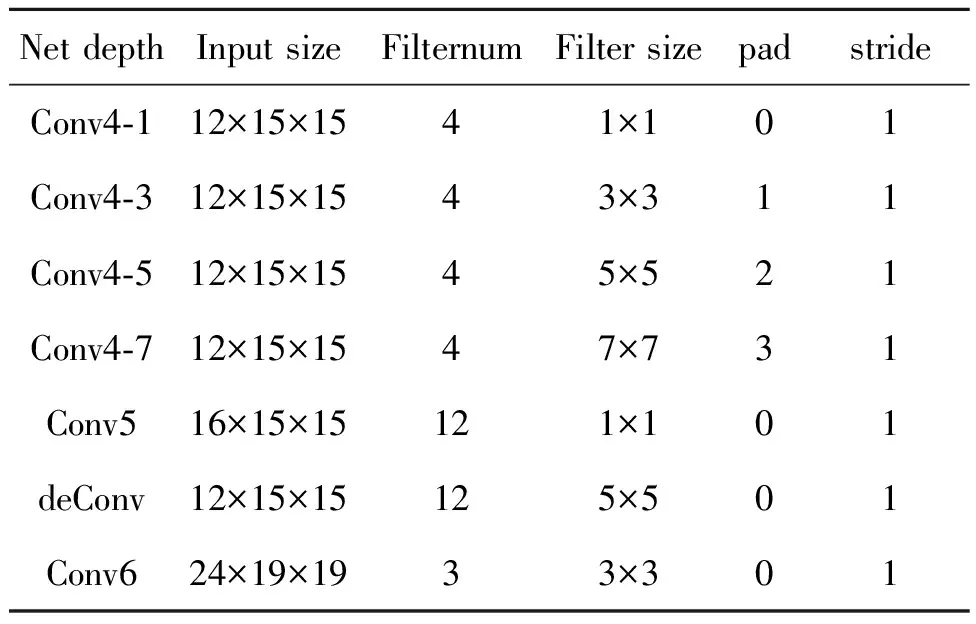
续表

3.1.3 反卷积

反卷积层(Deconvolution)在本网络结构中起着一个重要作用，目的是增加图像的空间维度，实现重建过程, 该层相当于上采样。当步长s和滤波器尺寸k相等时，卷积将输入图像缩小k倍，而反卷积则会将输入图像放大k倍。因此，本文采用反卷积来扩展图像空间尺寸，将进行浅层特征与深层特征的合并。如果将反卷积换为卷积，则会降低网络的非线性性。使用滤波器尺寸分别为3×3，5×5，7×7的反卷积核大小进行反卷积，得到当滤波器尺寸为5×5去雾质量最好，所以本文采用尺寸为5×5×12的滤波器来聚合先前的特征向量，该过程可以表示为

Gi(Y)=σ[Wi*Gi-1(Y)+B]，

(6)

式中：Gi(Y)为第i层反卷积层的输出，Wi为反卷积层的权重参数，Gi-1(Y)为第i-1层卷积层的输出特征图。因此，该层输出图像块的大小可以表示为

o=s(I-1)+R-2p，

(7)

式中：I为输入的反卷积层图像的大小，R为反卷积核的大小，s为步长，p为零填充大小。

3.1.4 浅层与深层特征合并

浅层网络恢复出的图像较为粗糙，缺少高频细节，相反,深度网络可以更精确地恢复高频细节，因此，将反卷积层与第二层卷积层的特征图进行合并，共有24个特征图，如此进行连接，将删除特征图中的伪像素，减少细节信息的损失。最后，输入3×3×3的卷积层，输出清晰无雾图像。整个网络结构实现了精细的去雾效果。

3.2 损失函数

在网络训练过程中，使用EuclideanLoss作为损失函数，用来计算输入雾天图像与预测的无雾图像两者差值的平方和，公式为

(8)

其中：yi表示第i组清晰图像值，xi表示网络结构的第i组输出值，N为样本训练数目。对于网络结构的训练，需要收集大量的标签数据，而现实中的大量的雾天图像和对应的清晰图像是不可用的，因此，我们使用通过大气散射模型得到的雾天图像来训练网络。利用随机梯度下降法(SGD)和反向传播算法进行网络优化得到最优的网络参数。

4 实验与结果分析

本节描述了实验步骤与设置，实验数据的获取，并且将本文算法的去雾结果与其它算法的去雾结果进行主观与客观的对比分析。采用结构相似度(SSIM)[15]和峰值信噪比(PSNR)[16]两个重要的图像评价标准对合成雾天图像去雾结果进行对比。

4.1 实验步骤与设置

本文实验步骤为：

(1)获取雾天图像数据集；

(2)进行网络模型的训练与测试；

(3)基于合成雾天图像数据集的去雾结果与分析；

(4)基于真实雾天图像数据集的去雾结果与分析。

本文实验设置为：利用Caffe框架实现网络，每层的权重均采用均值为0，方差为0.001的高斯分布进行随机初始化。网络模型采用固定的学习率，设置为0.000 01，动量参数设置为0.9，迭代次数为105次，本文提出的网络结构其训练速度快，去雾效果优越。

4.2 实验数据

本文实验数据分为两类，第一类来源于自然场景下的雾天图像，第二类来源于Middlebury Stereo Datasets，选出58幅清晰图像以及所对应的深度图，将这58幅图像通过大气散射模型式(1)与式(2)建立雾天图像数据集。散射率β随机设置为(0.75,1.5),因为如果散射率β太小，形成的雾图存在噪声，太大会使得传输图变成0。大气光值a随机设置为(0.7,1.0)。每组图像随机选取两个散射率β值和两个大气光值a，得到232幅雾天图像，将200幅雾天图像作为训练样本，32幅作为测试样本。为扩大数据的样本与提高训练数据的有效性，将训练样本与测试样本的每组图像首先分别进行90°，180°，270°的旋转，然后进行2,3,4,5倍的放大，分别得到4 000幅和640幅雾天图像作为最终的训练样本与测试样本。图3所示为形成的部分雾天图像。

图3 部分雾天图像Fig.3 Part of the fog image

4.3 基于合成雾天图像数据集的去雾结果与分析

为验证本文算法对合成雾天图像的去雾效果，将本文算法与He 算法[5]、Meng 算法[6], Li 算法[7]、Zhu 算法[8]、Ren 算法[9]进行了比较。合成雾天图像通过大气散射模型进行合成。在图4～图6中，展示了部分合成雾天图像的去雾结果对比。

图4 不同算法对雾天图像Cones的去雾结果Fig.4 Defogging results of fog image cones with different algorithms

图5 不同算法对雾天图像Dolls的去雾结果Fig.5 Defogging results of fog image dolls with different algorithms

图6 不同算法对雾天图像teddy的去雾结果Fig.6 Defogging results of fog image teddy with different algorithms

由图4～图6可看出，He 算法[5]和Meng 算法[6]产生了过度强化和过度饱和的结果。例如，He 算法在图dools和teddy上产生了伪影现象，Meng 算法在图dools中整体背景颜色偏白。Li 算法[7]、Zhu 算法[8]和Ren 算法[9]方法仍然可以在几个区域去雾，并且去雾图像较为清晰。本文的去雾图像更加平滑，可以去除输入雾天图像中的薄雾，细节和纹理更加明显，可以恢复颜色和外观，而且接近真实清晰图像。

为了定量地评价这些方法，我们选取Middlebury Stereo Datasets的合成有雾图像作为测试集，使用结构相似度(SSIM)[15]和峰值信噪比(PSNR)[16]两个重要的图像评价标准来衡量每一对无雾图像和去雾结果之间的差异。

首先，KPSNR是评价图像质量最广泛使用的客观标准之一。它是一种全参考评价方法，需要参考图像。给定两个图像，它们之间的PSNR定义为:

(9)

式中:fin为清晰无雾图像，fout为去雾图像。如果PSNR值越大，图像的失真就越小。这意味着图像质量越高，去雾性能越好。

KSSIM被认为与人类视觉系统的质量感知有关,它衡量图像亮度、对比度和结构的相似性。KSSIM的定义如下:

(10)

合成雾天图像不同算法的客观指标对比结果如表2所示，本文算法的PSNR值和SSIM值相对其他经典算法都比较高，和Ren 等[9]利用卷积神经网络所恢复的去雾图像相比，无论是PSNR值还是SSIM值，都有较大提高。因此，说明本文的网络模型具有明显的优势且有良好的去雾能力。

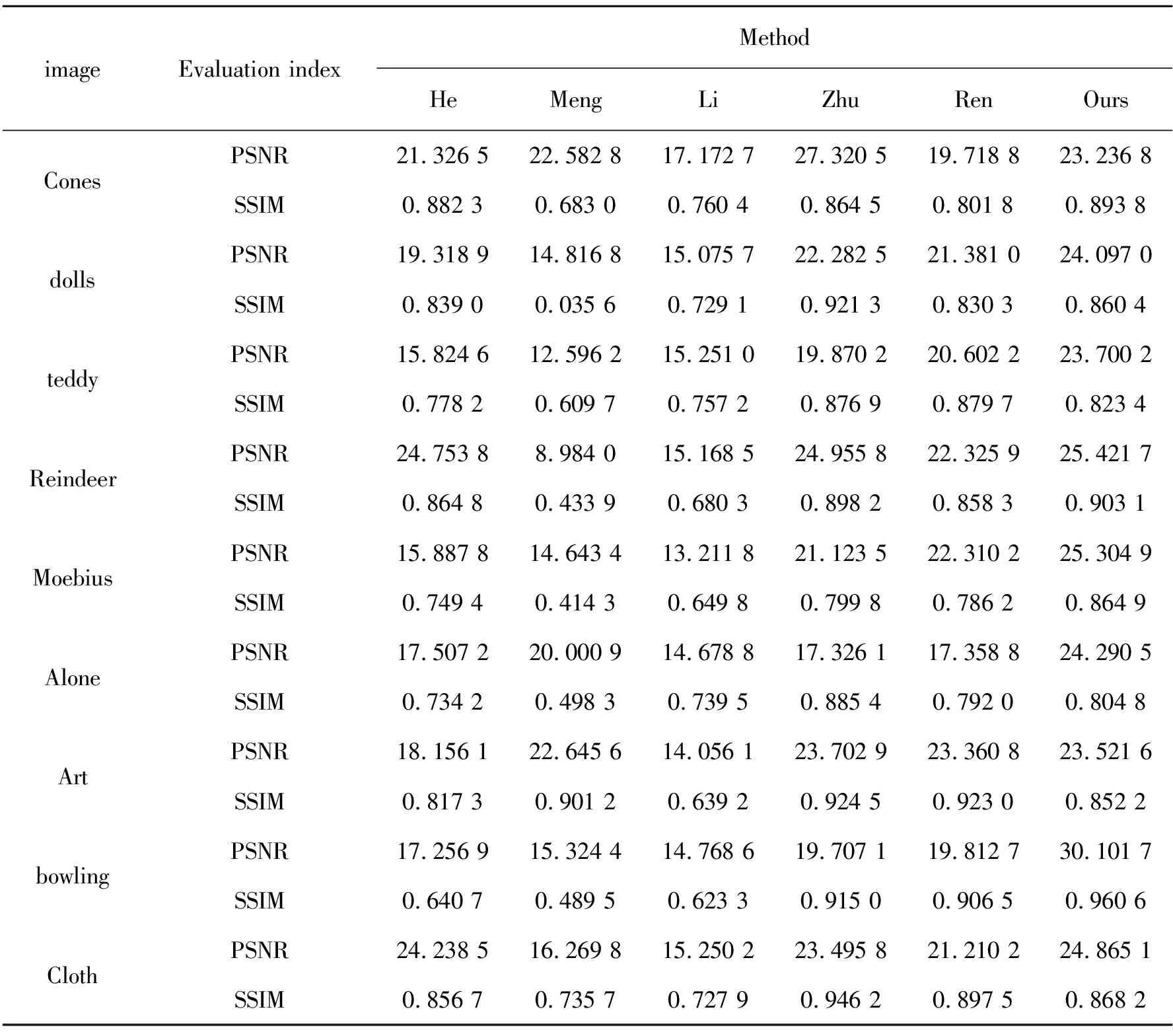
表2 不同算法的PSNR与SSIM的对比结果Tab.2 Comparison results of PSNR and SSIM with different algorithms

4.4 基于真实雾天图像数据集的去雾结果与分析

本文讨论了有雾图像的一些去雾算法，以验证本文所提供算法的有效性。首选现实世界中经常使用的雾天图像，将所提出的方法与He 算法[5]、Meng算法[6]、Li 算法[7]、Zhu算法[8]、Ren 算法[9]进行比较，如图7与图8所示。在图像恢复中，信息熵(Entropy)表示图像的信息量；平均梯度(Average gradient)表示图像层次的丰富程度，指标越大，图像细节信息越明显，获取图像信息越丰富，图9与图10展示了不同算法在真实雾天图像上的去雾评价指标的结果。

图7 自然雾天图像pumpkin的去雾结果对比Fig.7 Comparison of defogging results of natural foggy images of pumpkin

图8 自然雾天图像girls的去雾结果对比Fig.8 Comparison of defogging results of natural foggy images of house girls

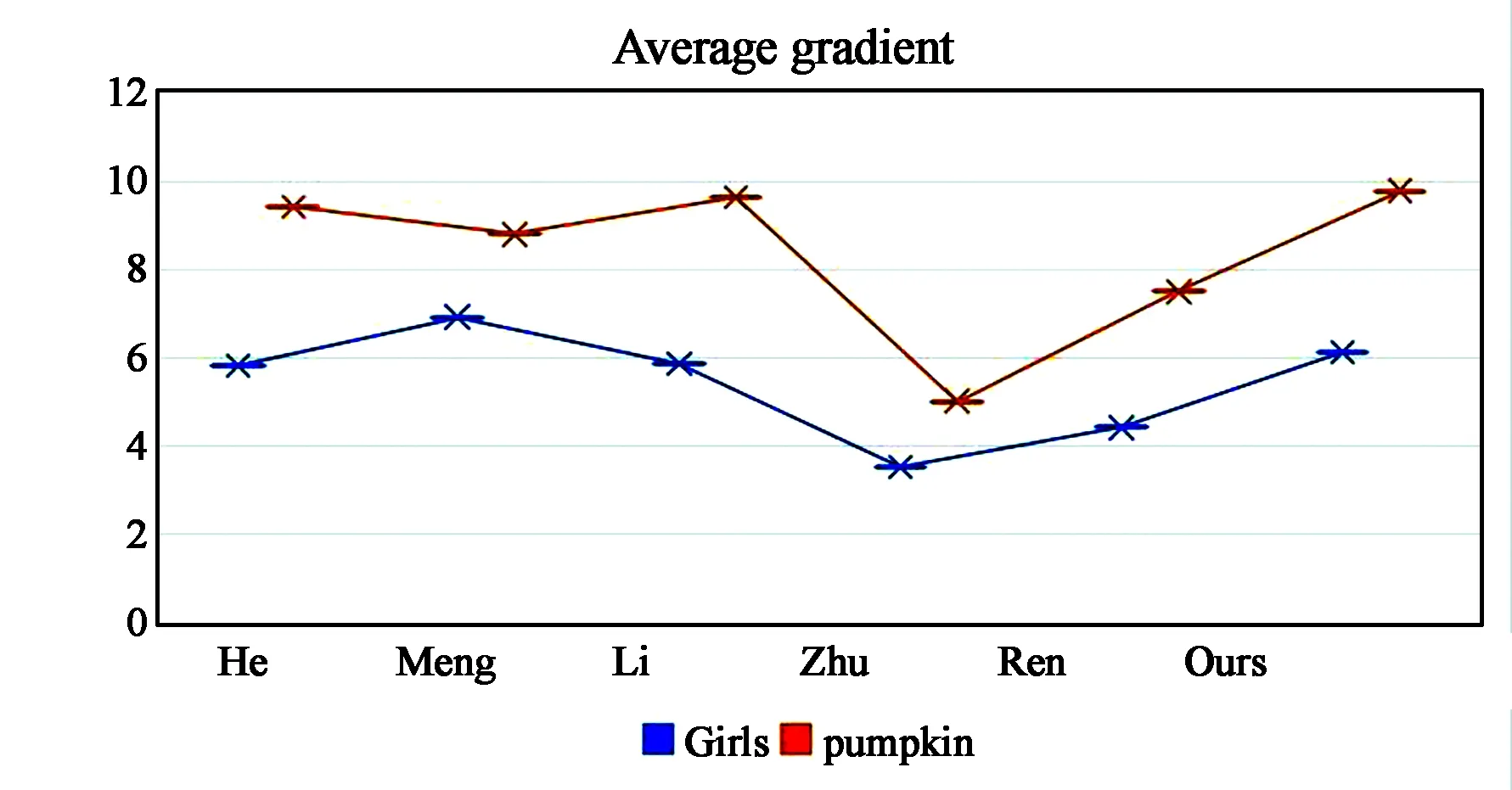
图9 不同算法的平均梯度的对比结果Fig.9 Comparison results of the average gradient with different algorithms

图10 不同算法的信息熵的对比结果Fig.10 Comparison results of information entropy with different algorithms

由图7～图8可看出，He 算法[5]、Meng 算法[6]与Li 算法[7]高估了雾霾的厚度，对天空区域敏感，因此出现过度增强的区域，恢复的图像颜色存在失真情况，如He 算法对于自然雾天图像Pumpkin的去雾，天空区域颜色较深，变成了深蓝色，在图像girls中面部颜色也有所加深，Li 算法在图pumpkin中，天空区域变成了绿色，Meng 算法在图像Girls中，面部和头发处颜色偏白；Zhu 算法[8]与Ren 算法[9]的结果在天空区域都有显著改善，可以增加图像细节，提高图像的可见性；然而，在稠密的雾霾区域仍有一些残留的雾霾。因为卷积神经网络能够学习天空区域来保持颜色，并保证在其他区域有良好的去雾效果，其中块属性可以在网络结构的隐藏层中学习，它有助于在天空中达到良好的去雾效果。因此，本文方法在具有挑战性的天空区域产生了良好的除雾性能，在没有颜色扭曲或伪影的稠密雾霾区域更加直观，结果具有良好的对比度、生动的色彩和视觉效果，并且由图9～图10可看出评价指标值都相对较高，表明本文去雾算法的效果较为优越。