一种解决遮挡问题的跟踪方法

吴水琴, 毛 耀, 刘 琼, 李志俊

(1. 中国科学院 光束控制重点实验室，四川 成都 610209;2. 中国科学院 光电技术研究所，四川 成都 610209;3. 中国科学院大学，北京101400)

1 引 言

目标跟踪是指对一段连续视频和图像序列中的目标进行状态估计和跟踪的过程，是计算机视觉的主要研究方向之一，现已被广泛应用于视频监控领域、军事领域和人机交互的游戏领域。随着嵌入式硬件的发展和图像序列集的完善，目前已涌现了大量的跟踪算法。但遮挡问题一直跟踪研究中的难点，由于目标被局部或全局遮挡时，目标特征信息的减少导致跟踪算法失效或提取到假目标。目前研究人员已经提出一些方法来解决跟踪中的遮挡问题：TLD跟踪算法[1]通过在跟踪算法中加入遮挡检测机制和检测模块来解决遮挡问题，其根据前向后向误差法判断目标是否跟踪失败，若检测出跟踪失败则启用检测模块重新检测出目标。但TLD跟踪算法的帧频低，往往达不到实时性要求。分块匹配算法[2]将目标分为多个子区域，利用各个子区域的特征进行跟踪。其充分利用了目标未被遮挡的区域进行跟踪，避免了被遮挡部分带来的不利影响，能够有效的解决局部遮挡跟踪问题。但是分块匹配算法无法解决目标被全部遮挡的跟踪问题；且分块匹配算法的跟踪性能受子块大小的影响，若子块过大时跟踪算法的抗遮挡能力下降，子块过小时跟踪算法的跟踪性能下降。研究人员利用Mean Shift跟踪算法与Kalman预测融合的方法[3]进行跟踪，使用Bhattacharyya系数法进行遮挡判定，若判定目标处于正常跟踪状态时，使用Mean Shift算法进行跟踪；若判定目标处于遮挡状态时，则使用Kalman预测滤波器进行预测跟踪。由于Kalman预测滤波器受给定测量信息和遮挡判定的影响，若Mean Shift算法发生漂移导致Kalman预测滤波器中的历史数据信息存在错误，会影响遮挡状态下Kalman预测滤波器的预测性能；若遮挡判定不准确，当目标进入遮挡物时没有检测出遮挡状态或检测出遮挡状态时跟踪算法已经失效，Kalman预测滤波器未启动或未及时启动，会导致跟踪失效[4-6]。针对上述问题，本文提出一种基于直方图比的背景加权的Mean Shift算法与Kalman预测滤波器融合的方法，与Mean Shift算法相比，其具有如下优势：

(1)本文算法通过改进目标的表观模型来提高目标在正常跟踪状态的跟踪精度，从而提高Kalman预测性能。

(2)本文算法通过减少背景像素的影响来优化Bhattacharyya系数值，增大正常跟踪状态下和遮挡状态下Bhattacharyya系数的差值，提高遮挡检测的敏感性。

本文使用图片序列验证算法的有效性，通过实验表明，本文算法能够提高遮挡时的跟踪性能。

2 跟踪算法原理

2.1 Mean Shift算法原理

Mean Shift算法是利用图像的颜色直方图信息作为搜索匹配的特征，利用Bhattacharyya系数作为目标模板和候选模板的相似度函数，完成特征的匹配。在跟踪过程中，通常使用矩形框手动选择目标区域，目标区域中有m个像素点，特征空间中特征值的个数为n，对目标区域的特征值u进行建模：

(1)

(2)

候选区域的模型与式(1)类似，第N帧中特征值u的概率模型为：

(3)

Ch为归一化常数，与(1)中的C对应。

使用Bhattacharyya系数来度量目标模板和候选模板的相似度，其定义为：

(4)

其中，ρ(y)的值在[0,1]之间，ρ(y)的值越大，表示2个模板的相似度越高。通过对相似度函数求最大值，得到目标的位置为：

(5)

式中：

g(x)=-k′(x)，

(6)

(7)

其中:y0表示目标当前的位置，y1为迭代后的新位置。

2.2 基于直方图比的背景加权的Mean Shift算法

由于经典的Mean Shift算法中目标初始模板受背景像素的影响[8-10]，所以本文使用基于直方图比的背景加权的Mean Shift算法(HRBW Mean Shift)，通过在目标模板外的环形区域内建立背景直方图，使用基于目标直方图和背景直方图的对数似然比值推导出的权值作为背景加权因子，通过在目标模板中加入背景加权因子来减少背景像素的影响，从而提高算法的跟踪能力和遮挡检测能力。

(1)背景直方图建模

如图1所示，红色矩形框为目标区域，目标外部环形区域为背景区域，背景区域的模型为式(8)：

(8)

(2)计算特征值为u的对数似然比值

(9)

式中，η是为了防止qu或bu为0的错误情况，所以给η赋值为一个很小的值(0.1×10-6)。上式中通过非线性变换，使得和背景颜色特征相同的特征值在目标直方图中所占的权重较小。

图1 背景直方图建模图Fig.1 Picture of background histogram modeling

(3)计算变换后的背景加权系数

根据式(9)得出的对数似然比值，使得和背景颜色特征相同的特征值在目标直方图中所占的权重较小，使得属于目标直方图的特征的权重较大。得到背景加权系数μu为：

(10)

其中：Lmax是Lu中的最大值，Lmin是Lu中的最小值；μu是分段函数，表示特征值u的权重，其取值在[0,1]。

(4)背景加权的目标直方图建模

(11)

其中：μu为背景加权系数，C′为归一化因子。

(5)Bhattacharyya公式

(12)

2.3 Kalman预测滤波器

Kalman预测滤波算法是根据目标的历史运动数据来预测目标下一时刻运动轨迹的一种跟踪方法。本文使用目标的位置和速度信息作为Kalman预测滤波器的状态参数，由于图像序列中相邻两帧图像之间的间隔时间较短，两帧之间速度的变换量较小，所以假设图像序列中的目标做匀速运动。则卡尔曼滤波器的状态方程定义为：

(1)状态预测方程

x(k|k-1)=Ax(k-1|k-1)，

(13)

x(k|k-1)是根据k-1时刻的目标状态预测k时刻的状态信息，x(k-1|k-1)是目标k-1时刻的状态信息，A是状态转移矩阵，本文中的状态信息x为：

x=[x,y,vx,vy]T，

(14)

其中：x,y分为表示目标在图像中的横坐标和纵坐标，vx和vy分别表示目标的横向运动速度和纵向运动速度。状态矩阵A为：

(15)

(2)协方差预测方程

P(k|k-1)=AP(k-1|k-1)AT+Q，

(16)

其中：P(k|k-1)为根据k-1时刻预测到k时刻的协方差，Q为测量噪声方差。

(3)Kalman增益方程

Kg(k)=P(k|k-1)HT/
(HP(k|k-1)HT+R)-1

(17)

Kg(k)为k时刻的卡尔曼增益值，H为观测矩阵，R为过程噪声方差。

(4)协方差更新方程

P(k|k)=(I-Kg(k)H)P(k|k-1)，

(18)

P(k|k)为修正后k时刻的协方差值。

(5)状态更新方程

x(k|k)=x(k|k-1)+
Kg(k)(Zk-HX(k|k-1))，

(19)

x(k|k)为修正后的状态信息，Zk为观测到的目标状态信息

(20)

H为观测矩阵，本文H的取值为：

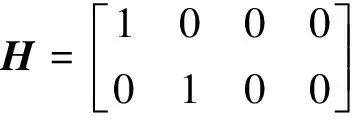
(21)

2.4 融合HRBW Mean Shift和Kalman预测滤波器

Bhattacharyya系数法可以用来衡量目标模板和候选模板之间的相似度，其值在[0,1]之间，Bhattacharyya系数值越大，表示候选模板与目标模板越相似。当目标正常跟踪时，巴氏系数值在某一范围内波动；当目标被遮挡时，巴氏系数值急速下降。所以本文中使用巴氏系数作为跟踪时的遮挡检测方法，设定遮挡阈值为Bh。融合HRBW Mean Shift和Kalman预测滤波器的方法进行目标跟踪时的步骤如下所示：

(1)对目标进行初始化，使用矩形框选定目标，根据公式(1)对目标进行初始建模，根据公式(8)对目标框外的背景进行建模，根据公式(10)得到背景加权系数，然后使用公式(11)建立基于直方图比的背景加权的目标模型。

(2)获取下一帧图像数据。

(3)根据公式(5)获取目标当前的位置信息y1，并开始迭代。

(4)若‖y1-y0‖<ε或迭代次数k>n，迭代停止，根据公式(12)计算Bhattacharyya系数值ρ′(y)，并将当前目标的位置信息传给Kalman预测滤波器。

(5)若ρ′(y)>Bh，则继续使用HRBW Mean Shift算法进行跟踪，重复步骤2、3、4、5，若ρ′(y)

(6)使用Kalman预测的公式(19)更新目标的当前位置。并计算当前帧的Bhattacharyya系数值ρ′(y)，重复步骤5。

3 结果讨论和分析

图2 a组图像序列的相似度曲线对比图Fig.2 Comparison diagram of similarity curves of group a image sequences

本文在Windows平台下的Visual Studio软件下验证上述算法的有效性，设定遮挡阈值Bh=0.5。分别使用两组(a组和b组)带有遮挡物的图像序列来验证本文算法的遮挡跟踪性能。图2为a组图像序列中跟踪运动目标时的相似度值曲线对比图。在目标正常跟踪时，本文算法相对Mean Shift算法的相似度值减小了不超过0.06，不影响目标的正常跟踪。在遮挡情况下，图中使用Mean Shift算法在完全遮挡时的Bhattacharyya系数值为0.55(目标经过遮挡物后跟踪算法失效，所以Bhattacharyya系数值保持在0.55)，Bhattacharyya系数值始终大于遮挡阈值Bh，所以此种情况下使用Mean Shift算法中的Bhattacharyya系数法无法判断目标的遮挡状态，目标进入遮挡时无法启用Kalman预测滤波器，跟踪失效。使用本文跟踪算法跟踪目标时，目标被完全遮挡时Bhattacharyya系数值为0.38，相对于Mean Shift算法中的Bhattacharyya系数的临界值减小了0.17。此时巴氏系数值小于遮挡阈值Bh，故本文算法可以判定此种情况的遮挡状态，及时启动Kalman预测滤波器进行预测跟踪。其跟踪效果如图3所示。

图3 a组图像序列踪效果图Fig.3 Picture of tracking in image sequence of group a

飞机在进入云层中(如图220帧)被判定为遮挡状态，此时启动Kalman预测滤波算法进行预测跟踪，如图230帧和240帧，250帧和260帧表示目标离开遮挡物后切换到跟踪算法进行跟踪。图4为b组图像中跟踪运动目标时相似度值的曲线对比图，由图可知，在遮挡阈值为0.5时，本文算法和Mean Shift算法均能检测出遮挡。本文算法在272帧图像中检测出遮挡，而Mean Shift算法在278帧才检测出，本文算法相对Mean Shift算法提前检测出了遮挡，因此更加及时的启用了Kalman预测滤波器。Mean Shift跟踪算法在272～278帧的遮挡过程中，由于目标的特征信息被遮挡，使用跟踪算法获取的目标位置和真实位置有偏差，若将此偏差传入到Kalman预测滤波器中，特别是偏差较大时，会使得预测失效，所以及时地启动Kalman预测滤波器有利于提高遮挡时的跟踪性能。灰度图像序列在遮挡时的跟踪效果如图5所示。

图4 b组图像序列的相似度曲线对比图Fig.4 Comparison diagram of similarity curves of groupb image sequences

图5 b组图像序列跟踪效果图Fig.5 Picture of tracking in image sequence of groupb

4 结 论

本文针对遮挡跟踪时使用Mean Shift算法和Kalman预测滤波器融合的方法时因遮挡判定不准确而造成跟踪失效的缺点，提出使用基于直方图比的背景加权的Mean Shift算法和Kalman预测滤波器融合的方法，基于直方图比的背景加权的Mean Shift跟踪算法通过来改进目标模型来减少初始化跟踪框中的背景像素的影响，进而提高遮挡判定的准确性。通过实验表明，使用基于直方图比的背景加权的Mean Shift算法和Kalman预测滤波器融合的方法能够有效判定目标的遮挡状态，并在目标被遮挡的情况下进行连续的跟踪。此方法可在FPGA硬件平台上实现高帧频跟踪，具备一定的工程实用价值。 由于Kalman滤波方法适用于线性运动的目标或在遮挡时间较短的情况下，后续工作中将针对非线性运动目标进行研究，并解决目标遮挡时间较长的遮挡跟踪问题。