基于helmert的光雷数据融合处理方法
2019-03-26王春阳刘少英
王春阳, 刘少英,张 月
(中国白城兵器试验中心,吉林 白城 137001)
1 引 言
随着我国武器系统的快速发展,靶场试验任务对测试设备的要求越来越高[1]。光电经纬仪作为飞行目标外弹道测量的主要手段,具有精度高、直观性强等优点,但只能提供目标的角度信息[2]。雷达可以提供较高精度的测距信息,但测角精度较低[3]。为充分发挥经纬仪和雷达各自的优点,近年来,部分靶场将光电经纬仪和雷达联合起来对同一飞行目标进行跟踪测量,事后将雷达的测距数据和经纬仪测角数据进行融合,实现联合交会定位[4]。
20世纪70年代初,数据融合的概念被提出,它是指将多种技术手段给出的测量信息融合处理,以获得目标参数的精确估值[5]。目前,国内相关机构对雷达光电经纬仪多站交会方法进行了大量研究[6-8]。文献[6]根据角度、距离观测值与目标空间坐标的几何关系,建立观测方程,并对其线性化,得到平差模型。文献[7]将样条约束方法应用于角度、距离和速度测量数据的融合处理。文献[8]利用经纬仪测角信息和附近的雷达测距信息进行融合,得到目标相对于雷达的方位角和俯仰角,从而确定目标的空间位置。上述研究的方法均将经纬仪的测角数据和雷达的测距信息一同加入到解算模型中,充分利用经纬仪和雷达各自的优势,提高了目标的定位精度。但在处理方法上存在一些问题,如文献[6]和[7]的方法只建立了函数模型,并未考虑随机模型,角度观测值和距离观测值单位不同,属于不同类型的观测量,难以估计他们的方差,从而不能精确定权。而文献[8]本质上并没有采用交会的算法,得出的结果仅比雷达单台定位精度高,并且可靠性较低。
如何在联合平差中合理地确定不同类观测值之间的权比,是数据融合处理的关键。处理这类问题的一般方法是根据仪器出厂标明的精度估算各自的方差,从而定权,但实践证明,这种方法是不够精确的[9]。因此,许多学者将验前定权改为验后定权,提出了方差分量估计法,它是通过迭代计算,对不同类的观测值进行重新定权,使他们的单位权中误差最大限度趋于一致,从而使权的分配更加合理[10]。
为了能更好地发挥雷达和光电经纬仪各自的优势,使两者采集的数据能更好进行融合,进而获取精度更高的弹道三维坐标,本文提出了两种雷达光电经纬仪联测数据处理方法。针对角度观测值和距离观测值属于不同类型的观测量,难以精确定权的问题,引入了基于方差分量估计的多站交会方法;为了解决方差分量估计法处理结果中出现的“尖刺”,提出了将最小二乘多站交会与Helmert方差分量估计结合的处理方法。最后,通过对算例数据进行分析及验证,证明本文方法的可行性和有效性。
2 原理及数学模型
2.1 雷达、光电经纬仪交会测量模型
如图1所示,靶场坐标系为O-XHZ,光电经纬仪和雷达的测量值分别为方位角Ai、高低角Ei及距离Ri。根据几何投影关系可以得到下列关系式[11]:
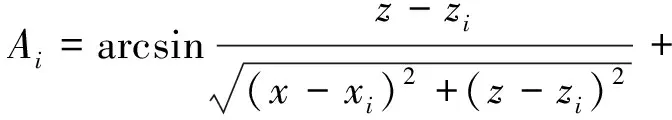
(1)
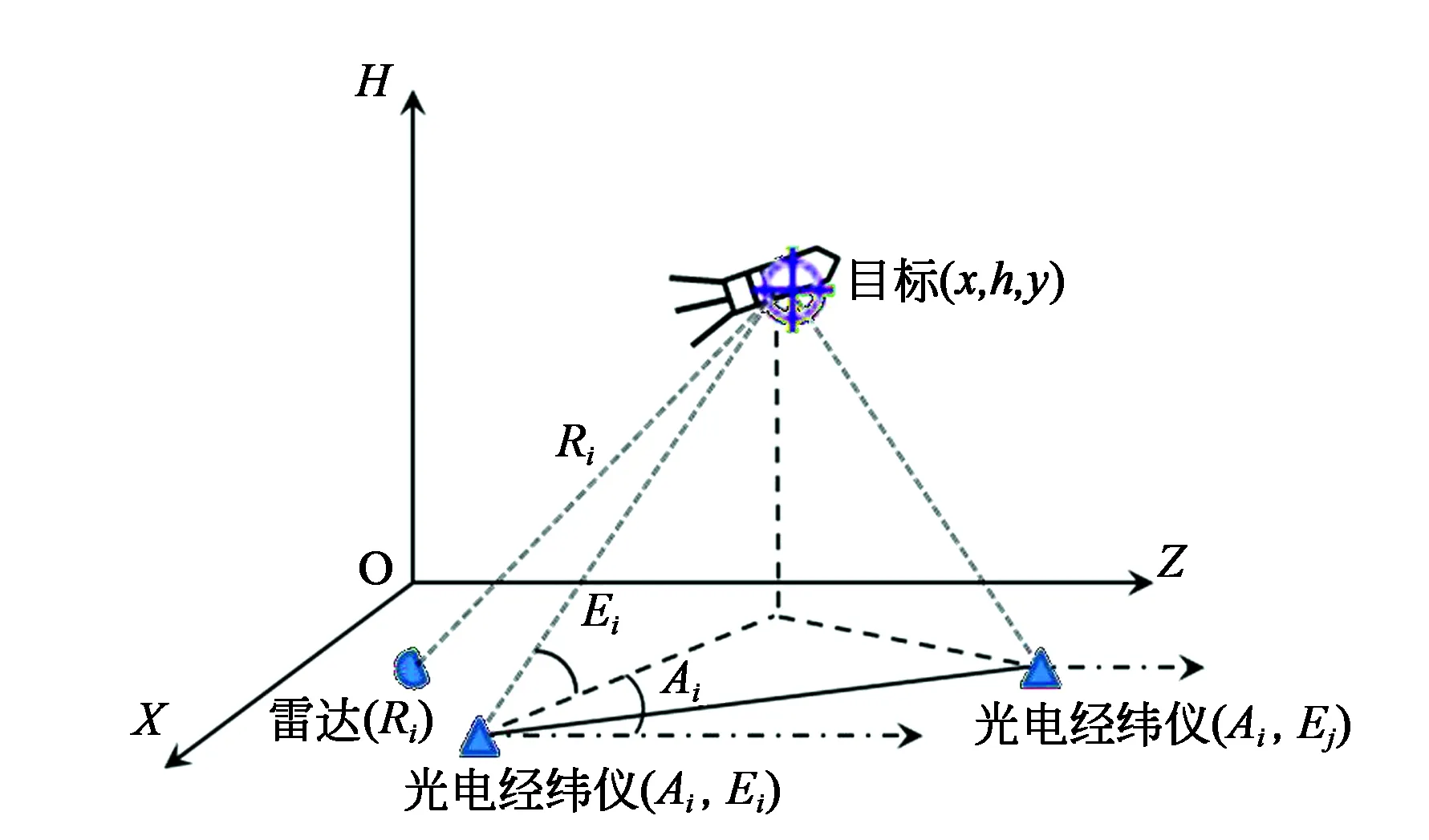
图1 雷达、光电经纬仪与飞行目标的关系Fig.1 Relationship between radar、 photoelectric theodolite and flight target
(2)
(3)
由于公式(1~3)是非线性方程,需要做线性化处理,对公式(1~3)在初值(x0,h0,z0)处做泰勒级数展开,省略二次以上的高阶项,建立误差方程:
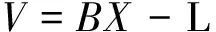
(4)

系数矩阵为:
Li=(x0-xi)2+(z0-zi)2;
Ri=(x0-xi)2+(h0-hi)2+(z0-zi)2.
由高斯-马尔可夫估计得[12]:
(5)
参数向量协方差阵为:
PX=(BTPB)-1,
(6)
得出炸点坐标为:
x=x0+δx,y=y0+δy,z=z0+δz.
2.2 Helmert方差分量估计模型
由上述的模型可以看出,观测值分两类,光电经纬仪的测角观测值和雷达的测距观测值。假设两类观测值之间相互独立,其权阵分别为P1、P2。建立误差方程为:
(7)
(8)
式中:V1、V2、B1、B2、L1、L2代表的含义同公式(4)。

两类观测值的Helmert方差分量估计公式为:
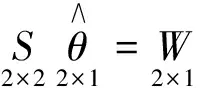
(9)
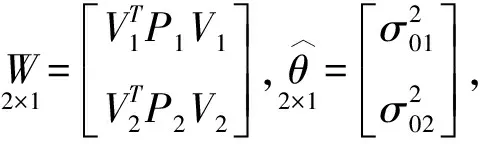
m1和m2为测角观测值数和测距观测值数。
(10)
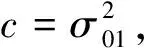
3 算例与分析
3.1 数据与实验
依据质点运动方程在靶场坐标系下推算一条理论弹道,用弹道三维坐标反推设备观测数据,采样间隔为0.1 s,全弹道采集925个历元。假设设备可以对弹道进行全程跟踪测量。选取3台光电经纬仪和4台雷达,每个历元可以获得10个观测数据,分别为4台雷达的4个测距数据和3台经纬仪的6个测角数据,依据设备实际精度,在测元数据中加入随机误差(角度误差为40 s,距离误差为1 m),设备与弹道轨迹的几何关系如图1所示,其中,3台光电经纬仪和4台雷达均布设在弹道左侧。
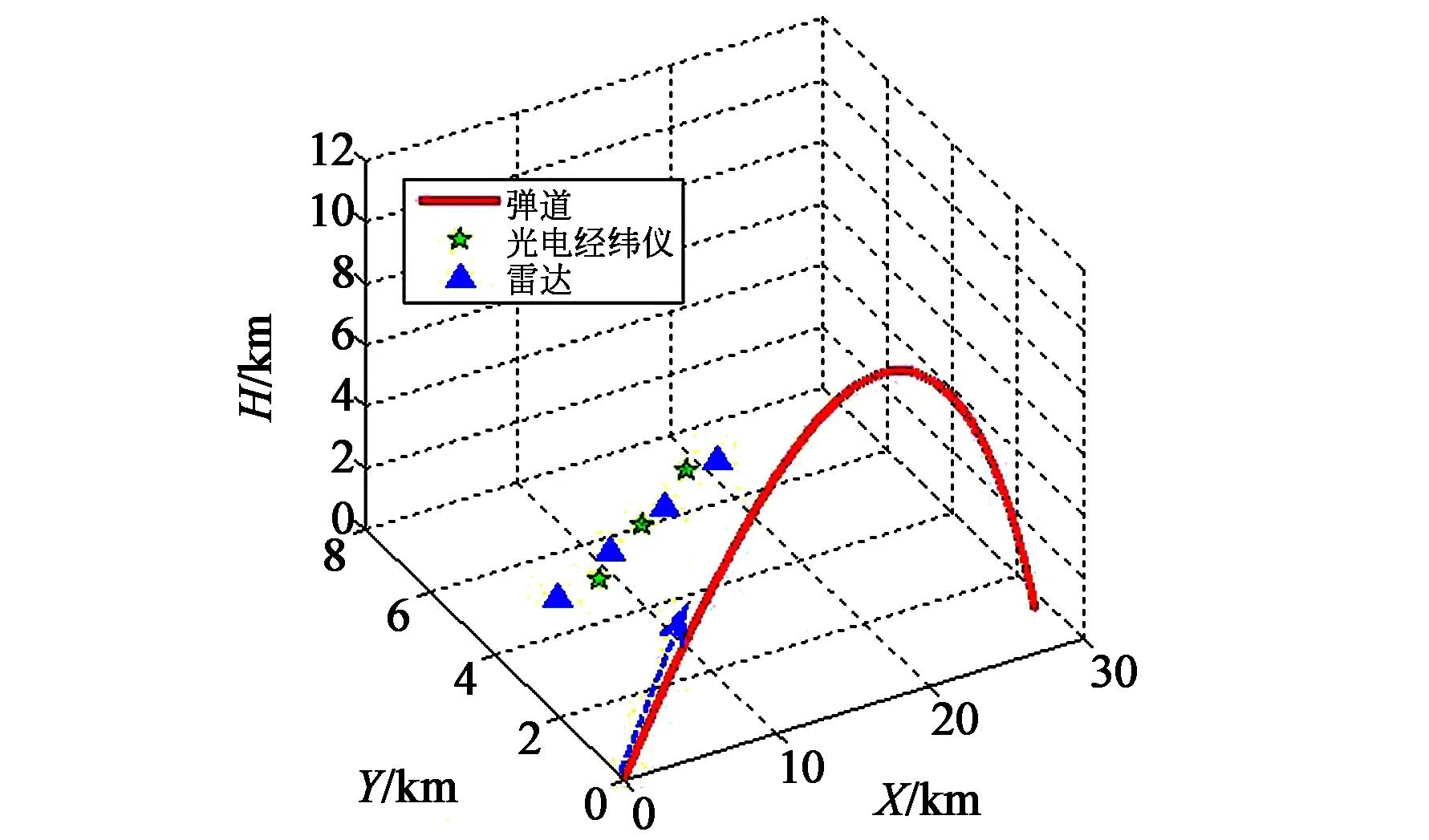
图2 雷达、光电经纬仪与弹道的空间几何关系。Fig.2 Space geometric relationship between radar,photoelectric theodolite and trajectory
3.2 观测值不含粗差
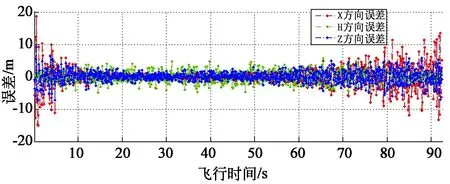
图3 采用最小二乘多站交会法计算的误差曲线Fig.3 Error curve calculated by the least square multi station intersection method
首先,采用基于最小二乘估计的多站交会法对3台光电经纬仪的测角数据进行计算,结果如图3所示,解算误差在弹道的起始段(0~20 s)和末段(60~90 s)明显大于中间段(20~60 s)。这是由于解算结果除了受设备测量精度影响外,还与布站几何有关,通常用几何精度因子GDOP来描述定位精度与布站几何之间的关系,其值越大,说明定位精度越低。GDOP计算公式为[15]:
(11)
用公式(11)计算弹道上每个测量点处的GDOP值,结果如图4所示,可以看出,GDOP的变化趋势与图3中的误差变化趋势相一致。当目标处于弹道起始段和未段时,X方向误差较大,达到10 m以上,而H方向相对稳定,始终维持在±3 m。说明H方向的精度受布站方式的影响小于其他方向。
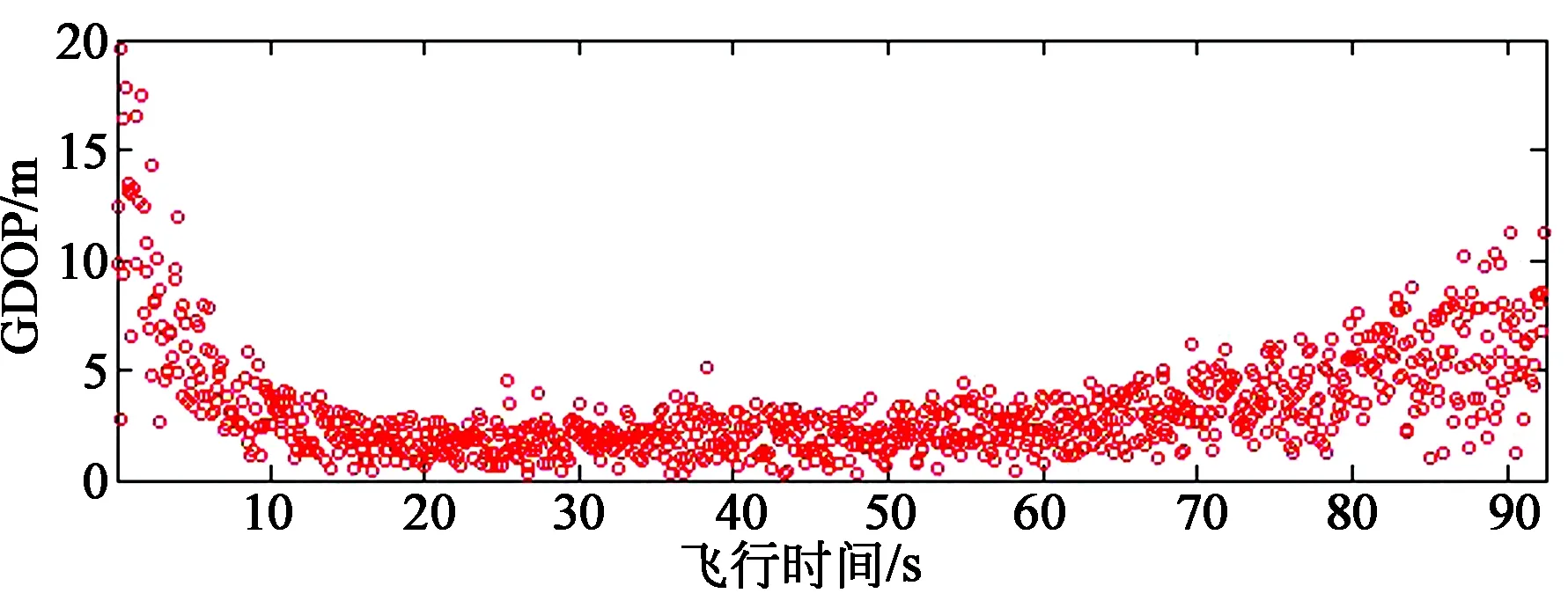
图4 弹道不同位置处的GDOP值Fig.4 Value of GDOP at different positions of the trajectory
然后,采用Helmert方差分量估计法对雷达、光电经纬仪的测角、测距数据进行融合,解算全弹道各个历元的三维坐标,误差如图5所示。
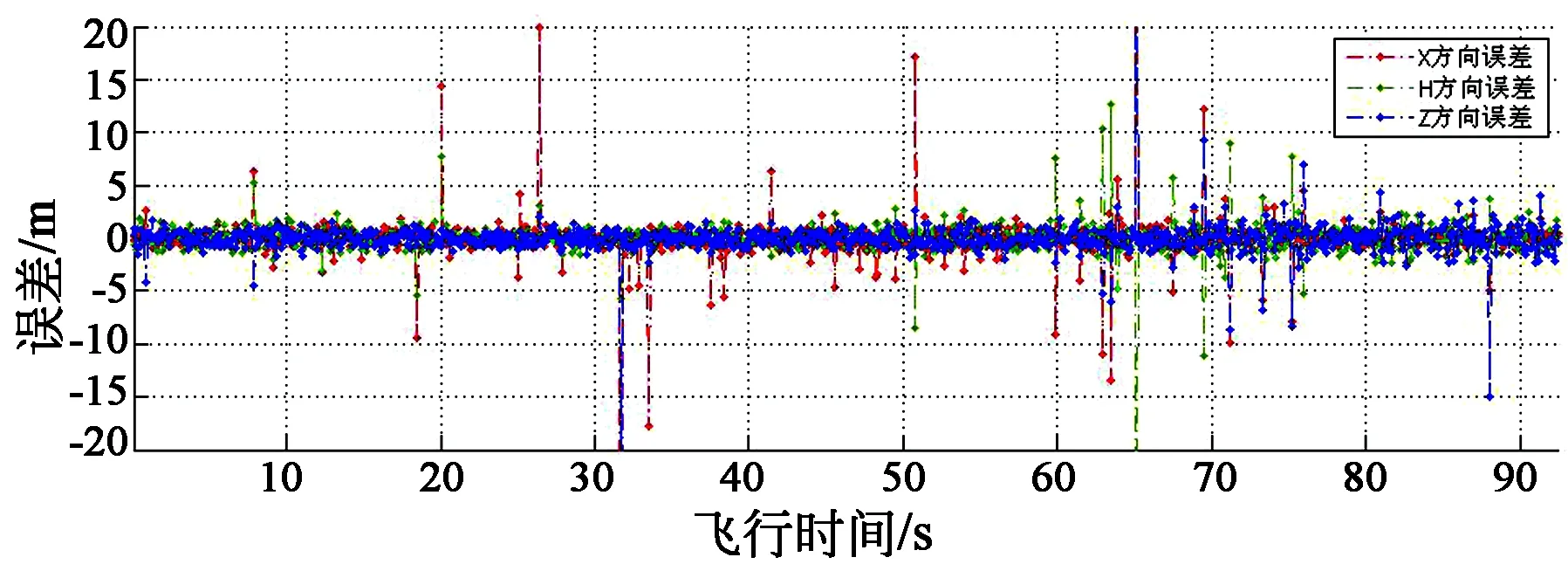
图5 Helmert方差分量估计计算的误差曲线Fig.5 Error curve calculated by Helmert variance component estimation
从图5可以看出,方差分量估计不受布站几何影响,每个历元处的解算精度趋向稳定,除个别点出现“尖刺”外,总体上误差基本在5 m以内。对出现“尖刺”处的数据进行进一步分析发现,在方差分量估计过程中,单位权方差估值出现了负值,计算每个历元处S矩阵(公式9中的矩阵)2范数下的条件数[16](一般认为0~100以内性能较好,而大于1 000性能较差,可认为是病态矩阵)。结果如图6所示,可以发现“尖刺”出现的时刻与条件数较大的时刻一致。因此可以证明由于S矩阵出现病态,致使单位权方差估值出现了负值,影响了解算精度。而S矩阵的病态性产生的原因可能是模型矩阵的列向量间存在复共线性关系,这会导致最小二乘估计结果变得不稳定[17-18]。
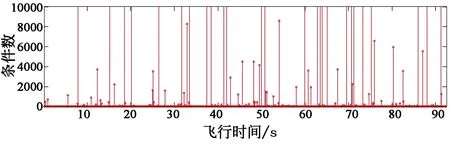
图6 S矩阵2范数下的条件数Fig.6 Conditional number under the 2 norm of S matrix
针对S矩阵病态的问题,可采用有偏估计法对其进行处理,但是岭参数的确定是非常困难的,目前没有公认的好办法[19]。本文提出了一种相对简单的处理方法,即采用最小二乘多站交会法与Helmert方差分量估计法相结合法,这种方法的处理思路是,有“尖刺”的历元数据用前者解算,其他时刻数据用后者解算。具体处理方法是,首先按照Helmert方差分量估计法处理,发现单位权中误差为负值时,将P2设置为零矩阵,即除去雷达测距信息对参数估计的影响。采用此方法的解算误差如图7所示。
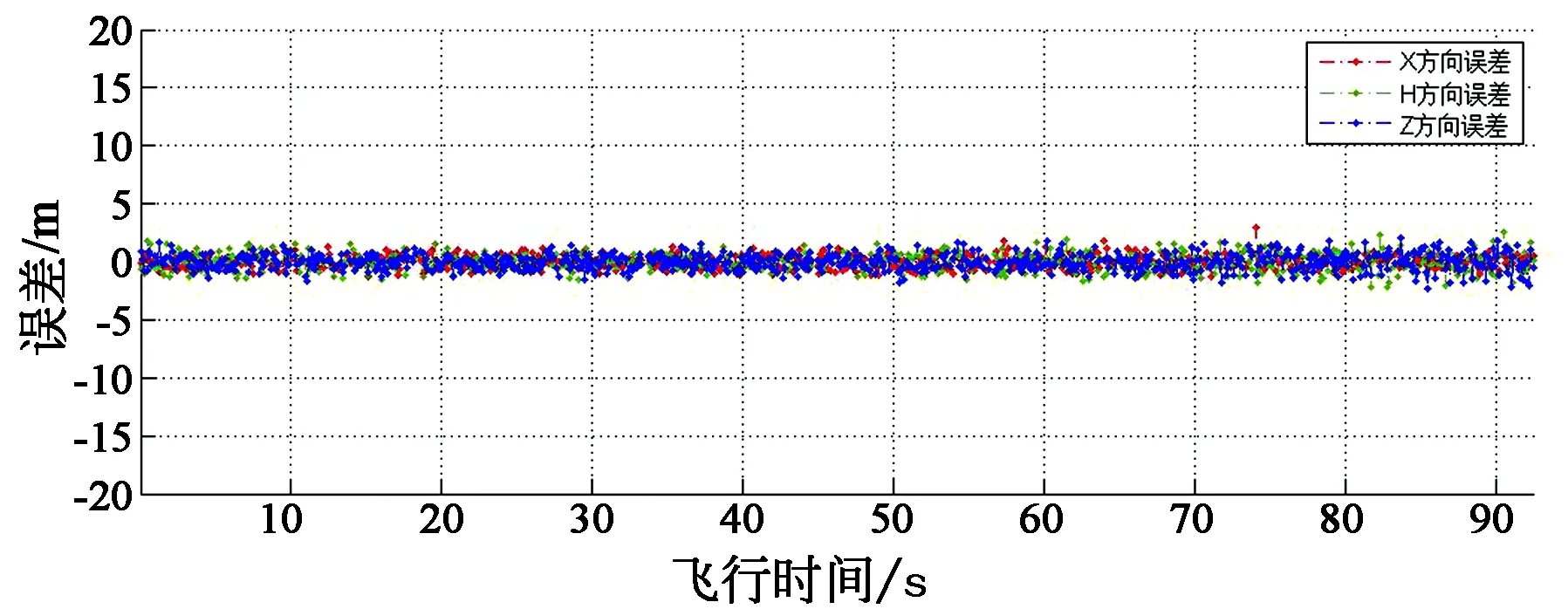
图7 两种方法结合计算的误差曲线Fig.7 Error curve calculated by the combination of the two methods
对比图5、7误差曲线,可以看出,两种方法结合,可以取各自的优势,达到理想的效果。这种处理方法计算简单、容易实现,不但能较好地解决“尖刺”问题,而且不受布站几何影响,提高了解算精度的同时,也提高了误差变化的稳定性,精度基本控制在5 m以内。
表1为3种方法解算结果的均方根RMS,对比发现,方差分量估计法受“尖刺”影响,总体精度下降很多,变得不稳定;而最小二乘多站交会法在起始段和末段精度较差,也不稳定;将两种方法相结合,解算精度在X、H、Z方向均小于1 m,明显优于分别处理的结果。
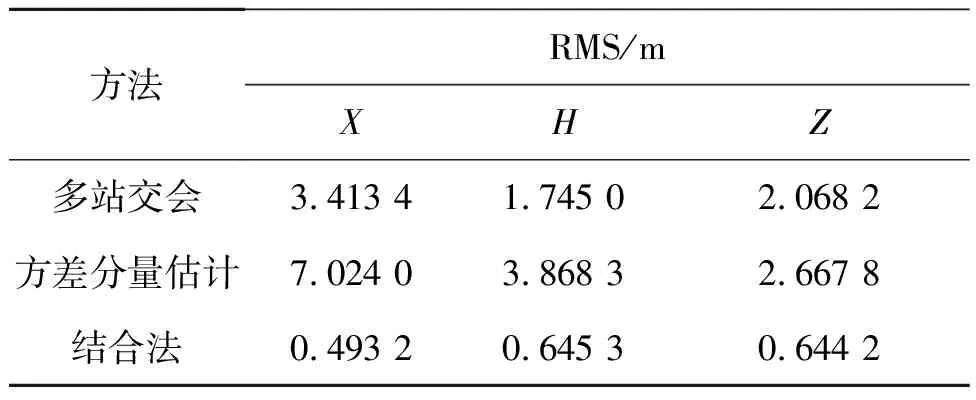
表1 不同方法解算结果的均方根Tab.1 RMS results of different methods
3.4 结果
对算例进行分析可以总结出:
(1)基于最小二乘估计的多站交会法受布站几何影响较大,当GDOP值较高时,微小的误差也会对参数估值产生较大的影响,而Helmert方差分量估计法利用雷达测距信息能有效改善这种影响。
(2)Helmert方差分量估计法存在一个问题,在估计过程中,单位权方差估值经常出现负值,致使误差曲线呈现一定数量的“尖刺”,“尖刺”的位置与单位权方差出现负值的位置一一对应。
(3)将最小二乘多站交会法与Helmert方差分量估计法结合,取两种算法各自的优点,不但可以有效降低布站几何的影响,又能去除“尖刺”,该方法在X、H、Z方向的解算精度均小于1 m。
(4) 当观测值中只含有角度信息时,可靠性指标受布站几何影响较大,观测值中较小的误差会对参数估值产生很大的影响,尤其是水平角,影响更为明显。
(5) 造成Helmert方差分量估计产生“尖刺”的原因是S矩阵呈现病态,模型矩阵的列向量间存在复共线性关系。
4 结 论
通过算例数据对基于Helmert方差分量估计、最小二乘多站交会与Helmert方差分量估计相结合两种方法进行了分析和验证。结果证明:最小二乘多站交会与Helmert方差分量估计结合法,受布站几何的影响较小,还可以去除“尖刺”现象,在X、H、Z方向上的解算精度均小于1 m。
