梯形透水潜坝附近水面线及透水率
2019-03-26王文森程永舟王小明黄筱云
王文森,程永舟,2,王小明,黄筱云,2
(1.长沙理工大学水利工程学院,湖南 长沙 410114; 2.水沙科学与水灾害防治湖南省重点试验室,湖南 长沙 410114)
随着各种透水结构物的应用日益增多,透水潜坝的水流及透水特性问题也逐渐成为国内外工程界和学术界的研究热点。对于丁坝结构的水流特性问题,国内外学者做了很细致的研究工作[1-4]。透水丁坝相较于传统丁坝对河道的生态环境影响较小,大量学者对于透水潜坝的结构以及水流适用性问题做了应用研究[5-9]。梯形透水潜坝整治效果好,工程造价低,结构安全稳定,水流条件适宜鱼类生存,是同时具备生态修复功能的整治建筑物结构形式。新型梯形透水丁坝结构符合交通部长江南京以下12.5 m深水航道开发项目中“生态型整治建筑物结构研究专项课题”。
透水潜坝的结构透水率及其水流适用性问题是潜坝结构设计及优化的关键问题之一。Kuhnle等[10]采用Doppler流速仪测量了梯形潜坝周围三维流场分布,发现丁坝对岸一侧底部流区纵向流速平缓增加,丁坝侧坝后流区水流流速明显减小,而坝头位置出现逆向的分离区。丁晶晶等[11]将丁坝的实体坝头改成由四面体透水框架铰接而成的透水坝头,认为最优透空率的透水坝头可有效分散集中绕流,减弱脱离涡,阻滞下潜流,控制局部冲刷的效果较好。王普庆[12]通过水槽试验研究了透水桩坝的整治效果以及透水率、来流夹角对于控导河道、缓流促淤的效果。周银军等[13]提出了桩柱式透水丁坝,发现当透水率在20%~30%之间时,坝后回流流速逐渐减小并消失,当透水率继续增大,坝后只产生一个缓流区。在此基础上,宗全利等[14]针对桩柱式透水丁坝的局部冲刷及壅水回流等问题进行了深入研究,确定了坝间距及桩柱直径等关键参数在工程设计中的计算方法。杨元平[15]利用沿水深方向上积分的平面二维水流运动方程组,推导得到透水丁坝坝后回流区长度的计算公式。高先刚等[16]研究发现透水坝后收缩断面至坝头的距离随挑角的增加而增大,随透水率的增加而减小,另外利用无量纲回归分析法得到了坝头附近最大冲刷深度的计算公式。周庆庆等[17]通过物理模型试验,对比分析了不同结构形式的透水丁坝缓流促淤效果,发现透水丁坝结构缓流促淤效果最好,坝头冲刷深度也最小。张凯等[18-19]采取单因素控制变量的方法进行室内动床试验,探索了坝头冲刷坑深度与模型沙粒径、束窄度、流量、水力插板透水率、丁坝挑角之间的关系,并且得出坝头冲刷坑深度与各单因素的回归方程。此外,任志等[20-21]也做了类似的工作,研究了不同含沙量、挑角、流量条件下的水力插板透水丁坝作用区的冲淤规律。对于水力插板透水丁坝的优越性,刘国起做了大量的研究[22]。Yossef等[23]通过定床水槽试验研究了潜坝附近的流场、涡量和紊动能等三维水流特性。王小明等[24]基于OpenFOAM对梯形透水潜坝的三维流场进行了数值模拟,研究了透空率和流量对透水潜坝周围三维水流特性的影响规律。
综上所述,目前对于透水潜坝的研究内容主要围绕四面六边透水框架和框架群及桩柱式透水坝体结构周围水流结构分布;坝头端坡及附近水流结构的调整及影响;潜坝周围冲刷以及透水潜坝工程设计中需解决的关键设计参数等内容展开。鲜有定量考虑结构透水率及其水流适用性的内容。本文基于PIV流场测量系统专用水槽试验与Flow3D数值模拟针对均匀开孔的梯形透水潜坝周围水面线分布及结构透水率与水流特性的关系等问题进行研究,为透水潜坝的推广应用提供理论依据。
1 研究方法
1.1 试验布置及工况
采用概化物理模型开展梯形透空式潜坝周围水面线变化及透水特性的研究。试验在长沙理工大学水利实验中心PIV专用水槽中进行。水槽长16 m、宽0.4 m、高0.5 m,试验水深0.15~0.35 m。水槽造流由计算机控制流量变化,水槽尾部设置格栅尾门以调节水位。流速测量采用SoPtek公司的超声多普勒流速仪进行。水槽采用水泵供水,梯形透空式潜坝采用透明有机玻璃制成,长B=40 cm,高h=10 cm,顶宽b1=3.5 cm,底宽b2=10 cm。流场测试采用美国TSI公司的PIV系统,其中光源为双脉冲激光,采用强激光(约为120 mJ)以保证所测区域被均匀照亮。由同步器控制触发,采集频率为1.04 Hz;PIV系统通过双曝光相机拍摄图像并传输到IPsight3G后处理系统进行计算处理。图像采集间隔为100 μs。测量区域为200 mm×200 mm,试验前对仪器进行标定。根据PIV水槽造流能力及尺寸进行试验布置,如图1所示。
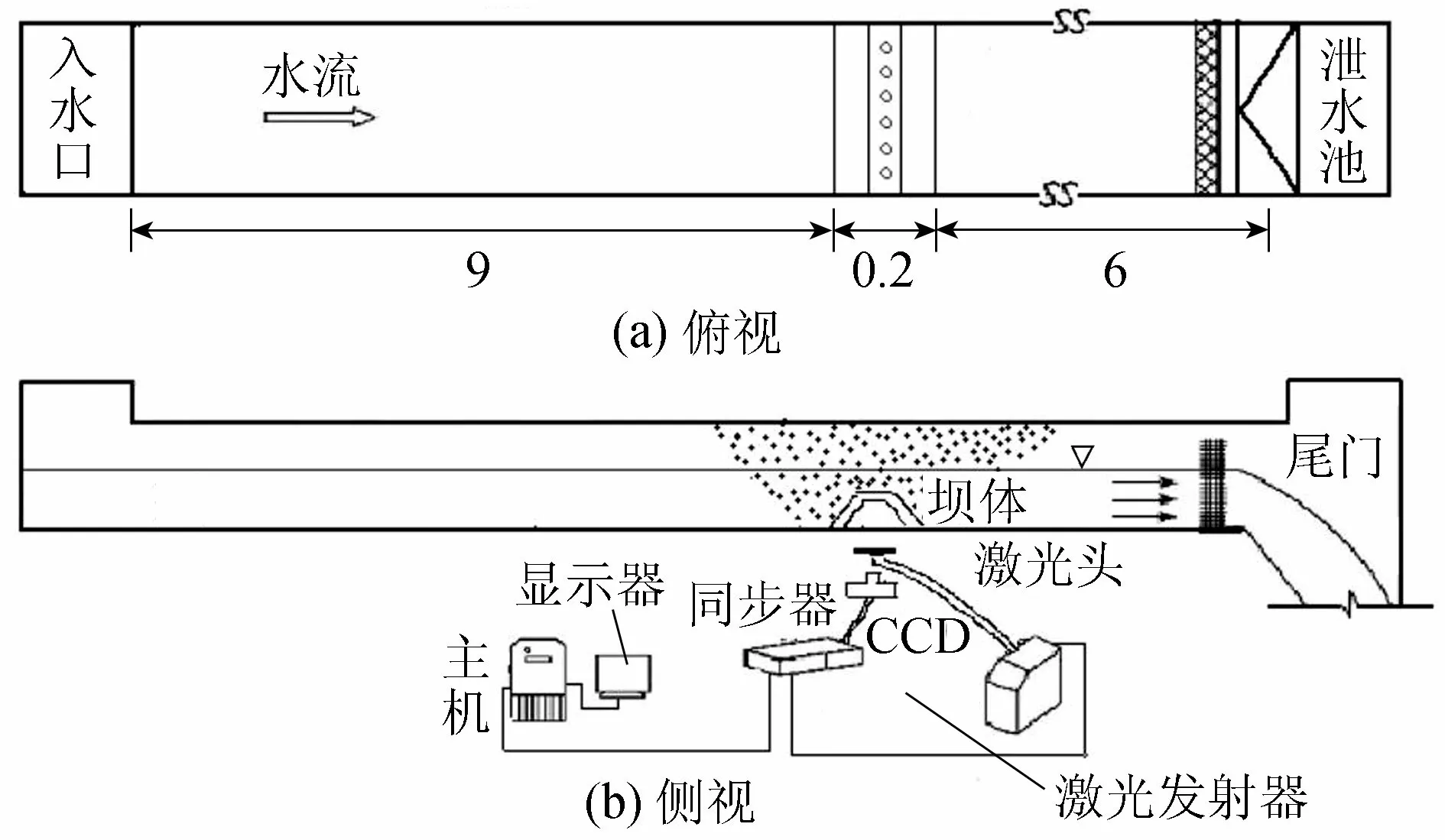
图1 物理模型试验布置(单位:m)
试验中考虑到水槽边壁对水流的影响,采集数据时只取了中间3个断面。最后确定试验水流比尺为1∶50,水槽宽度为0.4 m。试验设置工况组次见表1。
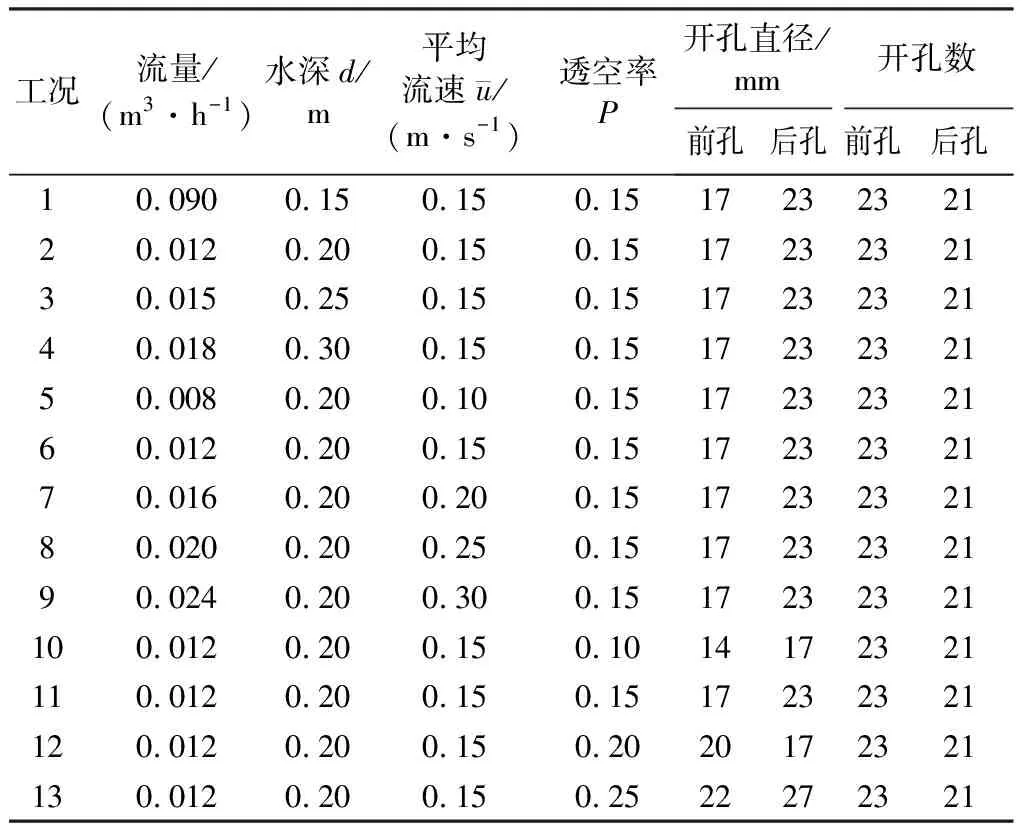
表1 试验水槽及潜坝模型参数
1.2 数值模型建立及验证
1.2.1 数值模型建立
本文采用Flow3D进行数值模拟。数值计算中N-S方程通过有限体积法进行离散,计算网格利用Flow3D独有的FAVOR网格处理技术进行解析。计算区域被分解成无数个体积元,即单个控制体。以通量形式存在的偏微分方程在不同体积元之间相互联系。而联系中所涉及的量值均保存在体积元质心,相邻质心间的区域物理量以差值法确定。方程求解采用SIMPLE算法实现流体速度解耦,时间离散采用Euler格式。自由液面模拟是采用流体体积法(VOF)精准捕捉自由面而实现。具体的VOF方程:
(1)
式中:α为液体在计算网格中所占的体积比例;t为时间;为哈密顿算子;ui为相对速度;最后一项·[uiα(1-α)]为人工压缩项。α=1表示液体,α=0表示气体,α介于0和1之间表示该网格为气液交界面。控制方程为连续性方程和黏性流体的N-S方程,具体表达式如下:
(2)
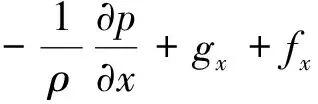
(3)
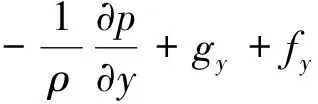
(4)

(5)
式中:u、v、w分别为x、y、z方向的速度;Sx、Sy、Sz分别为x、y、z方向的可流动面积分数;ρ为流体密度;Vi为可流动体积分数;gx、gy、gz分别为x、y、z方向的重力加速度;fx、fy、fz分别为3个坐标轴方向的黏滞力;p为压强。
数值模拟水槽同物理水槽尺寸一样。为节省计算资源,数值模型选取水槽中坝前1 m,坝后2 m作为计算区域(图2)。水槽底部及边壁和透空潜坝表面为固壁无滑移边界。两侧面采用对称边界,通过简化模型将网格数目降低到原来的一半,而在后处理时利用模型对称性还原整体模拟结果。入水口采用固定流速,出水口设置为固定水深恒压自然出流。数值模型整体采用分区多块渐变式网格。考虑到水流为恒定单向流,数值水槽采用求解精度较高的边长小于1 cm的六面体结构化网格进行划分。而对透空潜坝复杂结构附近则采用网格划分工具以边长为5 mm的结构化网格进行加密填充。同时潜坝表面设置边界层网格,以保证其附近流场求解的精确性。为保证数值计算的稳定性,潜坝附近至水槽其他区域网格密度渐进变化。数值水槽上边界恒定来流、下边界恒压出流,并按坝前附近的断面平均流速为控制条件。
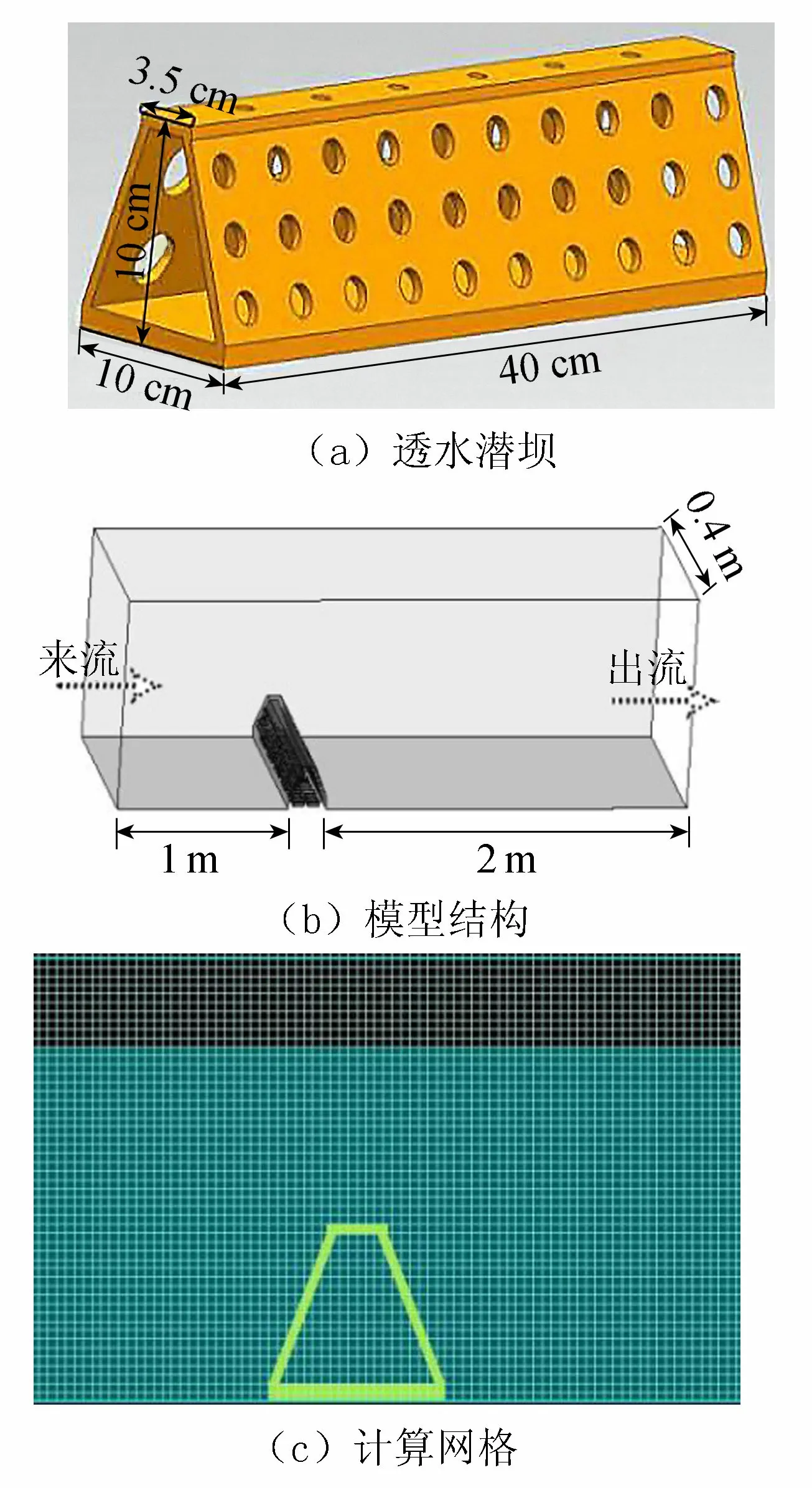
图2 数值模型结构及网格
1.2.2 数值模型验证
选取长0.4 m、高0.1 m、透空率为0.15的模型,在工况1和工况2两种工况条件下进行数值模型验证。通过对比以上两种工况条件下水槽水流试验段坝前、坝上和坝后3个位置的垂线流速分布,得到垂线流速分布验证结果如图3和图4所示(图中高程以水槽底为零点,下同)。由图3和图4可知,数值计算结果与试验水槽实测垂线流速吻合较好,两者间最大误差小于5%,证明该三维数值模型可以较好地模拟透水潜坝周围三维流场。
2 结果分析
2.1 水面线变化特性
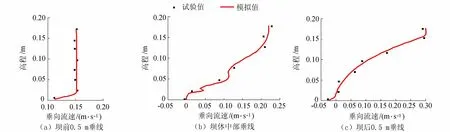
图3 工况1水槽中轴线上各点垂向流速验证
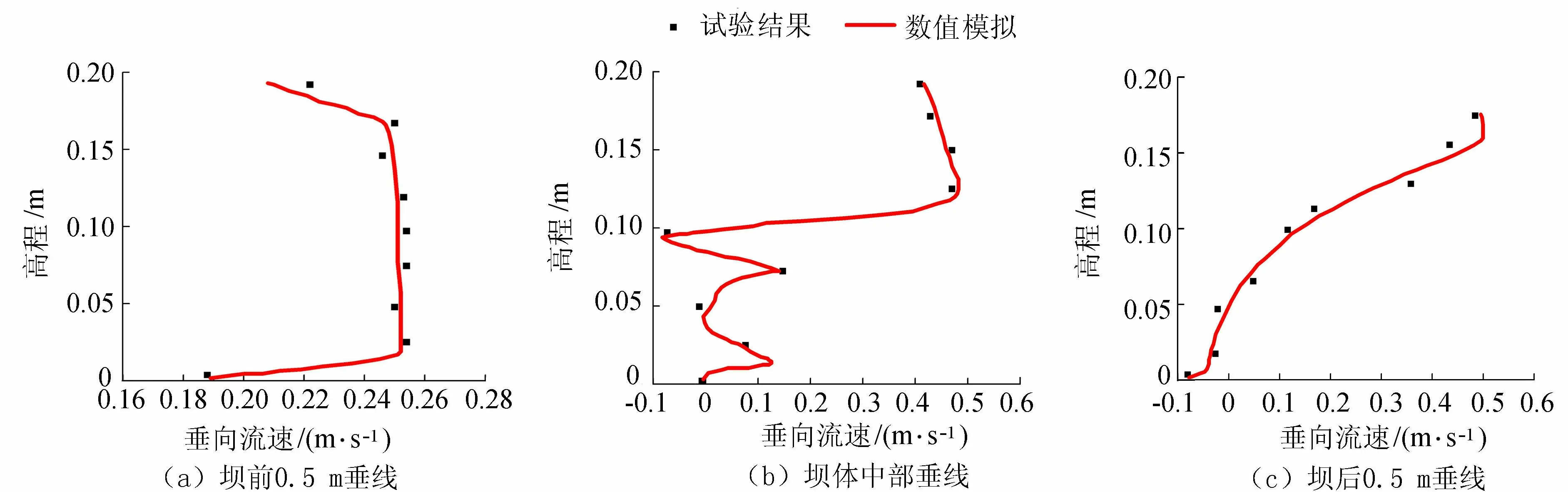
图4 工况2水槽中轴线上各点垂向流速验证
水深对水面线的影响如图5所示。由图5中4种水深条件下水面线图可知,水深为0.15 m和0.20 m工况的水面线坝后略有水跌。特别是潜坝坝前远端水深为0.15 m时,坝后由于坝体结构透水性弱,断面平均流速最大,水跌高度最大。水深为0.25 m和0.30 m的潜坝附近水面波动较小,潜坝附近水面壅水及水跌高度随水深增大而逐渐减小。这是由于当水深逐渐增大时,翻坝的坝上流量也在增大。而坝后由于水深较大,翻坝水流能量迅速耗散,水体恢复平静,水跌高度下降,水面线更加平稳。水深越大,同一坝体附近水面线变化幅度越来越小,坝前水位壅高及坝体附近水跌均逐渐消失。
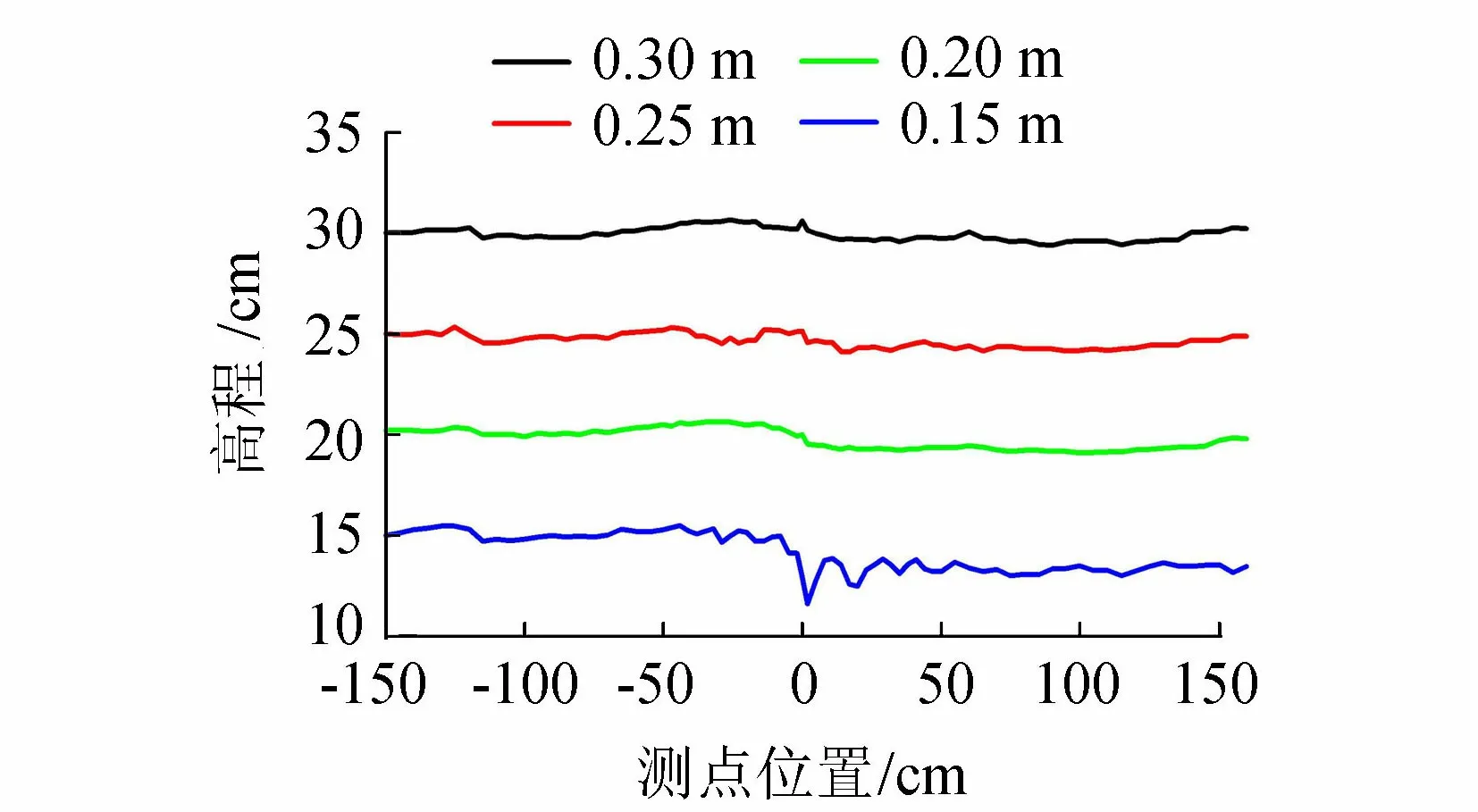
图5 不同水深的水面线形状

图6 不同透空率对水面线的影响
透水率对水面线的影响如图6所示。根据图6,在平底水槽中透水潜坝坝前及坝后分别形成了两个水面逆坡。坝前由于远端水深控制为0.2 m,而坝后逆坡是在潜坝影响了水体行进,发生壅水。随后由于坝体前后水位差形成的势能转化为流速之后,能量迅速耗散,水深随之增大,坝后逆坡比坝前逆坡坡度更大。对比不同透空率的潜坝结构附近水面线变化规律,发现随着透空率增大,壅水及水跌高度逐渐减小。这是由于当潜坝透空率增大时,透过坝体的流量也在增大。坝后水量增大后,水位迅速恢复,水跌高度自然下降。相同水流条件下,不同透空率的梯形潜坝坝后水面均出现了“逆坡”且坡度基本相同。随着潜坝透空率增大,不同坝体附近水面线整体变化幅度不大。坝体前后水跌高度大都在1~2 cm范围内,而坝前水位壅高值均在1 cm以内。
断面平均流速对水面线的影响如图7所示。根据图7,当控制坝前远端水深和潜坝透空率不变,逐渐增大断面平均流速时,潜坝结构附近水面线壅水及水跌高度随着断面平均流速增大而逐渐增大。这是由于当坝前远端水深一样的情况下,随着断面平均流速逐渐增大,翻坝的坝上流量也在增大,而断面面积在坝上区域又逐渐减小,坝上水体流速迅速增大。翻坝水体由于势能转化为动能流速较大,断面平均流速增大,断面水深降低,水跌高度自然增大。对比不同水面线可以看出随着断面平均流速增大,相同结构坝体的水面线整体变化幅度越来越大。当在水流中设置潜坝后,坝体上游水流也会产生水头损失,但坝前水头损失远不及坝后。坝前水位壅高及水跌幅度增大。坝后水面随着断面平均流速增大,逐渐出现“逆坡”现象,“逆坡”的坡顶和坡底高度差也越来越大。据此可以判断不同断面平均流速的河道水流最为合适的整治潜坝结构透空率,为工程实践提出具体可行的解决方案。
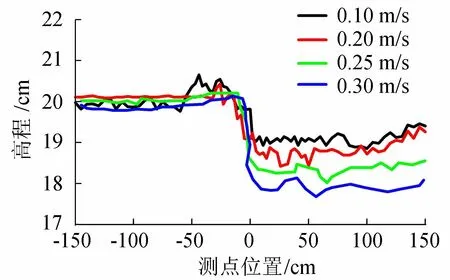
图7 不同断面平均流速对水面线的影响
2.2 潜坝透水率变化特性及公式拟合
2.2.1 潜坝透水率变化特性
2.2.1.1 坝前远端水深对透水率的影响
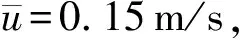
q1=0.008 6d-1.733
(6)
式(6)的相关系数R2=0.996。可以看出同一结构潜坝在相同断面平均流速条件下,随着水深增大,坝体透水率逐渐减小。这是由于水深增大,透过坝体的流量占总流量的比例减小,坝体透水率降低。
2.2.1.2 潜坝透空率对透水率的影响
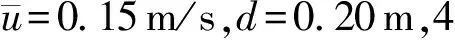
q2=0.082 9lnP+0.294 4
(7)
式(7)的相关系数R2=0.983。在相同水深和断面平均流速条件下,随着潜坝透空率增大,坝体透水率也逐渐增大,但增长速率逐渐减小。透空率增大,潜坝开孔直径增大,透水能力自然增大。而增长速率的减小和潜坝结构前后开孔的交错位置有关,当水体流经交错开孔的潜坝坝体时,水体紊动强度增大,流速减小,坝体透水能力减弱。这一特性的影响程度也会随着透空率增大而表现的更加显著。
2.2.1.3 断面平均流速对透水率的影响
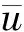
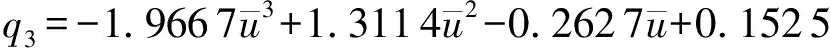
(8)
式(8)的相关系数R2=0.771。可以看出同一坝体结构在相同水深条件下,随着断面平均流速的增大,透水潜坝对水流的分流影响效果基本一样,透水率变化不大。
2.2.2 透水率计算公式拟合
根据上述分析,得到不同透空率、不同水深、不同断面平均流速条件下,梯形透空式潜坝透水率的变化情况。综合潜坝透空率、水深、断面平均流速3种影响因素,采用非线性回归拟合结合量纲和谐化处理,得到梯形透空式潜坝透水率q的综合经验公式为
(9)
采用式(9)在不同工况条件下的计算结果与对应的物模试验结果进行对比,得到如图8的关系曲线,最大误差不超过5%,计算值与实测值吻合较好。
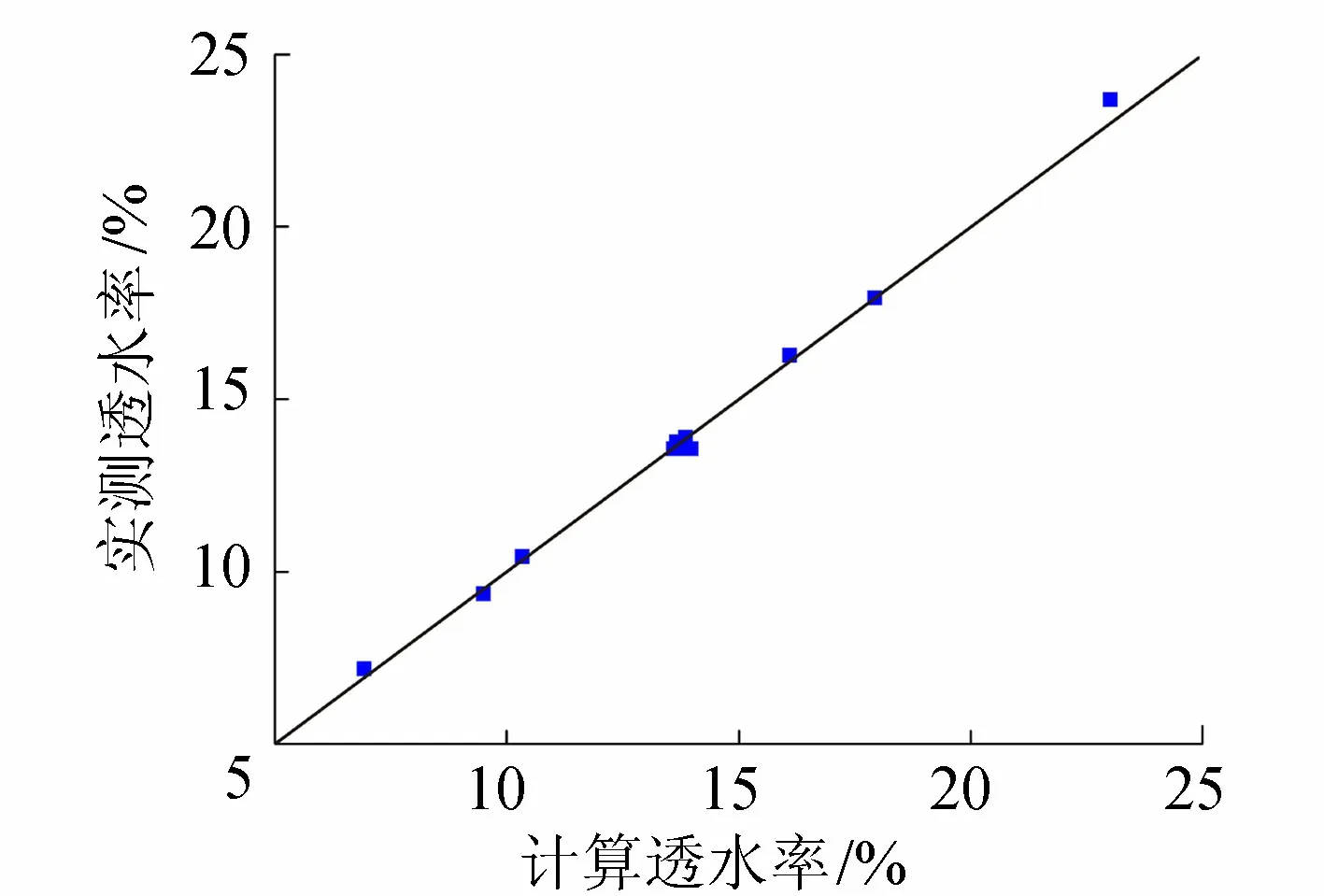
图8 透水率计算值和实测值关系曲线
3 结 论
a. 相同水流条件下,潜坝结构附近水面线壅水及水跌高度随着透空率逐渐增大而减小。不同透空率的梯形潜坝坝后水面均出现了“逆坡”现象。
b. 相同透空率的透水潜坝在同一断面平均流速条件下,水深越大,相对壅水高度越小。当水深约为坝体高度2倍以上时,壅水效果逐渐消失。相同坝前远端水深条件下,随着断面平均流速增大,坝后水跌高度增大。
c. 相同条件下,坝体透空率越大,透水率越大。水深越大,透水率逐渐减小。而断面平均流速对结构透水率影响不大。最后对数据进行非线性回归拟合得到了透水率的综合经验公式,经验证该经验公式计算结果和实测值最大偏差不超过5%,可靠性较好。
