基于二元水循环及系统熵理论的城市用水配置

邹 进

(昆明理工大学电力工程学院水电系,云南 昆明 650500)

水资源优化配置是指在一个特定流域(或区域)内,通过工程与非工程措施,利用系统分析方法、决策理论和计算机技术,统一调配水资源,协调各区域、各部门之间的利益与矛盾,将有限的、不同形式的水资源在各用水户之间进行科学分配,以提高区域整体的用水效率,保障区域水资源的可持续开发利用,促进区域经济社会的可持续发展。在水资源可持续利用框架下,水资源优化配置与水资源承载能力密不可分,水资源优化配置是可持续发展理论的技术手段,承载力分析是可持续发展理论的重要内容,合理的水资源配置将有助于提高水资源的承载能力。

迄今为止,已有大量文献研究了流域(或区域)内的水资源优化配置问题,在模型构建中,一般是将其设置为经济效益最大化[1-2]或水库库容最大[3]、或缺水量最小[4]的单目标优化问题;或是经济、社会、环境效益最大化的多目标问题[5-7]。在求解方法上,普遍采用线性规划法、多目标决策法,近年来也有学者将混沌及熵评价模型[8-9]、 多目标遗传算法[10-11]、大系统分解协调原理[12]等引入其中。

由于城市用水将产生一定量的污、废水,对水资源系统造成了水量需求及水质降低的双重压力。因此,在以水资源可持续利用为目标的水资源优化配置中,应该将水量配置与水环境承载力联合考虑,反映质、量分配的均衡性问题。但总的来看,上述文献中所使用的模型,较少考虑到因配置所引起的水污染问题及其与生态用水之间的关系,也就是说,即使有的文献[5]考虑了城市用水中污水排放量(通常以化学需氧量COD的排放总量表示)的影响,也没有将其与流域水环境的承载能力结合起来,不能反映水资源配置的均衡性问题。因此,本文将利用二元水循环理论,以昆明市为例,在分析城市取用水循环的基础上,建立城市水资源的优化配置模型;并对信息熵进行改进,应用于模型之中,以解决水量、水质均衡配置的问题,从而为促进城市水资源的有效利用、推进产业结构调整提供决策依据。

1 二元水循环理论

由于人类活动的影响,实际存在的水循环包括自然系统水循环与社会系统水循环两部分(图1),其中社会系统水循环包括取水、供水、用水、耗水、中水回用、排水(回归水)等环节,水资源主要用于生产、生活及河道外生态补水等方面;自然系统水循环则主要指地下水与地表水在流域上、下游之间的运动(含降雨、蒸发、下渗等过程),体现为河道取水口处的入口水资源与排水口处的出口水资源,主要用于发电及河道内生态用水等方面;两者之间的联接点为取水、排水两个环节,它们也是社会系统水循环对自然系统水循环影响最敏感、最重要的形式。

图1 二元水循环系统

由图1可见,自然水循环与社会水循环相互联系,相互影响,构成整个水循环,它使实际存在于自然生态系统中的水是未被人类利用过的自然水与回归水的混合体。通常情况,流域上游的部分水经取水系统进入社会系统,再通过排水系统而回归到流域下游的水系统,若不经过处理和控制,这部分回归水会对水域的生态环境造成严重影响,如今的水污染问题多是因此而起。因此,在考虑水资源对社会系统的支持力时,必须要考虑水生态环境对污染物质的净化能力,也就是说,取水时必须考虑排水的生态影响。

二元水循环理论下的水资源优化配置强调对河道内外各种用水情况的整体分析,是对水资源主体及用水客体之间协调性的调配。对社会系统的水资源进行合理配置(即面向用户的水资源配置),要求在满足供水条件下,使污、废水排放量最小,并不超过河道内生态用水的环境承载能力。

2 数学模型及求解方法

根据二元水循环系统图构建城市水资源优化配置模型,以取水口处的可供水资源量为总量约束,排水口处的污径比为质量约束,对社会生产、生活及生态用水进行调配,以协调自然与社会水系统之间的均衡发展。

2.1 目标函数

a. 经济效益最大化:

maxf1=r1x1+r2x2+r3x3

(1)

式中:x1、x2、x3分别为农业用水量、工业用水量、生活用水量,万m3;r1、r2、r3分别为农业用水效益系数、工业用水效益系数、生活用水效益系数,元/m3。

b. 社会效益最大化:用人均生活用水量表示社会效益,则有

maxf2=x3/pp

(2)

式中:pp为总人口数,万人。

c. 环境负效益最小化:用工业及生活废污水的总排放量表示,要求其越小越好

minf3=d2(1-u2)x2+d3(1-u3)x3

(3)

式中:d2为工业排污系数;u2为工业用水重复利用率;d3为生活用水排污系数;u3为再生水利用系数。

d. 生态效益最大化:以河道外生态补水最大化为目标

maxf4=x4

(4)

式中:x4为河道外生态补水量,万m3。

2.2 约束条件

a. 供水总量约束:

x1+x2+x3+x4≤w

(5)

式中:w为区域可供水总量,万m3。

b. 最大最小约束:

y11≥r1x1≥y12

y21≥r2x2≥y22

x3/pp≥y32

x4≥y42

(6)

式中:y11、y12分别为农业产值的最大值、最小值,万元;y21、y22分别为工业产值的最大、最小值,万元;y32为人均供水量的最小值,m3/人；y42为最小生态补水量,万m3。

c. 污径比约束:

(7)

式中:Q为河道内生态用水量,万m3;bw为污径比。

d. 非负约束条件:

x1,x2,x3,x4≥0

(8)

2.3 求解方法

对于多目标问题,首先将各目标函数归一化,以消除不同量纲间的影响。利用下式进行:

(9)

然后将多目标问题转化为以下单目标问题:

(10)

这样,由目标函数(10)及约束条件(5)～(8)构成一个线性规划模型,利用单纯形法即可求解。

2.4 评价方法

由式(10)可知,当其中的权重取不同值时,将得到不同的可行方案(均衡解,或称非劣解),如何评价非劣解是多目标决策需要解决的一个问题。文献[9]使用“合谐度”作为一种评价方法,虽可以反映目标间的平衡性,却不能体现系统发展的程度。因为“合谐度”是基于信息熵概念的,其基本公式为

(11)

式中:p(xi)为事件xi出现的概率；n为数据个数。当p(xi)=0.367 8时,函数-p(xi)log2p(xi)可达到最大值,如图2中的虚线所示。可见,信息熵虽然能够反映变量间的平衡性,却不能反映系统本身的发展。熵的本质是系统无序度的一种度量,根据热力学第二原理,当没有外力作用时,系统熵总是增加的，也就是说,孤立系统熵应该是一个单调递增函数。于是对式(11)进行改进:

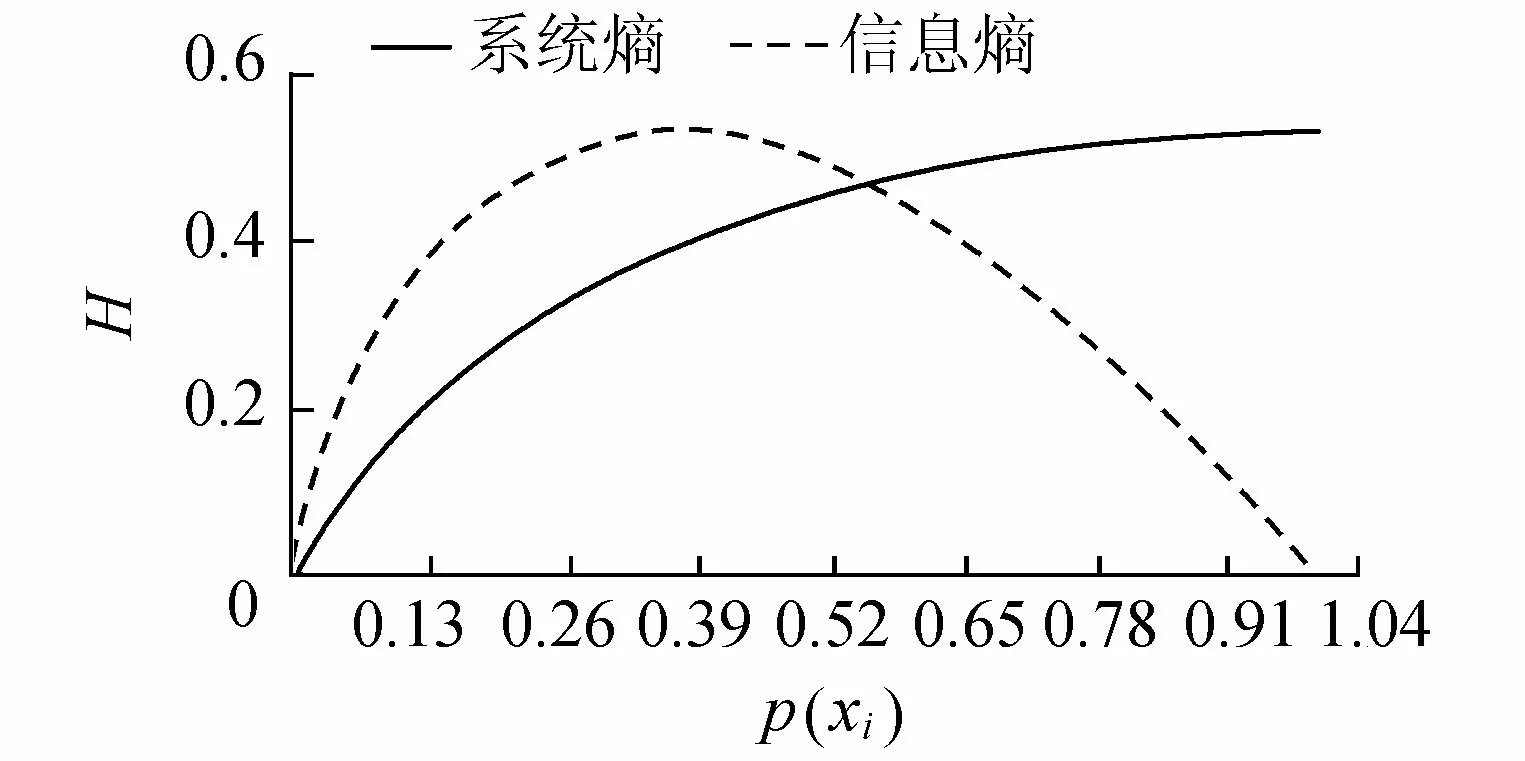
图2 系统熵与信息熵的比较

这样,H即为一个单调上升的函数,如图2中实线所示,称之为“系统熵”,方案的系统熵越小越好。当使用式(12)来评价方案优劣时,还需要确定概率p(xi)的值:

(13)

式中:xi,max、xi,min分别为xi序列的最大值、最小值;ε是为了避免p(xi)为零而附加的一个非常小的正数。

3 实 例 应 用

以昆明市2008年的水资源优化配置为例。根据《云南省统计年鉴》及《云南省水资源公报》中的有关数据,可获得以下相关参数:农业效益系数、工业效益系数、第三产业效益系数、总人口数、工业排污系数、工业用水重复利用率、生活用水排污系数、再生水重复利用率、用水量、地表径流量、工农业产值。由此利用式(1)～(8)建立数学模型如下:

这里需要对约束条件中的参数进行说明:①工、农业产值的最小值取上一年的产值(表示产值不下降),最大值使其比上一年增加15%;②根据昆明市生活用水的多年平均值,设人均用水量最小值为45 m3；③根据河道外生态补水的多年平均值,设生态补水量最小值为20 000万m3；④地表水水质一般要达到Ⅲ类水质标准才能满足水体的生态功能,而回归水执行的排放标准与其存在差距,因此污径比bw必须低于某类污染物规定的地表水水质标准与排放标准的比值Caeo,即bw≤Caeo。鉴于我国大部分地区以COD作为水环境的主要指标,这里以化学需氧量COD为评价指标,假定废污水中COD的质量浓度为100 mg/L,对于Ⅲ类地表水水体(质量浓度限值为20 mg/L),Caeo=20/100=1/5。因而取bw=0.2[13]。在实际应用中,这些参数都可以根据城市发展的规划及具体条件进行调整。

利用式(10)将多目标转化为单目标函数后,取不同的权重值,可得不同的优化方案,并利用式(11)进行系统熵评价,2008年(保证率P=45%)的计算结果列于表1中,其中方案1～5对应的权重值分别为(1,0,0,0)、(0,1,0,0)、(0,0,1,0)、(0,0,0,1)和(0.25,0.25,0.25,0.25)。

按以上方法分析2009、2010年的数据,所得优化分配列于表2、表3中。为了进行对比,表中还列出了实际的用水分配方案。由表1～表3可知：

表1 2008年(P=45%)最优配置方案评价

注：带*的数值为不同年的最小熵,下同。

表2 2009年(P=95%)最优配置方案评价

表3 2010年(P=69%)最优配置方案评价

a. 当以经济、社会为主要发展目标时,熵值较大,而以环境、生态为主要目标时,熵值较小。这里虽然方案1、2,方案4、5的优化结果一样,但都不具有普遍性,即当系统结构状态发生改变时(各参数发生变化),结果可能不同。实际用水方案的熵值界于各优化方案之间,说明实际配置中考虑了权重在各目标之间的分配。

b. 当以经济、社会为发展目标时(方案1、2),河道外生态补水满足最低要求,工、农业用水满足最低生产要求,生活用水达到最大值,但熵值也最大。因此单纯以降低工农业用水,增加生活用水(含第三产业用水)而实现可持续发展的方案并不可取,因为生活污水会产生较大的环境负效益。

c. 当环境效益权重最大时(方案3),工业、生活用水满足最低要求,农业与河道外生态补水可取到较大值。该方案值得商榷,因为在模型中未考虑农业用水可能产生的面源污染。一方面,由于农作物的生长、土壤的吸收及流域的稀释作用,很难获得因灌溉而产生的农业污染数据;另一方面,即使不分配农业用水,农业污染物质也会因降雨等气候条件而进入河流中,因此农业用水与农业污染之间没有必然联系,而控制化肥、农药等污染物质的使用才是降低农业面源污染的根本途径。因此该方案仍具有一定意义。

d. 当重视生态效益,或认为各目标权重相同时(方案4、5),工、农业及生活用水均为最小值,河道外生态补水达到最大,此时系统熵值最小。因此若要取得较低熵值,河道外生态补水应该越大越好;在水资源紧缺情况下,工、农业及生活用水只能满足最低要求。由于昆明是一个相对缺水的城市,水资源承载力处于中等偏下水平[14],为了缓解昆明市用水的紧张状态,先后进行了掌鸠河引水、清水海引水、牛栏江引水等一系列跨流域调水工程,但在进行水资源配置时,实际上还应该制定适宜的工、农业及城市发展规划,提高各行业的用水效益(降低万元产值耗水量),降低其排污系数(特别是第三产业及生活用水),实现内涵式发展,这才是实现水资源可持续利用的基本途径。

4 结 语

利用二元水循环的特点,在城市用水规划的层面上建立了水资源优化配置模型,并构建了基于系统熵的分配方案评价方法。通过在昆明市水资源配置中的应用,说明城市水资源配置应该兼顾生产、生活、环境及生态等多方效益,而当生态效益权重较大时(此时河道外生态补水达到最大值)，系统熵值较小,这将有利于城市水资源系统的长期健康发展,因此城市发展规划应该以充分考虑生态效益为前提。实例应用也表明该模型具有简洁实用,易于实现的特点,并能够反映城市整体用水的合理性及发展方向,从而为城市水资源的整体规划及结构调整提供了依据。但由于模型中没有涉及用水系统的细化特征,如取水口位置、输水成本等,因此仅适用于流域(或区域)内大尺度的水资源规划问题。