污染物对流-扩散逆过程源项反演的伴随方法
2019-03-26张文俊任华堂夏建新
胡 煜,张文俊,任华堂,夏建新
(中央民族大学环境科学系,北京 100081)
随着工业化进程的不断加快,近年来我国进入了环境高风险时期,环境污染事件以其突发性和不确定性成为环境保护的重大威胁。在水环境事故应急处理过程中,截断污染源、评估污染事故的环境影响以及污染事故的责任认定是核心内容[1],而这三者都需要根据监测数据确定污染源泄漏的位置和所泄漏的污染负荷量[2]。因此,基于污染事故发生中的监测数据进行反演确定初始时刻污染源的分布特性具有重大意义。
利用不同时刻、不同位置的监测数据确定污染源相当于求解对流-扩散方程的逆过程,该问题在一般意义上是不适定的,且极易导致数值计算发散[3]。虽然相关研究人员对正问题进行了大量研究并取得一定进展,但目前针对逆过程的研究相对较少。通常需要对源项做出必要的先验假设才能使反问题的求解具有一定的可行性。如,Ling等[4]从数学理论的角度证明了二维热传导方程在不考虑测量误差条件下未知源项位置具有唯一性,并且在基于未知源函数是若干已知源函数之和的先验假设下证明了3个测量点数据对于确定未知源函数的必要性并进行了数值验证;王泽文等[5]在对污染源及测量点的先验假设下,采用截断奇异值分解正则化方法求解离散的病态方程组,确定非零边界条件下解的唯一性,并进一步获得源项识别的局部稳定结果;而Bruckner等[6]针对波动方程的初边值问题,在监测指标向量处于有限范数的必要条件下,证明了点源识别的唯一性和稳定性。
对于反问题的求解主要有3类方法:①概率统计方法,如朱嵩等[7]基于贝叶斯推理建立了水动力-水质耦合数学模型的点源强度与位置的联合识别方法,通过马尔科夫链蒙特卡罗后验抽样获得了污染源位置和强度的后验概率分布和估计量。②遗传算法或人工神经网络方法,如闵涛等[8]应用遗传算法将源项反问题和参数反问题转化为优化问题,研究一维对流-扩散方程源项识别反问题,辛小康等[9]将遗传算法与数学分析相结合建立了水污染事故污染源识别模型。这两类方法均存在物理意义不够明确,且所需样本量比较大的问题。③伴随方法,该方法源于气象和海洋预报领域的数据同化研究[10],Bennet等[11]最早将其应用于物理海洋学领域,Tziperman等[12]相继利用该方法反演水位和海洋初始状态,国内学者马继瑞等[13]利用伴随方法反演了水位的初始场。
近年来,伴随方法逐步被引入到环境领域解决污染源反演问题,但是多数相关研究集中于边界初值或相关参数的反演,对于浓度场反演甚少涉及。如谷艺等[14]利用伴随方法根据水位观测资料反演渤海二维非线性潮汐模型的底摩擦系数;Akcelik等[15]采用Tikhonov正则化和总变差正则化[16]的方法求解了对流-扩散输运系统的边界初值反演问题;吴自库等[17]在利用伴随同化方法求解一维对流-扩散方程逆过程反问题中,从物理上对代价函数增加约束以克服不适定性与计算不稳定性,实现了污染源初始条件的反演。在实际环境污染事故中,污染物随时间在空间场中迅速迁移扩散,空间位置的不确定性极大地增加了污染源识别的难度[18]。采用伴随方法实现空间场中任意位置的污染物浓度分布时间序列反演,从而获取污染源的污染特性信息对于对流-扩散方程反问题研究具有重要意义。
本文基于伴随方法,将对流-扩散方程逆过程污染源反演转化为模型初始场最优化问题,建立目标泛函,差分求解原方程与伴随方程,确定目标泛函的下降梯度,迭代求解使得泛函达极小值,实现了污染物迁移转化逆过程反问题的求解。
1 对流-扩散方程逆过程源项反演的伴随方法
1.1 对流-扩散方程反向求解过程
污染源反演的实质是确定一个最可能的污染物初始空间分布,从而得到污染源的时空特性信息。基于此,首先建立目标泛函J:

(1)
式中:C为污染物质量浓度的计算值;Cobs为污染物质量浓度的观测值;W为权重函数,在观测点有监测资料时,其值取1,反之则取0。
污染物的迁移变化受对流-扩散方程的约束,满足该约束条件的拉格朗日函数为


(2)
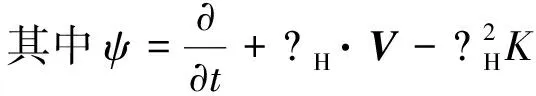
式中:λ为拉格朗日乘子;H为哈密顿算符;V为流速;K为纵向离散系数;f为污染物的源(汇)项。
当泛函L在约束条件下取得极值时,即被积函数F取得极值时,目标函数J最小。目标泛函极值条件如下:
(3)
2W(C-Cobs)+ψ*(λ)=0
(4)
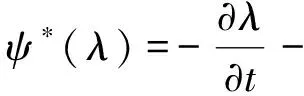
(5)
式中:ψ*(λ)为ψ(C)的伴随函数。
将式(5)代入式(4)中,得到关于污染物质量浓度C的伴随方程:
(6)
关于时间反向积分上式,得到初始时刻λi,0的全场分布,用于推算污染源相关特性。这即为反向时间积分求解对流-扩散方程的途径。
根据式(2),可以得到目标泛函相对污染物初始浓度分布C0的梯度:
∭Ω-ψ*(λ)0dΩ
(7)
其中,下标“0”表示t=T初始时刻。将式(7)写成离散形式后,得到J的增量为
(8)
式中:T*表示时间反向,即T*=T-t。
将根据式(6)得到的初始时刻λi,0的全场分布带入式(8),即可优化污染物浓度分布初始场:
(9)
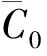
1.2 数值求解方法和计算过程
在一维条件下,对以上方程进行差分求解。对流-扩散方程、伴随方程以及式(8)的离散差分格式为
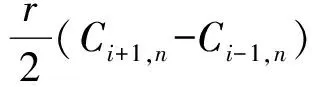
(10)
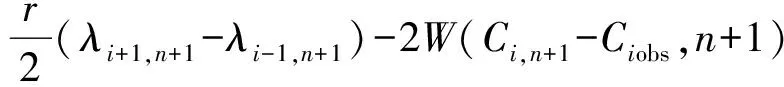
(11)
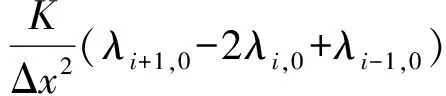
(12)
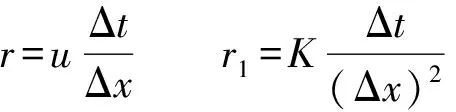
式中:u为污染物迁移速度;K为扩散系数;Ciobs,n+1为n+1时刻固定空间网格点i所监测到的污染物质量浓度值;Δt及Δx分别为时间步长和空间步长。
求解中,首先依据监测资料给定初始场的猜测值。一般而言,猜测值仅影响迭代次数,不影响计算结果,猜测值愈接近真值,所需迭代次数越少。基于猜测的污染物初始场正向积分式(10),得到污染物浓度分布空间场,并由该浓度空间分布场计算目标泛函,若泛函值小于设定误差ε,则该初始场猜测值可视为初始场实际值,否则,通过时间反向积分式(11),计算得到初始值λi,0;并进一步利用式(12)计算目标泛函的下降梯度,将其代入式(9)对污染物浓度初始场进行优化,得到浓度初始场新的猜测值,利用优化后初始场再次计算目标泛函,直至目标泛函满足误差要求,停止计算确定污染物浓度初始场。具体流程如图1所示。
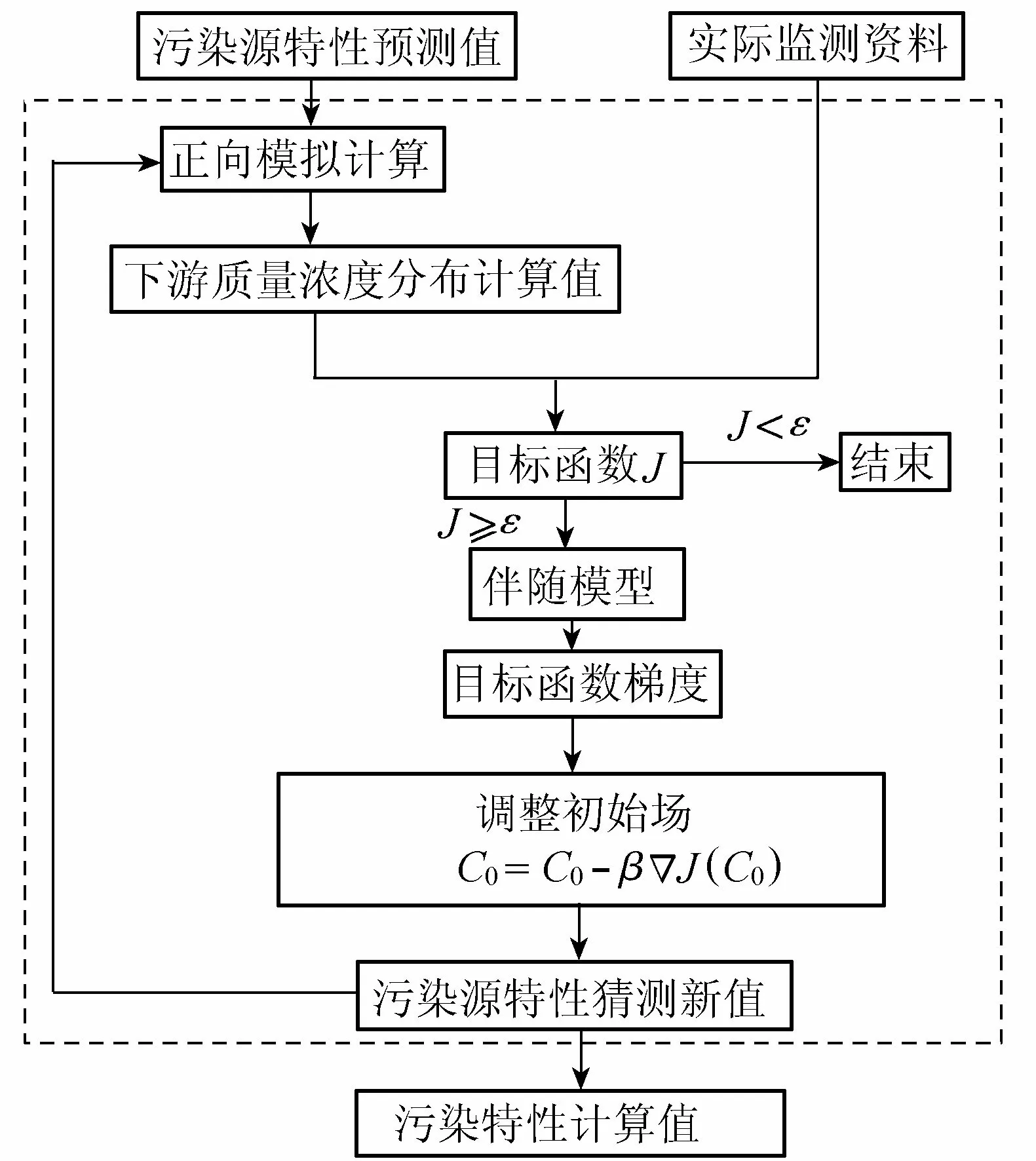
图1 污染源反演计算流程
2 数值试验与结果分析
2.1 计算工况与参数设置
为验证该方法的适用性,设计两种不同类型工况进行数值试验。工况1与工况2针对污染事故发生后根据污染物影响范围内的浓度空间分布资料,反演之前某时刻污染源的浓度空间分布;工况3根据固定监测站的污染物浓度时间序列值,反演上游某位置排放的污染物时间序列。3种工况计算的污染源均为瞬时点源形成的浓度分布,污染物为保守物质且假定在河道中瞬间充分混合,污染物在水体中表现为对流和扩散两种物理过程。
假设河道为一维,3种工况参数设置如下:污染物迁移速度均为u=1.0 m/s,扩散系数均为300 m2/s,空间步长均为500 m。为保证数值计算稳定性,工况1与工况2条件下计算所采用的时间步长为1 s,工况3条件下所采用的时间步长为2 s。
工况1已知污染源为单源且污染物质量浓度分布满足:
(13)
据此反演6.0×104s之前污染物的空间分布情况,该问题的解析解为
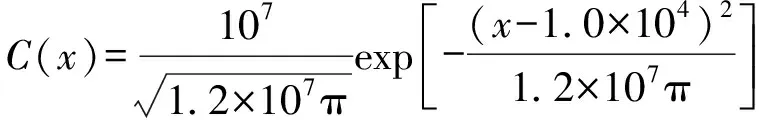
(14)
工况2已知双源形成的质量浓度空间分布为
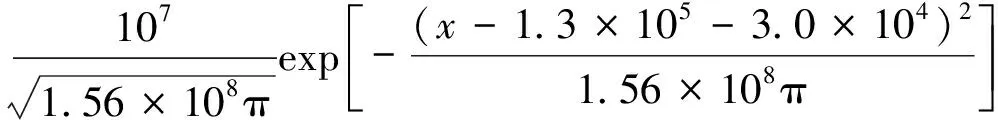
(15)
据此反演9.0×104s之前污染物的空间分布情况,该问题的解析解为
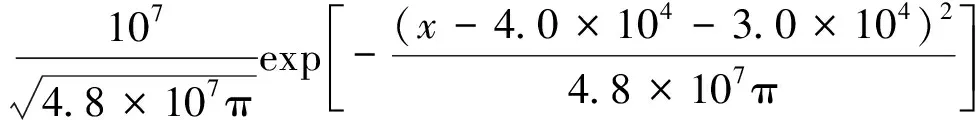
(16)
工况3给定下游固定监测站点的质量浓度分布时间序列监测值:
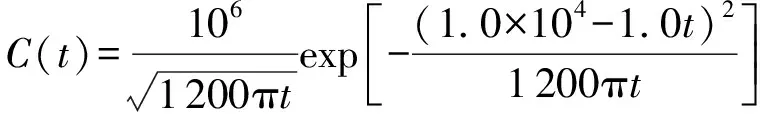
(17)
反演污染事故对于该站点上游相对距离为7.5 km的位置上游固定监测站点的污染物质量浓度分布时间序列。该时间序列的解析解如下式:
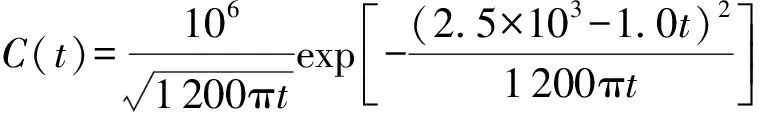
(18)
2.2 计算结果与误差分析
根据3种工况的数值实验结果进行分析,探究伴随方法对于污染源特性反演的有效性。为检验本文源项反演方法的精度,采用平均相对误差M进行衡量,定义如下:
%
(19)
式中:XP为计算值;XR为监测值。平均相对误差反映了计算值与监测值之间的偏离情况,其值越接近0,说明计算值与监测值越接近,计算准确性越高。表1列出了3种工况下目标函数的变化与满足误差要求下的迭代步数以及上游污染物浓度分布计算值与解析解、下游污染物质量浓度分布计算值与监测值之间的平均相对误差。

表1 不同工况条件下的平均相对误差
2.2.1 污染源质量浓度空间分布初始场反演
工况1条件下,上游污染源质量浓度空间分布初始场反演结果(图2)与解析解十分接近,污染负荷计算值为20 010.375 kg/m3,解析解为19 976 kg/m3,相对误差为0.2%。并且反演得到的初始场形成污染物浓度空间分布与监测值相差甚小,平均相对误差在5%之内。该结果说明本文的伴随方法在单污染源释放条件下质量浓度空间分布初始场反演中具有较好的可靠性与精确性。
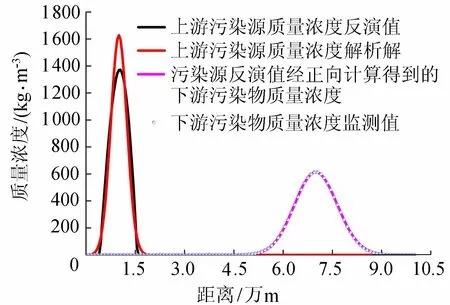
图2 工况1污染源质量浓度空间分布反演
从图3可知,工况2条件下,污染源质量浓度空间分布初始场与解析解具有较好的一致性,初始场污染负荷计算值为39 910.44 kg/m3,解析解为39 928 kg/m3,相对误差为-0.04%。同时反演得到的初始场形成污染物质量浓度空间分布与监测值相差甚小,平均相对误差仅为1.12%,显示了伴随方法在双污染源释放条件下质量浓度空间分布初始场反演的精确性。需要指出的是,当存在多个污染源时且反演时段过长可能会导致污染源混淆,此时需要结合其他资料确定污染源的数量。
在计算量方面,工况1和工况2均较小。计算过程中,目标泛函下降十分迅速,仅需迭代一百余步,即可满足精度要求,显示出伴随方法的高效性和在反演污染源质量浓度空间分布初始场时效性上的独特优势。需要指出的是,当所需反演的污染源空间质量浓度梯度过大时,容易出现解的不适定现象,计算值和真值之间会出现差异,这是由于现有的对流-扩散微分方程对浓度函数所做的光滑性假定导致,而非伴随方法本身的错误。
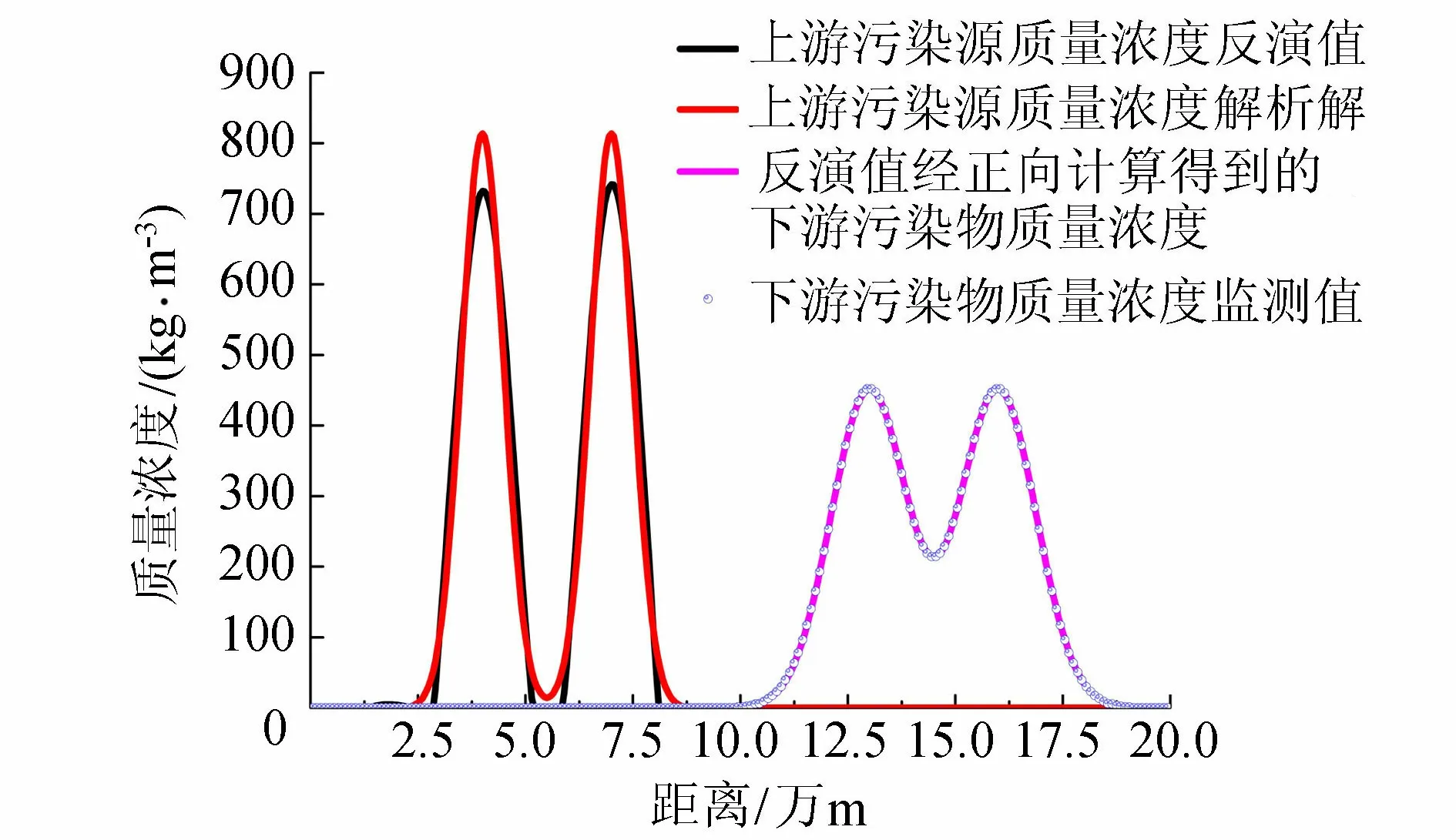
图3 工况2污染源质量浓度空间分布反演
2.2.2 污染物质量浓度分布时间序列反演
工况3条件下,上游站点污染物质量浓度分布时间序列反演值与解析解具有较好一致性(图4),平均相对误差最大不超过15%。根据反演值得到的下游染物浓度分布时间序列与监测值基本一致,进一步说明该方法的可靠性。
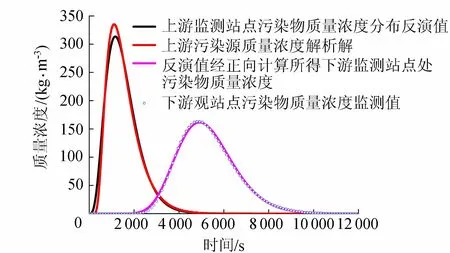
图4 工况3上游固定位置污染物质量浓度分布时间序列反演
3 结 论
a. 以污染物质量浓度监测值与计算值之间的误差的平方在时间、空间上的积分作为目标泛函,通过构建拉格朗日函数,进一步将条件约束下的泛函极值问题转化为无约束极值问题,通过求解泛函极值将污染源反演问题转化为优化问题,建立了污染源初始场的反演优化方法。
b. 应用伴随函数构建伴随方程,通过反向时间积分伴随方程并对其进行差分离散求解,避免了对污染物浓度方程直接反向积分导致的计算发散,实现了对流-扩散方程逆过程的数值求解,为反问题的求解提供了新的思路与方法。
c. 基于伴随方法,利用下游监测站点污染物浓度信息对污染源的空间初始场以及上游监测站点的浓度时间序列进行反演,能够反映污染物对流-扩散逆过程的物理机制,且在迭代计算过程中误差逐渐减小,使得反演所得污染源特性与真解十分接近,平均相对误差最大不超过15%,满足工程应用的精度要求。
