旱区植被生态需水量间接法计算参数的研究

姜田亮， 张恒嘉， 马国军， 石媛媛， 王雅云

(甘肃农业大学 水利水电工程学院， 甘肃 兰州 730070)

1 研究背景

植被恢复是退化绿洲生态系统重建的关键，对于水资源供需矛盾突出，生态环境相对脆弱的干旱地区，植被生态需水量的准确计算对于指导该区域植被生态恢复与生态建设具有重要意义[1]。目前植被生态需水量计算的方法主要有直接计算法、间接计算法、水量平衡方程法以及基于遥感技术的计算方法[2]。对地下水依赖较强的干旱地区，天然植被的生态需水量可以通过潜水蒸发来估算，即间接计算法[3-5]，计算公式为：

(1)

式中:W为天然植被生态需水量，m3；Ei为第i种植被的潜水蒸发强度，mm；Ki是第i种植被影响系数；Si为第i种植被所占面积，hm2。对上述参数进行合理计算是准确量化天然植被生态需水量的关键。

潜水蒸发强度E的大小决定着影响植物生长的土壤水分状况，土壤稳定蒸发时，地表蒸发强度与土壤含水量都保持稳定，三者在数值上相等。目前主要有两种计算方法：一种是根据降雨量、温度、辐射量等气象因素建立模型，如Penman-Monteith模型、Hargreaves模型等[6]，但这类模型的计算需要长期观测和积累大量气象数据，很难应用于部分工作基础较差(难以通过试验获取所需数据)且模型参数获取困难的干旱地区；另一种是建立潜水蒸发量与埋深的关系模型，常见的关系模型大体可分为3类：第1类是潜水蒸发系数与潜水埋深呈单一的相关关系，如叶水庭指数型公式[7]，由于忽视了E与蒸发能力相关的规律，故有一定的局限性。第2类公式对此进行了改进，同时考虑了E与埋深及蒸发能力的关系，如沈立昌公式[8]。第3类是潜水蒸发系数与土壤输水特性及土表蒸发具有相互关系，如雷志栋公式[9]。已有研究表明[10]，后两类公式拟合埋深大于1 m的实测资料较好。由于3类计算公式具有不同的适用条件，本文基于MATLAB软件利用去极值法和0.618法对7个常用公式所得结果进行优选，并提出一种无实测数据情况下的潜水蒸发量估算方法。

植被系数K反映了一定区域内植被对潜水蒸发量的影响，不同植被适宜生存的地下水埋深不同，利用植被地段的潜水蒸发量除以无植被地段的潜水蒸发量求得[11]。目前旱区植被系数选取，主要参照河西走廊玉门镇有关的试验结果[12]，即查表法。为克服查表法信息局限的缺点，本文基于已有试验数据建立了潜水埋深与植被系数间的关系函数，为植被系数K的选取提供更为科学有效的方法。

植被覆盖面积S是一个地区生态环境的综合反映，现阶段，植被覆盖面积一般通过遥感影像人工解译土地利用覆盖图，在此基础上运用ARCGIS9.0软件统计出各种天然植被的覆盖情况[13]。研究植被面积的变化趋势的常用方法有时间序列法、灰色模型法、生长曲线法、生产函数法、回归分析法和马尔科夫模型等[14]，其中灰色模型GM(1,1)不需要大量样本就能得到较为准确的预测结果，可应用于干旱地区植被面积的预测分析。

通过对公式中参数值的优选及算法改进，有助于植被生态需水量的准确量化和间接计算法的推广，为旱区水资源的分配及生态恢复政策的制定提供合理依据。

2 试验地点及数据来源

2.1 民勤县概况

民勤绿洲位于38°03′～39°28′N、101°49′～104°12′E，沿石羊河两岸呈西南-东北向带状分布，西、北、东三面被巴丹吉林沙漠和腾格里沙漠包围。气候干燥，降水稀少，蒸发强烈，温差较大，属于典型的干旱地区，多年平均蒸发量2 644 mm[15]。历史记载中民勤水草丰盛，草甸及沼泽植被是过去绿洲主要的原生植被[16]。现如今地下水的严重超采致使地下水埋深急剧加大，土壤盐渍化、沙化，水质恶化日益严峻，进而导致植被覆盖率降低,生态环境遭到严重破坏，给经济发展和区域内人民的生活带来了严重的威胁[17-18]。因此，民勤地区植被生态需水量准确计算对指导该地区水资源的优化配置与生态建设具有重要的意义。

2.2 数据来源

民勤地区各类植被面积数据以《民勤县国民经济和社会发展统计资料汇编》[19]为准；对照组使用张奎俊[16]对石羊河流域下游进行研究所得潜水埋深-蒸发埋深数据；阿维里昂诺夫参数的选取依据中科院寒区旱区研究所和甘肃省水文二队在典型干旱区玉门、张掖试验所标定的值[20-21]；各植被最适地下水埋深数据以栗晓玲[22]和杨秀英等[23]的研究为依据。

3 研究方法

3.1 潜水蒸发量E的优选

由于现有潜水蒸发模型适用条件不同，若利用常规方法对潜水蒸发量计算，则对不同埋深下的潜水蒸发量反映不够理想。因此，利用MATLAB将各类公式(表1中公式1～7)编入同一个程序，分别对不同埋深的潜水蒸发点进行拟合，排除不满足相关度的模型公式后，结合去极值法和0.618法进行结果优选，编程思路如下：

由于民勤县极限地下水位埋深hmax为4.5m[18]，因此h以[1,4.5]为区间、0.01为步长增长，代入各公式得到350组不同的潜水蒸发量，构成矩阵E：

去掉每行的最大值、最小值得到新的矩阵E′：

用下式求得优化结果E优化:

(2)

(i=1,2,…,350)

表1 潜水蒸发公式

注：a,b,c为经验参数，即拟合系数；E0为大气蒸发量,mm/d；h为地下水埋深,m。

针对部分研究地区试验条件有限，缺乏实测潜水蒸发量-埋深数据的现状，可以根据研究区的土壤和气候特点，使用相似地区阿维里昂诺夫经验参数模拟出数据点进行计算。阿维里昂诺夫模型形式简单(公式8)，易于推广，现已被广泛应用于实际生产，积累了大量的研究资料。选取3组阿维里昂诺夫经验参数，以3组不同的潜水埋深(1、2、3、4 m);(1.35、2.65、3.35、4.35 m);(1.75、2.25、3.75、3.85 m)生成模拟蒸发点进行拟合。

3.2 植被影响系数K的计算

K值的常规解法是查表法[22-23]，如表2所示。但当潜水埋深取值不在表中时，K只能通过专业人员估值得到，降低了结果的准确度。利用MATLAB中的二阶Gaussian函数对数据进行准确拟合，结果如公式(3)和图1。

(3)

式中:h为潜水埋深,m。经检验，R为0.9957，拟合度较高。

图1 Ki值拟合曲线

表2 干旱区潜水埋深与植被影响系数表

3.3 植被面积S的研究预测

利用灰度模型GM(1,1)分别对乔木林、灌木林、疏林地、高盖度草地、中盖度草地2005-2014年的面积数据进行率定，通过后验差检验，得到2015年各植被面积，与记载资料[19]进行对比验证，进而对2020年植被面积进行预测。灰度模型具体思路如下[29]：

(1)各植被面积原始序列数据为x(0)(k)={x(0)(1),x(0)(2),…,x(0)(n)}，并对其作累加处理得：x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}，k=1,2,…,n。

(2)灰度模型GM(1,1)的建立。即：

(4)

式中:μ为内生控制灰数;α为发展灰数。

(3)向量Y和矩阵B的构建：

(5)

Y=[x(0)(2),x(0)(3),…,x(0)(n)]T

(6)

(4)利用最小二乘法估计模型参数可得：

a=BT(BTB)-1Y

(7)

(5)预测模型求解：

(8)

k=0，1，2，…，n

(6)利用累减还原法得到灰色预测模型：

(9)

(7)后验差法计算残差，得：

(10)

k=1,2,…,n

(11)

(12)

后验差比为:

C=S2/S1

(13)

精度检验等级如表3所示。

表3 精度检验等级参照表

4 结果分析

4.1 潜水蒸发量

在充分考虑不同植被盖度的蒸腾量、不同水质以及地下水埋深与植被蒸腾量的相关关系的基础上，对表4中阿维里昂诺夫初始参数生成的模拟点进行拟合，结果如图2～5。各公式拟合度均大于R0.05，线性关系合理，与3种经典公式相比，优选曲线拟合程度更好。与张奎俊[16]在民勤所做潜水蒸发试验结果进行对比，相关系数R分别为0.918，0.917，0.907，0.926，P值分别为0.912，0.849，0.900，0.911，0.934，其中优化结果的相关系数最大，且无差异的显著性水平最高，如表5所列，说明了优化的合理性。

表4 阿维里昂诺夫初始参数

图2 沈立昌公式拟合结果 图3 叶水庭公式拟合结果

图4 雷志栋公式拟合结果 图5 优选结果

表5 各公式拟合结果与张奎俊模拟点相关性分析及差异性检验

4.2 植被系数

据粟晓玲[22]和杨秀英等[23]的研究，民勤地区乔木林的最适地下水埋深为1～4.5 m，灌木林3～4 m，疏林地3.5～4.5 m，高覆盖度草3～4.5 m，中覆盖度草4～4.5 m。选取中间值作为计算埋深代入公式(2)，得到各类植被影响系数及潜水蒸发量，结果如表6所列。

表6 各类植被不同地下水埋深植被影响系数及潜水蒸发量

4.3 植被面积

利用民勤县2005年至2014年的数据对模型进行率定，依据公式(4)和(7)计算得出 ，代入式(8)则分别得到乔木林、灌木林、疏林地、高覆盖度草及中覆盖度草的面积累计预测公式，得到5个单一灰色GM(1,1)模型，结果皆通过后验差法进行检验。基于Matlab编程并代入面积数据运行，结果如表7。

在此基础上计算，到2015年，乔木林、灌木林、疏林地面积分别为1 475、7 181、13 025 hm2，高覆盖度草地和中覆盖度草地面积分别为1 571、6 873 hm2。《民勤县2015年国民经济和社会发展统计资料汇编》统计，乔木林、灌木林、疏林地面积分别为1 498、7 943、12 901 hm2，高覆盖度草地、中覆盖度草地面积分别为1 600、6 954 hm2。两组数据p值为0.9611，无差异。2015年结果如图6～10所示。代入公式 (1)，得到2015年民勤县生态需水量为3 726.8×104m3，其中乔木林需水量为299.0×104m3，灌木林1 208.9×104m3，疏林地需水量为1 310.2×104m3，高覆盖度草为217.3×104m3，中覆盖度草地为691.4×104m3。

表7 各植被类型面积计算公式及后验差检验

注：k=2～10，代表2006-2014年的时间序列，x(0)(1)为2005年的植被面积。

图6 乔木林面积增长趋势 图7 灌木林面积增长趋势 图8 疏林地面积增长趋势

因此可以预测，到2020年，民勤县乔木林面积将达到1 623 hm2，灌木林7 899 hm2,疏林地14 328 hm2,高覆盖度草1 728 hm2,中覆盖度草7 141 hm2。届时民勤县天然植被生态需水量为4 060.8×104m3，其中乔木林329.0×104m3，灌木林地1 329.8×104m3，疏林地1 441.3×104m3，高覆盖度草地239.0×104m3，中覆盖度草地721.7×104m3。

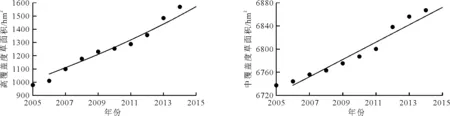
图9 高覆盖度草面积增长趋势 图10 中覆盖度草面积增长趋势

5 讨 论

本研究探求潜水蒸发量E是对众多潜水蒸发公式所得结果的优选，无具体的模型公式，所得潜水蒸发量-埋深曲线是由大量优选点组成的折线，需要借助计算软件(如MATLAB)进行编程求解。由图2～5可见，当埋深较浅时，对潜水蒸发量取值影响较大的是第一类公式；当埋深大于3.5 m，由更适宜计算该埋深条件的二、三类公式决定潜水蒸发量降低速率，因此图5中优化的潜水蒸发量-埋深曲线更具有代表性。

由图1见，植被系数K的减小速率随埋深增先逐渐变小，后趋于稳定，最后逐渐变大。已有文献[30-31]发现，不同植被影响系数的大小是一个随潜水埋深变化的函数，其值随地下水埋深的增大而减少。当地下水埋深小于2 m时，减小速率随埋深的加大逐渐变小，当埋深在2～3 m时，K值趋于稳定；当埋深大于3 m时，减小速率逐渐上升,可以用二阶Gaussian函数精确的拟合。朱艳红[32]研究表明,干旱地区地下水埋深小于2 m时，土壤含水率减小速率随埋深加大逐渐变小，当潜水埋深大于2 m时，土壤含水率趋于稳定。上述变化规律与图1中K值变化趋势一致。因此可得出，在潜水埋深小于3 m的范围内，土壤水蒸发是影响旱区植被生态需水量的主要因素，此时K值的变化速率与土壤含水率变化速率一致。当潜水埋深大于3 m时，土壤水蒸发对植被生态需水量的影响逐渐变小，而地表植被由蒸腾作用更为强烈的乔木、灌木变为蒸腾作用较弱草地，导致K值迅速变小。

Penman-Monteith模型是一种根据降雨量、温度、辐射量等气象因素建立的潜水蒸发模型，郝博等[33]利用该模型计算得出2015年民勤县总生态需水量4 118×104m3，其中乔木林278×104m3，灌木林地1 194×104m3，疏林地1 431×104m3，高覆盖度草地203×104m3，中覆盖度草地702×104m3。与本研究所得结果相比，各类植被生态需水量相关度为0.9739，大于R0.05，p值为0.962，两者无差异。总生态需水量较本研究结果偏高，究其原因是该方法计算结果中的天然林地包括除以上3种林地外的其他林地。

6 结 论

(1)通过优化植被生态需水量间接法计算公式中每个参数，更加准确的计算和预测了民勤县的天然植被生态需水量，该方法也为我国部分环境恶劣、试验条件艰苦而难以取得准确观测数据的干旱地区生态需水量的估值提供了科学的参照。其中潜水蒸发量的算法以去极值法和0.618优选法为基础，植被影响系数的核心是一元函数的拟合，植被面积的计算及预测运用灰色模型理论，整个方法所使用的理论简单有效、可操作性强，是一种容易推广的计算方法。

(2)预测得到2020年民勤县的生态需水量将达到4 060.7×104m3，即2015年至2020年以每年66.78×104m3的速度增加。为了恢复绿洲植被面积，实现民勤绿洲的社会经济可持续发展的战略，必须先满足绿洲天然植被的生态需水。地下水的持续超采是民勤绿洲生态恶化的主要原因，因此石羊河的地表径流是民勤最主要的供水源。所以，在合理规划生活、生产用水的前提下，增加进入民勤绿洲的地表水量，是解决水资源危机、缓解地下水持续超采、保证民勤绿洲安全的最重要对策，亦是不容延误的当务之急。

(3)本研究对民勤县潜水蒸发量进行估算时，由于未使用实测潜水蒸发量-埋深点，因此估算结果很大程度上取决于阿维里昂诺夫公式初始参数的选择，其中初始参数a与优化结果呈正相关，b呈负相关。为了更加准确的估算天然植被生态需水量，消除估算所得潜水蒸发量与实际值间偏差，今后应考虑观测和确定不同植被类型在不同地下水位所对应的潜水蒸发参数，准确掌握植被蒸腾与潜水位之间的关系，以提高生态需水的计算精度。