考虑蒸发锋面的包气带一维液相运动方程解析解

刘梦茹, 程大伟, 卢玉东

(1.长安大学 环境科学与工程学院, 陕西 西安 710054; 2.长安大学 旱区地下水文与生态效应教育部重点实验室, 陕西 西安 710054)

1 研究背景

包气带是大气水、地表水、地下水三者之间发生水力联系并进行水分交换的场所，同时也是地表污染物进入地下的通道。因此包气带中液相运动的研究在地下水污染管理、维持地下水采补平衡[1]等领域中有着广泛的应用。包气带中土壤湿度是控制水分交换的关键因素，其状态受季节和气候变化的影响[2]。在雨季，降雨作用在包气带中形成的液相运动为稳态入渗[3]；在旱季，土面蒸发和植物蒸腾是控制包气带中潜水位以上区域液相运动的主要因素。多数学者在推导包气带液相运动方程时仅考虑入渗情况，而由蒸发所引起的包气带液相运动在实际中大致可以分为以下两种形式[4-7]：当地下水位深度足够浅时，包气带液相运动完全受毛细作用控制，始终维持水力连续，且服从达西定律;当地下水位深度超过某一临界深度时，受到重力因素及黏滞力的影响，蒸发锋面[7]将会由地表向地下水位发展。

在推导包气带一维液相运动方程解析解过程中常用幂函数型或指数型渗透函数，诸如线性模型[8]、基于Brooks-Corey土水特征曲线建立的渗透性函数模型[9]、低饱和度下Van Genuchten 模型[10-11]、常数渗透系数模型[12]等均为幂函数型渗透性函数[3]。由于幂函数型渗透性函数在推导液相运动方程解析解时变量难以合并,导致所获得的解析解常为负压水头的隐式表达，此外，在求解的过程中这些解仅考虑入渗情况。Gardner模型为指数型渗透系数函数，可对液相运动方程进行线性化处理，易推导解析解。在稳态入渗或蒸发条件下,一维液相运动方程的解析解相比数值解简洁[13],并且易基于相应解析解建立反演模型,进行参数反演，从而具有广泛的实际应用,如通过实测数据反演估计水力参数、为更复杂的液相运动提供标准测试方案等。

本文基于指数型渗透系数模型Gardner模型求解扩散度，分别推导在稳态入渗和稳态蒸发两种情况下包气带中均质土和成层土液相运动方程的解析表达以及蒸发锋面深度表达式。分析各水力参数对一维液相运动方程的影响并通过解析解进行水力参数的反演。

2 均质土水力连续区有效饱和度剖面及蒸发锋面深度的解答

LU Ning等[14]通过给定适当的初始条件和边界条件，推导出以基质吸力为变量的液相运动方程解析解。本节在此基础上，推导出有效饱和度剖面解析解。

2.1 均质土水力连续区液相运动方程解析解

一维稳态流下包气带液相运动方程边值问题可写作如下形式：

(1)

式中：θ为含水量，m3/m3；D(θ)为扩散率；K(θ)为非饱和土渗透系数，m/s。

非饱和土的渗透系数是负压水头的函数，常被定义为：

K=KsKr

(2)

式中：Ks为饱和土渗透系数；Kr为相对渗透系数。

在非饱和土中,相对渗透系数Kr和含水量θ均为负压水头的函数[15]。Gardner模型常被用于求解析解，所描述的相对渗透系数与负压水头之间呈指数关系，即

Kr=eαgh

(3)

式中：αg为Gardner模型参数。

(4)

式中:Se为有效饱和度;θr为残余含水量;θs为饱和含水量。公式(4)即为Srivastava提出的指数型土水特征关系[16]。

将公式(4)转化为负压水头与有效饱和度的关系，则有：

(5)

将式(5)代入式(1)，则为负压型液相运动方程。文献[14]给定下边界为水头边界条件，即z=0时，负压水头为h0；上边界为流量边界条件，即z=H，比流量为q，建议了如公式(6)的解析解：

(6)

当采用负压水头h为变量时,公式(6)中μa-μw的绝对值与负压水头绝对值大小相等，将公式(4)及公式(6)化简合并得：

(7)

公式(7)即为包气带一维液相运动方程解析解，该解析解表明土层中有效饱和度剖面受比流量、下边界负压水头、孔隙分布特征和渗透性控制。

若下边界为潜水位时，则z=0,h0=0,有：

(8)

2.2 均质土蒸发锋面深度

若规定比流量q在入渗时为负，蒸发时为正，当比流量q小于临界比流量qc时，液态水饱和度剖面在整个区域内延伸。当比流量q大于临界比流量qc时，自地表以下至蒸发锋面处土孔隙内流体为气体，液态水仅存在于潜水面至蒸发锋面区间内。定义蒸发锋面处的有效饱和度为临界有效饱和度Sec。参考Hayek[3]建议采用在地表处土中水有效饱和度为零时对应的蒸发率为临界比流量，即:

z=H,Se=0

(9)

将公式(9)代入公式(8)，则有：

(10)

当q>qc时，只需要将临界有效饱和度Sec代入公式(7)即可推导得蒸发锋面深度(蒸发锋面距离地下水位的高度)为：

(11)

公式(11)表明蒸发锋面深度除受比流量、孔隙分布特征和渗透性影响外，还与临界有效饱和度Sec有关。

3 成层土水力连续区有效饱和度剖面及蒸发锋面深度的解答

均质土的分析常用于实验室研究,成层土常见于实际工程中。根据Darcy定律和质量守恒定律推导包气带中成层土液相运动方程的解析解以及相对应的蒸发锋面深度模型。

3.1 成层土水力连续区液相运动方程解析解

现讨论两种渗透性不同的土构成非饱和成层土[17]的情形，如图1所示。令土层的总厚度为L,土层1的厚度为z1,土层2的厚度为L-z1。土层1和土层2的界面位置在z=z1处，每层土为均匀线弹性均质土。根据Darcy定律和质量守恒定律，非均质界面处土层1和土层2应满足负压水头和比流量分别相等。即有：

h1z1=h2z1

(12)

q1z1=q2z1

(13)

式中:h1z1、h2z1分别为非均质界面土层1的负压水头和土层2的负压水头；q1z1、q2z1分别为非均质界面处土层1的流量和土层2的流量。

图1 成层土剖面示意图

土层1底面为地下水位，故利用式(7),可得土层1中有效饱和度剖面为：

参考译文:Konka Group has been granted“National Advanced Quality and Benefit Enterprise”and“National Customer Satisfied Enterprise”for several years．

(14)

当z=z1时，根据负压水头和有效饱和度的关系，可知：

=h2z1

(15)

故对于土层2，其有效饱和度剖面为：

(16)

3.2 成层土蒸发锋面深度

对于成层土而言，在稳态蒸发条件下，蒸发锋面深度受比流量影响较大，参考Hayek[3]的建议，本文为便于处理,取土层2顶部有效饱和度为零所对应的比流量为土层2的临界比流量qc2，即z=L,se2=0，代入公式(16)可得土层2的临界比流量应满足：

qc2=

(17)

定义蒸发锋面位于土层非均质界面处所对应的比流量为临界比流量qcl。当蒸发锋面深度zDF=z1时，即土层2在非均质界面处的有效饱和度Se2,z1为土层2的临界有效饱和度Sec2。将该条件代入公式(16)，可得非均质界面处的临界流量qcl为：

(18)

定义成层土中各土层按所计算土层顶部有效饱和度为临界饱和度计算临界比流量，则土层1的临界比流量应满足当z=z1时Se1=Sec1，代入公式(14)可得：

(19)

当qc2≤q≤qc1时，蒸发锋面在土层2内，则由公式(16)可得蒸发锋面深度为：

(20)

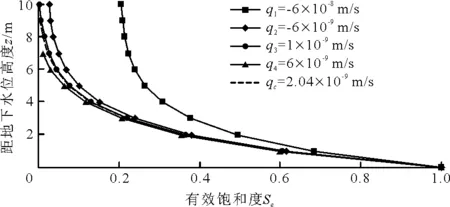
当q≥qc1时，蒸发锋面可能在土层1内时，若比流量q

(21)

此时，在土层1中0≤z≤zDF内有液态水运动，并服从达西定律。

4 水力参数反演

解析解重要的一种应用是反演水力参数。水力参数反演的难易程度取决于反演参数的个数。解析式(8)中涉及的水力参数包括Gardner模型参数αg和饱和渗透系数Ks。通过假设已知土层底面为潜水面来反演上述2个参数，比流量q、负压水头h1、z1处的有效饱和度Se1、z2处的有效饱和度Se2均为已测定值，具体反演过程如下：

将(z1,Se1),(z1,h1)代入公式(4)及公式(8)，化简可得：

(22)

将(z2,Se2)代入公式(8)求得αg的表达式如下：

(23)

将公式(22)代入公式(23)，整理可得：

(24)

公式(24)是关于αg的超越方程，需利用迭代求根法求解。

5 结果与讨论

5.1 比流量q和模型参数αg对有效饱和度剖面的影响

图2所示为厚度H=10 m土层在不同比流量q下有效饱和度剖面。主要参数依次为：αg=0.5 m-1,Ks=3×10-7m/s,qc=2.04×10-9m/s，q1=-6×10-8m/s，q2=-6×10-9m/s，q3=1×10-9m/s，q4=6×10-9m/s。根据图2可知，当比流量小于临界比流量时，地表处的有效饱和度随着比流量的增大而减小，且不同比流量下有效饱和度剖面之间的差异随距离地下水位高度的减小而减弱。当比流量大于临界比流量时，土层中存在蒸发锋面。土中饱和度剖面以下所围面积反映了土层中液态水质量分数相对大小，随着比流量的增大，土层中液态水质量分数减小。

图2 不同比流量下有效饱和度-深度关系曲线

图3为厚度H=10 m土层在不同模型参数αg下有效饱和度剖面。地下水位于土层地面以下10 m处。主要参数为：αg取值分别为0.05、0.5、1、2 m-1,q=-3×10-8m/s，Ks=3×10-5m/s,由图3可知αg对有效饱和度剖面影响较大，相同深度处的有效饱和度随αg值得增大而减小。当αg值较大(如αg=2 m-1)时，地表下部土层一定区域内的有效饱和度近似等于地表处的有效饱和度，在该区域以下有效饱和度会骤增，直至地下水位处变为1。此时液相运动主要受重力控制。当αg值较小(如αg=0.05 m-1)时，毛细作用发挥支配作用，有效饱和度趋于线性变化。

图3 不同αg下有效饱和度-深度关系曲线

5.2 成层土中有效饱和度剖面的变化特征

为分析稳态流下成层土有效饱和度随深度的变化，设定土层A和土层B的厚度均为5 m。土层A的主要参数为：αg=1 m-1，Ks=3×10-5m/s;土层B的参数为:αg=0.5 m-1，Ks=3×10-7m/s。土层A具有比土层B较高的孔隙连通状态和透水性。

5.2.1 入渗条件下成层土有效饱和度剖面 图4为稳态入渗条件下成层土内有效饱和度剖面。其中工况1为土层B在上部，土层A在下部；工况2为土层A在上部，土层B在下部。比流量q=-3×10-8m/s。

工况1情况下，上部土层B的有效饱和度小于相同深度处均质土B的有效饱和度；工况2情况下，上部土层A的有效饱和度大于相同深度处均质土A的有效饱和度。而对于下部土层，由于下边界水头与均质土下边界条件相同，无论是工况1还是工况2均与对应均质土层的有效饱和度-深度关系曲线重合。

图4表明稳态入渗下，当下部土层透水性较好时，上部土层中的液态水向下层流动，液相运动增强，其有效饱和度与均质土相比要小。反之，当下部土层透水性较差时，上部土层中的液态水向下层流动受到阻滞，液相运动减弱，其有效饱和度与均质土相比要大。

图4 入渗条件下成层土有效饱和度-深度关系曲线

5.2.2 蒸发条件下成层土有效饱和度剖面 图5为稳态蒸发条件下成层土的有效饱和度剖面。其中，工况3为土层B在上部，土层A在下部；工况4为土层A在上部，土层B在下部。比流量q=1×10-8m/s。由图5可知，在蒸发条件下工况3的上部土层B内有效饱和度大于相同深度处均质土B的有效饱和度；工况4的上部土层A的有效饱和度小于相同深度处均值土A的有效饱和度。下部土层中，由于下边界水头与均质土下边界条件相同，工况3、工况4均与对应的均质土层的有效饱和度-深度关系曲线重合。

对比上部土层的有效饱和度，可以发现在稳态蒸发下，若下部土层透水性较好，上部土层中液相运动增强会储存较多的液态水，同时蒸发锋面距地表更浅；反之，当下部土层透水性较差时，上部土层中液相运动受阻减弱，储存液态水较少，蒸发锋面距地表更深。

图5 蒸发条件下成层土有效饱和度-深度关系曲线

5.3 参数反演分析

5.3.1 参数反演模型的可靠性 假设土层底面为地下水位，给定q=-3×10-8m/s,αg=0.5 m-1，Ks=3×10-7m/s。选择两个观测点Z1=8 m,Z2=4 m,利用公式(8)获得Z1处有效饱和度精确解为0.116 5，将Z1处精确解代入公式(5)中，可得负压水头的精确解为-4.299 73；Z2处的有效饱和度精确解为0.221 8。将上述数据代入公式(24)中求得αg值为0.5 m-1,再代入公式(22)求得Ks值为3×10-7m/s。结果表明参数反演模型的正确。

6 结 论

本文利用相对渗透系数模型中的Gardner模型分别推导了均质非饱和土和成层非饱和土中一维液相运动方程解析解，获得了蒸发锋面深度的计算表达式，所得结论具体如下：

(1)包气带中均质土有效饱和度是深度的函数，受比流量、下边界负压水头、Gardner模型参数等参数控制。相同深度处的有效饱和度随着比流量和Gardner模型参数的增大而减小。

(2)对于给定比流量和土层参数的非饱和成层土中，土层内的有效饱和度剖面主要受下边界负压水头控制。在稳态入渗或稳态蒸发条件下，下部土层的有效饱和度剖面与相应均质土的有效饱和度剖面重合；上部土层的有效饱和度受下部土层透水性的影响。

(3)由于蒸发锋面的存在，包气带中均质土和成层土液相运动方程的解析解的适用范围在临界有效饱和度与饱和有效饱和度之间。

(4)测试了参数反演模型的可靠性，分析测量数据误差对参数反演结果影响。结果表明所建议的参数反演表达式是可靠的，参数反演的结果受测量误差的影响较小。