基于大涡模拟的悬板径向坡度对排沙漏斗流场特性影响数值模拟
2019-03-26王平圆吴洋锋
王平圆, 吴洋锋, 李 琳
(新疆农业大学 水利与土木工程学院, 新疆 乌鲁木齐 830000)
1 研究背景
排沙漏斗是一种二次处理泥沙的设施,它独特的特点是利用三维涡流特性进行水沙分离,同时还具有排沙耗水率低、截沙率高等的优点[1]。它主要由矩形进水洞口、柱体和锥体组成的漏斗室、溢流悬板、排沙底孔、溢流侧槽、溢流侧槽出口等结构组成。溢流悬板是排沙漏斗处理泥沙的重要构件,它的圆心角为180°,外缘长等于漏斗的半周长,宽度与漏斗的的直径成正比变化,它的存在既能够减少例如推移质泥沙在排沙漏斗进口处沉积,而且还能够使悬移质泥沙跟螺旋水体沿漏斗室内旋转一圈,到漏斗内水流速度缓慢区域沉降,然后通过漏斗底孔处排出,这样就很有利于细小泥沙的清除。除此之外,设置排沙漏斗后的漏斗室中心区域的空气漏斗的面积也会变小,排沙耗水量随之也很大程度地降低[2-10]。前人针对流场特性对排沙漏斗水沙分离性能和泥沙沉降输移特性的影响开展了大量研究,如唐毅等[11]通过物理实验、数值模拟对比分析了排沙漏斗清水流场结构,肖柏青等[12]和Chapokpur等[13]通过VOF方法计算了漏斗内水气二相流流态,邱秀云等[14]、肖柏青等[15]对排沙漏斗流场特性及排沙机理进行了研究。工程实践证明处理推移质泥沙的排沙漏斗能够对直径为0.1 mm以上泥沙的截除率达100%,处理悬沙的排沙漏斗对直径为0.05~0.1 mm的泥沙截除率可达77.5%,对于直径为0.005~0.05 mm的泥沙截除率平均可达65%,对于粒径为0.001~0.005 mm的泥沙截除率平均可达62.3%[16]。但是近些年来处理悬沙的排沙漏斗出现了由于悬板自重大、悬板上泥沙淤多及落后的运行管理造成悬板及其支撑系统失稳坍塌。例如陕西泾惠渠排沙漏斗工程、新疆喀什一级电站排沙漏斗工程都在处理悬移质泥沙的过程中都出现了悬板支撑破坏问题[16-17]。吴洋锋等[5]提出了改变溢流悬板沿径向坡度,使其沿径向漏斗中心倾斜来减少溢流悬板上的泥沙淤积,并利用粒子图像流场测速技术(PIV)研究了悬板径向坡度变化对排沙漏斗室内流场特性的影响。但受漏斗悬板和圆柱形壁面折射的影响,试验过程中仅对排沙漏斗90°和270°垂直测试面和三个水平面的三维速度场进行了量测,且排沙漏斗边壁和悬板附近区域无法量测。为了弥补试验的不足,全面了解溢流悬板径向坡度的改变后排沙漏斗内部完整的流场特性。本文采用了大涡模拟和VOF方法对改变溢流悬板径向坡度时排沙漏斗三维流场进行了数值模拟,应用吴洋锋等[5]的试验结果检验数学模型及其参数,基于数值模拟结果对悬板径向坡度改变时的排沙漏斗内部完整的流场特性进行分析。同时应用DPM(离散相模型)模型模拟了溢流悬板径向坡度不同时排沙漏斗对不同粒径泥沙的截除率,为排沙漏斗优化悬板布置提供参考。
2 湍流数学模型
湍流包含一系列大大小小的涡团,涡的尺度范围相当宽广。大涡模型(LES模型)的控制方程是对N-S方程进行过滤得到的。过滤后的控制方程为:
(1)
(2)

(3)
式中:usgs为亚网格湍流黏性系数;Sij为求解尺度下的应变率张量,定义为:
(4)
利用Smagorinsky-Lilly模型来计算亚网格湍流黏性系数:
(5)
Ls=min(KD,CSV1/3)
(6)
式中:LS为亚网格尺度的混合长度;K为卡门常数,大小取0.42;D为到最近壁面的距离;V为计算控制体体积;CS为Smagorinsky常数,它是对亚网格湍流黏性系数进行描述时引出的一个参数对大小取0.1。
VOF模型(Volume of Fluid Model)[18]是Hirt(1981)和Nichols(1976)在MAC方法基础上提出的适合于两种或多种互不穿透流体间界面追踪的计算方法。当控制体内气相流体的体积分数α=1,即该控制体内无水,被气相充满;当α=0时,表明控制体内被水充满,无气相;当0<α<1时,控制体同时被水相和气相充满。气相体积分数α的控制微分方程为:
(7)
ρ=αρα+(1-α)ρw
(8)
式中:α表示气相的体积分数,ρα为气相密度;ρw为水相密度。
离散相模型(DPM)在收敛的连续相流场中对离散相使用拉格朗日法求出颗粒的轨道。DPM模型的颗粒轨迹微分方程为:
(9)
式中:下标p为离散相悬移质颗粒;t为离散时间;τp为颗粒松弛时间;U为流体的平均速度;u′为脉动速度。
3 计算区域的离散及边界条件
为了便于验证数学模型,文章模拟的排沙漏斗模型与吴洋锋等[5]的试验研究中的物理实验模型一致(如图1)。尺寸为进水口高为8.8 mm,宽为44 mm,漏斗室半径为110 mm,锥底坡度为1∶5,排沙底孔孔径为5.5 mm,其中悬板径向坡度i=0。由于进水洞口与悬板之间高度有限,不能无限增大悬板坡度,如果无限增大悬板坡度会影响到进水洞口的运行,所以本文选取了坡度i=0、0.083、0.173、0.259进行了数值模拟,通过在该些悬板坡度下的模拟结果分析,为排沙漏斗优化悬板布置提供参考。悬板置于进水口顶向上14.45 mm的位置,宽度是44 mm,长度是排沙漏斗周长的一半。模拟区域内网格单元划分都为六面体和四面体。控制方程的离散采用有限体积法。从稳定性和精度、适用性方面考虑,选择时间项离散为二阶迎风格式,流项离散为QUICK格式。离散后的线性代数方程组采用交错网格下的PISO算法迭代求解[19]。
进水口采用速度进口边界条件,由进水流量和进水断面面积计算得来,方向垂直于进水断面,速度大小为0.2 m/s。使用随机二维涡量方法给速度加上的非定场扰动k和ε,同时给出非定场扰动k和ε的大小,漏斗室顶部设为空气进口,空气体积数为1;出口分别为悬板上的出流口以及排沙底口,出口所在的边界设置为压力出口,压强的大小与大气压相同为1.013 kPa;壁面采用无滑移边界,近壁处的粘性底层采用壁面函数法。固体颗粒在壁面处的边界条件采用“reflect”边界,在溢流出口处的边界条件采用“escape”边界条件,在底孔出流出处的边界条件采用“trap”边界条件。颗粒与壁面的碰撞恢复系数为1.0。DPM模型的进口设置为不同直径的颗粒射入面,分别计算了直径为0.001、0.005、0.01、0.015、0.025、0.035、0.055、0.085和0.1 mm的泥沙从进口均匀地射入排沙漏斗,颗粒入射流速设为0.2 m/s,质量流量为0.4 g/s,密度为2.03 g/cm3。颗粒相的体积分数为1.27%[20-21]。
虚拟水理论的提出,为区域农业产业结构的合理优化提供了新的视角。以自治区种植业“十三五”规划发展为依据,设定不同的情景,从虚拟水战略对生态环境、水资源消费和社会环境正反方面的影响进行分析。
4 计算结果与分析
4.1 网格敏感性分析
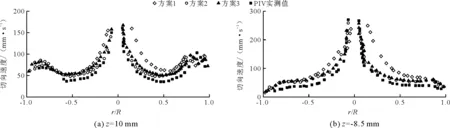
考虑到网格数量对计算结果的影响,文中采用了3种网格划分方案对计算区域进行离散,方案1、方案2、方案3网格总数分别67×104、90×104和110×104。论文采用悬板径向坡度i=0.259时的水平断面z=10 mm、z=-8.5 mm(如图2(a))与90°、270°径向断面相交线(如图2(b))上各点的切向流速计算结果与吴洋锋等[5]的流速实测值进行对比分析,如图3所示。图3中r/k为测点距漏斗中心的径向距离与漏斗室半径的比值。由图3可看出3种网格剖分方案的预测结果与实测结果趋势一致,其中由图3(a)和图3(b)还可以看出切向流速沿径向分布规律为:在柱体区内90度一侧,0.15 1.进水口; 2.悬板始端; 3.溢流悬板; 4.悬板末端; 5.排沙底孔; 6.溢流侧槽; 7.流侧槽出口 图2 测试面示意图 图3 不同网格数量的计算值与PIV实测值对比 根据排沙漏斗内部的清水流场分布特性和排沙漏斗的内部结构,将排沙漏斗划分为柱体区(z>0 mm)和锥体区(z<0 mm)来进行流场分析,如图2(a)所示。 由文献[12]可知x=0和y=0的切向流速分布规律基本一致,因此文章以各水平断面的x=0交线为例来讨论漏斗室内的的切向流速分布规律。图4为不同悬板径向坡度漏斗室内z=24 mm、z=10 mm、z=4.4 mm和z=-8.5 mm上交线x=0上水流切向流速沿径向分布规律。规定切向速度逆时针为正。排沙漏斗的进水口位于图2(b)中z=0和z=8.8 mm之间,悬板位于z=23.25 mm。从图4可以看出,受进流和出流不对称的影响,切向速度沿着径向分布不对称。由图4(b)、4(c)可以看出,不同径向坡度下0.1 从图4可以看出,随着i的增大,不同悬板径向坡度下排沙漏斗柱体区和锥体区的切向流速都是先增大后减小或者趋于恒定。如图4(d)锥体区中z=-8.5 mm,r/R=0.5时切向速度在i=0时为0.062 m/s,当i=0.087和0.173时,切向速度分别为0.125 m/s和0.158 m/s,切向速度增大了101.6%和154.8%。而当i=0.259时,切向流速为0.137 m/s,相比于i=0.173,减小了15.3%。从图4还可以看出悬板径向坡度i=0.173时各个平面上相应的切向流速均为最大值。说明坡度i=0.173排沙漏斗螺旋流的环流强度达到最大,因此该坡度下水沙分离的机率最大。 图4 不同水平测试面上x = 0测线上的切向速度分布 图5为不同悬板径向坡度漏斗室内水平断面z=24 mm、z=10 mm和z=4.4 mm和z=-8.5 mm上交线x=0上水流径向流速沿径向分布规律。规定径向流速指向漏斗室中心为正,负值表明指向漏斗室边壁。 由图5(a)可以看出,位于坡度为i=0的溢流悬板顶部的z=24 mm水平断面上的径向流速基本是指向漏斗室边壁或者为零,当溢流悬板自漏斗边墙向漏斗室中心倾斜坡度增大,溢流悬板对上方水体存在着一个指向漏斗室中心的作用力,导致坡度i=0.087、i=0.173、i=0.259的溢流悬板顶部的z=24 mm水平断面上的径向流速基本是指向漏斗室中心,对比分析会发现和坡度i=0相比,悬板坡度为i=0.087、i=0.173、i=0.259会使泥沙向室内运动,不易在悬板上淤积。同时由图5(a)还可以看出坡度i=0.173和i=0.259的排沙漏斗中大部分区域存在着很大的正向径向流速,说明在坡度i=0.173和i=0.259下溢流悬板对上方水体的指向漏斗中心的作用力相比坡度i=0、i=0.087要大,泥沙更容易向室内运动,更不易于在悬板上淤积。 由排沙漏斗的水沙分离原理可知,径向速度是压差力和离心力大小的直接反映。由图5(b)可知,在r/R坐标轴的负半轴上的x=0测线上各点的径向流速为负值,说明该区域的水流向漏斗边墙处运动,而图5(c)和(d)中z=4.4 mm和z=-8.5 mm大部分径向流速为正值,说明该区域的水流向漏斗中心运动,以上分析可得r/R坐标轴的负半轴对应的漏斗区域内产生了二次流,由于二次流的作用下该区域上方水流向漏斗室边壁运动,同时在该区域贴近漏斗室底坡的下层区域形成较大的向内的径向流速,其中由图5(b)和(d)发现在该区域靠近最上方坡度i=0.173存在最大的负方向径向流速,靠近最下方坡度i=0.173存在较大的正方向径向流速,分析可得坡度i=0.173最有利于二次流的产生。 图6表示不同悬板径向坡度漏斗室内不同垂直断面上的垂向流速沿径向的分布规律,其中规定垂向速度沿Z轴正半轴为正(方向向上),沿Z轴负半轴为负(方向向下)。 由图6(a)、6(b)、6(c)对比看出随着i越大,悬板附近的垂向流速方向向上的区域面积越小;由图6(c)、6(d)随着i增大,悬板上附近的轴向流速方向向上的区域面积增多,但由图6(a)、6(b)、6(d)还可以发现图6(d)悬板附近的轴向流速大,方向向上的区域面积较图6(a)、6(b)要少。说明悬板坡度i=0.259下泥沙较不易于悬浮到悬板上方,同时进入下游的可能性较低和淤积在悬板上的含量较少;悬板坡度i=0.173下泥沙最不易于悬浮到悬板上方,同时进入下游的可能性最低和淤积在悬板上的含量最少。 图5 不同水平测试面中x=0测线的径向速度分布 应用DPM模型模拟了溢流悬板径向坡度不同的排沙漏斗对直径d分别为0.001、0.005、0.01、0.015、0.025、0.035、0.055、0.085和0.1 mm的颗粒截除率,结果见表1。表1中颗粒截除率应用公式(10)计算。 (10) 式中:η为截除率;n为颗粒被捕捉个数;M为颗粒射入总个数。 从表1可知,在同一悬板径向坡度下,颗粒截除率随着泥沙的颗粒粒径的增大而增大;处理同一粒径的颗粒时,颗粒截除率并不是随着悬板的径向坡度的增大而增大,如粒径0.001 mm时,i=0、0.087、0.173、0.259时的截除率分别是64.3%、64.3%、65.4%、60.1%。显然,悬板径向坡度i=0.173时的排沙漏斗截除率最高。由前文的流场分析结果也可知,相较其他坡度而言,i=0.173时漏斗室内切向流速最大,有利于水沙的离心分离,同时,该坡度下二次流使锥体区内产生了较大的正方向径向流速,因而能够提供较大的指向漏斗室中心径向流速,有利于泥沙颗粒输运至排沙底孔;较其他坡度下不利于泥沙在溢流悬板上淤积,因而减少泥沙从溢流侧槽出口流出,使泥沙更多的从排沙底孔排除。因此,排沙漏斗截除率随着悬板坡度的增大而在一定范围内增高,并不是随着坡度的增大而无限增大,存在一临界的悬板坡度使排沙漏斗的截除率达到最大值。 图6 不同径向坡度下的不同垂直断面上的垂向速度分布 表1 悬板径向坡度不同时排沙漏斗对不同直径颗粒的截除率% 耦合大涡模拟和VOF方法对改变悬板径向坡度的排沙漏斗内部流场进行了数值模拟,根据计算结果对悬板径向坡度改变时流场特性和对水沙分离的影响进行了分析,并通过DPM模型计算了各径向坡度下漏斗对各级粒径颗粒截除率分离效率。主要得出如下结论: (1)悬板径向坡度i=0.173时切向流速达到最大,室内环流强度继而也达到最大。随着i的增大,不同悬板径向坡度下排沙漏斗柱体区和锥体区的切向流速都是先增大后减小或者趋于恒定,因此室内涡流强度并不是随着悬板径向坡度的增大而单调增加,存在一临界的坡度使室内涡流强度达到最大值。 (2)受进流和出流不对称的影响,切向速度沿着径向分布不对称。悬板上方溢流区和锥体区具有相同的涡流特征,越靠近边壁切向流速越小;柱体区(进水涵洞底板以上至悬板)范围内具有相同的涡流特征,越靠近边壁切向流速越大。 (3)悬板坡度i=0.259下泥沙较不易于悬浮到悬板上方,同时进入下游的可能性较低和淤积在悬板上的含量较少;悬板坡度i=0.173下泥沙最不易于悬浮到悬板上方,同时进入下游的可能性最低和淤积在悬板上的含量最少。 (4)文章中悬板径向坡度为i=0.173时的泥沙截除率,比悬板其他径向坡度的泥沙截除率要大。排沙漏斗截除率随着悬板坡度的增大而在一定范围内增高,并不是随着坡度的增大而无限增大,存在一临界的悬板坡度使排沙漏斗的截除率达到最大值。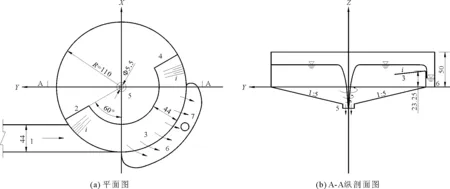

4.2 切向流速分布特征

4.3 径向流速分布特征
4.4 垂向流速分布特征

5 不同粒径颗粒截除率结果与分析


6 结 论
