小波分析在土石坝位移混合模型中的应用

王 卓

(山西省水利水电勘测设计研究院，山西 太原 030024)

工程应用较广的大坝安全监控数学模型首推应用数理统计分析方法建立的大坝安全监控回归模型，数理统计方法不能对大坝的影响因子做出合理的物理解释[1]。混合模型介于统计模型和确定性模型之间，既具备统计性质，又可以反映大坝的物理力学工作状态[4]。混合模型建模受时域限制较小，外延功能较强，拟合精度、预测精度较高，而且，模型水压因子的物理意义明确，时效位移分量的敛散性容易判别，对大坝运行监控的针对性较强，容易做到心中有数[2]。

1 有限元模型

本文使用了MIDAS/GTS岩土与隧道分析软件中的邓肯-张E-B模型对某沥青混凝土心墙堆石坝进行了三维有限元建模。在进行有限元计算时，认为沥青混凝土心墙与坝体堆石同步填筑上升，荷载采用逐级施加方式[3]。加荷过程中，模拟第一次蓄水，坝体施工到2605.00m高程处时，分2级蓄水到2600.00m高程停止蓄水，继续填筑坝体直到坝顶。坝体填筑完成后，分2级蓄水到正常蓄水位2650.00m高程。在蓄水到正常蓄水位以后，库水位分7级消落到死水位2600.00m高程，以建立坝体位移与库水位的关系。考虑模型中仪器埋设位置应与实际吻合，整个模型自由剖分，采用四面体单元，网格节点总数为：31938个，单元总数为：158729个，包括坝体、地基和周围山体，其中地基和周围山体50206个，坝体108523个。

2 小波分解

2.1 小波分解基本原理[5- 7]

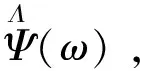
(1)

则称Ψ(t)为一基本小波或母小波。将母函数Ψ(t)经伸缩和平移后，就可得到一个小波序列。对于连续的情况，小波序列为：

(2)

式中，a—伸缩因子；b—平移因子。

对于离散的情况，小波序列为：

Ψj，k(t)=2-j/2Ψ(2-jt-k)j，k∈Z

(3)

对于任意函数f(t)∈L2(R)的连续小波变换为：

(4)

其逆变换为：

(5)

根据多分辨分析理论，如果二进制离散小波函数族{Ψj，k(t)，j，k∈Z}构成L2(R)中的标准正交基，对于时变信号f(t)∈L2(R)有如下的正交小波分解：

(6)

式中，N—分解层数；dj，k—小波分解系数；cj，k—尺度分解系数。

2.2 大坝安全监测数据时效分量提取

就大坝的变形监测数据而言，大坝位移监测数值包含两个部分：一是弹性位移，另外一个是随时间和荷载而变的非线性位移，俗称时效。它包括坝体混凝土和基岩的徐变以及坝基的裂隙、节理和其它软弱构造等在水压力作用下发生的压缩和塑性变形。时效分量[8]的变化规律一定程度上反映了大坝的运行性态。一般正常运行的大坝，在蓄水初期时效变化较大，运行多年后趋于稳定。如果时效分量突然变大或变化急剧时，这就是大坝或坝基病态工作的征兆。所以，研究时效分量的提取并对其进行分析，在大坝安全监测资料分析中有重要的作用。

目前通常采用的确定时效分量的方法是，事先选定好与时间有关的因子，对变形监测数据进行回归分析，进而求得时效分量。这种事先拟定时效因子构造形式的方法带有一定的人为影响，有时不一定准确。另外，当水位、温度等因子与时效密切相关时，这种相关性对回归分析产生较大的影响，也会影响时效分量的提取效果。针对这些问题，本文结合小波分析，对大坝安全监测数据的时效分量进行提取研究。时效分量变化的部分通常表现为长周期、低频率的变化。利用小波分析提取时效分量，首先是对大坝监测信号进行小波分解，滤除随机的高频变化成分和随库水位、气温而周期变化的成分，剩下的低频部分就可代表大坝监测数据系列的发展趋势(时效)。

3 位移混合模型基本原理

大坝变形统计回归数学模型中，效应量可分解为变形水压位移分量、变形温度位移分量、变形时效位移分量。

3.1 水压位移分量

水压分量δH(t)是在水压荷载作用下，由于坝体、坝基和库区岩石产生变形而引起效应量的弹性或可恢复变化部分。这种关系可用一元多项式来描述，即：

(7)

式中，H(t)—观测日水位；H0—基准水位；ai—回归系数。

根据有限元计算结果，利用式(7)，采用最小二乘估计法得到式中各项系数，建立水压位移分量确定性模型。

3.2 温度位移分量

本文温度位移分量用统计回归求得，模型因子考虑气温的滞后效应，温度位移分量模型具体形式如下：

(8)

式中，Ti(t)—i=1、2、3、4、5分别是观测日当天气温，观测日前7、15、30、60d的平均日气温；bi—回归系数。

3.3 时效位移分量

大坝安全监测的信号通常会受到噪声的污染，其中的噪声主要是由于随机因素及观测误差的原因而产生的[9]。为了从信号中提取出表征被检测对象特征的有用信息，提高模型的拟合精度和预报性能，有必要对信号进行降噪处理。

大坝安全监测的信号序列，有用的信号通常表现为低频部分或是一些比较平稳的信号，而噪声信号通常是表现为高频信号，所以利用小波分析对信号进行降噪可以按如下方法处理[10]。

(1)信号的分解。选择小波并确定小波分解的层次N，然后对信号进行N层小波分解。

(2)小波分解高频系数的阈值量化。从第1层到第N层的每一层高频系数选择一个阈值进行软阈值量化处理。

(3)小波的重构。根据小波分解的第N层的低频系数和经过量化处理后的第1层到第N层的高频系数，进行小波的重构。在这3个步骤中，最关键的就是如何选择阈值和如何进行阈值的量化，本文采用的是最优预测变量阈值选择：如果信噪比很小，则估计有很大的噪声，就采取固定的阈值，阈值大小为sqrt(2*log(length(f(t))))，其中f(t)为进行分析的大坝安全监测信号；否则基于史坦的无偏似然估计原理的自适应阈值选择2。这种阈值选择的方法即能较好的进行降噪处理，又可以把高频部分的弱小的有用信号保留下来。

3.4 位移混合模型的建立

效应量模型构造形式如下：

δ(t)=λ1δH(t)+δT(t)+λ2δθ(t)+c

(9)

即：

(10)

式中，λ1—水压位移分量修正系数，λ2—时效位移分量修正系数。

欲建立以上位移混合模型，关键是求修正系数λ1、λ2、系数ai(i=1、2、3)、bi(i=1、2、3、4、5)以及c。系数ai已经由有限元计算求得，其他系数由最小二乘法估计。

将观测日的水位H(t)、温度Ti(t)以及计算得到的时效位移分量δθ(t)代入式(10)中，得到：

δ(t)=fi(λ1，bi，λ2，c)

(11)

式(11)为参数λ1、bi、λ2的形函数。

δ(t)与实测值δ0(t)的残差平方和为：

Q=∑(δ0(t)-δ(t))2=F(λ1，bi，λ2，c)

(12)

要使Q最小，则必须满足下列条件：

(13)

由式(13)求得系数λ1，bi，λ2，c，从而得到位移混合模型。

4 水平位移的混合数值模型及其成果分析

本文对某沥青混凝土心墙堆石坝的TP08、TP11、TP18、TP23号测点建立了水平位移混合模型。其中TP08位于坝顶上游侧0-008.5m，坝桩号为0+220m；TP11位于坝顶上游侧0-003.7m，坝桩号为0+320m；TP18位于坝顶上游侧0-005.2m，坝桩号为0+220m；TP23位于下游马道2624.5m高程，坝桩号为0+220m。下面是建立的水平位移混合模型的成果。

4.1 混合数值模型

应用式(9)对上述测点的水平位移观测资料建立混合数值模型。各测点水平位移混合数值模型的各回归系数、时效位移收敛值、复相关系数R、标准差S及S占测值最大值比例见表1。

4.2 各分量对坝顶水平位移的影响分析

由表1可见，大坝位移计算值与水压相关性较高，复相关系数均在0.95左右，剩余标准差较小，精度比较理想。对于本工程沥青混凝土心墙堆石坝来说，坝体各测点顺河向水平位移与水头的一次方不相关，与水头的二次方负相关，与水头的三次方正相关。温度分量与位移呈负相关，即温度上升，坝体向上游变形；温度下降，坝体向下游变形。通过分析用小波分析理论将所选时间段内实测值的时效位移分量提取出来的结果可知，对于本工程沥青混凝土心墙堆石坝来说，坝体各测点时效分量均收敛。

表1 大坝水平位移混合模型系数表

注：表中R表示复相关系数，S表示剩余标准差

4.3 拟合效果分析

所建立的位移混合模型中，有3个测点的复相关系数大于90%，所有测点的剩余标准差都较小，占相应测点测值最大值的比例均小于20%。由此可见，所建立的位移混合模型拟合精度较高，满足工程要求。根据各测点的位移混合模型方程，可求出拟合值、时效位移分量和残差，并将其和实测值绘于同一张图中，得到各测点的实测值、拟合值过程线，如图1—4所示。由图也可以看出，拟合值与实测值基本一致，残差均小于20mm。本文选用本工程大坝前3年半的实测值来提取时效分量，因此在所选用的时间段内，时效分量呈增大趋势。

图1 顺河向水平位移测点TP08实测值、拟合值过程线

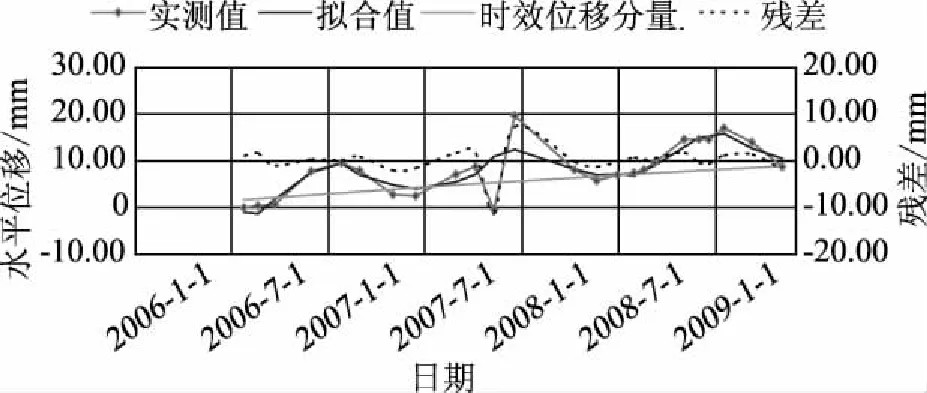
图2 顺河向水平位移测点TP11实测值、拟合值过程线

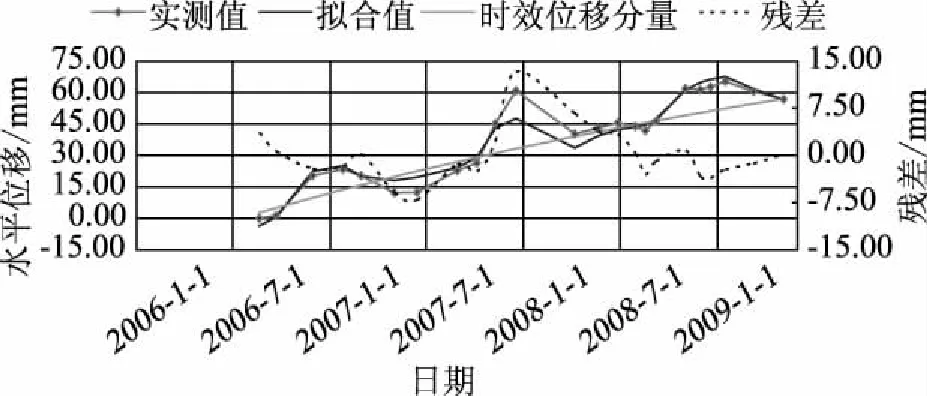
图3 顺河向水平位移测点TP18实测值、拟合值过程线

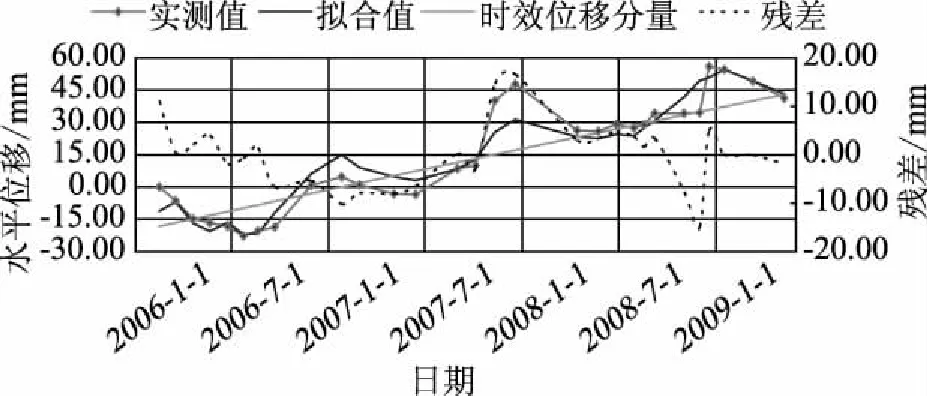
图4 顺河向水平位移测点TP23实测值、拟合值过程线

4.4 预测精度检验

5 结语

本文利用有限元建模分析了大坝不同水位的水平位移，得到水平位移与水位的关系表达式，且用小波分析理论提取出了水平位移时效分量，在此基础上建立了大坝水平位移混合模型。结果表明回归方程拟合效果良好。

由于大坝结构、工作条件及影响因素等的复杂性，仅通过建立效应量和原因量的混合模型还是不够的，需要通过对大坝各种资料，包括设计、施工、运行、检查和观测等资料，进行不同层次的分析并建立相应模型进行比较验证。而且大坝和坝基在运行过程中随着时间推移，条件不断变化，尤其是采取工程措施和遭遇特殊的荷载工况时，因此，监控指标应相隔一段时间后进行校验和修正。当测值接近或者超过历史最大值时，必须认真分析原因，采取相应措施，确保大坝的安全。