基于非结构网格求解器的DES和DDES数值模拟研究
2019-03-26唐海龙
韩 涛,唐海龙
(1.海军驻沈阳地区航空军事代表室,沈阳 110034;2.中国航空工业空气动力研究院 计算流体力学中心,沈阳 110034)
当前工业界和研究中所使用的主要CFD手段仍然是求解RANS方程并附加湍流模型,这种根据统计学原理来重点研究流动平均量的研究方法的精准度主要取决于湍流模型能否合理地描述被模拟的流动特征。目前湍流模型对于包含物面边界的附着流或小分离流动大多效果较好、鲁棒性强,而且模型大多通过固壁的物面率(Law of the wall)来对其中的经验性参数进行校准,但对于自由剪切流动的模拟效果相对较差,至于对中等/大分离或强漩涡的非定常流动来说,RANS基本不能准确模拟。
大涡模拟(LES)被认为是唯一有希望解决大分离流动的数值模拟的技术,然而,尽管LES方法起源较早,但它在网格解析度和时间分辨率等方面的要求所带来了巨大的计算量,使其在目前实际工业问题中无法应用。
最初,有的学者为了降低LES的计算量,尝试在粗网格下应用LES(Very large LES-VLES)方法[2],没有获得成功。但其以最小代价捕捉流场中大尺度的非定常现象和相干结构的思想是非常诱人的,这也成为许多混合LES/RANS方法发展的目的。Hybrid LES/RANS方法就是为了搭建在工程应用环境下RANS方法和LES方法所存鸿沟之间的桥梁,克服RANS模型对复杂分离流动模拟的能力不足和LES巨大计算量的问题,分别将各自的优势进行巧妙的组合应用于解决中等/大分离条件下的流动模拟问题。
基于非结构网格的UNSMB计算平台是具备大规模并行计算能力,包含多种二阶精度的空间和时间格式及大量湍流模型的内部代码。当前在该平台的解算器框架下开展了以下工作:通过对湍流模拟方程的求解形式进行改造,使其在同一的求解框架下既具备RANS分支,也包含LES分支,其湍流模拟方式的切换是通过对计算域中湍流尺度的判断来完成的。本次混合LES/RANS方法的研究主要集中在基于DES类的SA-DES和SA-DDES的模块开发,使其具备复杂大分离流动的模拟能力。下面将围绕这两个混合模型的模块开发和相应的算例验证进行介绍。
1 混合LES/RANS模拟方法介绍
1.1 基于Navier-Stokes方法的解算器
UMSMB求解平台是基于非结构对偶网格、采用格点有限体积法,求解可压缩Euler/NS方程的CFD求解器。其解算的方程组可以简单写为
(1)
式(1)中,C和D分别代表对流和粘性通量项,而S表示源项;式(1)中的解矢量q为守恒变量,q=[ρ,ρu,ρv,ρw,ρE,ρφ]T,其中,ρ为密度,u、v、w为3个方向上的速度分量,E为总能量,φ代表所求解的湍流变量。
UNSMB求解器可应用于非搭接的任意网格单元形式,为基于边的迭代求解方式,通过代码的前处理程序将结构、非结构和杂交网格中基于单元点的信息处理成UNSMB能辨识的基于边的信息系统,从而构造了以原始网格格点为中心的离散控制体。
将式(1)所表示的基本控制方程对任意控制体(Ω)及其的边界(S)进行积分,得到基本的计算格式为
(2)
时间相关的推进格式是通过双时间步长方法[5]来完成,包含一个全局的物理时间步长(Δt)和一个应用于三阶龙格库塔格式内迭代的虚拟当地时间步长(Δτ)。将式(2)所表示的流动控制方程改写为时间导数项和和残值项R(q),它包括对流、扩散通量项和源项,即R(q)={C(q)+D(q)-Sq}。通过引入虚拟时间(τ),非定常的N-S方程改写为
(3)
在当前的计算中,物理时间导数的离散通过三点后差的格式得到,其二阶精度的计算格式为
(4)
在每个时间步Δt中,都是通过三阶龙格库塔推进算法来迭代求解,但物理扩散项仅在第一步进行计算。虚拟时间步长的选择需要受到物理真实步长的限制,为
(5)
此处,Δτ0表示为满足稳定性问题所确定的当地时间步长;CFLv是粘性CFL数,为UNSMB中用户自己输入的参数(CFLVIS)。此外,还通过隐式残值光顺和多重网格来加速收敛,并通过MPI通信技术来实现大型并行计算。
1.2 Spalart-Allmaras RANS模型

(6)
此处不考虑转捩相关项,至于详细的模型常数和经验函数就不在此赘述了。
1.3 SA-DES模型
大涡模拟在模拟湍流的细节和流动分离等方面都有很好的精准度,但其对高雷诺数下物面流动的计算量是当前计算机水平所不能企及的,故其距工程应用还有相当大的距离。RANS方法对湍流的模拟是通过湍流模型来完成的,不能解析任何湍流细节,反映的是平均流动的变化情况,但RANS方法的高效性和鲁棒性使其在工业界得到广泛的应用。并且两种模型方法的求解方程相似度很高,以雷诺平均速度〈ui〉的输送方程为例,即
(7)
(8)
通过对比可以明显看出公式(7)和公式(8)非常相似,可以在同一解算器中应用相同的程序框架来实现。再对LES方法中应用涡粘性假设的SGS湍流模型进行分析会发现大多数的SGS模型的推导都来源于RANS模型,为RANS模型的对应物。因此,LES方法和RANS方法不仅主控方程结构相似,而且湍流模型也相似。于是有人提出了分别应用RANS和LES优势的混合LES/RANS模型方法,即在近物面应用RANS模型,远离物面的分离区域应用LES模型进行解析湍流。
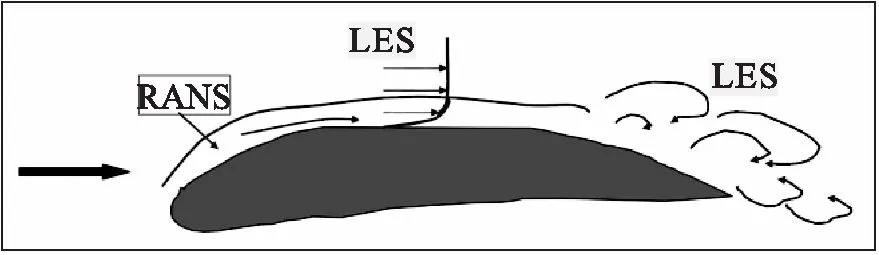
图1 DES方法的示意草图
Spalart等人通过对SA模型进行如下的修改完成了最早DES格式的设计(如图1所示),也即被广泛称之为DES97格式[7]。
Δ=max{Δx;Δy;Δz}
(9)
通过各项同性湍流算例的校准得到模型参数Cdes=0.65,有文献研究表明数值结果对该参数不是很敏感。
(2)对模型方程中长度尺度进行了如下修改
(10)
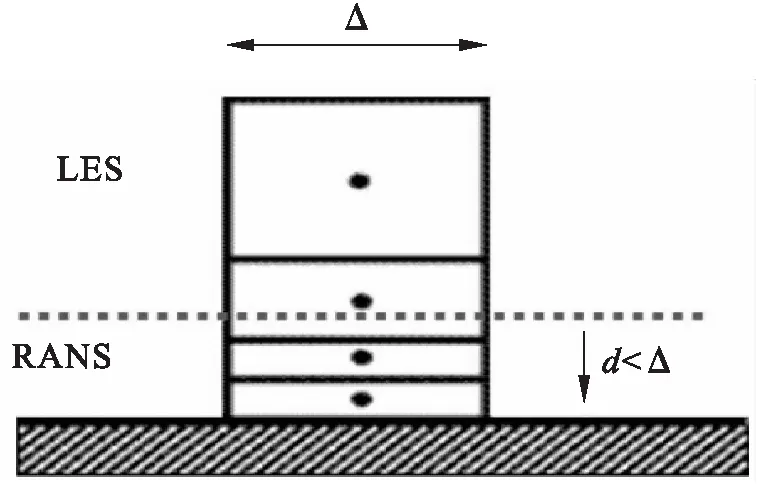
图2 DES方法中RANS和LES模式切换图示
如图2所示:(1)近壁面的长度尺度的增长不能超出RANS的计算区域,在贴近物面处d
Spalart等人创造“脱体涡模拟”(Detached Eddy Simulation-DES)术语来命名这种方法,其主要目的是将流场的求解方法进行混合,在外部流动区域应用LES,应用LES模式来解析远离所有边界的脱体涡,与此同时在近壁面流动区域应用RANS模型。应用RANS模型的目的是为了得到近壁面流动在统计意义上的合理描述,其计算网格仅需在物面法向加密,而在切向可应用相对较粗的网格。此外,这两种方法的切换是通过一个自动的判据来完成,从而避免需要用户事先指定。
公式(9)的提出是基于在LES方法中最粗网格步长决定了可解析涡结构最小尺度。这个问题在LES方法中比混合LES/RANS方法更突出,它影响LES/RANS的交界面。文献[8]中对公式(9)式进行了详细的讨论,图1~2所示网格类型是一种针对DES方法来说比较安全的网格形式。
1.4 SA-DDES模型
自1997年Spalart等人提出DES方法以来,混合LES/RANS方法就一直被当作工程CFD计算中解决复杂漩涡运动和分离流动问题的最合适的手段,引起了工业界和学术界的广泛研究,其不完善的地方还有很多,远未成熟。
早期DES方法在薄的边界层可以很好地模拟真实的流动现象,但在模拟厚边界层和浅分离区域时可能会出现一些错误的行为,主要出现在当平行于物面的网格间距Δ‖小于边界层厚度δ时(如图3所示),这种现象既可能是由网格加密引起也可能是边界层本身就比较厚引起的。当DES网格加密使得长度尺度进入LES分支时(涡粘性低于RANS的水平),由速度脉动分辨得到的解析雷诺应力不能替代模化的雷诺应力。雷诺应力的亏空[8]降低了表面的摩擦力,可能导致由网格所诱导的流动提前分离。
为了避免在附着流中出现非物理现象,消除DES方法对网格的限制,在边界层内保存RANS特性,物面的网格间距Δ‖与边界层厚度δ无关,减小灰色区域。Spalart等人[9]通过加入一个函数fd来重新定义耗散长度尺度

图3 模糊的DES网格类型
(11)
此处
fd=1-tanh[(8rd)3]
(12)
及
(13)
2 算例测试和验证
前面介绍了我院开发SA-DES和SA-DDES程序模块的相关情况,下面将通过一系列的测试算例和工程算例来检测和验证该模块的数值模拟能力。
2.1 NACA0012翼型的算例
翼型的动态失速是一个伴随流动分离的典型非定常不稳定过程,失速涡在前缘附近已经形成,并沿着翼型表面移动和增长,最终在翼型后缘附近产生分离,脱离翼型表面,这种分离流动的动态变化影响了机翼升力的产生。
本节将采用SA-DES和SA-DDES来模拟翼型的动态失速运动,测试程序模块的有效性,并与URANS的计算结果进行对比分析。
2.1.1 计算模型及网格
本次测试计算应用NACA12翼型作为计算模型,展向拉伸1倍弦长,弦长为0.1 m。使用POINTWISE生成O-型结构网格,网格数量为225×191×31,展向均布31层,为了精确捕捉附面层内的流动,网格第一层高度为1×10-6,y+均小于1。图4为部分网格视图。
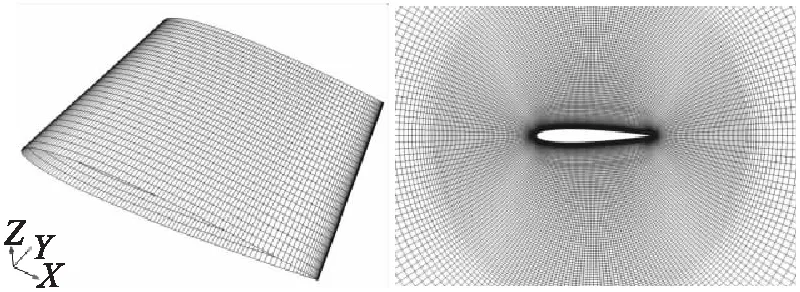
图4 NACA0012翼型的表面及空间网格
2.1.2 数值模拟的时间历程分析
本算例将开展NACA0012翼型在45°失速攻角下的研究,并将计算结果与试验数据[10,11]和Hong-silk IM[12]的DDES计算结果进行对比分析。计算状态为Ma=0.50,Alpha=45°,基于弦长的雷诺数Re=1.3×106。分别进行了基于URANS、DES和DDES的3种非定常模拟方法研究,其物理时间步长均设置为0.02T0,为1.2×10-5,T0为来流的特征时间尺度。由于DDES模拟方法对初场敏感,因此,本次计算中均以自由来流作为初场值,均大致计算400T0时长。
图5描述了UNSMB代码DDES数值计算的残值收敛过程。该图表明计算的收敛性很好,呈现了明显的周期性,其表示为上翼面漩涡的脱离周期,不过该 DDES的幅值随时间变化,有一定的混沌现象。

图5 DDES计算的密度收敛历程
2.1.3 数值模拟的时均结果分析
图6表明3种模拟结果从100T0开始对瞬态阻力系数进行平均,直至400T0,其时均阻力系数最后均趋于常数,不过URANS的阻力波动幅度大,时均值变化较为缓慢,而DES和DDES的变化速度较快,大致在250T0时就基本不变。NACA0012翼型45°攻角下试验[10,11]的时均阻力为1.075, UNSMB计算的为CDURANS=0.979,CDDES=1.110,CDDDES=1.078。通过与试验结果的对比表明,DDES计算结果与试验值的吻合度非常高,仅高0.28%,而DES结果大了3.3%,且URANS的计算结果与试验值的差值也不是特别多,充分表明UNSMB代码对大分离流动的模拟准度较好,其中DES模拟结果的稍差可能是由于翼型表面的弦向网格分布过密所导致。
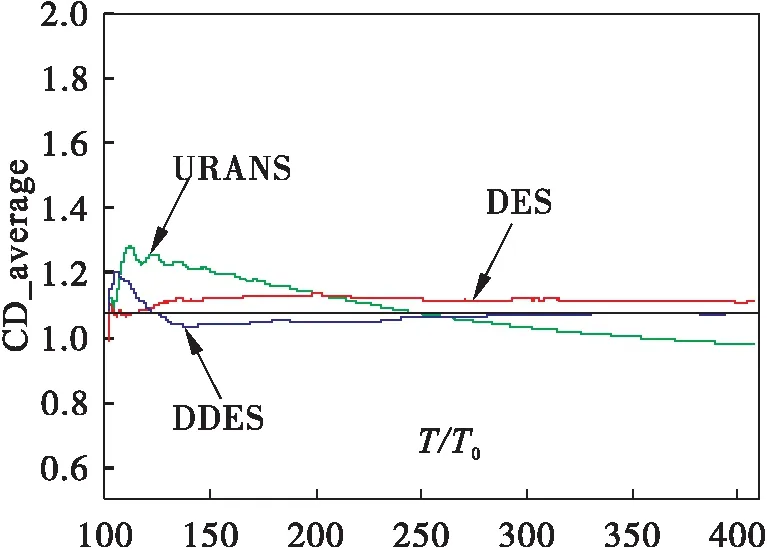
图6 时均阻力系数比较
2.1.4 数值模拟的瞬态流场分析
下面将对3种模拟方法的瞬态流场进行简要地分析,以展向50%长度中截面作为研究对象,分别选取两个典型时刻进行比较。
图7为3种模拟方法的瞬态流场图,通过应用湍流涡粘性系数对剖面进行染色,反映了尾迹区的运动。通过3组图像的对比可以看出,收敛后的URANS瞬态流动变化较小,更多地体现RANS的特性,而DES和DDES可以清晰地分辨出尾迹漩涡的运动过程,解析的漩涡尺度更小,流动是在翼型的后缘卷起再脱离上表面。此外,通过对等值面的量值比较可以发现URANS计算的湍流涡粘系数比DES和DDES大得多,而DDES的涡粘系数最小,这说明URANS的数值耗散太大,尾迹中流动的脉动量被快速抹平,但DES和DDES中较小的湍流涡粘性系数就可以较好地模拟尾迹区的流动特征。
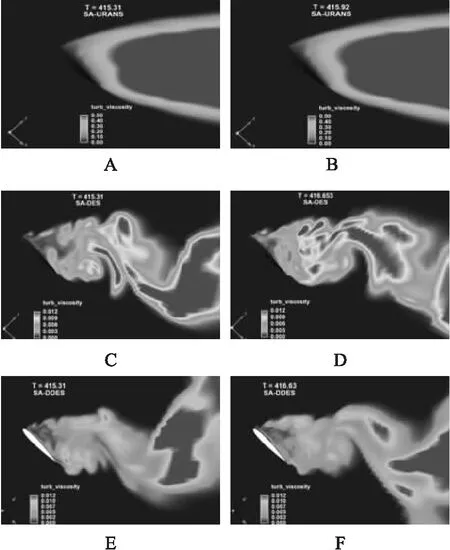
图7 URANS(A、B)和DES(C、D)及DDES(E、F)的瞬态流场图
2.2 钝前缘三角翼的算例验证
在2001年,北约RTO AVT-113工作团队提出了第二届“国际漩涡流动试验”(VFE-2)[13]的研究项目,进行了大量的试验和CFD计算研究,目的是为了拓展对三角翼流动拓扑和物理现象的认识及对计算代码的验证和确认。下面我们将通过对中等前缘钝度的VFE-2构型进行DES计算来验证代码的可靠性。
2.2.1 计算模型和网格
VFE-2模型为一个带尾撑的薄三角翼,包含4个可换的前缘(1个尖前缘和3个钝前缘),如图8所示。

图8 计算模型的正视图
根据国外对VFE-2的研究表明,1200万单元的网格就足够的。本次计算使用ICEM CFD生成结构网格,第一层高度为1×10-6,附面层内网格保持在30~50重左右;大部分y+都在1左右,仅很少部分的y+>1,且最大值为2.9。

图9 计算网格全局视图和对称面部分视图
2.2.2 DES模拟结果
本算例主要使用SA-DES来进行验证计算,其计算状态为Ma=0.4,Alpha=13.3°,基于平均气动弦长的雷诺数Rmac=3×106,其时间步长设置为Δt=2.5×10-5。该计算状态为高亚音速小分离流动状态,在距离顶点一段距离的位置流动产生分离,且二次涡的旋转方向与主涡相同。模拟该类流动最大的难点在于前缘分离点的位置,以及主涡及二次涡的展向位置及大小。
图10为对DES瞬态计算结果在某一时间历程内进行时均后的结果分析,其流动结构和定常计算结果类似,右侧图可以看出内侧二次涡较早的形成,但强度很低。

图10 SA-DES计算得到上表面Cp分布和等截面的总压恢复等值线图
2.2.3 流动拓扑结构分析
图11显示的是亚声速下三角翼的压力云图和表面摩擦力线图,该图可以增加我们对钝前缘三角翼流动拓扑的理解。分离线是从前缘开始的,但并没有延伸到机翼的顶点位置,一旦分离产生,自由剪切层就对流至机翼上表面,从而在近物面得到一个压力较低和旋度较强的区域,导致了外侧主涡的产生。

图11 表面极限流线和压力分布
3 结论
本文主要阐述了UNSMB代码的混合LES/RANS模块的开发研究,其湍流模型为SA-DES和SA-DDES,并分别介绍了混合模块相关的理论和验证算例分析。计算结果表明,UNSMB的DES和DDES模块可以应用于大分离流动及复杂漩涡运动的数值模拟计算,并具备良好的计算精准度,可以解析和捕捉由流场内部自身所诱导的强非定常运动和漩涡结构。该混合模块在CFD理论研究和工程计算中都具备广阔的应用前景,可以满足该项目所要求的飞机结冰后气动力性能评估的要求。
