两法解决平衡的稳定性问题
2019-03-26
(绍兴市第一中学,浙江 绍兴 312000)
物体的平衡状态可分为稳定平衡、不稳定平衡和随遇平衡.在高中物理竞赛教学中,经常要求求解物体的平衡位置,并对其平衡的稳定性进行分析讨论.对于这类问题,一般可以用以下两种方法进行求解.
1 力矩法
处于平衡状态的物体,若受到外界扰动而偏离平衡位置,将产生合外力力矩.如果合外力力矩是一个回复力矩,即此合外力力矩有把物体拉回原平衡位置的倾向,那么物体的平衡为稳定平衡;如果合外力力矩有把物体推离平衡位置的倾向,那么物体的平衡为不稳定平衡;如果既没有回复原位又没有远离原位的倾向,那么物体的平衡为随遇平衡.
力矩法,即先通过力矩平衡找到平衡位置;再考虑偏离平衡位置后,偏移量的方向与所受合外力力矩的方向的关系,从而来判断物体的平衡稳定性.
例题.如图1所示,半径为R的圆环绕其铅垂直径以不变的角速度ω匀速转动.两质量为m的珠子用长为L=R的轻杆相连,套在圆环上可以无摩擦地滑动.试求轻杆在圆环上的平衡位置,用环心O与杆中点C的连线与竖直轴的夹角θ表示,并分析平衡的稳定性.[1]

图1 图2
解析:(1) 先求轻杆在圆环上的平衡位置.
取随环匀速转动的参考系,轻杆与珠子组成的系统处于平衡状态,系统受到重力2mg、环对两小球指向环心的弹力N1、N2,以及惯性离心力f1、f2,受力分析如图2所示,其中作用在上、下端珠子的惯性力f1、f2分别为
f1=mω2Rsin(θ+30°),
f2=mω2Rsin(θ-30°).
对竖直轴,系统所受合外力力矩为M=MG+Mf1+Mf2,其中
代入化简可得
平衡时有M=0,解此方程,得系统平衡位置.


(2) 讨论平衡位置的稳定性.
微扰令系统偏离平衡位置,讨论偏移量dθ的正负与对应合外力力矩M的正负关系.若偏离平衡位置时,合外力力矩M一直为0,则为随遇平衡;若偏离平衡位置的偏移量dθ的正负与合外力力矩M的正负一致,则为不稳定平衡;相反的,则为稳定平衡.


表1


2 势能函数法
下面用势能函数法重解上述例题.
取随环匀速转动的参考系,轻杆与珠子组成的系统处于平衡状态,通过受力分析可知,该例中系统的势能包含重力2mg对应的重力势能Epg、惯性离心力f1和f2对应的离心势能Ef1及Ef2.

同理,下端的珠子的离心势能为
其中,r1=Rsin(θ+30°),r2=Rsin(θ-30°).
从而有系统的势能E(θ)=Epg+Ef1+Ef2,即

从图中可知,势能函数的极值点对应平衡位置,如图3的A点和B点,图4的C点、D点和E点;势能函数的极大值位置对应不稳定平衡位置,如图3的B点,图4的C点和E点;势能函数的极小值对应稳定平衡位置,如图3的A点和图4的D点.
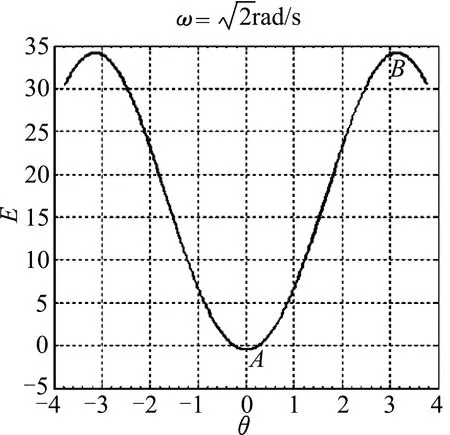
图3 势能函数图
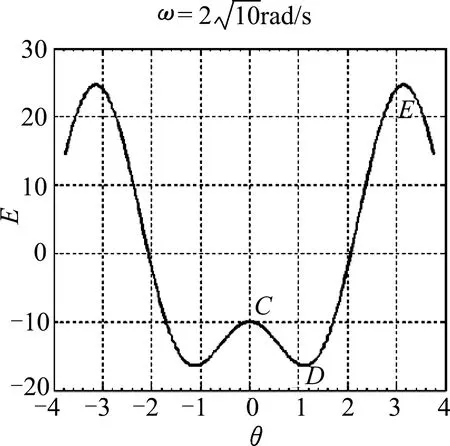
图4 势能函数图
因此可以令势能函数对广义坐标的一阶导数等于零,来求得平衡位置;然后利用势能函数对广义坐标的二阶导数在平衡位置取值的正负来判断平衡是属于稳定平衡还是不稳定平衡.


结论与方法1一致.
为讨论平衡位置的稳定性,计算势能函数对广义坐标的二阶导数,有

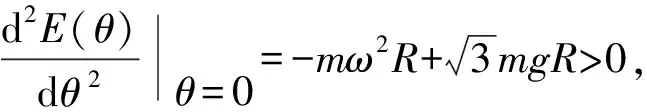
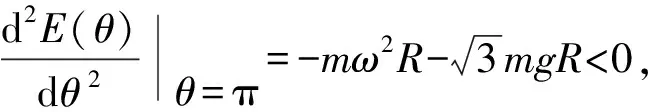

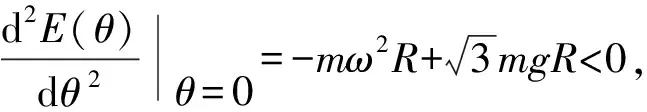
取极小值,属于稳定平衡.
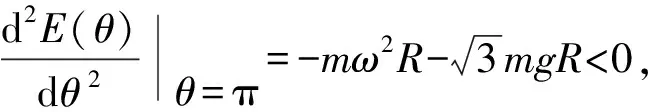
3 方法应用

图5
如图5所示,杆长l=a+b,质心在C点,杆的A、B两端分别支于互相垂直的两个光滑斜面上而处于平衡.试求出杆的平衡位置,并分析平衡的稳定性.
