蓝印花布纹样建模与重构

陶 晨， 段亚峰， 徐蓉蓉， 杨剑平， 周 赳

(1. 绍兴文理学院 纺织服装学院， 浙江 绍兴 312000； 2. 浙江理工大学 材料与纺织学院、丝绸学院， 浙江 杭州 310018)

作为国家非物质文化遗产之一，中国蓝印花布是具有浓郁民族特色的纺织品。由于传统工艺的特点，蓝印花布纹样总是以或断或续的点和短线构成[1]，其独特的艺术形式深刻地反映出中国传统思想和美学观念。已有大量文献探讨传统蓝印花布纹样的文化与艺术内涵，但对于蓝印花布纹样的创新或未来则鲜有涉及。尽管可以提取纹样元素，利用某些平面设计软件进行再组合[2]，但这并不体现设计方法或模型。在纺织纹样生成技术方面，已有的研究方法主要是依靠一些数学模型的可视化，典型的研究，如利用Mandelbrot 集变换的印花图案设计[3]、L系统用于针织花型的设计[4]、弱混沌系统用于喷墨印花图案的设计[5]等。此类方法得到的纹样虽造型独特；但具有很大的随机性，难以保留原纹样的特征，因此并不适用于蓝印花布纹样或其他经典纹样的创新设计。

本文研究探索蓝印花布纹样的数学模型，使用数学模型进行纹样的匹配和重构，实现纹样的参数化，对参数化的纹样进行函数映射和骨架重组，达到纹样改造和创新设计的目的。本文提出的蓝印花布纹样的建模、重构和改造方法，可在保留蓝印花布纹样关键特征的同时，为蓝印花布纹样注入新的活力，以期在传统纹样的传承和创新中发挥积极作用。

1 研究方法

本文研究所使用的纹样来自一个蓝印花布纹样库[6]，包含各种经典蓝印花布纹样，可作为中国传统蓝印花布纹样的代表。典型纹样(局部)如图1所示。

图1 蓝印花布纹样示例Fig.1 Sample of blue calico pattern

传统工艺的特点决定了蓝印花布纹样在基本元素构成上，总是以各种形态的分离的点或短线呈现，通过点的大小、形态与疏密的变化达到纹样造型的多样性。此外，如受中国传统哲学中关于阴阳平衡的影响，传统蓝印花布纹样在基本元素构形上讲求“刚柔并用”“凹凸互补”，通过对立统一达到和谐的效果，因此，建模的重要目标，除了表达纹样元素丰富多样的形状，还要实现在刚与柔、凹与凸之间自由调节的能力。

1.1 模 型

1.1.1张力系数

给定4个控制点P0,P1,P2,P3，基数样条C由以下公式[7]确定：

C=m1h3(a)+P1h1(a)+P2h2(a)+m2h4(a)

(1)

式中：a为插值参数；h1,h2,h3,h4为经典三次Hermite多项式，分别为：

(2)

基数样条曲线以P1,P2为端点；m1,m2分别为曲线在点P1,P2处的正切值。

(3)

t即为张力系数，0≤t≤3。由式(3)可知：曲线在P1处的斜率由P0,P2,t决定；在P2处的斜率由P1,P3,t决定。图2示出张力系数对曲线外观的影响。

图2 张力系数对样条曲线的影响Fig.2 Influence of tension coefficient on spline

可见，利用张力系数能够实现样条曲线刚柔性的调节：张力系数值越大，曲线越柔和；反之则越刚硬；当t=0时，样条退化为直线。为得到封闭的形状，需将若干条样条曲线首尾相接。对于P0,P1,P2,P34个节点的情况，可由如下顺序确定4条基数样条曲线：(P0,P1,P2,P3)、(P1,P2,P3,P0)、(P2,P3,P0,P1)、(P3,P0,P1,P2)，如图3所示。

图3 由基数样条构成的封闭图形Fig.3 Closed figuires composed of cardinal splines

这4条曲线首尾相连构成封闭形状，且由基数样条的关于端点处斜率的性质可知，在每个节点处连接平滑。通过调整张力系数，图3中图形实现了从圆纹到方纹的转变。

1.1.2节点配置

将图3所示图形置于直角坐标系中，并进一步规定：P0,P1为活动节点，P2,P3为固定节点，如图4所示。P2,P3位于坐标轴上，其坐标分别为(-1,0)和(0,1)。活动节点P0,P1则可在一定范围内偏离坐标轴，其具体位置由活动半径(r0,r1)和偏离角(d0,d1)决定。由此构成的图形作为纹样元素的一般模型。

图4 元素模型Fig.4 Element model

该模型具有t,r0,d0,r1,d1共5个构形参数，其中t为样条曲线的张力系数。各个参数的取值范围规定如下：

(4)

对活动半径r0,r1取值范围的限制是为了避免出现长条形实例(蓝印花布纹样元素应当避免的形状)。对偏移角d0,d1(顺时针为正，逆时针为负)取值范围的限定，是为了将2个活动节点控制在各自的活动空间内，防止因交错导致形状畸变。张力系数t的取值范围由基数样条的性质决定。当这些参数值确定，模型形状即确定。由特定构形参数值确定的模型形状称为模型实例。模型实例经仿射变换(平移、缩放和旋转)即可匹配蓝印花布纹样中的元素形状，如图5所示。可见该模型对传统蓝印花布纹样中一些典型元素的表达能力。

图5 由模型实例表达的纹样元素Fig.5 Pattern elements expressed in model instances.(a)Shell; (b)Rice; (c)Petal

图5(a)所示为贝壳纹，模型参数为t=1.05,r0=1,d0=0,r1=0.5,d1=0；图5(b)所示为米粒纹，模型参数为t=0.3,r0=1,d0=0,r1=2.5,d1=0；图5(c)所示为花叶纹，模型参数为t=1.2,r0=2,d0=31.5,r1=3,d1=-40.5。实验结果表明，该模型可表现大量元素形状，包括刚柔性和凹凸性。当其中1个活动半径为负时，模型即表现凹形状。

1.2 重 构

纹样重建，即对纹样中的每个元素，选用合适的模型实例替代之，从而得到模型化的数字纹样。首先需要从蓝印花布纹样图像中提取纹样元素，然后从大量模型实例中找出与之最接近的，将该模型实例进行仿射变换应用到纹样空间以替代纹样元素。

1.2.1轮廓跟踪

轮廓跟踪法[8]可用来对二值图像中的目标进行轮廓提取。二值图像中存在目标和背景2类像素，通常目标像素(白色)值为1而背景像素(黑色)值为0。轮廓跟踪方法的步骤如下：

1) 按照从左到右、从上到下的顺序逐行扫描像素矩阵，直至发现第1个目标像素P，记下P点位置。

2) 设定P点的初始搜索方向为沿左下方，搜索方向每次逆时针累加旋转45°，直至找到第2个边界点Q，记下Q点的位置。

3) 将当前搜索方向顺时针旋转90°，作为Q点的初始搜索方向，搜索方向每次逆时针累加旋转45°，直至找到下一个边界点，令该点为新的Q点，记下位置。

4) 重复步骤3)，直至回到最初的P点。

图6为轮廓跟踪示意图。其中：空心圆点Q1～Q13表示搜索到的各个边界点；在每个边界点上，实线箭头表示初始搜索方向。

图6 轮廓跟踪原理图Fig.6 Schematic of contour tracing

以蓝印花布扫描图像为原始素材，在进行轮廓跟踪提取纹样元素前，需要进行一些必要的预处理，主要步骤如图7所示。

图7 元素提取的步骤Fig.7 Procedures of element extraction. (a) Original image (grayed); (b) Median filtering; (c)Threshold segmentation; (d)Contour tracing

原始图像经灰度化后，先通过中值滤波[9]去除噪声；再使用OTSU算法[10]进行阈值分割，分离出目标与背景；最后，使用轮廓跟踪算法提取图像中每个纹样元素的矢量轮廓。

1.2.2模型实例选取

图像的Hu矩对应了一系列图像，这些图像可由其中任何一个平移、缩放和旋转得到。换言之，Hu具有平移、缩放和旋转不变性[11]。对于数字图像f(x,y)，其p+q阶标准矩mpq定义为

(5)

其中，N和M分别是图像的高度和宽度。数字图像的p+q阶中心矩μpq定义为

(6)

(7)

图像的Hu矩是基于归一化中心矩jpq的1组不变矩，它由7个特征值(M1～M7)组成：

(8)

形状是图像的特例，形状f(x,y)的值域只有2个可能：0或1。当点(x,y)在形状轮廓线上时，值为1；否则为0。本文研究涉及的模型形状和元素形状，均可转换为数字图像，从而利用Hu矩的不变性。进行实例选取时，先计算纹样元素的Hu矩，然后比对元素形状与每个模型实例的接近程度(2个Hu矩的欧式距离)，找出最接近的模型实例，结果如图8(b)所示。其模型参数为t=1.2,r0=0.5,d0=0,r1=1,d1=0。

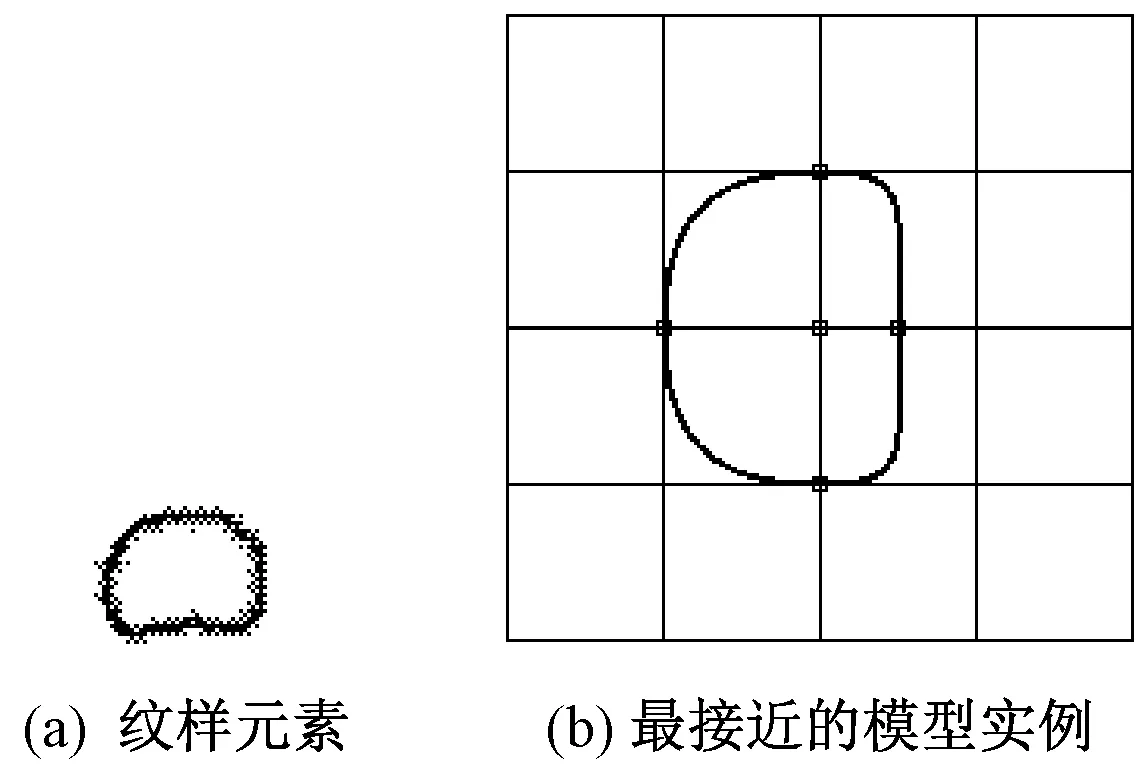
图8 基于Hu矩的模型实例选取Fig.8 Instance selection based on Hu moments.(a) Pattern element; (b) slosest model instance

1.2.3模型实例变换

最接近(或对称)实例与元素形状相似度最高，需要对其进行仿射变换(平移、缩放和旋转)，使之尽量与元素形状重合，以替代纹样元素。考虑到形状重合的2个必要条件：形状几何重心一致；形状面积相等。

图9 实例变换过程Fig.9 Procedures of instance transform

其次，计算二者面积之差，若大于零(模型实例面积大于元素面积)则将模型形状逐步缩小，否则逐步放大，直到二者面积相等，此时的缩放率记为s。

最后，将模型实例在0°～360°上旋转，计算每个角度上模型实例与纹样元素的重合度，记取重合度最大的角度θ。

图10 重构的纹样Fig.10 Reconstructed pattern

1.2.4映射函数

对模型匹配后的数字化纹样，使用映射函数将模型参数映射到新的区间，实现纹样创新。参与映射的可以是构形参数，也可以是仿射参数。图11示出对数字化纹样进行重构的图例。

图11 通过映射函数进行的纹样改造Fig.11 Modifications by mapping functions. (a) Mapping of tension coefficient; (b) Mapping with conditions

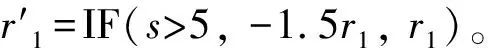
2 结果与讨论

2.1 泛化的模型

本文研究提出的模型使用4个节点，按特定的顺序定义4条首尾相连、平滑过渡的基数样条曲线，形成封闭形状。利用张力系数表现形状的刚柔性，通过定义活动节点实现了形状的凹凸性和多样性。实验结果证明，该模型能够很好地表现大多数传统蓝印花布纹样元素。但仍有一些纹样元素超出了其能够表达的范围，特别是那些由于不便在传统工艺下印制而在实践中较少采用的元素[2]。这些元素超出了4节点样条曲线所能表现的范围，如图12所示。表现这样的元素形状需要更多节点和更复杂的模型，这种模型可由上述4节点模型泛化而来。

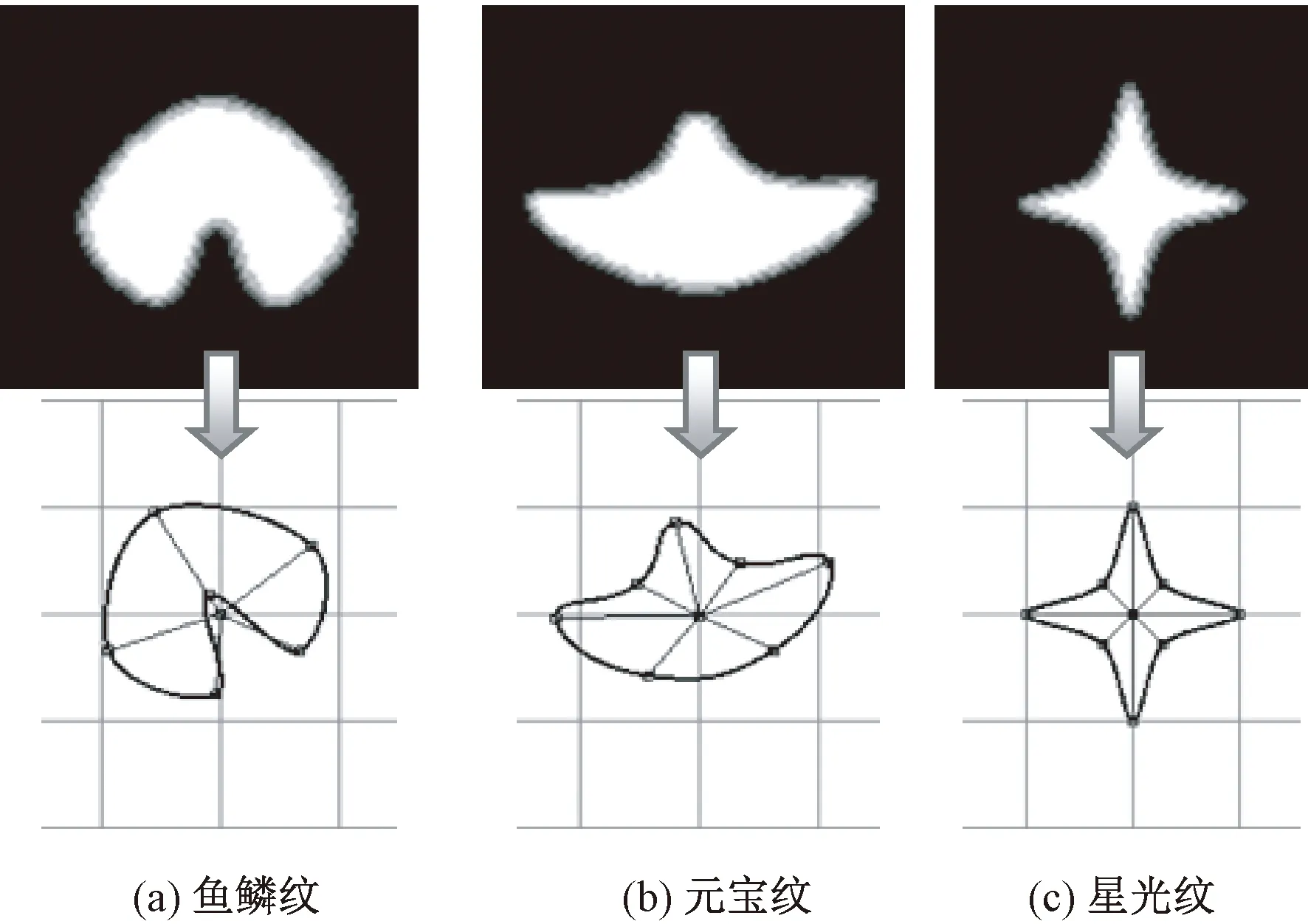
图12 利用泛化模型表达复杂元素Fig.12 Complex elements expressed in generalized model.(a)Scale pattern; (b)Treasure pattern; (c)Starlight pattern

图12(a)为鱼鳞纹，模型参数为t=0.9,r0=0.75,d0=27,r1=-0.2,d1=0,r2=0.75,d2=-27,r3=1,d3=-20,r4=1.1,d4=0,r5=1,d5=20；图12(b)为元宝纹，模型参数为t=0.7,r0=1.2,d0=-25,r1=0.7,d1=-25,r2=0.7,d2=25,r3=1.2,d3=25,r4=0.6,d4=5,r5=0.9,d5=0,r6=0.6,d6=-5；图12(c)为星光纹，模型参数为t=0.8,r0=1,d0=0,r1=0.4,d1=0,r2=1,d2=0,r3=0.4,d3=0,r4=1,d4=0,r5=0.4,d5=0,r6=1,d6=0,r7=0.4,d7=0。

设有n(n≥4)个节点(记为P0,P1,P2，…，Pn-1)，以顺时针方向分布于单位圆(半径为1)的圆周等分点上，2个相邻节点之间的圆心角为(360/n)°，点O为圆心或参考点，如图13(a)所示。

图13 泛化模型Fig.13 Generalized model. (a)Number of knots; (b)Range of activity

规定每个节点可以偏离所在的等分点，其坐标位置由活动半径ri(-10≤ri≤10)和偏离角di(-180/n≤di≤180/n)决定，如图13(b)所示。使用基数样条，按如下顺序连接所有节点以构成封闭形状：(P0,P1,P2,P3),(P1,P2,P3,P4)，…，(Pn-1,P0,P1,P2)。当n=4且固定节点P2,P3时，即为本研究中所使用的4节点模型。

此泛化模型中，每个节点对应2个参数(活动半径和偏移角)，另外加上张力系数，模型中的参数个数为2n+1，模型实例的数量为m2n+1(m为取样次数)。只要节点数量足够多，模型就可以表达复杂纹样元素。使用6节点、7节点及8节点模型表现复杂元素，如图12所示。但节点增加，意味着模型参数的增加，造成重构过程运算量大幅上升。实际应用中可根据纹样元素的复杂程度决定n的取值。

2.2 作为骨架的模型

目前为止，本文研究提出的模型是针对纹样元素的，但实际上它也可以作为纹样的骨架，进而实现更高层次上的建模。总体来说，蓝印花布纹样主要呈现2种基本的骨架，即环形骨架和线形骨架，如图14中虚线所示。

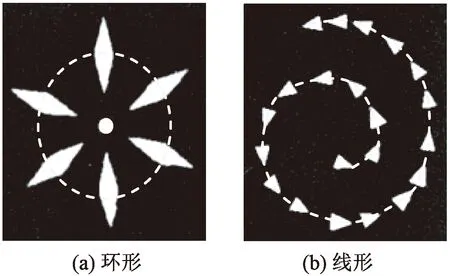
图14 2种基本骨架Fig.14 Two basic skeletons. (a) Circular; (b) Threaded

在环形骨架中，骨架线上的纹样元素围绕一个中心点分布，该点称为骨架中心；而在线形骨架中，纹样元素根据骨架线的切线方向分布。需要注意的是，环形骨架的骨架线不一定是圆形，可以是任何闭合的形状。大多数复杂的纹样都可分解为这2种骨架的组合。

若以图15所示的圆纹作为纹样骨架，构成骨架的点集(xi,yi)可由式(1)中模型的样条定义取得。其中：i=0,1,2，…,k-1；k是骨架线上的总点数。

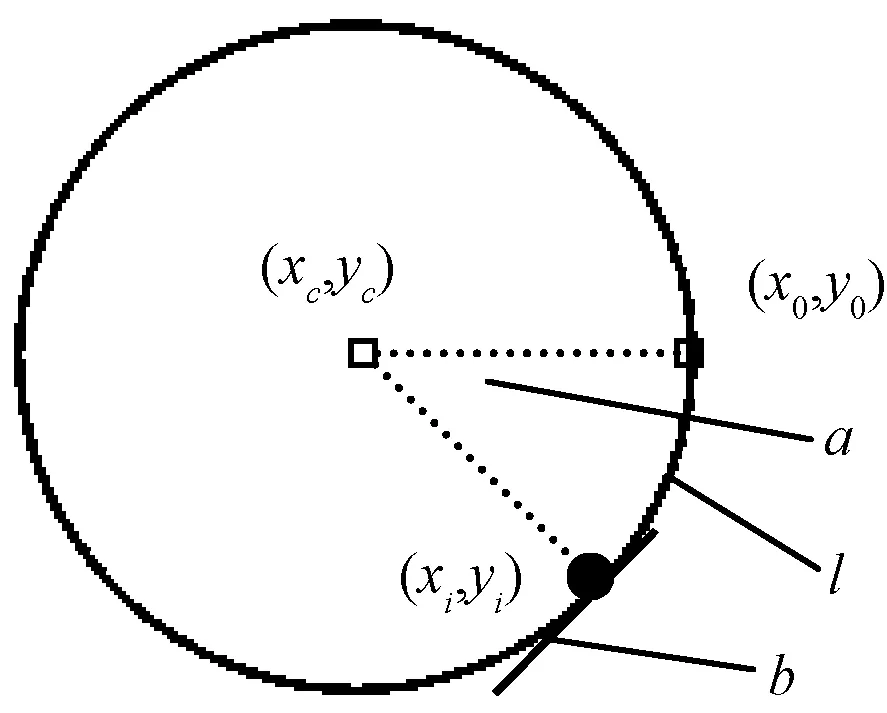
图15 作为骨架的模型Fig.15 Model as skeleton

点(x0,y0)是骨架的起点，模型的原点(xc,yc)可作为骨架的中心点(在线性骨架中，该点可以忽略)。骨架上的每个点(xi,yi)拥有3个属性，即中心角(以a表示)、切线角(以b表示)和步长(以l表示)。中心角是骨架起点、中心点及当前点构成的角度；切线角是当前点在骨架线上的切角；步长是沿骨架线从起点到当前点的路径长度。这3个属性可通过下式计算：

(9)

(10)

(11)

另外，骨架线的总长度(以L表示)为

(12)

沿骨架线进行纹样元素的分布，称为骨架的具化。上述3个属性将对骨架的具化产生影响。在实施骨架具化前，构造1个种子元素(由5个构形参数和4个仿射参数决定)，1个定位器函数(Dp)和1个定形器函数(De)。定位器根据步长决定是否放置元素，在放置元素时定形器负责对种子元素实施调整，即根据当前中心角或切线角对种子元素的构形参数和仿射参数进行调整，实现骨架线上纹样元素的变化。骨架具化的例子如图16所示。

在图16 (a)中，以方纹为骨架，用柱状纹作为种子元素对其进行具化。定位器沿骨架路径每隔L/8放置纹样元素，定形器将元素的旋转角θ(元素模型的仿射参数之一)设置为骨架中心角a的线性函数，从而实现了环形骨架。图16(b)中的定形器在图16(a)基础上增加了对张力系数t的控制，通过将当前值设为对最近一次张力系数值(tprev)递增，实现骨架上纹样元素刚柔性的渐变。图16(a)、(b)的骨架具化函数如下：

图16 (c)、(d)中的纹样都以贝壳纹作为骨架、以米粒纹作为种子元素。二者的区别在于，前者的定形器以中心角a作为参数产生了环形骨架，而后者的定形器以切线角b作为参数产生了线形骨架。可见，骨架具化过程中产生环形或线形骨架，取决于定形器使用中心角还是切线角作为参数。图16(c)、(d)的具化函数如下：

图16(e)、(f)中，都使用定形器产生环形骨架，同时对元素的缩放率s进行调整，通过将当前值设为对最近一次缩放率(sprev)的倍数，带来了骨架线上元素尺寸的渐变。图16(f)中的定位器引入了非线性函数，因此与图16(e)相比，骨架线上元素间的间隔不是均匀的而是递增的。图16 (e)、(f)的具化函数如下：

上述实例展示了作为骨架的模型对2种基本骨架的模拟，以及通过模型参数变化带来的创新。其中元素的渐变和非线性分布是对传统蓝印花布纹样的创新性改造。

3 结 论

本文研究基于基数样条曲线对蓝印花布纹样元素建模，利用张力系数表达形状的刚柔性，通过配置活动节点实现形状的凹凸性和多样性。对于一些超出4节点模型表达范围的形状，可通过泛化模型覆盖。在纹样重构方面，先使用轮廓跟踪技术从图像中提取纹样元素，然后利用Hu矩的不变性选取与之最接近的模型实例，再利用矢量形状的重心、面积及重合度对模型实例进行仿射变换，将其应用到纹样空间，完成纹样数字化。对数字化纹样，通过映射函数调节模型参数进行纹样元素的改造和创新。对于拥有闭合骨架的纹样，通过将元素模型应用到骨架进行纹样骨架的改造，再利用定位器和定形器实施骨架具化，完成更为深刻的改造。实验结果证明，本文模型及其泛化版本可以很好地表现绝大多数蓝印花布纹样元素，该模型用于纹样骨架也可带来丰富的创新效果。

FZXB