具有S-型分布时滞和反应扩散的非自治神经网络的全局指数稳定性和有界性分析

李 宾 ，龙述君

（1.西华大学理学院，成都610000；2.乐山师范学院数学与信息科学学院，四川乐山614004）

近年来，各种各样的神经网络模型得到了广泛的研究并被成功应用于图像处理、信号处理、模式分类、模式识别、最优化问题等领域.在神经网络的实现过程中，时滞现象经常发生，这可能会使系统出现混沌、震荡和不稳定等现象.因此，在神经网络系统带入时滞是有必要的.相关学者对含有时滞的神经网络进行了深入研究[1-8].通常情况下，既含有离散时滞又含有分布时滞的神经网络系统不易处理，而在实际应用中，这种情况又不可避免.文献[9]首次提出了S-型分布时滞，统一了离散时滞和分布时滞，自此，含有S-型分布时滞的神经网络成为研究热点[10-16].在神经网络系统中，当电荷在不对称的电磁场中运动时，产生的反应扩散效应是不可忽略的.因此，含有反应扩散的神经网络也得到了广泛研究[17-19].众所周知，自治神经网络模型仅仅是对现实问题的一种简单表述，而非自治模型能更准确地描述实际问题.目前，对于含有S-型分布时滞和反应扩散的非自治神经网络的研究较少.本文考虑含有S-型分布时滞和反应扩散的非自治神经网络的全局指数稳定性和有界性，得到了系统全局指数稳定和有界的充分判定准则，所得结论是目前已有相关判定准则的拓展.

考虑如下具有S-型分布时滞和反应扩散的非自治神经网络模型

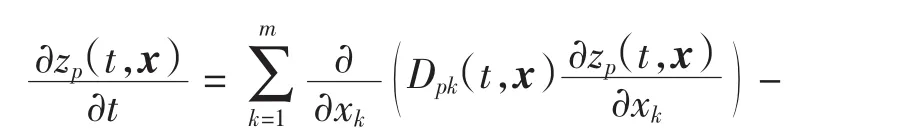
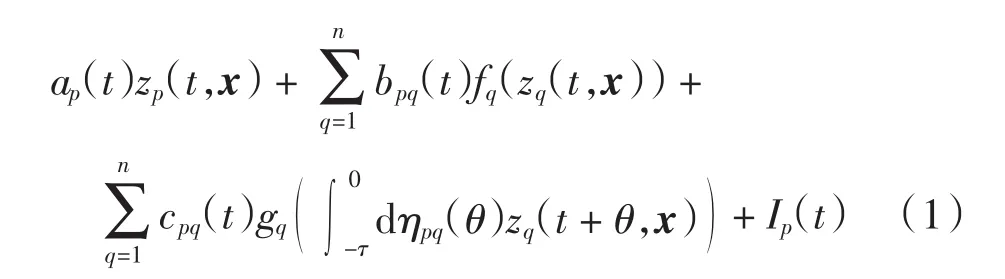
边界条件和初值条件分别为

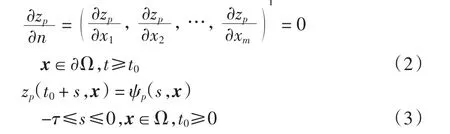
1 预备知识

令 N={1，2，3，…，n}， R+=[0，+∞）， Rm×n为 m × n阶实矩阵全体构成的集合，En×n（或E）表示n×n阶单位矩阵.D+φ（t）表示在 t时刻 φ（t）的右上导数.

对于一个非奇异 M-矩阵 D[1]， 记 ΩM（D）={z∈Rn|表示矩阵 Cn×m和 Dn×m的Hadamard积.L2（R+×Ω）表示 R+×Ω 上所有实Lebesgue可测函数全体构成的集合，且关于范数

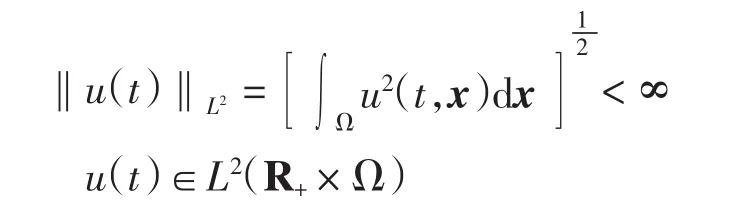
构成Banach空间.令

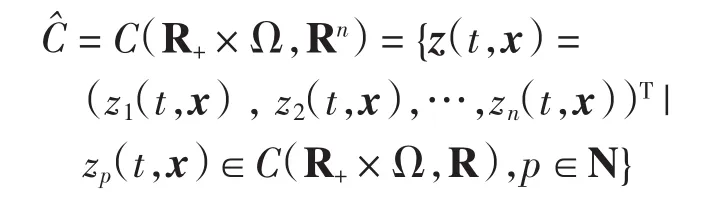
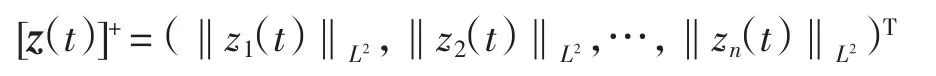
定义如果存在常数λ＞0和M≥1，使得对于系统（1）的任意 2个分别对应初值 φ（t）、φ（t）∈C 的解x（t；t0，φ）、y（t；t0，φ）， 均有

则称系统（1）是全局指数稳定的.其中

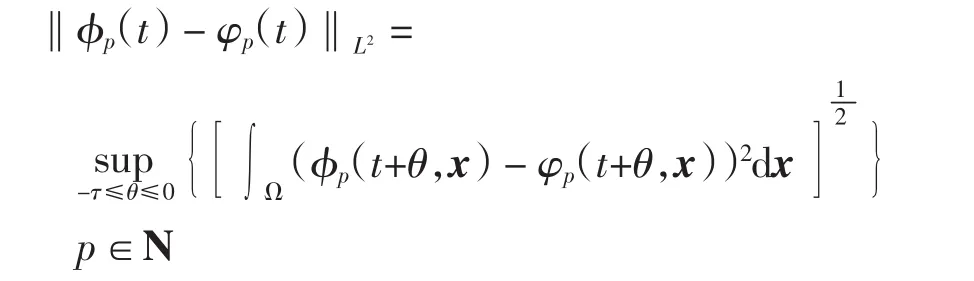
引理设x（t）∈C[R，Rn]满足如下微分-积分不等式

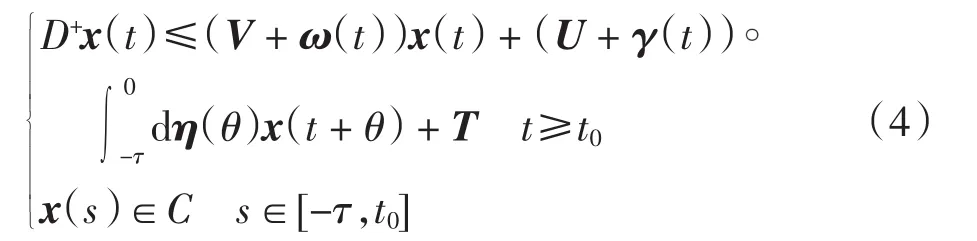
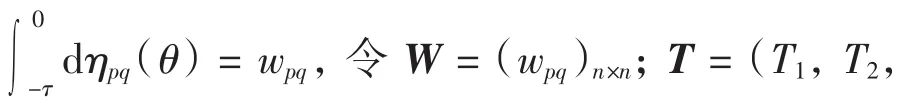
如果

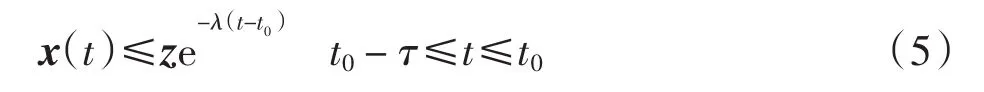
则 t≥t0时，

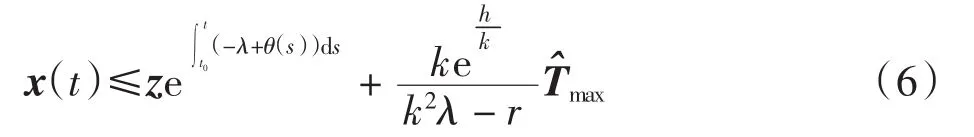
其中：λ ＞ 0，z∈ΩM（Π）满足

且存在常数 r∈（0，k2λ）和 h≥0， 使得对任意 t、v∈[t0，+∞）有

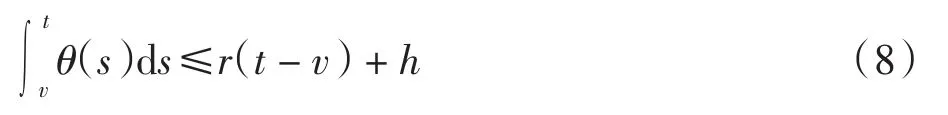
证明由Π是一个M-矩阵，则存在一个正向量z∈ΩM（Π）使得 Πz＞0，即（V+UW）z＜0.由连续性知，存在一个常数λ＞0，使得式（7）成立.

首先证明当 t∈[t0， +∞）时， 有

其中 n（s）=-kλ + θ（s）/k.为此， 首先验证对任意 ε ＞1，有

假设式（10）不成立， 由式（5）和当 t≥t0时 x（t）的连续性知，存在一个t*＞t0和m∈N，使得

其中 p∈N 且 p≠m.结合式（4）中 U=（upq）n×n≥0 和vpq≥0（p≠q）可得

显然式（13）与式（11）的第2个不等式矛盾，因而式（10）成立.在式（10）中，令 ε→1+，则有式（9）成立.

结合式（8）和式（9）可得

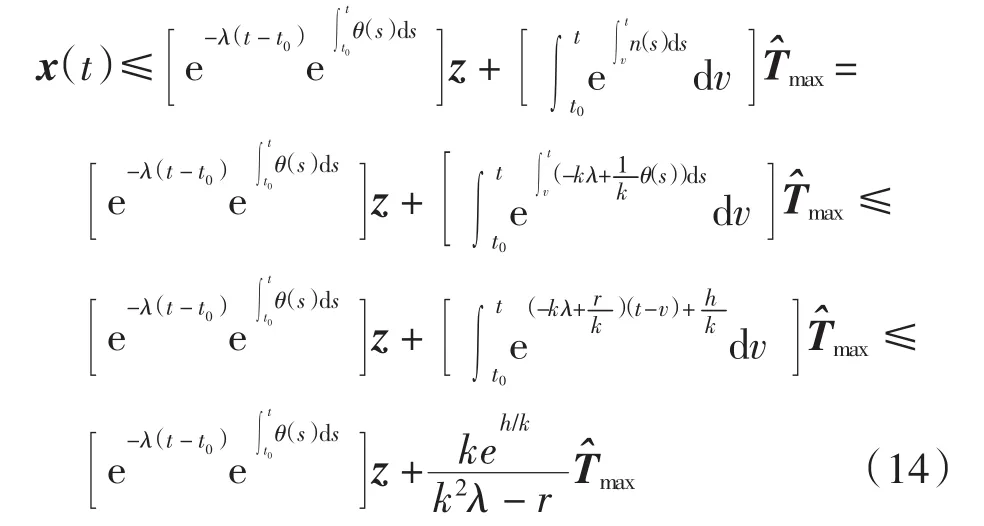
证毕.

注1在引理中，当n=1时，令w11=1，T=0，ω11（t）≡0，γ11（t）≡0，t≥t0，则通过简单推证可得文献[10]的引理2.

注2在引理中， 若 wpq=1（p、q∈N），ω（t）≡ 0，γ（t）≡ 0， t≥t0， 则通过简单推证可得文献[19]的引理5（b=k（1，1，…，1）T，k∈R）.

2 主要结果

对系统（1）做如下假设：

（A1）对任意p、q∈N，ap（t）＞0，bpq（t）、cpq（t）、Ip（t）为定义在[t0，+∞）上的有界连续函数.

（A2）对任意q∈N，存在正常数lq和kq，使得

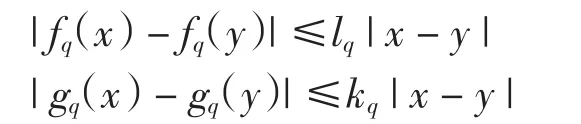
（A3）在区间[t0，+∞）上，存在非负可积矩阵函数， 使得

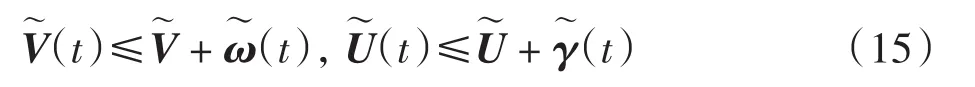
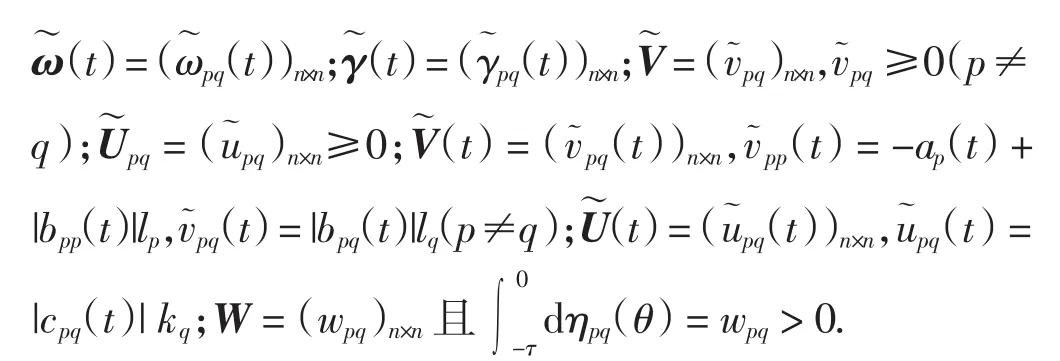
（A4）集合非空， 存在正向量和常数满足

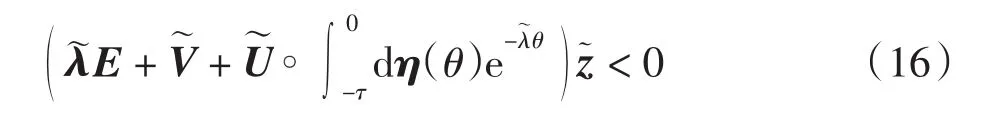
（A5）存在常数， 使得

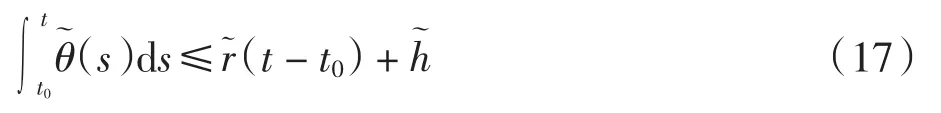
其中

定理1设条件（A1）～（A5）成立， 则系统（1）是全局指数稳定的且指数收敛率不小于

证明设u（t，x）=（u1（t，x），u2（t，x），…，un（t，x））T、v（t，x）=（v1（t，x），v2（t，x），…，vn（t，x））T是系统（1）的2个分别满足初值的解，则

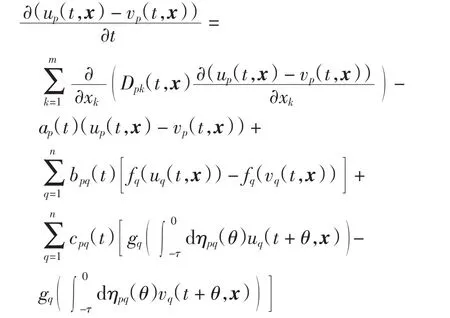
令ep（t，x）=up（t，x）-vp（t，x）（p∈N），可得

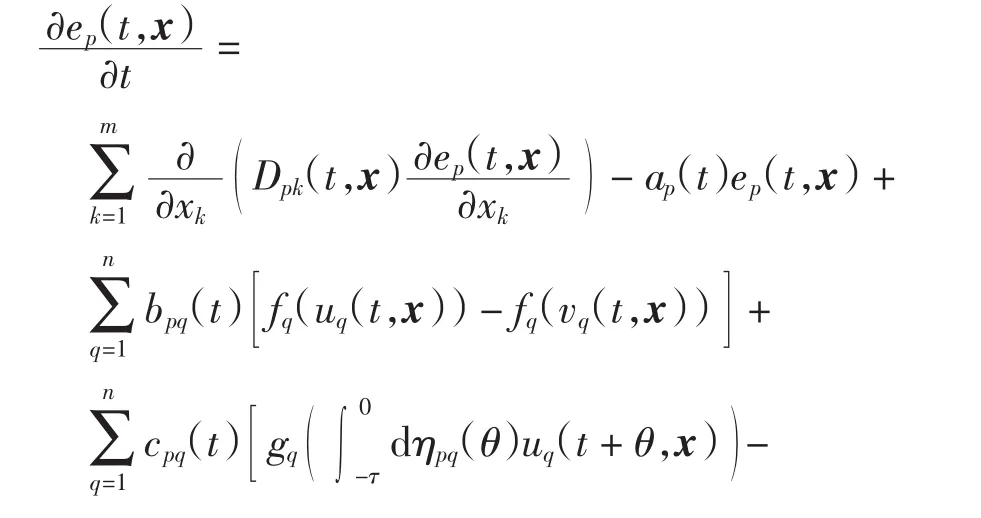
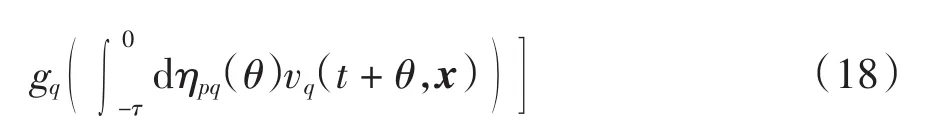
对式（18）两边同时左乘ep（t，x）并在Ω上对x积分，得到

由式（2），得到

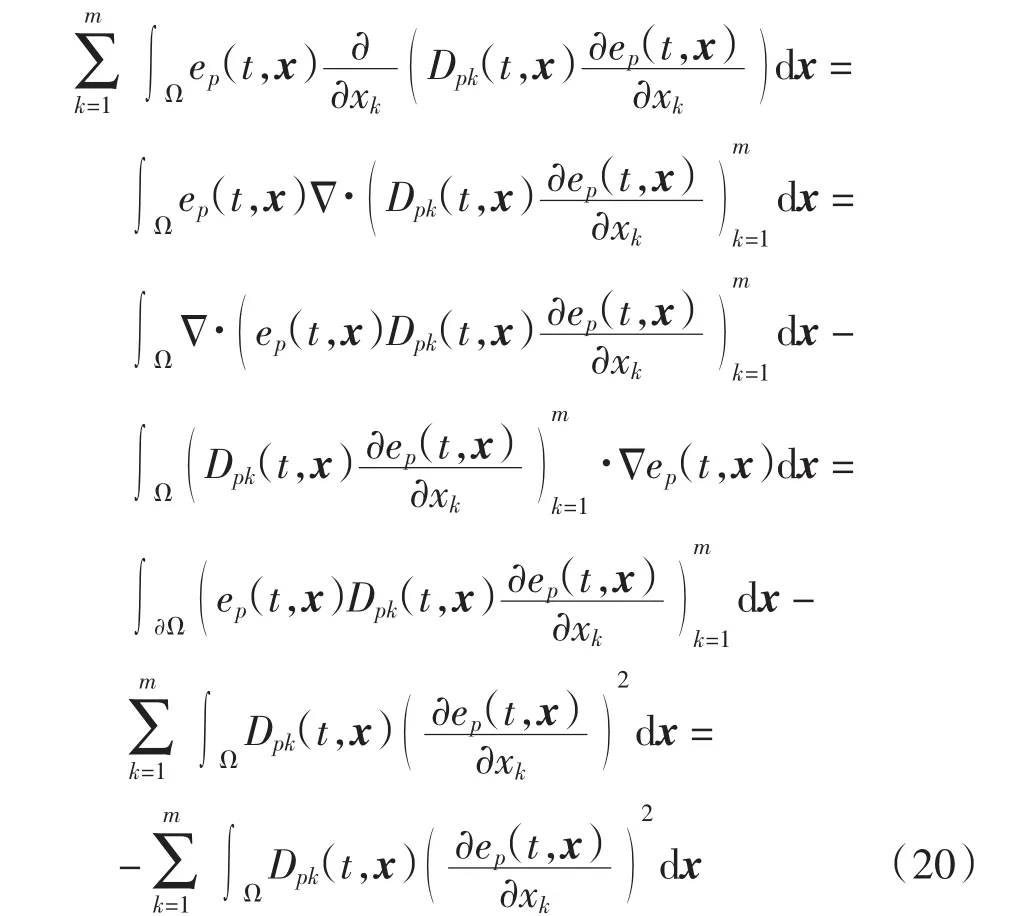
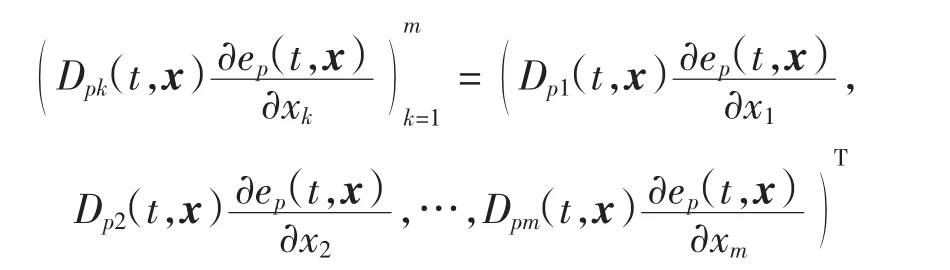
结合式（19）和式（20）、条件（A2）及 Cauchy-Schwarz不等式，得到

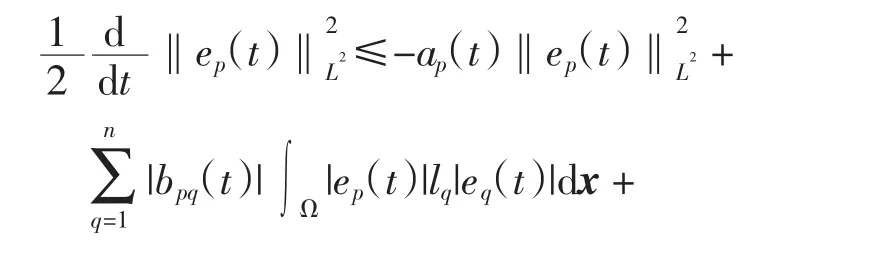
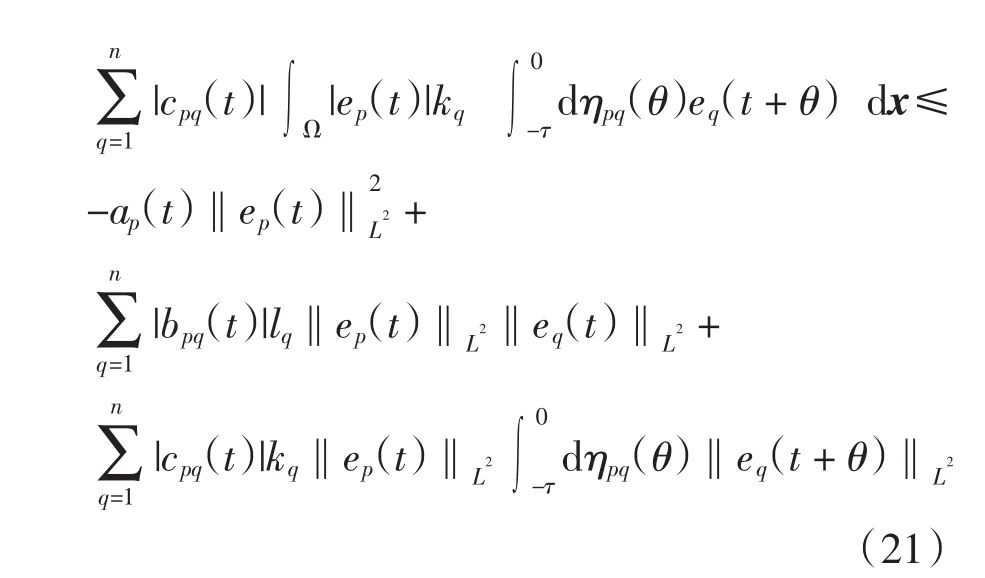
结合式（21）和条件（A3）有

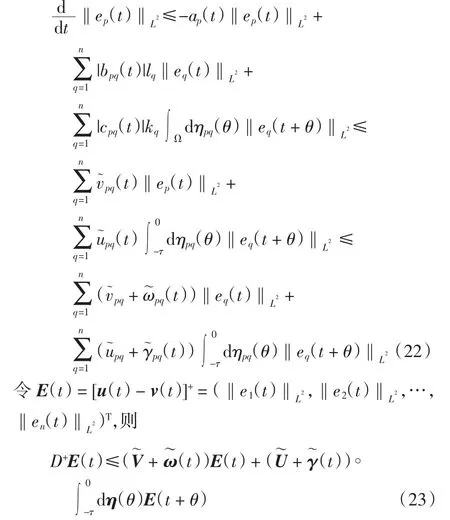
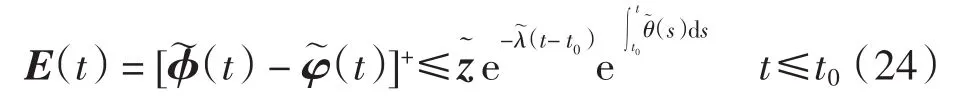
由式（23）和式（24），并在引理中令T=0，得到

由式（17）和式（25）得到

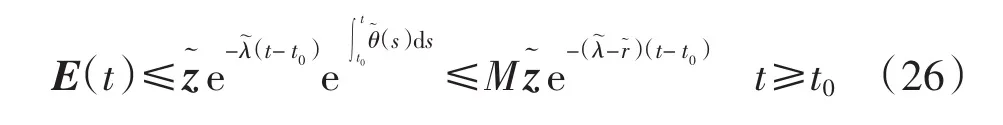
注3若系统（1）是自治系统，即ap（t）≡ap＞0，bpq（t）≡bpq，cpq（t）≡cpq，Ip（t）≡Ip，由条件（A2）可推出自治系统存在唯一的平衡点，通过简单推证可得文献[17]的Theorem1.

定理2设条件（A1）～（A5）成立， 则系统（1）的所有解都是有界的.

证明设u（t，x）=（u1（t，x），u2（t，x），…，un（t，x））T是系统（1）的满足初始条件的解， 则

在式（27）两边左乘up（t，x）并积分，得到

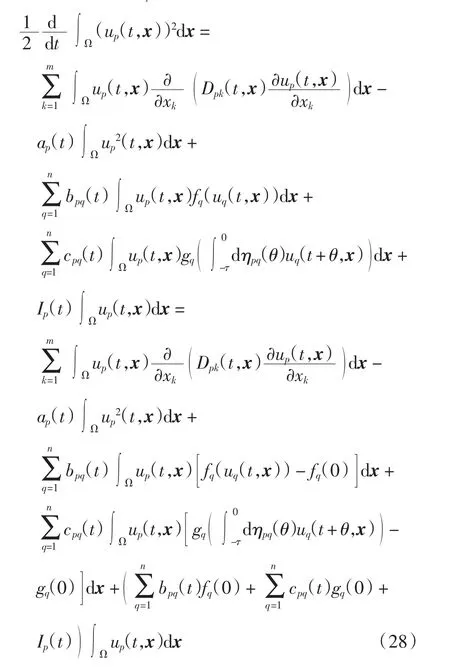
用与式（20）类似的推导方法可得

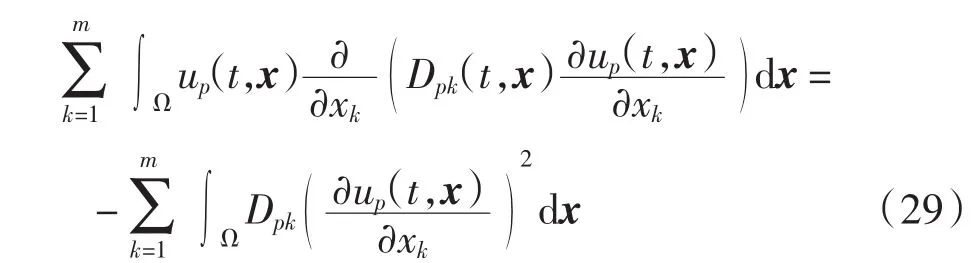
结合式（28）和式（29），条件（A2）及 Cauchy-Schwarz不等式，得到

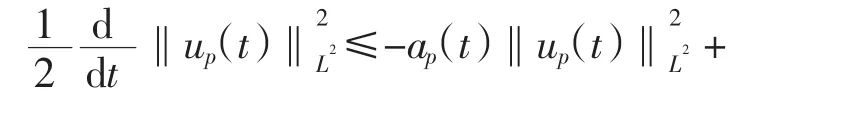
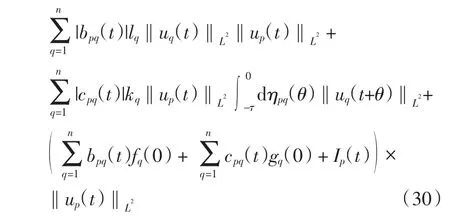
由式（30）、条件（A1）和条件（A3）， 有

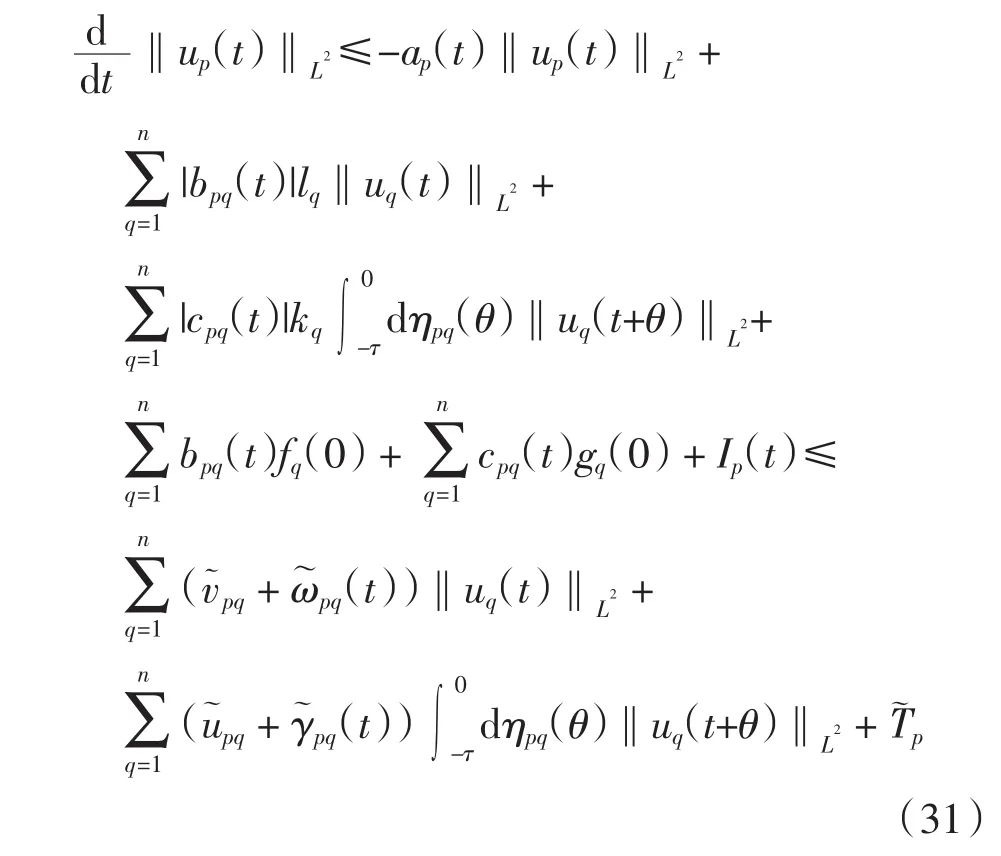
利用向量放缩得

由式（17）、式（32）、式（33）和引理可得

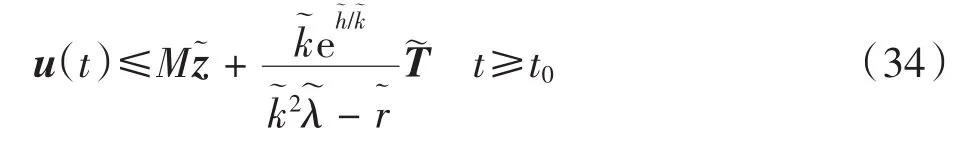
3 算例与数值仿真

例考虑模型（1）具有如下系数

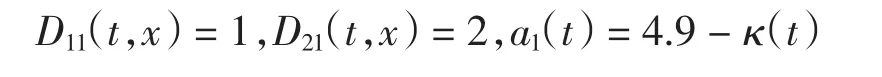
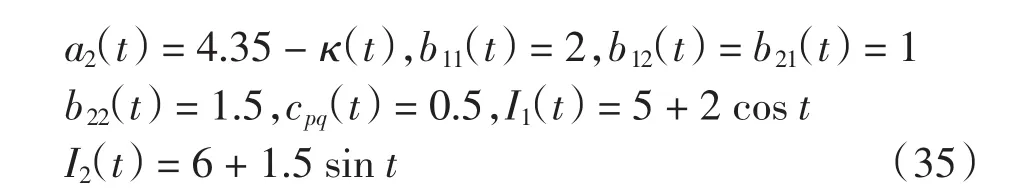
进而得到

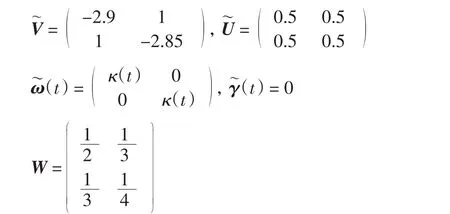
通过简单计算得

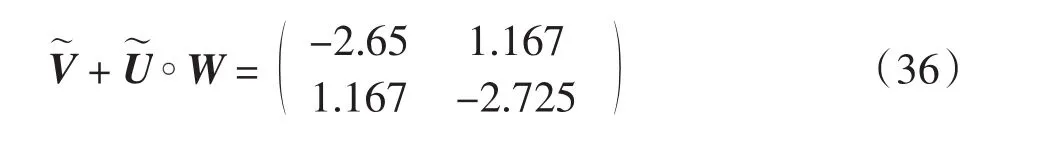
由文献[20]得

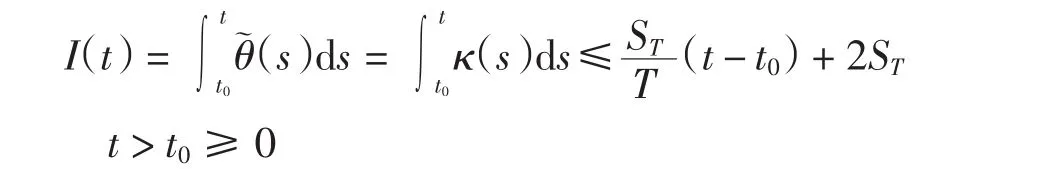
特别地，当m∈N时，令

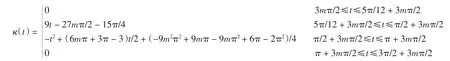
图1 ‖u（t） -v（t）‖L2的衰减曲线Fig.1 Attenuation curve of‖u（t）-v（t）‖L2

图2 u1（t）和x的状态曲线Fig.2State trajectory of u1（t）and x

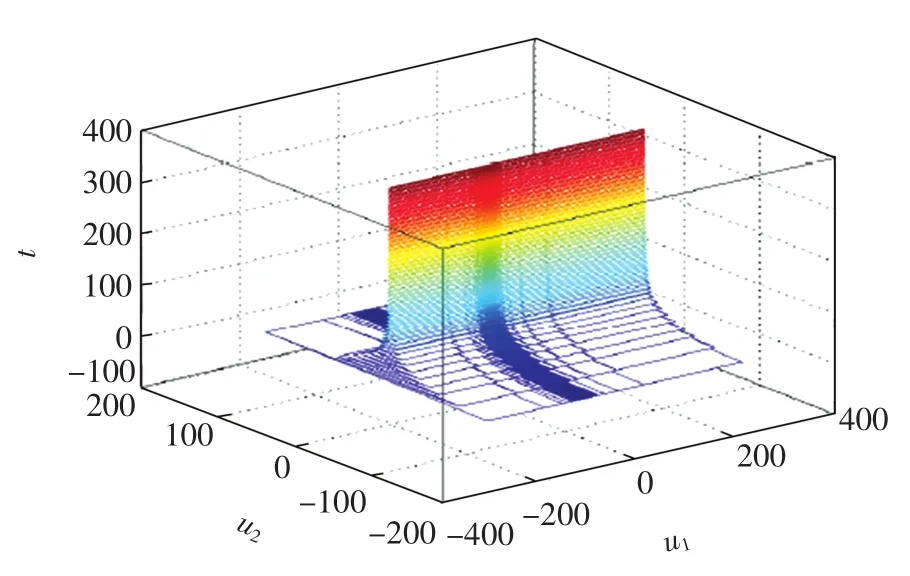
图3 u1（t）和u2（t）的状态曲线Fig.3State trajectory of u1（t）and u2（t）

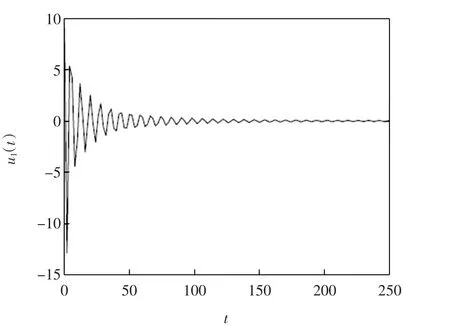
图4 u1（t）对应的图形Fig.4Curve of u1（t）

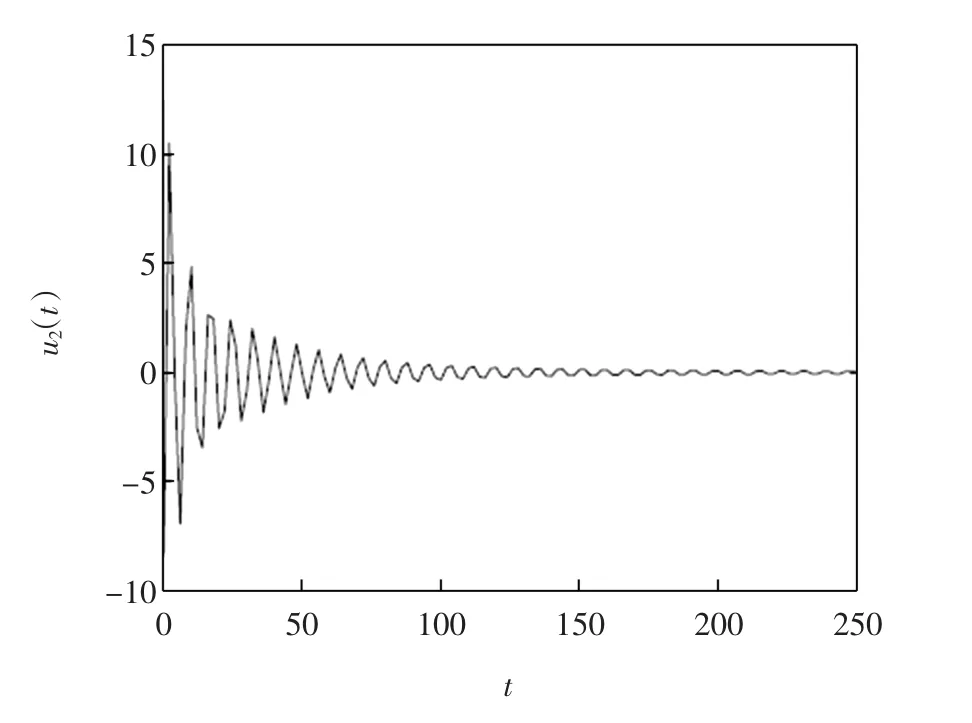
图5 u2（t）对应的图形Fig.5Curve of u2（t）

而在算例系统中， 令 d=（1，1）T， 得到

图6 J1（t）和J2（t）的图像Fig.6Curves of J1（t）and J2（t）

由图6知，J1（t）＜0，J2（t）＜0均不成立，因此，文献[21-22]的判别准则对本文系统是失效的.