风险投资机构与创业企业双边匹配决策研究

邱 科

（重庆工商大学 财政金融学院， 重庆 南岸400067）

一、前言

风险投资不但有助于创业企业规模的不断扩大， 同时也有助于创业企业研发创新等各项成长能力的提升，有效促进企业竞争优势，帮助创业企业做大做强［1］。 成功的风险投资不仅能带来资本的增值，同时还获得声誉收益［2］。所以风险投资与创业企业的合理、稳定及有效匹配是至关重要的，是一个值得研究的课题。

匹配决策起源于大学录取和婚姻配对问题［3］，随后大量学者开始涌入匹配领域进行研究。Roth 在婚姻匹配研究的基础上，结合实际需要，将匹配理论应用于住院医生配对项目（NRMP）的场景当中［4］，之后由于NRMP 参与人数下降，Roth 又扩展了G-S 算法，提出H-R 算法［5］。 为了得到更加稳定合理的匹配结果，解决H-R 算法中的单边占优问题，李铭洋等提出了将双方主体匹配序值之和取最小作为目标构建了多目标优化模型［6］，王彦博等提出了WYS 算法［7］，他们从计算方法方面完善了双边匹配理论。 由于双边匹配理论有着广泛的应用前景，众多学者将其应用于各个领域当中，例如实习医师与医院的匹配研究［4］，人力资源管理中的人岗匹配问题［8-9］，电子商务环境下买方与卖方的匹配问题［10-11］。

上述文献为双边匹配理论在金融市场设计领域的应用提供了理论基础和研究方法支撑，近年来，学者开始了这方面的应用研究。 曹国华等利用文献［3］中的匹配算法，建立了风险投资家与创业者的双边匹配模型并探讨了双方之间的双向选择关系［12］；万树平等构建了具有不同类型信息的风险投资商与投资企业双向选择的多指标评价匹配模型, 给出了一种多指标双边匹配决策方法［13］；吴凤平等针对互联网金融背景下风险投资双边匹配的选择问题，构建了相应的匹配决策模型［14］。 这些文献为双边理论在金融市场设计方面的应用做出了重大贡献。但需要指出的是，在风险投资机构与创业企业的匹配问题中，由于金融市场信息存在复杂性和不确定性，匹配主体的需求信息是多层次、多类型的［15］。 例如，风险投资机构为了找到优质的创业企业可能设计管理团队、技术与产品、市场与竞争环境等多重评价指标，而这些指标会用得分评价或语言短语等不同方式来表达。 鉴于此，本文针对风险投资机构与创业企业需求信息的多元化，依据前景理论构建考虑双方心理行为的双边匹配模型，并用实例验证模型的实用性和有效性。

二、风险投资机构与创业企业的双边匹配描述

文中相关的数据类型定义：S={S0，S1，S2，…，Sn}，S 为有序短语集，且n 为偶数，Sθ（θ=0，1，2，…，n)为第θ 个短语；={Sθ1，Sθ1+1，…，Sθ2}≜［Sθ1，Sθ2］，其中Sθ1，Sθ2∈S，且0≤θ1≤θ2≤n，S 是短语集，则称为离散区间语言变量；T={T1，T2，T3，…，Tn}，T 为离散得分集，若α＞β，则Tα＞Tβ；Tk={Tk1,Tk1+1，…，Tk2}≜［Tk1，Tk2］，其中Tk1，Tk2∈T，且1≤k1≤k2≤n，T 是离散得分集，则称Tk为离散区间得分变量。

风险投资市场存在三方主体，即风险投资机构集合，定义为X={x1，x2，x3，…，xn}，其中xi（i=1，2，3，…，n)为第i 个风险投资机构；创业企业集合，定义为Y={y1，y2，y3，…，ym}，其中yj（j=1，2，3，…，m)为第j 个创业企业；另外一个为投资中介机构。 风险投资机构为资金的供给方，为创业企业提供资金而获取高额回报。 创业企业为资金的需求方，以取得资金而实现企业的快速发展。 投资中介根据双方的投融资需求进行匹配，其收益高低取决于匹配的成功度。

风险投资机构根据投资预期，对创业企业的各项发展指标提出要求，形成对创业企业需求的期望信息。 指标集定义为Ax={a1，a2，a3，…，an}，Ax为风险投资机构对创业企业n 个评价指标的集合，ai（i=1，2，3，…，n)为第i 个指标为对应于指标集Ax的权重向量为ai指标的权重，且满足归一化要求；期望集定义为

创业企业根据自身融资情况，对风险投资机构的各项资质提出要求，形成对风险投资机构需求的期望信息。指标集定义为By={b1，b2，b3，…，bm}，By为创业企业对风险投资机构的m 个评价指标的集合，bj（j=1，2，3，…，m)为第j 个指标；为对应于指标集By的权重向量为bj指标的权重，且满足归一化要求；期望集定义为为yj对xi针对By对应的期望集，其中为yj对xi针对bj指标的期望值，且

投资中介得到风险投资机构和创业企业双方反馈的需求期望信息， 然后对双方的实际情况进行评价。其中实际情况评价集定义为为中介对xi针对By对应的实际评价集，其中为中介对xi针对bi指标的实际评价值，且

风险投资机构与创业企业的双边匹配定义为：映射μ（X∪Y→X∪Y），对任意xi∈X，yj∈Y，满足μ（xi）∈Y， μ（yj）∈X∪{yj}，则称μ（xi）=yj， μ（yj）=xi为第i 个风险投资机构与第j 个创业企业在映射μ 中双边匹配，即（xi，yj）。 若（xi，yj）中， μ（xi）=yj≠yj′，yj′∈Y； μ（yj）=xi≠xi′，xi′∈X，则称第i 个风险投资机构xi与第j 个创业企业yj为一一匹配。若μ（yj）=yj，则称第j 个创业企业yj匹配失败，没有风险投资机构投资。

风险投资机构根据指标集Ax，针对不同类型指标ai给出不同类型的期望值。 创业企业根据指标集By，针对不同类型指标bi给出不同类型的期望值。投资中介通过实际调查，对xi和yi根据指标集Ax和By中的每一个指标进行实际评价。 所以本文根据风险投资机构和创业企业给出的不同类型需求的期望信息和投资中介调查得出的实际评价信息，通过一个有效的匹配方法获得最优匹配方案，从而获得合理有效的匹配结果。

三、风险投资机构与创业企业的匹配模型构建与求解

（一）损益值计算

以风险投资机构与创业企业需求信息的期望值作为参照点，利用不同的数据处理方法将投资中介的实际评价信息转化为相对于参照点的损益值。对于风险投资机构xi，其评价指标的期望值为，创业企业的实际评价值为对于创业企业yj，其评价指标的期望值为风险投资机构的实际评价值为

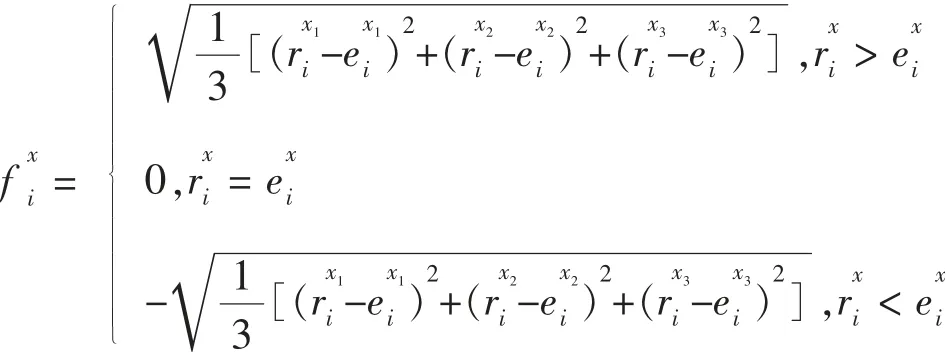
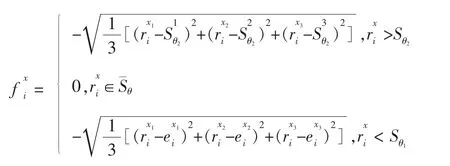
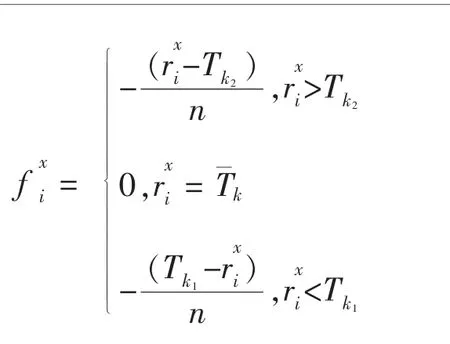
（二）前景值计算

考虑风险投资机构和创业企业在损失和收益情景下对待风险态度的不同，以及损失规避原则，分别计算其前景值。 设风险投资机构xi对创业企业yi前景值为V（），创业企业yi对风险投资机构xi的前景值为为xi对yi的单个指标损益值的前景值；V为yi对xi的单个指标损益值的前景值。

（三）匹配优化模型构建与求解

风险投资机构和创业企业之间获得稳定匹配结果的前提条件是各自的满意度最大化，即

其中，（1）式表明风险投资机构X对创业企业Y的前景值最大化；（2）式表明创业企业Y对风险投资机构X的前景值最大化；（3）式、（4）式为限制条件，即一家风险投资机构可以投资多个创业企业，而一个创业企业只能接受一家风险投资机构；（5）式表明，当τij=0时，xi与yj不匹配，当τij=1时，xi与yj匹配。 然后，将多目标规划模型转化为单目标规划模型进行求解。

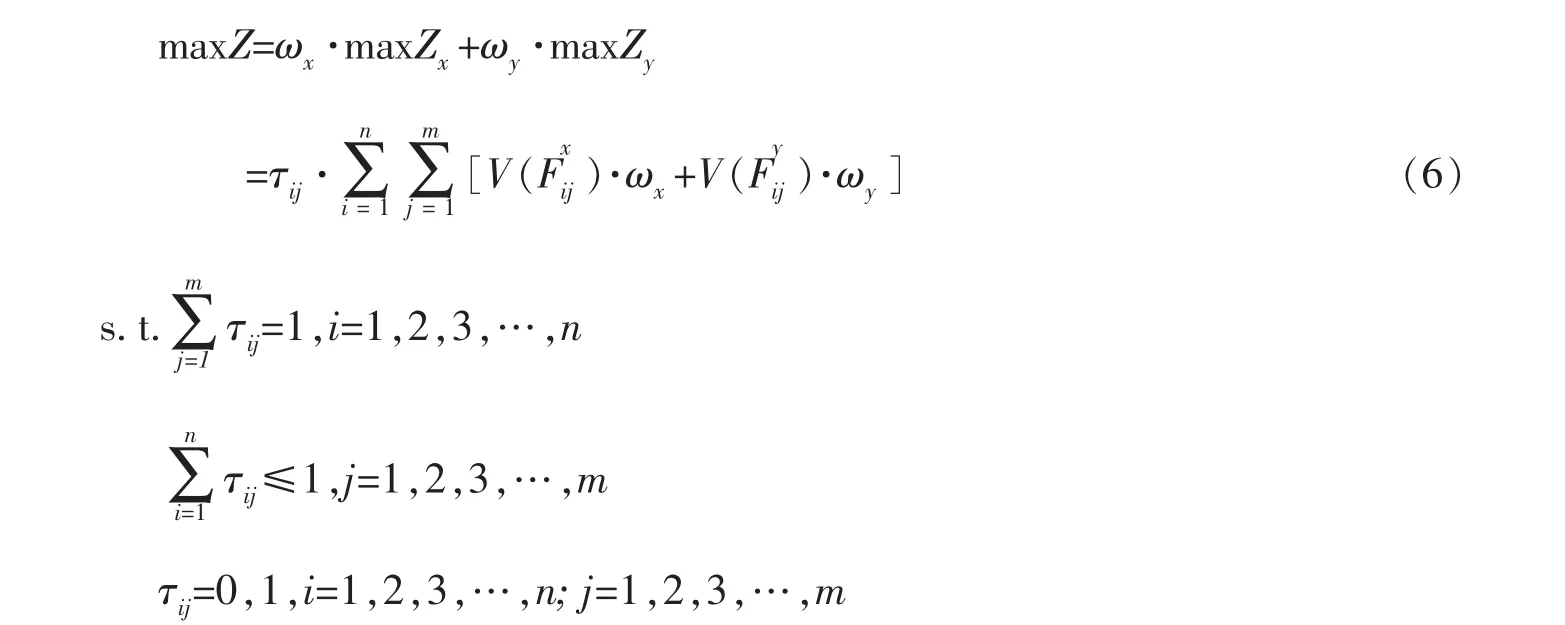
单目标规划模型可用LINGO 12.0 软件进行求解，而根据多目标规划理论，单目标规划模型的最优解也是多目标规划模型的最优解，所以以上决策模型可获得最优匹配方案。

四、算例分析

设风险投资市场的三方主体为4 家风险投资机构（x1，x2，x3，x4）、6 家创业企业（y1，y2，y3，y4，y5，y6）和投资中介。风险投资机构选取投资回报率a1、企业家素质a2、投资环境a3、投资回收期a4、技术水平a5等5 项指标对创业企业进行评价， 并使用预先给定语言短语集S和离散得分集T得到5项指标的期望信息，如表1所示。创业企业根据投资意愿b1、投资回报率b2、声誉b3、投资策略b4等4 项指标对风险投资机构进行评价，得到4 项指标的期望信息，如表2所示。 S={Sθ：θ=0，1，2，…，6}为语言短语集，其中，S0表示“极不满意”，S1表示“很不满意”，S2表示“不满意”，S3表示“一般”，S4表示“满意”，S5表示“很满意”，S6表示“极满意”。 T={1，2，3，4，5，6，7}，其中，1表示“极不满意”，2表示“很不满意”，3表示“不满意”，4表示“一般”，5表示“满意”，6表示“很满意”，7表示“极满意”。

表1 风险投资机构对创业企业的期望信息

投资中介在收到创业企业的融资需求信息和风险投资机构的投资需求信息之后分别对其进行综合调查评估， 得出6 家创业企业和4 家风险投资机构的实际评价信息， 分别如表3和表4 所示。

表2 创业企业对风险投资机构的期望信息

表3 创业企业的实际评估信息

表4 风险投资机构的实际评估信息

根据需求期望信息和实际评估信息，利用公式（1）、（2）、（3）、（4），分别计算出风险投资机构和创业企业的单个指标损益值。 然后，通过（2）式将损益值转化为表示满意度的综合前景值，如表5、表6 所示。 其中指标权重集ux取值为取值为

表5 风险投资机构的综合前景值

表6 创业企业的综合前景值

为了获取风险投资机构与创业企业的稳定匹配，使双方的满意度最大化，即双方的前景值最大化， 需要引进竞争度系数ωx与ωy， 将多目标规划模型转化为单目标规划模型进行求解。根据风险投资机构和创业企业的数量，ωx的值为0.6，ωy的值为0.4。利用LINGO 12.0 软件求解，其优化结果如表7 所示。

表7 风险投资机构与创业企业稳定匹配的优化结果

从表7 可以得出最终的匹配结果为：（x1，y5）、（x2，y1）、（x3，y2）、（x4，y3）、（x4，y4）、（x4，y6），即x1与y1匹配、x2与y5匹配、x3与y2匹配、x4与y3、y4、y6匹配。 该结果是考虑风险投资机构和创业企业的多类型需求信息所做出的，可为投资中介机构提供决策支持。

五、结论

本文根据风险投资机构与创业企业匹配的需求信息多元化特点，引入前景理论，构建了基于不同需求信息类型的双边匹配模型。 首先，将匹配主体不同类型的需求信息进行分类并将自身需求信息的期望值作为参照点，将投资中介所得到的双方实际评价信息相对于参照点转化为损益值。 其次，根据前景理论，即风险决策者在面临收益时是风险规避的，在面临损失时是风险偏好的，且对损失更加敏感的心理特征，将损益值转化为综合前景值，以双方综合前景值（满意度）最大化构建多目标优化模型，求解该模型得到最优匹配解。 最后，用实例证明了该模型在风险投资机构与创业企业的匹配问题上是有效的、可行的。