基于超表面材料的扇出衍射光学元件

陈奎先，王 宇，何桃桃，崔 圆，陶 金，李子乐，郑国兴,

(1.武汉大学 电子信息学院，湖北 武汉 430072;2.武汉邮电科学研究院 光纤通信技术与网络国家重点实验室，湖北 武汉 430074)

引言

近年来，随着科学家和学者的深入研究，关于超表面材料的研究成果不断涌现，发现其具有许多不同寻常的光学性能和一些有趣的物理现象[1-7]。在各种超表面材料中，几何超表面材料(GEMS)是由一系列空间朝向不同的纳米砖构成的超表面结构，其表现出很强的相位调控能力。因为几何超表面材料可以在亚波长波段产生任意相位轮廓，所以在设计复杂的纯相位型光学元件(超透镜、光栅和计算全息片等)时，几何超表面材料将会发挥其优势，为设计提供新的方法和思路[10-30]。

过去的几年中，在可见光波段和红外波段对基于贵金属的几何超表面材料全息片进行了研究[8-10]，尽管金属-绝缘体-金属(MIM)结构已经实现了具有高效率和高保真度的全息片，但到目前为止还不能避免金属材料中存在的固有欧姆损耗。由此可知，采用低损甚至无损的电介质材料替代金属，所得到的几何相位超表面光学元件在保证功能完整性的同时，性能也得到提升。众所周知，一个理想的几何超表面材料可以看成半波片来使用，入射光束经过几何超表面材料后，会在长轴和短轴2个偏振方向之间产生相位延迟π。与金属几何超表面材料不同，电介质几何超表面材料每个纳米砖轴向的有效折射率具有相对非常小的差异，因此，电介质几何超表面材料的深度(对于TiO2而言为入射光波波长约为λ[3]，对于硅而言约为λ/1.7[2])远远高于金属几何超表面材料(λ/27)[1]，这同时也涉及到制造极高深宽比的纳米结构(对于可见光范围内的TiO2来说，深宽比为6.3～15[1]，对于光纤通信窗口中的硅来说，其深宽比为4.8[2])。虽然目前已经出现了能够制造高深宽比超表面材料的原子层沉积技术[1](ALD)，但是大规模的制造和低成本仍然是未来投入实际应用中面临的挑战。

在早先的工作中，我们通过理论分析已经证明，工作在传输模式下的全硅纳米砖阵列可以精确地调控入射光的相位分布[2]。在本文中，我们将会通过理论分析，仿真和实验证明，玻璃上硅纳米砖结构在发生米氏共振反射时，同样具有很好的相位调节功能。对于这些精心设计的纳米砖阵列来说，通过调节每个纳米砖的转角，可根据需要将入射光束分成若干衍射级，同时保持入射光束的形状不变，即构成扇出衍射光学元件。这种超小型扇出衍射光学元件可以在光学传感、激光雷达和激光加工等许多领域中发挥优势。

1 设计仿真

设计了一个典型的纳米砖结构，并通过电磁仿真软件CST进行了仿真。建立好纳米砖单元之后，用一束圆偏振光(CP)入射到单元结构上，通过扫描纳米砖单元结构的几何参数来优化性能，如图1所示。纳米砖可以在x-y平面中旋转，转角为Φ，平面1和平面2分别位于纳米砖单元的中间，并分别与长轴和短轴平行，箭头分别表示平面1中的磁场(H)和平面2中的涡旋电场(E)分布。

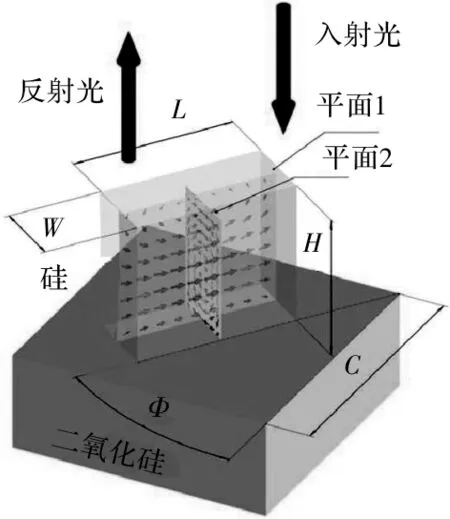
图1 纳米砖单元结构及共振原理示意图Fig.1 Schematic diagram of nanobrick unit structure and resonance principle

在数值模拟过程中，用一束沿着z轴波长为633 nm左旋圆偏振光(LCP)直接照射到具有周期性边界条件的纳米砖单元上，并且通过输出端口收集反射的交叉偏振光和同向偏振光。由于其他模式的能量占比非常低，故可以忽略不计。在电介质几何超表面材料中，高反射效率源于电共振或磁共振行为，λ=633 nm附近波长的磁共振行为如图1所示，平面1和平面2均位于纳米砖的中间，分别平行于纳米砖的长轴和短轴。在平面1中，磁场集中在纳米砖的中心并且发生增强，而在平面2中，在磁场周围存在涡旋状的电场分布，并在每个图像中将电场和磁场幅度归一化到其最大值。

这里初始设置的纳米砖单元结构高度H为170 nm，长度L为250 nm，宽度W为110 nm，单元尺寸CS为400 nm，深宽比约为1.545。通过结构参数的扫描来验证并优化圆偏振光偏振转换效率，扫描结果如图2(此时L=265 nm，W=125 nm，H=220 nm，CS=400 nm)所示。

图2 同向偏振和交叉偏振的反射率 (波长从500 nm到700 nm)Fig.2 Reflectivity of cross-polarized and co-polarized light versus wavelength(500 nm～700 nm)

图2显示了随着入射波长变化交叉偏振光和同向偏振光的反射率变化情况，可以看出，在波长为633 nm时，交叉偏振光的反射率为0.139 7，不需要的同向偏振反射率仅为0.031%，保证衍射零级功率低的同时，衍射光学元件又具有很高的衍射效率。

由于纳米砖之间的间隔较小，相邻纳米砖之间的近场耦合效应可以引起很小的波动，但如果2个临近纳米砖相互靠近，则耦合效应会很强，而当它们相距较远时则很弱。图3显示了光波反射率和相移θ与纳米砖的转角Φ的关系，可以很明显看出Φ和θ之间存在近似的线性关系，即θ约为Φ的两倍，即纳米砖单元作为半波片工作，并且连续地调制入射平面波的相位从0到2π。此外，交叉偏振光的反射率保持在12.89%以上，同时同向偏振光的反射率保持在0.031 4%以下，可以看出转角对振幅的影响较小。进一步模拟交叉偏振光束(LCP到RCP，反之亦然)的相位偏差与设计值的相位偏差(转角的两倍)，对于工作波长为633 nm的几个临近波长，如图4所示，其相位偏差约为1°～-12.8°，波长为633 nm时的最大绝对相位偏差为10.5°。

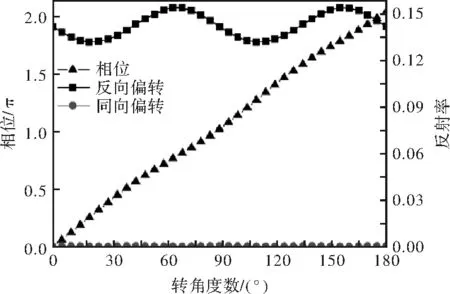
图3 同向偏振反射率、交叉偏振反射率和相移θ与纳米 砖转角Φ的关系(λ=633 nm)Fig.3 Reflectivity in power and phase shift versus orientation angle Φ. Cross-polarized light reflective efficiency- angle relation, co-polarized light reflective efficiency- angle relation and phase shift-angle relation (wavelength is set with 633 nm)

图4 工作在不同波长下的相邻纳米砖引起的近 场耦合效应对相位偏差的影响Fig.4 Simulated phase deviation caused by near-field coupling of adjacent nanobricks at different working wavelengths

利用上述的单元结构尺寸参数构建了纳米砖单元，实现了扇出衍射光学元件。图5(a)显示了扇出衍射光学元件的工作原理，设计单元尺寸为400 nm×400 nm，光栅周期为6.8 μm×6.8 μm，工作波长为633 nm。一个周期内的相位分布如图5(b)所示。当任意偏振态的光波垂直入射到纳米砖阵列时，在远场中将产生发散角为32°的矩形4×4均匀光斑阵列，其光斑阵列仅由16个奇数衍射级组成，零级、偶数级和其余的奇数级都被消除。值得一提的是，任意偏振态的光入射到衍射光学元件上，其交叉偏振的出射光会受到反向的相位延迟，这导致夫琅禾费衍射的光场分布绕其中心旋转180°。众所周知，任意偏振态的光束都可以分解成LCP光束和RCP光束，此外，4×4光斑阵列即使围绕其中心旋转180°也保持不变，因为它是中心对称图案，因此，这种扇出衍射光学元件对入射光的偏振态并不敏感。这里我们采用经典的Gerchberg-Saxton算法获得达曼光栅的相位分布，纳米砖阵列的转角根据Φ和θ的关系来排列。

图5 扇出元件工作原理图及仿真结果Fig.5 Working principle and simulation results of fan-out elements

为了研究达曼光栅的性能，采用了CST MWS中的有限积分技术(FIT)，在时域中模拟扇出衍射元件，并利用远场监视器收集光场分布。图5(c)显示了远场中衍射场的功率分布，横坐标和纵坐标分别表示x和y方向的顺序，一般来说，所需的衍射级次是清楚的，虽然可以看到由纳米砖近场耦合效应引起的零级，但其功率仅占这些可见衍射级次功率的2%。

2 实验验证

如图6(a)所示，采用该实验装置来验证基于超表面材料的扇出衍射光学元件的性能。由He-Ne激光器产生的激光束垂直入射到长焦透镜上，然后通过透镜的激光聚焦在样品上，该样品安装在三维平移台上，可以自由调整样本位置。样品上的光斑半径约为0.5 mm，以便通过平面波来照射该样品表面，不同衍射级的反射光束可以在远场中观察到并由商业相机捕获。屏幕是白板，中心有一个孔(直径9 mm)，允许入射光和反射光的零级通过。图6(b)显示了图像平面上的衍射矩形4×4点阵列，样片和屏幕之间的距离为300 mm，波长为633 nm。我们注意到斑点的位置不会发生偏移，并且功率分布几乎是均匀的。为证明扇出衍射元件对入射光偏振态不敏感，分别用LCP光束和RCP光束照射样品，结果几乎保持不变，与理论预测吻合良好。

图6 扇出元件的实验装置及验证结果Fig.6 Experimental devices and verification results of fan-out elements

对于二维周期性的衍射器件，当平面波垂直入射时，每个衍射级次的位置可以由以下公式计算：

(1)

式中：α和β分别表示衍射角和方位角；i和j表示x和y方向中的衍射级次；λ是入射光的波长；n是介质的折射率，反射光所处的介质通常是真空或空气(n=1)；px和py分别是x和y方向的光栅周期(在该样品中，px=py)。当我们设置衍射距离为z=300 mm，可以根据(1)式来计算各个级数的位置，并与图6(b)的实验结果进行比较，发现实验结果和理论预测一致。

为了评估基于超表面材料的扇出衍射光学元件的性能，我们还测量每个衍射级和输入光的功率，并且将均匀性定义为(Imax-Imin)/(Imax+Imin)，其中Imax和Imin是所需衍射级次光斑的最大和最小功率。零集效率(ZOE)定义为输入功率除以零级功率。在我们的实验中，ZOE测试为22.03%，高于理论值，这可能是由制造误差引起的，所需衍射级次的均匀性为24.3%，均匀性的偏差主要是相邻纳米砖与制造误差引起的近场耦合效应以及加工误差所导致的。

3 结论

提出一种基于电介质几何超表面材料的扇出衍射元件的设计方法，它可以连续精确地调制入射光的相位，以这种方式设计的衍射光学元件可以克服传统深度控制衍射光学元件的固有台阶缺陷，转角并且共振模式工作使纳米砖具有较低的深宽比，极大地降低了超表面的制造难题。这类新型衍射光学元件的出现，将为纯相位衍射器件的深入发展铺平道路，并将促进诸如全息术、光纤通信和数据存储等领域的发展。