AOTF成像光谱仪声光晶体光谱传递函数的研究
2019-03-23常凌颖宋晶晶靳梦竹
常凌颖,宋晶晶,靳梦竹
(西安邮电大学 电子工程学院,陕西 西安 710121)
引言
光谱成像技术是一种将光谱和成像技术结合起来,同时获得被测目标的几何信息和光谱信息,而基于声光可调谐滤波器(acoustic-optic tunable filte, AOTF)的成像光谱仪具有谐调速度快、大孔径、实时成像、没有运动部件等优点,在农业、工业、航空航天业,生命科学等多个领域得到广泛的应用[1-3]。
仪器的传递函数是衡量仪器性能的一项重要指标,光学传递函数是表述仪器空间的分辨能力,而光谱传递函数是表述光谱的分辨能力。目前,成像光谱仪光学传递函数的设计优化方法已日趋完善[4],随着成像光谱仪的发展,需要在高空间传递函数条件下能获得高的光谱传递函数。美国航空航天局(NASA)Katzberg、Statham等通过光谱调制简化分析了阵列型光谱成像仪的光谱传递特性[5];中国科学院西安光学精密机械研究所相里斌、王新全等通过等效光路图研究了傅里叶型和光栅型光谱成像仪的光谱传递函数,提出了光谱数据恢复的新方法,但忽略了仪器自身色散的影响[6-7];浙江大学赵烈烽、徐之海等人通过引入采样模型分析了色散型光谱仪对典型高斯谱线平均混叠误差的影响,没有针对色散元件本身综合分析光谱传递特性[8]。
光谱传递函数是仪器分辨率与透过函数的综合表述,成像光谱仪的核心分光元件不能同时具有不同的光谱传递函数表达式,本文利用光学域光谱透过函数,推导了以波数Δv表示单、双型AOTF的光谱传递函数。在光谱域中,双AOTF型与单AOTF型光谱传递函数进行了对比分析,并探讨了声光互作用长度L,入射光极角θi及入射光波长λ对双AOTF光谱传递函数的影响,研究结果为提高AOTF光谱成像仪的性能提供了理论参考数据。
1 AOTF的成像光谱仪工作原理
1.1 单AOTF型工作原理
单个成像型AOTF由声光晶体(TeO2),压电换能器,吸声体、挡光板组成,如图1所示。超声换能器上加载电信号,电信号在晶体内转换成声波,晶体光轴沿001方向,为了防止声波反射,透过介质的声波被吸声体吸收。当入射光为白光时,与超声波一起产生非线性作用,满足动量匹配条件时,入射光在声光互作用区产生布拉格效应,除了零级光透射外还衍射出两束光,一束为正衍射光,一束为负衍射光,分别位于零级光两侧,改变超声波频率则改变衍射光波长[9-10]。
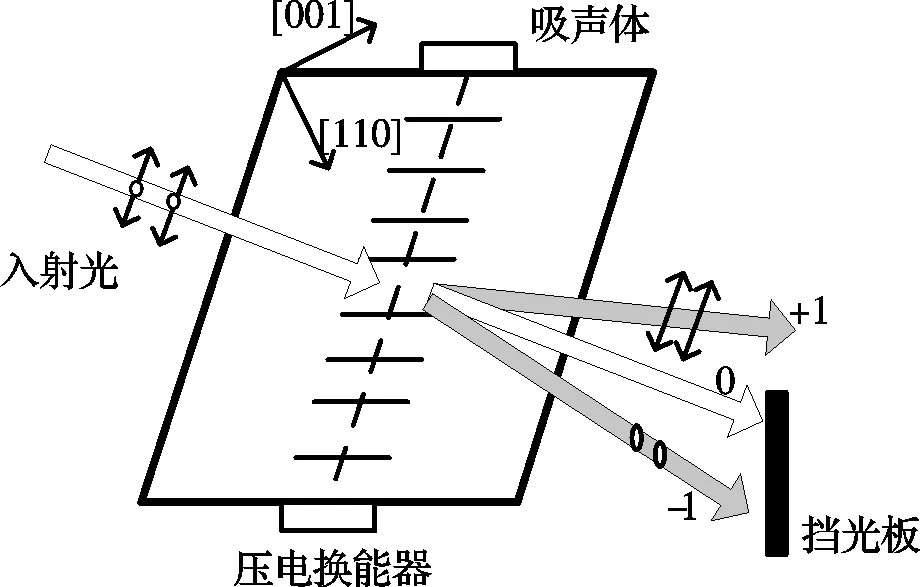
图1 单AOTF的工作原理图Fig.1 Working principle diagram of single AOTF
1.2 双AOTF型工作原理
为了提高光谱分辨率,可以通过2个AOTF的串联提高器件的光谱分辨率[11]。
双AOTF型成像光谱仪的分光单元是由2个独立的声光可调滤波器组成,如图2所示。2个主平面光轴相互平行,保证从第1个AOTF调谐出的光波平行入射到第2个AOTF中,2个超声换能器的信号频率可单独调谐,控制2个AOTF中心波长的差值,实现二次滤波[12]。

图2 双AOTF的工作原理图Fig.2 Working principle of dual AOTF
2 单AOTF型光谱成像仪声光晶体的光谱传递函数
光谱传递函数是光谱信息传输的一种综合体现,研究光谱传递函数能够直接从光谱域分析出仪器的性能特征。
2.1 用Δv表示的光谱透过函数
AOTF衍射光光强I0与入射光光强Ii的比值即为AOTF光谱透过函数h(Δv)[13]:
(1)
2.2 用λ表示的光谱透过函数
基于耦合波理论,并将光谱透过率函数进行归一化处理。设Γ·L=π/2,取L=5 mm,此时理论衍射效率达到最大值[14]。在平行光入射时,声光晶体的光谱传递函数在小波长范围内只与衍射光的波数差Δv有关,由(2)式可得到用λ表示的光谱透过率函数h(λ):
(2)
由(2)式可知,λ0为入射光中心波长,λ为衍射光波长,对为于不同入射光波长,光谱透过函数都呈Sa函数形式。以入射光波长λ=650 nm为例,讨论单AOTF型光谱成像仪声光晶体光谱透过函数。经归一化处理,光谱透过函数如图3所示。

图3 单AOTF晶体光谱透过函数Fig.3 Single AOTF crystal spectral transmission function(λ=650 mm,θi=30°,L=5 mm)
图3中横坐标是波长,单位为nm,纵坐标为光谱透过率函数h,归一化为1,λ为中心波长,r(λ)为衍射光展宽的半高全宽(FWHM)。由图3可以看出,中心波长处光谱透过率最高,随着衍射光波长的递增和递减,光谱透过率以sinc2函数递减。
取3个半高宽内的光谱传递函数进行讨论分析[15],此时光谱传递函数h(λ0)可表示为
h(λ0)= sinc2(λ0)+a1sinc2(λ0-λ1)+
a-1sinc2(λ0-λ-1)
(3)
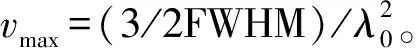
2.3 单AOTF型光谱成像仪声光晶体的光谱传递函数
由于AOTF光谱仪在小波长范围内满足线性不变性,设入射光光谱强度为o(v),在忽略噪声的情况下,可得到通过光谱仪后衍射光的光谱强度d(v),如下式所示:

(4)
由(4)式可知,当波数差小于0时,不具有物理意义,定义v≤0时,o(v)=0。将光谱透过函数在波数差范围内积分就可以得到光谱传递函数[16],现在将单AOTF型光谱成像仪声光晶体的光谱传递函数进行傅里叶变换并归一化得到AOTF光谱传递函数H(f),f为单位波数间隔的谱线数,如下式所示:
(5)
则仪器的光谱传输为
D(f)=H(f)·O(f)
(6)
式中:D(f)、O(f)分别为输出光与输入光的光谱强度归一化傅里叶变换。
基于AOTF型成像光谱仪的光谱分辨率为[17]
(7)
式中:λ为入射光波长;b为色散系数;L为声光互作用长度;θi为入射光极角。
将(3)式~(7)式联立,得到单AOTF型光谱成像仪声光晶体的光谱传递函数H(f)为
(8)
式中:最大波数差vmax=2.7π/bLsin2θi;λ为入射光波长;b为色散系数;L为声光互作用长度;θi为入射光极角;f为单位波数间隔的谱线数。
3 双AOTF型成像光谱仪声光晶体的光谱传递函数
在推导了单AOTF型光谱成像仪声光晶体的光谱传递函数的基础上,推导双AOTF型光谱成像仪声光晶体的光谱传递函数来进行对比。
3.1 用Δv表示的光谱透过函数
当AOTF1中心波长λ1不变的情况下,由(9)式可得:
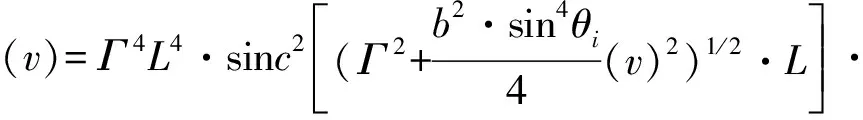
(9)
式中:Γ值为定值;λ1、λ2分别为AOTF1和AOTF2的中心波长;b为色散系数;L为声光互作用长度,θi为入射光极角,v为衍射光波数差。
3.2 用λ表示的光谱透过函数
λ表示的光谱透过函数为
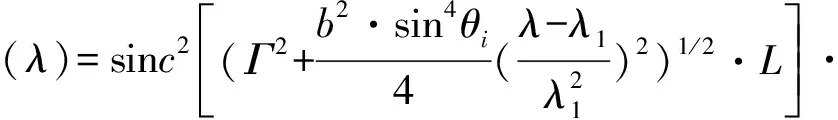
(10)
式中:透过因子Γ为定值;λ1、λ2分别为AOTF1和AOTF2的中心波长;b为色散系数;L为声光互作用长度;θi为入射光极角;λ为衍射光波长;两声光晶体的声光互作用长度L和入射光极角相等。
取AOTF1、AOTF2的声光互作用长度L=5 mm、入射光极角θi=30°,AOTF1中心波长取650 nm,调整AOTF2中心波长分别为650.5 nm和651 nm。
此时双AOTF型光谱透过函数h总(λ)如图4所示。从图4中可以看出,随着AOTF2与AOTF1中心波长的差值加大,半高宽FWMH由1.4 nm降到1.2 nm,光谱透过值由0.9降到0.64,说明随着AOTF2与AOTF1中心波长差值的增大,双AOTF的半高宽FWMH在减小,光谱透过函数也在减小。
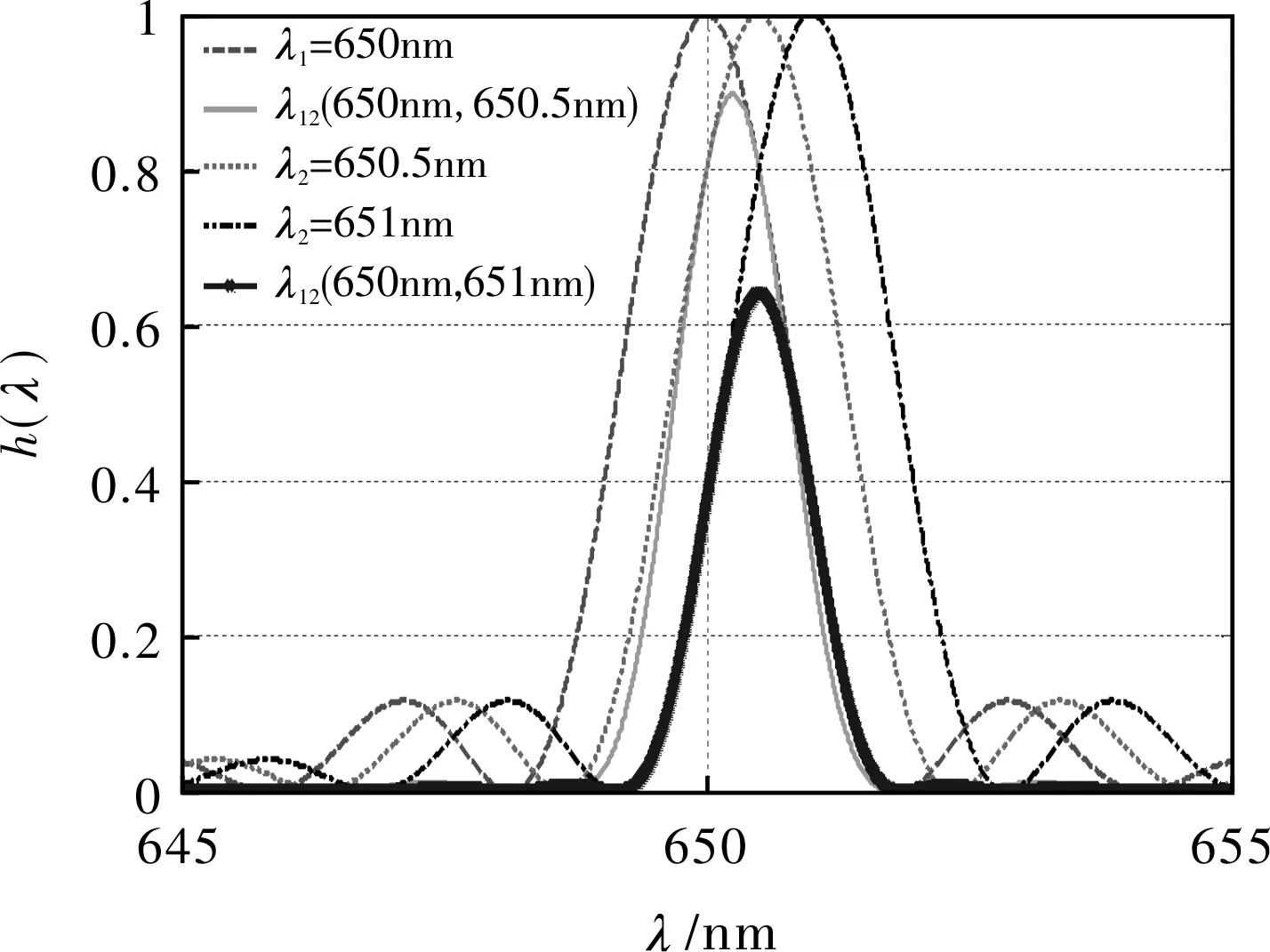
图4 双AOTF晶体光谱透过函数Fig.4 Single AOTF crystal spectral transmission function
3.3 双AOTF型光谱成像仪声光晶体的光谱传递函数
由于AOTF型成像光谱仪的光谱传递函数是对光谱透过函数在波数差范围内积分得到的结果,当λ1、λ2、θi、L、确定的情况下,双AOTF型成像光谱仪的光谱透过函数只与衍射光的波数差有关。将(4)式、(5)式、(7)式和(10)式联立可得双AOTF光谱传递函数H(f)为

(11)
其中vmax会因为FWMH的变化而发生变化。AOTF1和AOTF2串联后,FWMH在减小,vmax相应也减小,AOTF1和AOTF2中心波长相等时vmax对传递函数影响最大。当AOTF1=AOTF2=650 nm,L=4 mm,θi=30°时,由FWMH导致的vmax减小使光谱传递函数截止频率由0.038 cm-1增加到0.039 cm-1,仅增加了0.25%,可忽略不计。
4 AOTF型光谱成像仪声光晶体的光谱传递函数比对
由2.3节和3.3节得到了以波数Δv表示单、双AOTF型的光谱传递函数,由(8)式、(11)式从单、双AOTF型的光谱传递函数的表达式可以看出,两者形式相似,不同之处在于光谱透过函数的差异,在工作波段为400 nm~900 nm范围内,改变波长,以入射光波长λ=650 nm为例,讨论单、双AOTF型光谱成像仪声光晶体光谱传递函数的差异。
4.1 AOTF1和AOTF2中心波长相等时声光晶体的光谱传递函数
分别取单AOTF型的入射光波长λ=650 nm、400 nm、900 nm,对应双AOTF型的AOTF1和AOTF2的中心波长均为650 nm、400 nm、900 nm,图5为中心波长不同时,单、双AOTF晶体的光谱传递函数对比图。
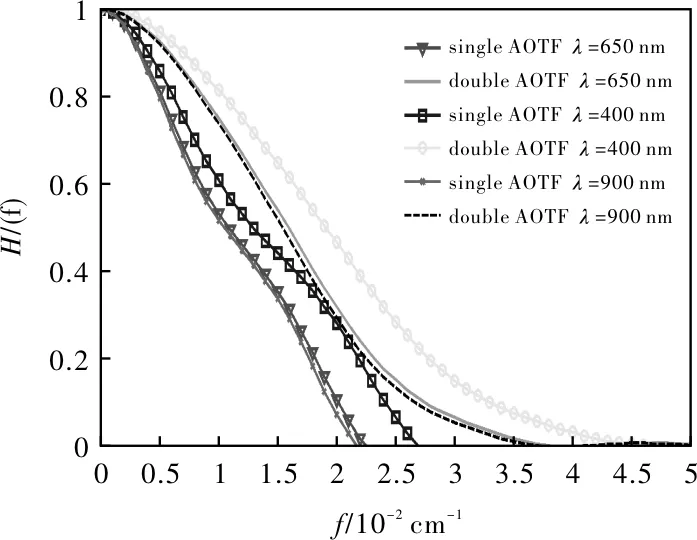
图5 单、双AOTF晶体的光谱传递函数对比图Fig.5 Comparison of spectral transfer functions between single and dual AOTF crystals(θi=30°,L=5 mm)
由图5可知,给定θi、L,相同入射光波长下,双AOTF型在相同中心波长下截止频率大于单AOTF,双AOTF型的平均光谱值为2.1/cm-1,单AOTF型平均光谱值为1.25/cm-1,光谱传递函数平均提高了68%;对于同一截止频率,双AOTF型的光谱传递函数明显优于单AOTF型的光谱传递函数。
4.2 AOTF1和AOTF2中心波长不相等时声光晶体的光谱传递函数
单AOTF型的入射光波长λ=650 nm,双AOTF型的AOTF1波长取650 nm, 调整AOTF2的中心波长从650 nm变动到652 nm,最大中心波长差为2 nm。
图6为AOTF1和AOTF2中心波长不相等时声光晶体的光谱传递函数与单AOTF型声光晶体的光谱传递函数的对比图。
由图6可知,虽然单AOTF光谱与双AOTF光谱存在交点,主要是由于对光谱图归一化处理以及双AOTF二次平滑所致,但截止频率并不受影响,所以分析截止频率更能反映出光谱特性,双AOTF型光谱传递函数随着AOTF1和AOTF2中心波长差的增大,光谱传递函数截止频率在减小。与单AOTF型成像光谱仪相比,双AOTF型成像光谱仪声光晶体的光谱传递函数并不绝对优于单AOTF型,具体分析计算图见表1所示。
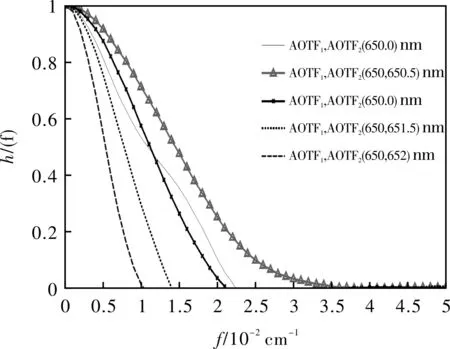
图6 AOTF1和AOTF2中心波长不相等时声光晶体 的光谱传递函数Fig.6 Spectral transfer function of acousto-optic crystals when AOTF1 and AOTF2 are not equal in center wavelength
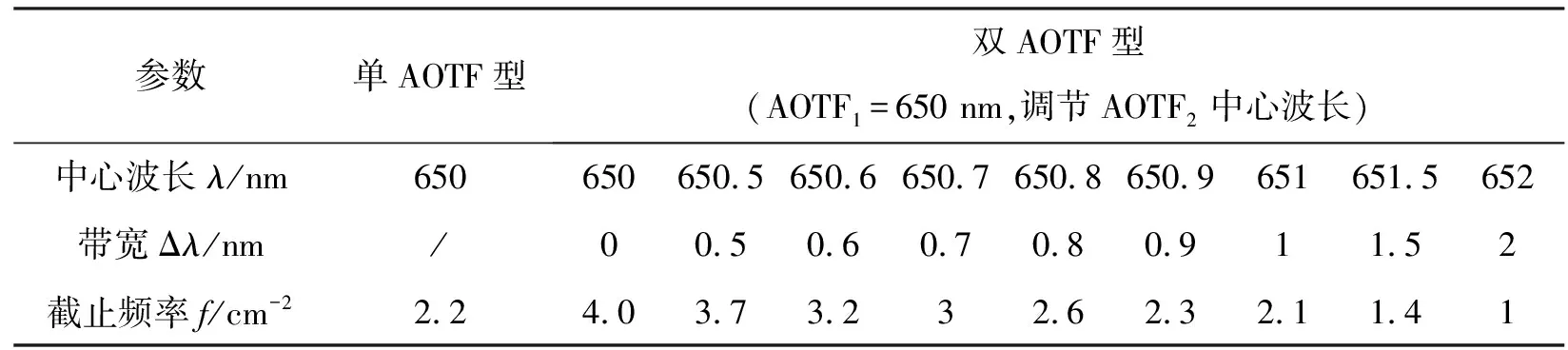
参数单AOTF型双AOTF型(AOTF1=650 nm,调节AOTF2中心波长)中心波长λ/nm650650650.5650.6650.7650.8650.9651651.5652带宽Δλ/nm/00.50.60.70.80.911.52截止频率f/cm-22.24.03.73.232.62.32.11.41
当AOTF2中心波长在650 nm~650.9 nm之间,截止频率从0.04 cm-1下降到0.023 cm-1,此时双AOTF型成像光谱仪声光晶体的光谱传递函数优于单AOTF型。当AOTF2中心波长在651 nm~652 nm之间,截止频率从0.021 cm-1下降到0.01 cm-1,双AOTF型成像光谱仪声光晶体的光谱传递函数略小于单AOTF型,通过光谱传递函数我们能读取出一个临界值,该临界值的物理意义为双AOTF晶体在保证单AOTF传递特性的基础上,可视为衍射效率的极小值和光谱分辨率的极大值。
5 影响双AOTF型光谱传递函数的因素分析
5.1 入射光极角θi对双AOTF晶体光谱传递函数的影响
AOTF型光谱成像仪最佳入射光极角θi为20°~30°之间[18],当AOTF1、AOTF2中心波长λ都为650 nm,L=5 mm情况下,双AOTF光谱传递函数与θi的关系如图7所示。
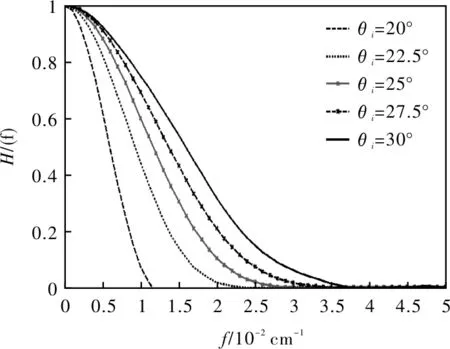
图7 双 AOTF晶体光谱传递函数与θi关系Fig.7 Relationship between spectral transfer function and θi of dual AOTF crystal
由图7可知,随着入射光极角θi的增大,截止频率f随之增大,当入射光极角θi从20°增大到30°,截止频率f从0.012 cm-1增加到0.037 cm-1,对于同一截止频率,随着入射光极角θi的增大,光谱传递函数也在增大。
5.2 声光互作用长度L对双AOTF晶体光谱传递函数的影响
AOTF声光互作用长度L=2.5 mm~10 mm,当AOTF1、AOTF2入射光极角都为θi=30°,入射光波长为λ=650 nm情况下,双AOTF光谱传递函数与声光互作用长度L的关系如图8所示。
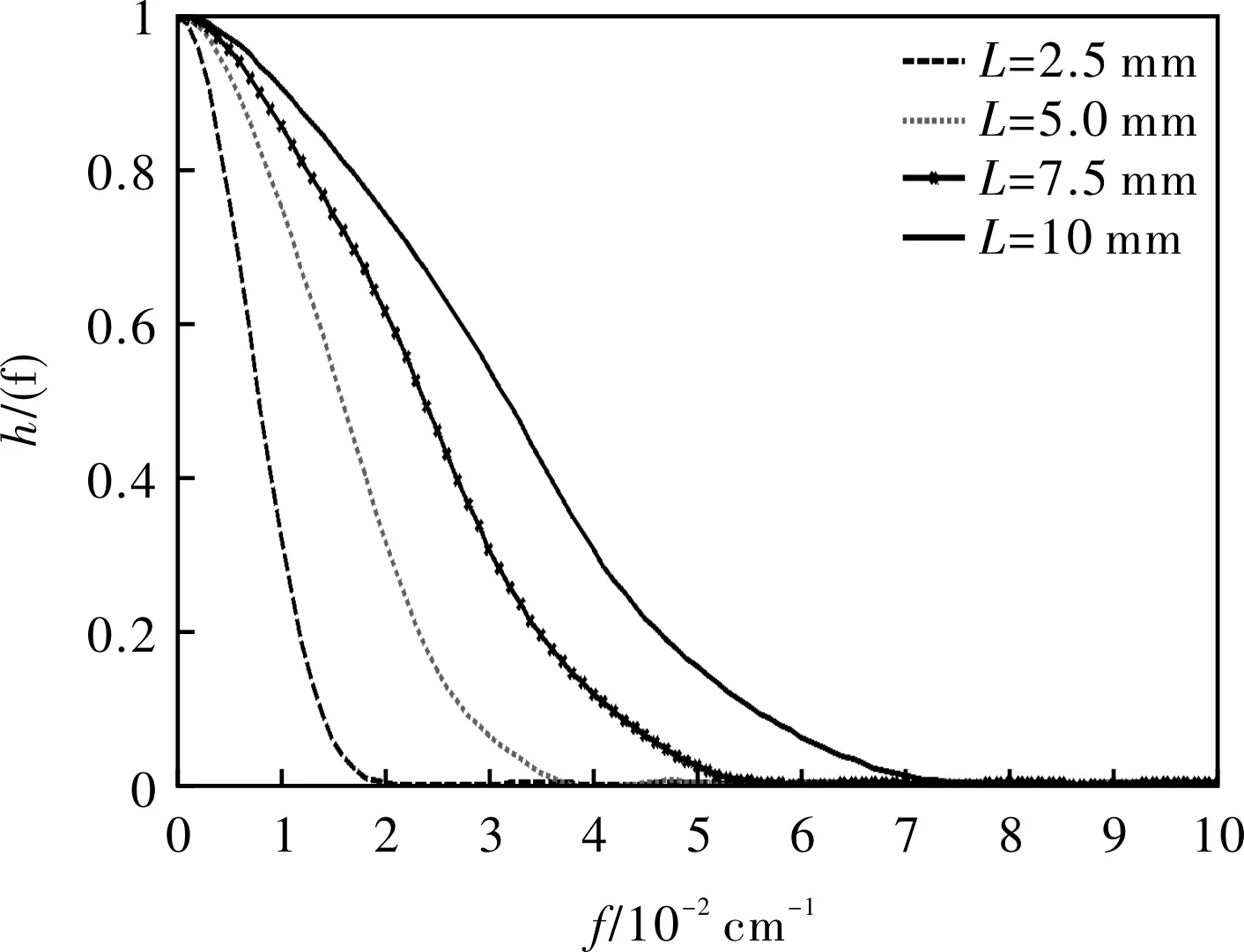
图8 双AOTF晶体光谱传递函数与L的关系Fig.8 Relationship between spectral transfer function and L of dual AOTF crystal
由图8可知,λ1=λ2=650 nm,θi=30°,双AOTF光谱传递函数在L=2.5 mm~10 mm之间,随着L的增大,截止频率从0.021 cm-1增加到0.077 cm-1。
5.3 入射光波长对双AOTF晶体光谱传递函数的影响
声光互作用长度L=5 mm,入射光极角θi=30°,AOTF光谱传递函数与入射光波长λ的关系如图9所示。
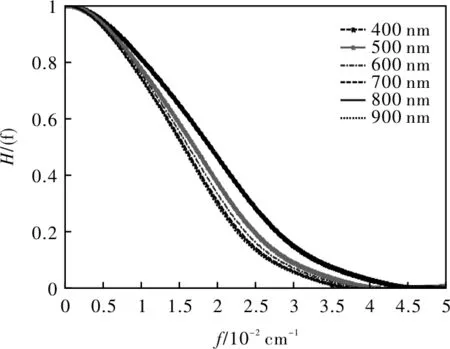
图9 双AOTF晶体光谱传递函数与λ的关系Fig.9 Relationship between spectral transfer function and λ of dual AOTF crystal
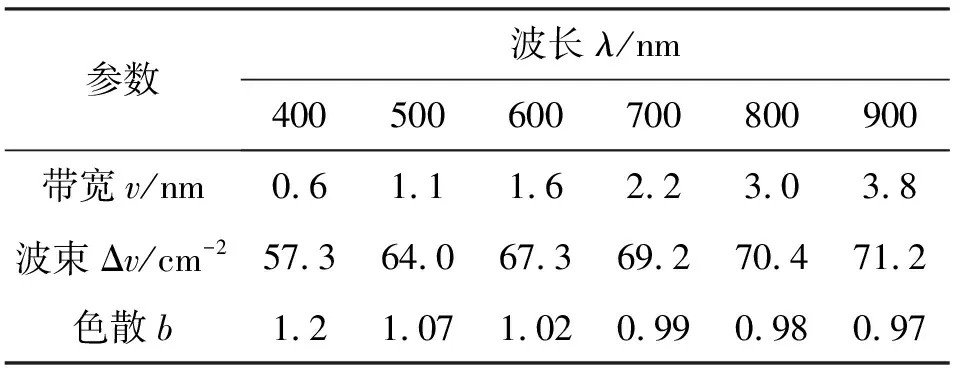
参数波长λ/nm400500600700800900带宽v/nm0.61.11.62.23.03.8波束Δv/cm-257.364.067.369.270.471.2色散b1.21.071.020.990.980.97
由图9可知,双AOTF光谱传递函数在波长400 nm~900 nm之间随着入射光波长的增大截止频率从0.045 cm-1下降到0.036 cm-1,表2为不同波长下的仿真参数。由表2、图9可知,随着入射光波长的增大,带宽和波束差Δv在增大,色散b在减小,截止频率f的降低实际上是由于色散导致的。入射光波长400 nm比900 nm光谱传递函数平均提高31.1%。选定λ,随着L、θi的增大,f截止频率越高。选取L、θi,λ值越小,f截止频率越高。说明在此工作波段研究双AOTF型光谱传递函数的时候,选取大的L即在制作工艺上选取多个L=2.5 mm压电换能器串联,θi=30°,λ=400 nm有利于提高光谱仪的截止频率,提升光谱传递特性。
6 结论
光谱传递函数是光谱成像仪透过函数与光谱分辨率的综合体现,对于提高仪器信息获取能力有重要的作用,本文推导了单、双AOTF型成像光谱仪声光晶体的光谱传递函数,结果表明,在θi=30°,L=5 mm,λ=400 nm~900 nm内,当双AOTF型成像光谱仪工作中心波长相等时,相比同一工作中心波长时的单AOTF型成像光谱仪,光谱传递函数提高了68%;当成像光谱仪工作中心波长不相等时,双AOTF型成像光谱仪声光晶体的光谱传递函数并不绝对优于单AOTF型,AOTF截止频率存在临界值,该临界值是相对单AOTF光谱分辨率提升的极限值。在工作波段400 nm~900 nm,入射光极角θi为30°,声光互作用长度L为5 mm,入射光波长在400 nm比900 nm时的光谱传递函数提高了31.1%。研究结果为提高AOTF光谱成像仪的性能提供了理论参考数据。
