一种基于UU磁心的VCC耦合电感研究
2019-03-23李志忠林佳庆
杨 慧,李志忠,林佳庆
(广东工业大学 信息工程学院,广东 广州 510006)
0 引 言
随着电力电子技术的迅速发展,耦合电感的应用领域越来越广泛。在多相交错并联磁耦合变换器中,采用最佳耦合系数的耦合电感,能明显提高变换器的稳态性能和暂态性能,并大幅降低变换器的体积和成本。当耦合电感的耦合系数在一定范围内变化时,多相交错并联磁耦合变换器的稳态性能和暂态性能达成统一,即变换器的稳态性能和动态性能相互促进[1]。因此,合理采用耦合电感的耦合系数对于兼顾变换器的稳态性能和暂态性能、减小变换器的体积至关重要。
目前,两相耦合电感的应用最广泛。采用EI磁心实现的两相耦合电感,结构简单,磁心数量小,制作方便,且磁心间有气隙不易饱和。但是,它的耦合系数值偏小,仅为1/3,不能兼顾变换器的稳态性能和暂态性能。当变换器的运行参数(如占空比)变化时,它的稳态性能和暂态性能随之改变[2]。通过改变绕组绕线方式实现的无气隙可变耦合系数的耦合电感,可得到各种耦合系数,提高了变换器的稳态性能和暂态性能,但其绕线方式复杂,不易制作,且磁心间无气隙易饱和,适用于小功率应用场合[3]。
本文提出了一种基于UU磁心的可变耦合系数的两相耦合电感结构,既兼顾了变换器的稳态性能和暂态性能,又适用于大功率应用场合。最后,通过理论分析和实验样机,验证了该耦合电感结构的有效性和耦合系数可变原理的正确性。
1 VCC耦合电感结构和可变耦合系数的原理
1.1 VCC耦合电感的结构
图1为基于UU磁心的VCC耦合电感结构,由两副同型UU磁心(1#~4#)组成,绕组N1、N2分别构成电感Ls1、Ls2。该耦合电感可看作是两个独立电感Ls1、Ls2相互耦合而成的。根据耦合电感绕组电流流向,分为正向耦合方式和反向耦合方式。
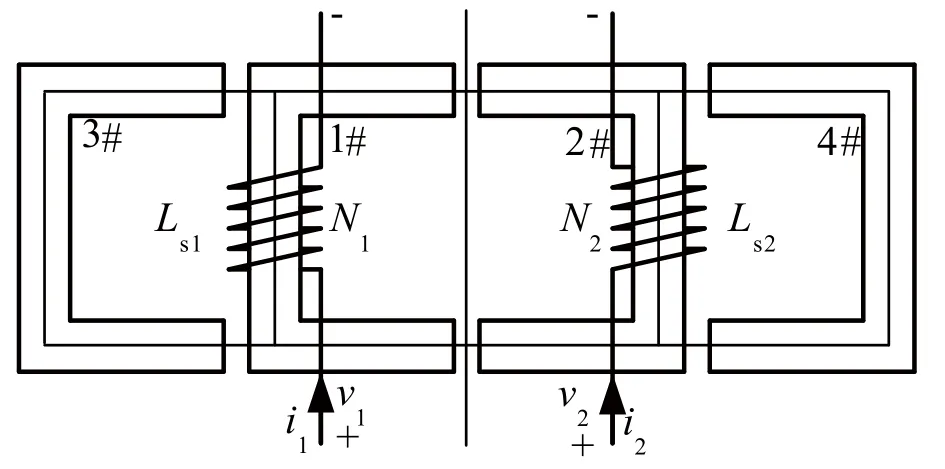
图1 基于UU磁心的VCC耦合电感结构
两相交错并联磁耦合变换器的耦合电感处于反向耦合方式[2],故本文只研究耦合电感反向耦合方式。如图1所示,v1、v2分别为N1、N2两端所加电压源,电流i1、i2流向均为从上到下。根据右手螺旋定则,判知电感Ls1和Ls2为反向耦合。
耦合方式为:
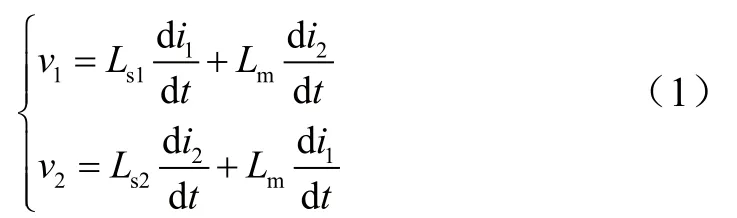
其中,Lm为互感。当Lm<0时,反向耦合;当Lm>0时,正向耦合。
1.2 可变耦合系数的原理
实际应用中,图1的耦合电感虚线两边磁心结构和绕组参数对称,故N1=N2=N,Ls1=Ls2=Ls。
图2为VCC耦合电感的电路模型。由一个N1∶N2理想变压器、一个励磁电感(互感)Lm和两个漏磁电感(漏感)Llk1、Llk2组成,理想变压器是以N1/N2比例变换初次级电压、电流[4]。

其中,Llk=Llk1=Llk2;k为耦合系数,反向耦合时为负,正向耦合为正。
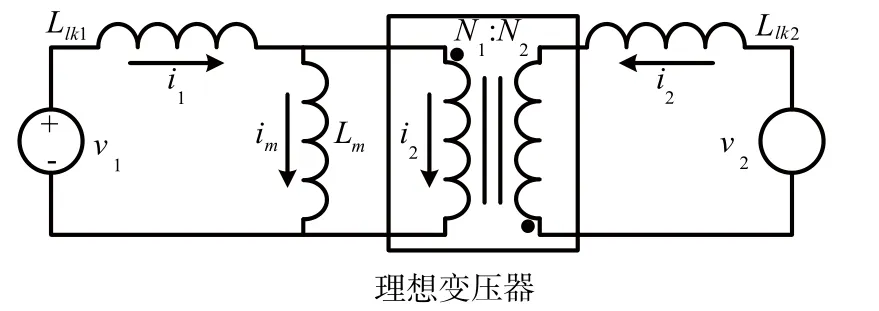
图2 VCC耦合电感的电路模型
建立VCC耦合电感的磁路模型,需先分析磁通分布。忽略绕组,在外部空气的漏磁磁通和气隙边缘效应情况下,磁通分布和各段磁路长度如图3所示。其中,实线、虚线分别代表N1、N2绕组电流i1、i2产生的磁通,Φ1、Φ2分别为通过N1、N2绕组主磁通;Φm为通过中间气隙的励磁磁通;Φlk1、Φlk2分别为通过两边气隙的漏磁磁通。a为磁心的磁柱长度;b为磁心的磁轭长度;gm为1#、2#磁心间的气隙长度;glk为1#、3#或2#、4#磁心间的气隙长度。
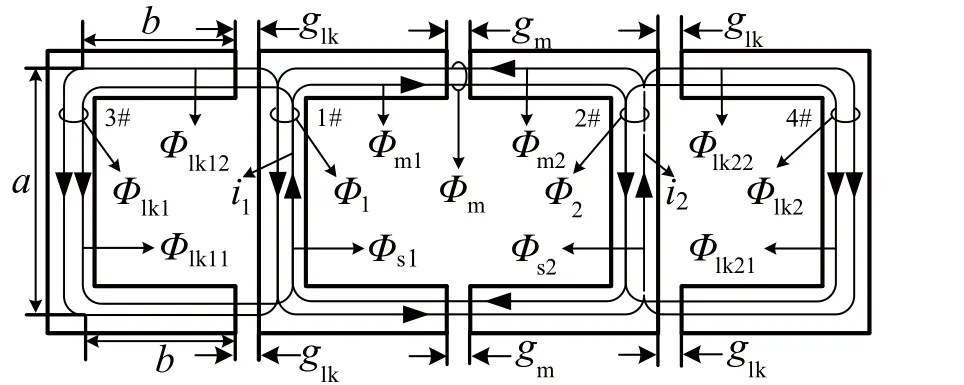
图3 磁通分布和各段磁路长度
根据磁路的欧姆定律,可得VCC耦合电感的磁路模型,如图4所示。其中,Ni1、Ni2分别代表N1、N1绕组磁势;Ria、Rib(i=1~4)分别代表1#~4#磁心a段、b段磁路的磁阻;Rgm、Rlk分别代表气隙gm、glk的磁阻。显然有Ria=Ra(i=1~4),Rib=Rb(i=1~4)。
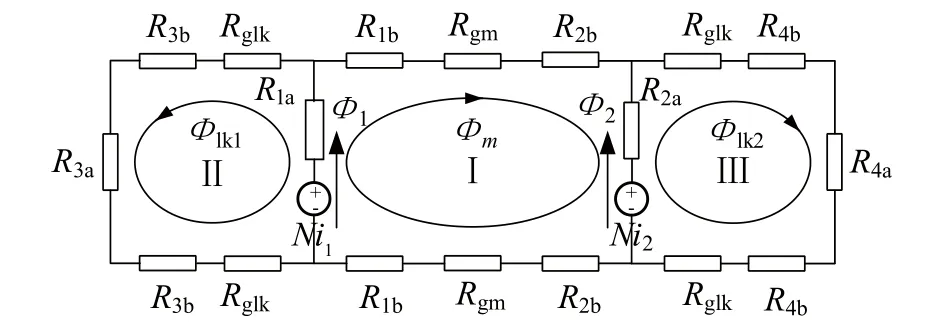
图4 VCC耦合电感的磁路模型
假设UU磁心的磁柱和磁轭横截面积都为A,根据磁阻定义得出图4中各段磁路的磁阻表达式为:
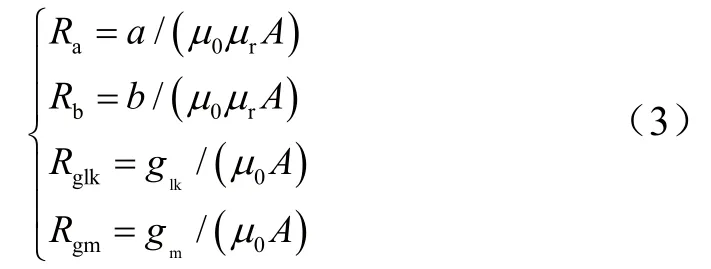
其中:μ0为空气磁导率;μr为磁心相对磁导率。对图4中的环路I、II和III运用高斯定理和安培环路定理,得出Ni1、Ni2表达式为:
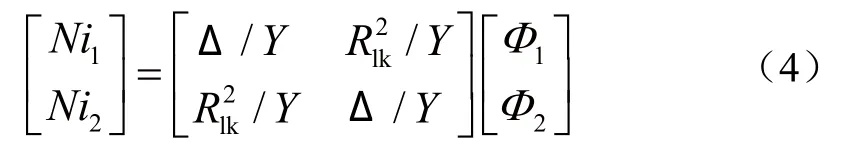
其中,Rm=2(2Rb+Rgm);R1k=Ra+2(Rb+Rglk);Δ=2RaR1k+RaRm+RmR1k+R21k;Y=Rm+2R1k。
从式(4)中解出Φ1、Φ2为:
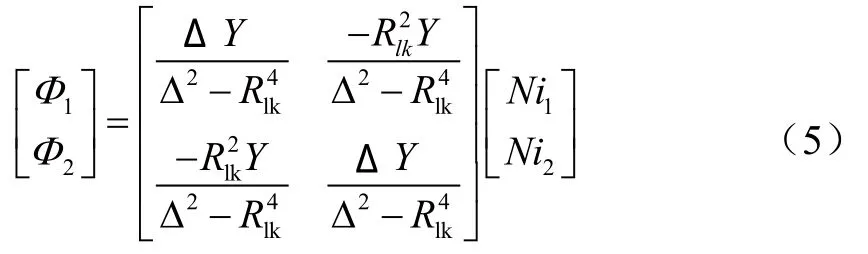
根据法拉第定理,得出N1、N2绕组两端电压v1、v2表达式为:
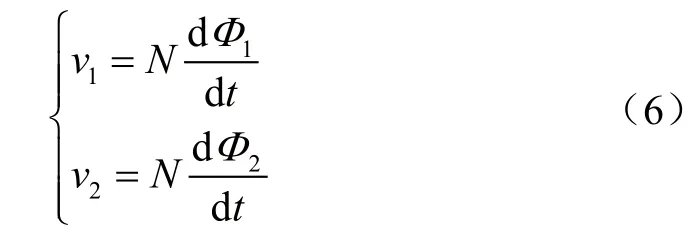
把式(5)代入式(6),并与式(1)比较,得出自感Ls和互感Lm的表达式为:
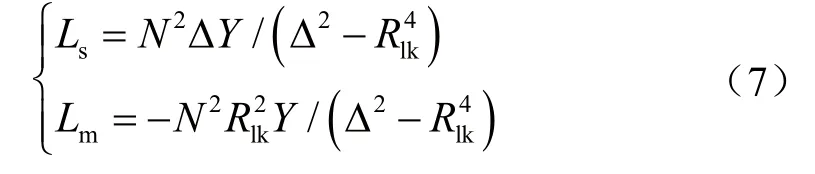
根据式(3)和式(7),求出VCC耦合电感的耦合系数k的表达式为:
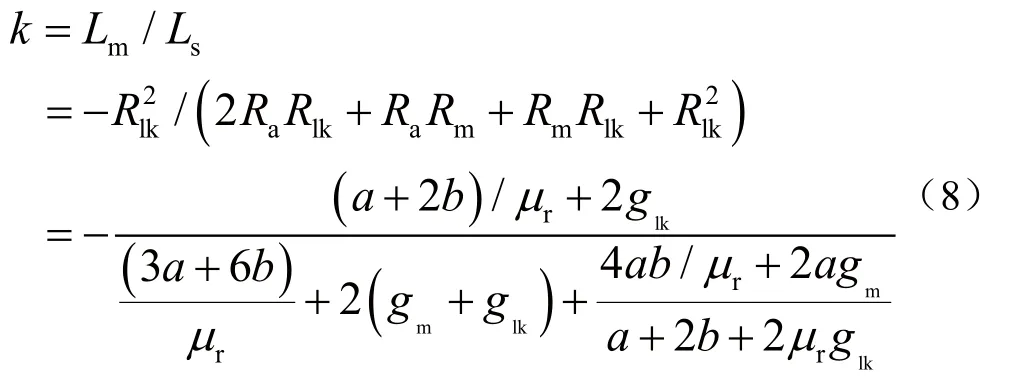
由式(8)可知,通过调整气隙gm、glk的大小,可使耦合系数在(-1,0)范围内变化。
2 耦合系数测量和实验验证
2.1 耦合系数测量
传统耦合电感耦合系数的测量是指测量绕组串联或并联后的等效电感。对于VCC耦合电感,有一种新的耦合系数测量方法,即通过分解耦合电感结构,分别测量自感Ls和漏感Llk的感值,然后根据式(9)求出耦合系数k的表达式为:

其中,反向耦合时,表达式前为负;正向耦合时,表达式前为正。
测量自感Ls和漏感Llk感值的方法如下所述。
自感Ls测量是把耦合电感N2绕组开路,测量N1绕组两端感值,其磁路模型如图5(a)所示,解出此刻所测电感L1感值即为自感Ls的感值,即:
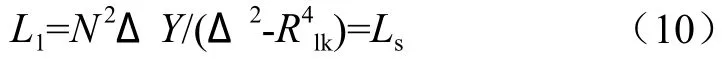
漏感Llk测量是把耦合电感从中间气隙拆成两个独立的电感,测量其中一个电感感值,如1#和3#磁心组成的电感,其磁路模型如图5(b)所示,解出此刻所测电感L2感值即为漏感Llk感值,即:
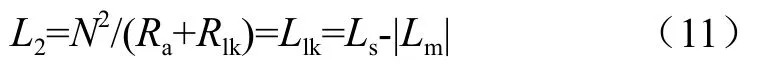
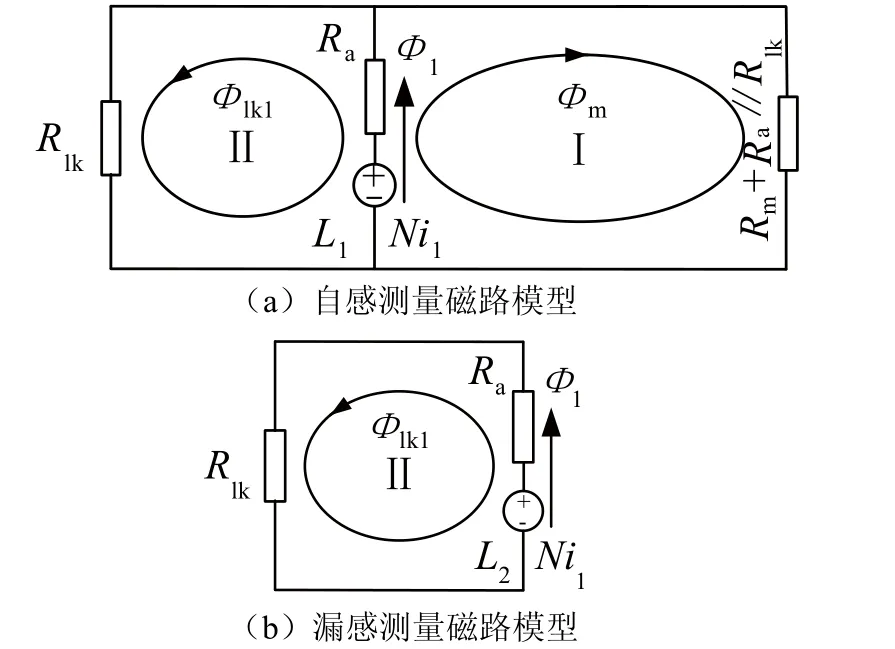
图5 耦合系数测量的磁路模型
2.2 实验验证
本文制作了一个基于UU磁心的VCC耦合电感样机,通过改变气隙大小获得各种耦合系数。电感具体参数为:磁心为新康达公司的UU66/26/20磁心,材质为LP3,磁柱和磁轭长度为45 mm;绕组N1、N2匝数为16;采用GW Instek公司的LCR-829型测试仪测试电感样机参数。该实验只测试分析了耦合系数在-1~-0.5内的大小,实际测试值和理论计算值如表1所示,函数图形如图6所示。分析可知:气隙越大,误差越大,最大绝对误差Δk为0.214 5。由于实验条件有限,气隙控制不精准,造成测量误差较大,但在可接受范围,可认为测试值和计算值吻合较好,从而验证了电感结构的可行性和可变耦合系数原理的正确性。
3 结 论
耦合电感的耦合系数影响多相交错并联磁耦合变换器的稳态性能和暂态性能。针对传统耦合电感的耦合系数不可变的问题,提出了一种基于UU磁心的VCC耦合电感结构。具体地,通过调节磁心气隙得到不同漏感和互感,实现了不同耦合系数;通过分解耦合电感结构测量自感和漏感,找到了一种新的耦合系数测量方法;通过实验样机,验证了VCC耦合电感结构的有效性和耦合系数可变原理的正确性。
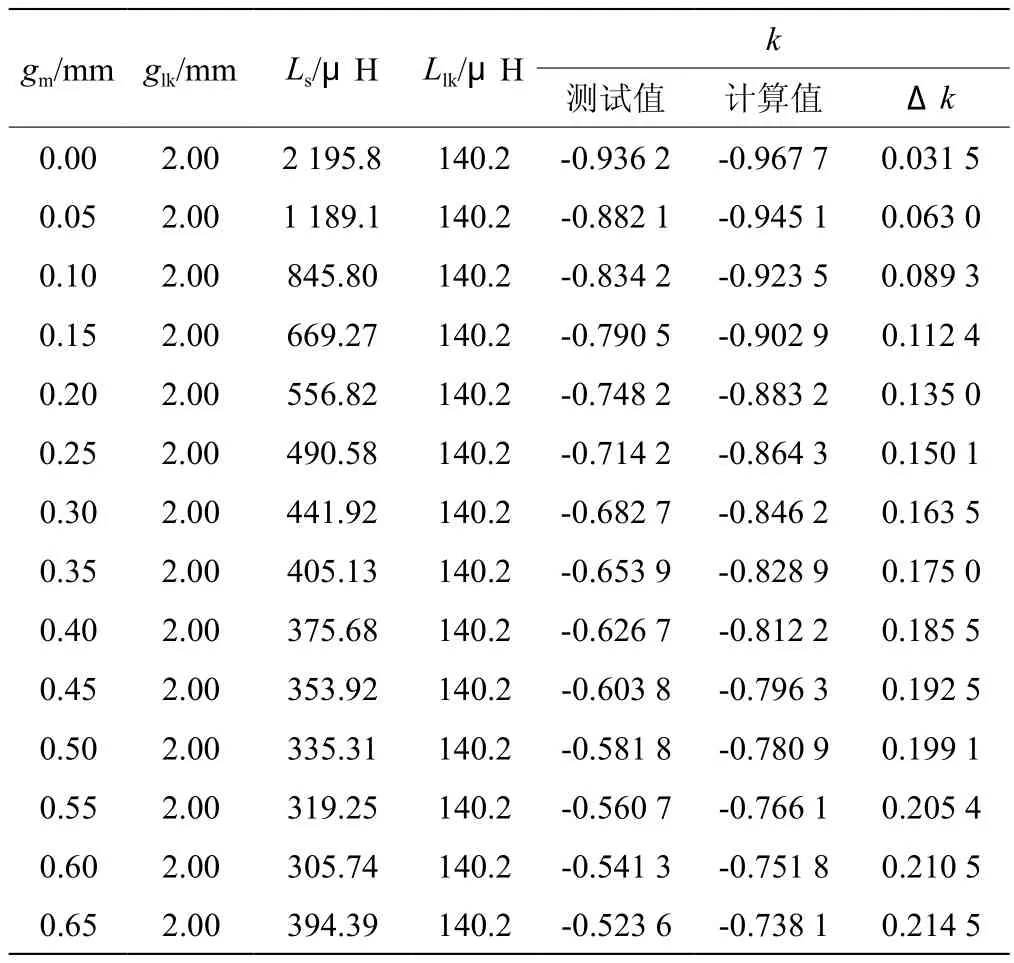
表1 耦合系数的计算值和测试值比较参考文献:
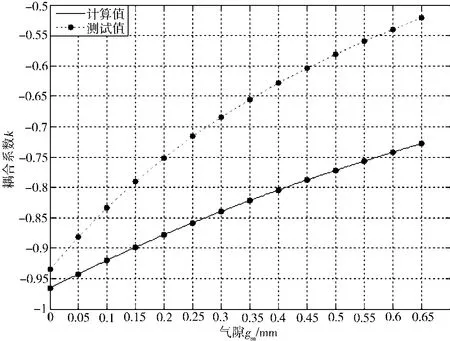
图6 耦合系数函数图形
