一种旋翼轴裂纹扩展寿命分析方法

易政宇，万振华，谢峻岭，宁向荣

（中国航发湖南动力机械研究所，湖南 株洲 412002）

疲劳断裂是直升机旋翼轴失效的主要形式[1]。疲劳断裂主要发生在应力集中部位，经过裂纹形成阶段和裂纹扩展阶段，最终导致彻底失效。裂纹形成阶段是指结构从受载开始到可检测裂纹的出现所经历的过程，裂纹扩展阶段是指出现可检测裂纹后直到构件失稳（或裂纹长度达到给定值）所经历的过程。裂纹形成阶段及裂纹扩展阶段的载荷循环数为构件全寿命。目前国内外普遍采用S-N曲线结合Miner累计损伤法评估零部件安全寿命，但疲劳破坏演化的机理十分复杂，Miner线性疲劳累积损伤理论只能预测疲劳寿命均值，且出于安全考虑其给出的寿命一般为裂纹萌生寿命并非构件使用全寿命[2]。裂纹扩展是结构疲劳断裂的一个重要阶段，从20世纪60年代开始，裂纹扩展研究已成为疲劳强度设计的发展方向之一[3]。

本研究通过有限元仿真技术分析了某旋翼轴的应力分布，确定了疲劳破坏危险部位，建立了旋翼轴裂纹扩展的有限元模型，对裂纹尖端强度因子进行了求解，预测了旋翼轴裂纹扩展寿命，分析了其裂纹扩展特性。最后，通过对旋翼轴故障件进行裂纹扩展仿真分析与寿命计算，验证了该分析方法的可行性。本文为后续的直升机旋翼轴损伤容限设计提供了一种可行的分析方法。

1 基本知识

1.1 裂纹类型

断裂力学是描述疲劳裂纹扩展的理论之一，该理论将断裂的宏观模式分为三个基本型，分别为拉伸张开型、平面滑开型及反平面剪切型(见图1)。旋翼轴工作时受到弯矩、扭矩、剪力、轴向力的交变载荷作用，其疲劳裂纹主要为复合型裂纹。

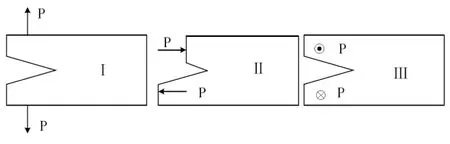
图1 三种基本断裂方式

1.2 应力强度因子（SIF）

应力强度因子是表征外力作用下弹性物体裂纹尖端附近应力场强度的一个重要参量，与裂纹大小、形状以及外应力有关。用应力强度因子来评价裂纹体受力程度，从强度和韧度两方面综合考虑，比单纯用应力作为力学参数更确切、全面。

J K Knowles和E Stenbergn提出的M积分，可用来计算一系列裂纹问题的应力强度因子[4]。M积分又称交互积分(Interaction Integral)，其物理意义是基于面力自由空洞的自相似扩展的能量释放率。本研究利用边界元分析软件FRANC3D(fracture analysis code in 3dimensions)，使用M积分来计算裂纹尖端应力强度因子。

1.3 裂纹扩展速率

Paris给出了裂纹扩展速度da/dN与应力强度因子的关系[5]：

式中：C、n为定值，材料属性由实验测得；a为裂纹长度；N为载荷循环次数；ΔK是应力强度因子幅值，Kmax和Kmin分别对应于最大载荷（或最大正应力）和最小载荷（或最小正应力）的最大和最小应力强度因子。裂纹只有在张开的情况下才能扩展，压缩载荷的作用将使裂纹闭合，因此应力循环的负应力部分对裂纹扩展无贡献，R=σmax/σmin＞0 时，ΔK=Kmax-Kmin，应力比 R≤0 时，ΔK=Kmax。

2 旋翼轴裂纹扩展仿真分析与寿命预测

2.1 有限元模型的建立

首先建立旋翼轴有限元模型。根据国内型号研制经验，旋翼轴受交变载荷的影响，有限元分析建模时，剪力和弯矩按正常工作载荷施加，同时考虑到实际工作过程中轴向力和扭矩存在10%～20%的波动，故轴向力和扭矩以静态载荷的20%作为交变载荷施加。通过有限元分析得到峰值疲劳载荷下构件的应力分布见图2。从图中可以看出，主桨毂下方轴颈处应力最高为300MPa。

根据疲劳理论，破坏一般首先发生在应力集中区域，选择旋翼轴应力较大区域（图2的A、B区）作为裂纹扩展区域，在FRANC3D中建立裂纹扩展子模型，见图3。

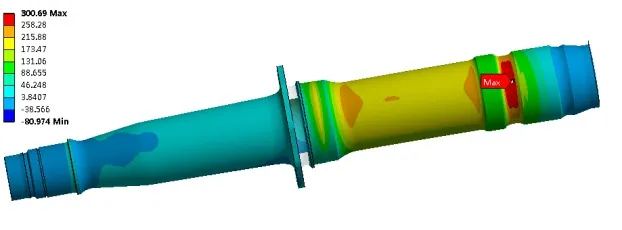
图2 旋翼轴应力分布

图3 旋翼轴裂纹扩展子模型

2.2 裂纹尖端应力强度因子计算

在旋翼轴裂纹扩展子模型的A、B区的内、外表面分别预制半径为1 mm的初始半圆形表面裂纹，见图4。该旋翼轴材料的断裂性能参数[6]（35Cr2Ni4MoA）见表1。

图4 旋翼轴预置裂纹位置

表1 35Cr2Ni4MoA断裂性能数据

A区、B区裂纹扩展分析采用迭代方式进行。分别计算4种位置的初始裂纹情况下，裂纹尖端的应力强度因子，图5示出不同位置初始裂纹情况下裂纹尖端中点处等效应力强度因子Keqv计算结果。FRANC3D软件对等效应力强度因子计算方法如下：

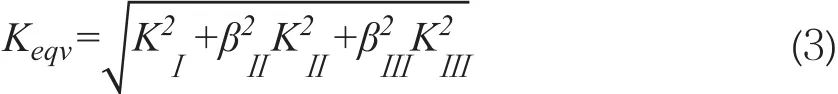
βⅡ、βⅢ为权重因子，旋翼轴裂纹为复合型裂纹，取βⅡ、βⅢ=1。

图5 不同位置初始裂纹情况下裂纹尖端中点等效应力强度因子变化历程

2.3 裂纹扩展寿命预测

由式(1)变换，可以得到：

则裂纹从长度ai扩展到长度ai+1经历的循环数为：

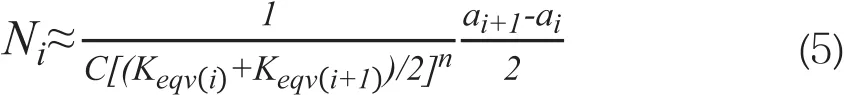
将2.2中计算所得的等效应力强度因子代入(5)式，即可得到裂纹扩展寿命。

不同位置初始裂纹情况下，裂纹长度随循环数变化曲线见图6。不同位置初始裂纹从1mm到贯穿壁厚对应的寿命预测结果见表2。结果显示，旋翼轴初始裂纹在外表面的裂纹扩展寿命要远小于其初始裂纹在内表面的裂纹扩展寿命；旋翼轴初始裂纹在A区外表面的裂纹扩展寿命小于其初始裂纹在B区外表面的裂纹扩展寿命。根据2.1中的应力分析结果，A区应力大于B区应力，外表面应力大于内表面应力。由此说明，该裂纹扩展仿真分析结果与旋翼轴应力分布情况从趋势上看是吻合的。

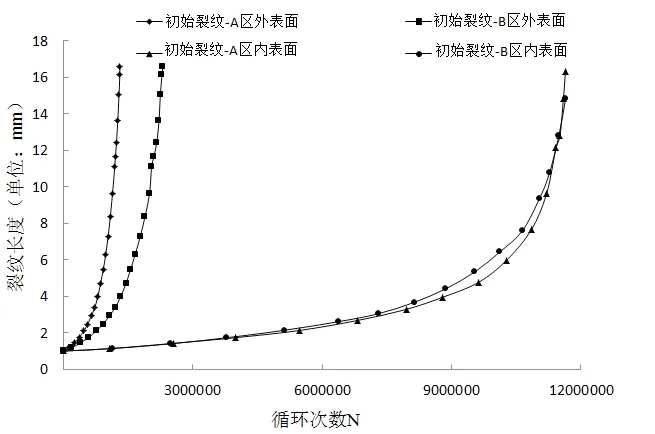
图6 不同位置初始裂纹情况下的a-N曲线

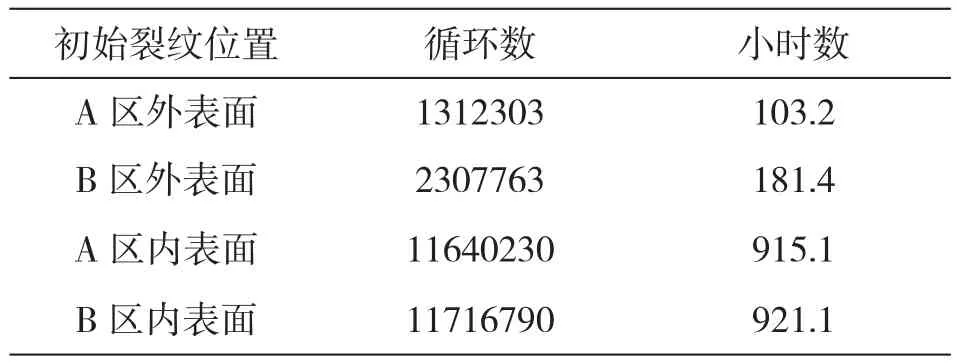
表2 不同位置初始裂纹情况下的裂纹扩展寿命

3 旋翼轴裂纹扩展寿命分析方法验证

3.1 旋翼轴故障件失效分析

某型直升机旋翼轴在仅使用了6小时后外表面出现裂纹，经分解检查发现其裂纹在旋翼轴内孔处沿圆周贯通，在内孔裂纹处发现红色物，断口处有锈蚀现象。该旋翼轴裂纹外部检查情况见图7。

通过对故障件进行失效分析，得出如下结论：

1) 旋翼轴在使用前存在原始裂纹缺陷（热处理裂纹）；2)原始裂纹在使用过程中发生疲劳扩展，贯穿壁厚。

图7 裂纹（外部检查）

3.2 旋翼轴故障件裂纹扩展寿命分析

根据断口分析结果，故障件初始裂纹为深24 mm的斜向裂纹，按此裂纹形貌在旋翼轴裂纹扩展子模型中相应位置植入初始裂纹，见图8。

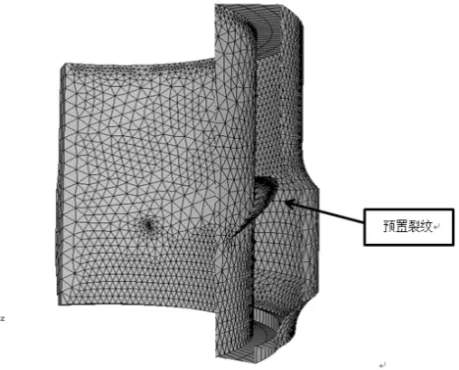
图8 故障件初始裂纹

由于故障件初始裂纹尺寸较大，受边界元分析软件FRANC3D分网规模的限制，须依次植入扩展后的裂纹，并计算裂纹尖端应力强度因子。以0.5 mm为裂纹扩展步长，经过17次计算，裂纹尖端中点处等效应力强度因子变化历程见图9。

故障件裂纹从初始至贯穿壁厚经历的循环数为58884，经转换得出故障件裂纹扩展寿命为4.63小时，其裂纹长度随循环数变化曲线见图10。故障件裂纹扩展仿真分析结果与其实际工作时间（6小时）较吻合。由此说明，故障件是由于带有较大初始裂纹，在一定的工作载荷下裂纹短时间内发生扩展导致，该失效模式与仿真分析结果相符。

4 结论

图9 故障件裂纹尖端中点等效应力强度因子变化历程

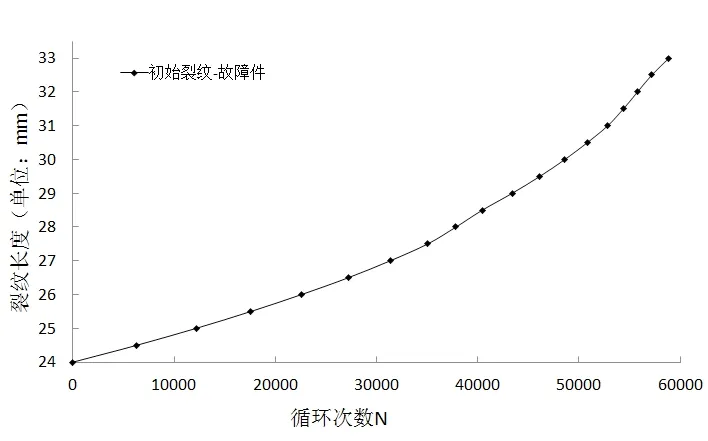
图10 故障件a-N曲线

本研究分析了工作载荷下旋翼轴的应力分布，建立了旋翼轴裂纹扩展有限元模型，在此基础上，计算了裂纹尖端等效应力强度因子历程，根据Paris公式对旋翼轴裂纹扩展寿命进行了预测。研究结果显示，旋翼轴外表面裂纹扩展寿命相对于其内表面的明显较短，在大应力区外表面裂纹扩展寿命最短。最后，通过对故障件进行分析，验证了本文方法的可行性。