细长压杆稳定性的数值模拟

2019-03-22谭嘎子马向荣张国涛张智芳

榆林学院学报 2019年2期

高勇，谭嘎子，吴霞，马向荣，张国涛，樊洋，张智芳

(1.榆林学院化学与化工学院，陕西榆林 719000；2. 陕西省低变质煤洁净利用重点实验室，陕西榆林 719000；3.中国石油吐哈油田公司吐鲁番采油厂，新疆鄯善 838202)

工程结构中存在许多的压杆，如内燃机配气机构中的挺杆，磨床中液压装置的活塞杆，桁架结构中的抗压杆等[1]。压杆稳定在工程实践中的重要性尤为突出，特别是在建筑工程领域。2000年10月25日，南京电视台演播中心工程大演播厅舞台工程屋盖在浇筑混凝土过程中，模板支架发生倒塌事故[2]；1907年，加拿大劳伦斯河上的大桥，因压杆失稳，导致整座大桥坍塌等事件[3]。造成这些事故的原因非常多，但其最主要的原因是由于压杆失稳而导致坍塌，因此，研究压杆的稳定性就显得尤为必要，并采取措施提高压杆的稳定性，可以大大减少此类事故的发生。

近年来，对细长压杆也进行了大量的研究[4-7]，研究结果对分析压杆的稳定性、结构优化及性能提供了思路。汪洋等[8]对细长压杆二阶屈曲临界态进行了数值模拟，得出两端铰支二阶屈曲态细长压杆的临界力为一阶屈曲态临界力的3.24倍；黄开志等[9]对考虑轴向均布载荷压杆的稳定性进行了计算，求得了压杆同时承受轴向均布载荷和集中载荷时临界载荷计算的经验公式。于桂杰等[10]研究了压杆稳定的实验方法，应用欧拉法研究临界压力，并且利用实验使学生更加清楚的了解压杆稳定性实验。李丽君等[11]应用ANSYS软件将压杆稳定中欧拉公式知识清晰直观地以图形动画的方式表达出来，并且应用有限元方法研究了不同载荷对压杆的稳定性情况，从而可以有效的弥补实验的不足，拓宽学生的知识面。本文利用理论计算和数值模拟相结合的方法对细长压杆的稳定性进行了研究，分析了工作参数及结构参数对压杆稳定性的影响规律，研究结果对压杆的理论教学具有指导作用，对实际工程中提高压杆稳定具有重要的意义。

1 细长压杆临界压力的理论计算

对于两端铰支，中心受压的细长压杆其临界力可按欧拉公式计算[12]：

(1)

L—压杆的计算长度，m；

μ—两端铰支，μ=1。

本研究中两端铰支的细长压杆长度为318 mm，宽度为20 mm，厚度为1.9 mm。弹性模量为E=206 GPa。经过计算，压杆临界压力的理论值为229N。

2 细长压杆稳定性的数值模拟

屈曲分析主要用来研究结构在特定载荷下的稳定性和确定结构失稳的临界载荷，包括线性屈曲分析和非线性屈曲分析。线性屈曲分析是以特征值为研究对象，以小位移、小应变的线弹性理论为基础，分析中不考虑结构在受载变形过程中结构构形的变化，也就是在外力施加的各个阶段，总是在结构初始的构形上建立平衡方程。当载荷达到某一个临界值的时候，结构构形突然转变到另一个随遇的平衡状态，将其称之为屈曲[13]。

线性屈曲分析方程如下[14]：

([K]+λ[S]{ψ}=0)(2)

式中：[S]—刚度矩阵；λ—屈曲载荷因子；ψ—屈曲模态形状系数。

上式(2)就是在线性屈曲求解中用于求解的方程，在具体的数值分析中，屈曲载荷因子λ由软件的后处理结果直接读出，屈曲临界载荷Pcr = 所施加压力×λ。

2.1 建立几何模型及划分网格

对于细长压杆，一端固定、一段自由时μ=2，两端铰支时μ=1，因此在进行数值模拟时可将其等效为一端固定、一端自由，长度L为原来一半的压杆。由于所研究压杆结构为两端铰支的长方体构件，因此采用自动划分网格法进行网格划分，并进行了网格无关性检验[15]，网格划分结果如图1。

图1 压杆网格划分图

2.2 设置边界条件及施加载荷

对细长压杆一端设置固定端约束，另一端施加100 N、180 N、220 N的压力载荷。

2.3 数值模拟结果及分析

2.3.1 不同载荷作用下压杆的稳定性分析

把施加100 N、180 N、220 N压力载荷时的压杆分别记为1、2、3号压杆，各个载荷下压杆变形云图如图2所示。利用数值分析所得的屈曲载荷因子可求得临界压力，如表1所示。由图2可得，施加不同载荷时，压杆的变形基本相同，最大变形发生在压杆的中间截面，最小变形发生在压杆的两端。由表1可得，施加不同载荷时，所得屈曲载荷因子不同，但其临界压力基本相同，为 229.82N，和理论临界压力229 N相比，误差为0.36%，因此可以认为采用有限元软件分析得出的临界压力与理论临界压力一致。

图2不同载荷作用下压杆变形云图

表1不同载荷作用下压杆屈曲载荷因子及临界压力数值解

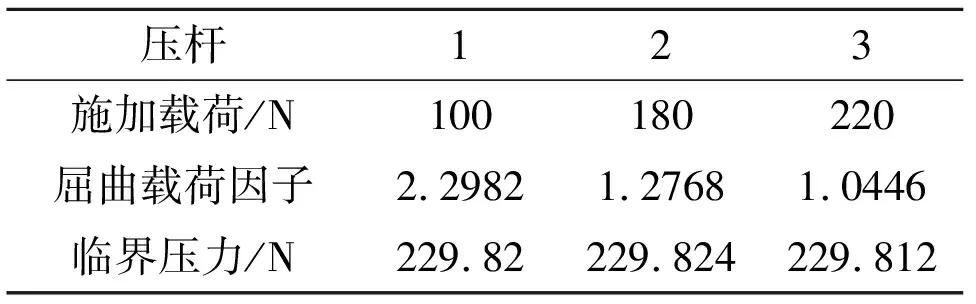
压杆123施加载荷/N100180220屈曲载荷因子2.29821.27681.0446临界压力/N229.82229.824229.812

为了更清晰的观察压杆的失稳情况，分析压杆的六阶模态图，如图3所示。对于中两端铰支的压杆，其两端受到垂直压力的作用，同时压杆会随着垂直压力的值不断增大而逐渐出现弯曲变形，当压力达到临界压力时压杆弯曲变形达到极限，此时的应力值达到最大值，若压杆为塑性材料即认为应力达到屈服极限，若压杆为脆性材料即认为应力达到强度极限，这时的压杆我们就称之为失稳。通过图3压杆的失稳过程就可观察到压杆的失稳情况。当压杆失稳后，对压杆进行卸载，这时的压杆不会恢复原状也就成为不安全构件。

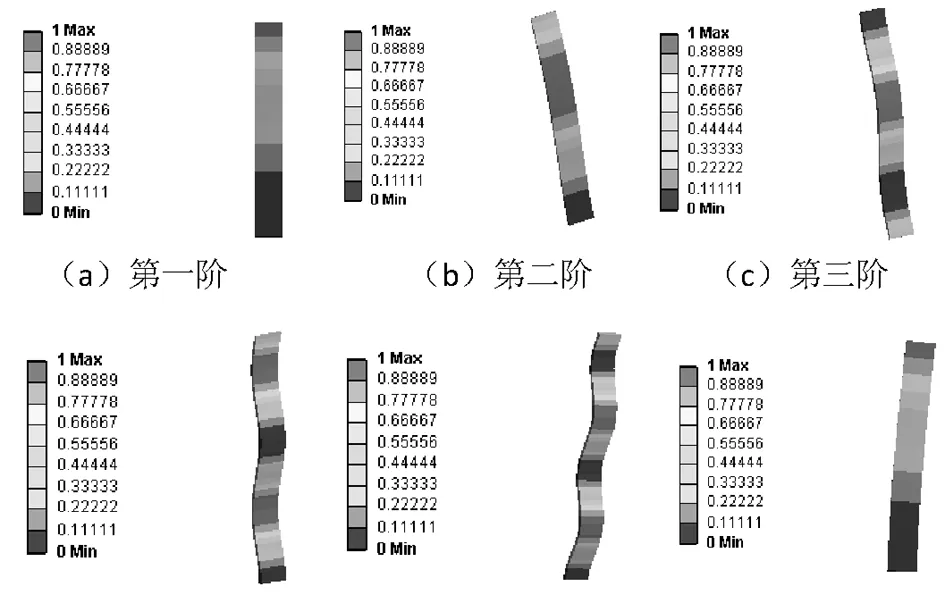
图3压杆六阶模态图

2.3.2 不同弹性模型下压杆的稳定性分析

把弹性模量分别为100 GPa、150 GPa、200GPa、250 GPa的压杆标记为5、6、7、8号压杆，在施加载荷为100N时其屈曲载荷因子和临界载荷数值解如表2所示。

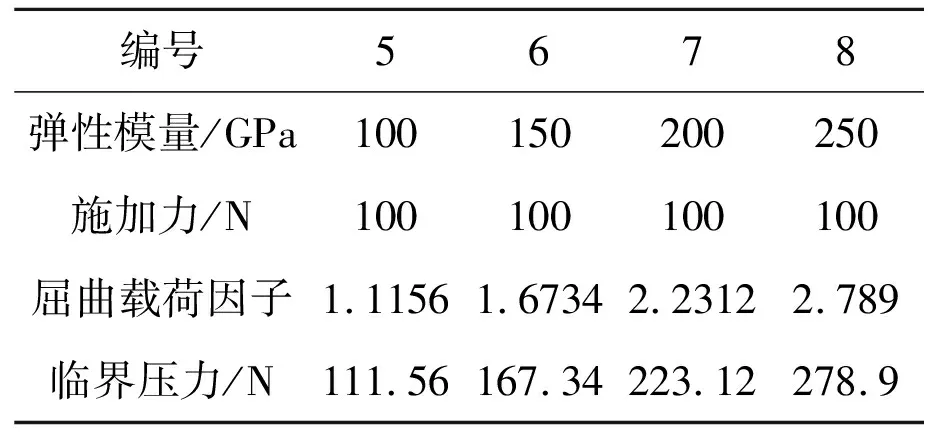
表2 不同弹性模量下压杆载荷系数和临界压力数值解

由表2可得，当压杆在其他条件不变的情况下，材料的弹性模量逐渐增大，压杆的临界压力也逐渐增大，即压杆的稳定性增强。这也正如欧拉公式Pcr=π2EI/(μL)2中所示，压杆的临界压力与材料的弹性模量成正比。因此，在实际工程中为了提高压杆的稳定性，可根据实际情况合理选择压杆的材料。

2.3.3 不同截面面积下压杆的稳定性分析

把宽度分别为10 mm、15 mm、20 mm、25 mm的压杆标记为9、10、11、12号压杆，在施加载荷为100N时其屈曲载荷因子和临界载荷数值解如表3所示。

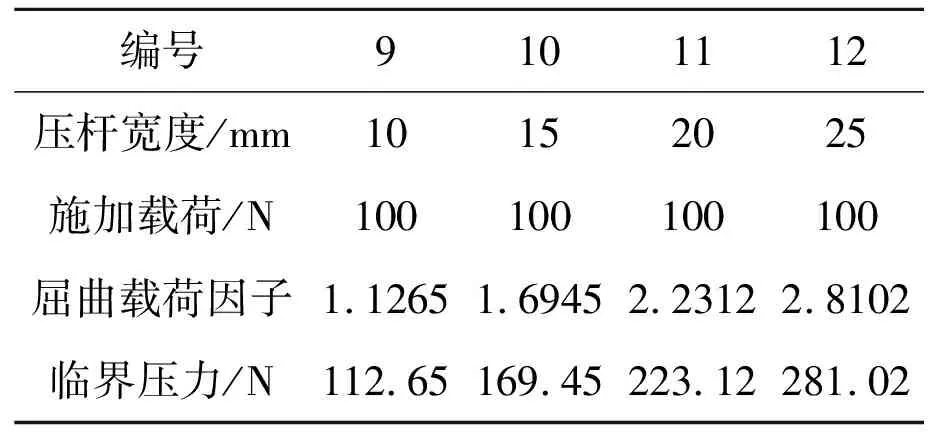
表3 不同截面面积下压杆载荷系数

由表3可得，当压杆在其他条件不变的情况下，压杆的横截面积逐渐增大，压杆的临界载荷也逐渐增大，即压杆的稳定性增强。这也正如欧拉公式Pcr=π2EI/(μL)2中所示，压杆的横截面积增大，则惯性矩I增大，压杆的临界力也随之增大。但是，在选取压杆的横截面时，也不能只为提高压杆的稳定性而将横截面积大大增加，应根据实际情况综合考虑选取一合理值。

通过表2、表3数据的分析，可得知当材料的弹性模量增大以及压杆的横截面积增大时都会增加压杆的临界压力值，即提高了压杆的稳定性。同时利用有限元软件对于提高压杆稳定性的分析与理论分析得出的结果相同。因此，在工程实际中，根据实际要求，利用有限元软件对压杆的稳定性进行分析，并取得一组最优的数据，可以有效地指导压杆的实际应用。