一种基于图像几何矩的非降维连续尺度解构模式
2019-03-22曹地曹建农朱倩
曹地,曹建农,朱倩
(1.长安大学 地球科学与资源学院,西安 710054;2. 国土资源部退化及未利用土地整治工程重点实验室,西安 710054;3. 长安大学 地质工程与测绘学院,西安 710054)
0 引言
人类视觉在多尺度感知机制的驱动下[1],面对一个整体的视觉对象时可以获取该对象不同尺度的视觉信息[2],并捕捉相应尺度下的信息特征。模拟人类视觉的这种多尺度感知机制进行图像处理一直是图像分析研究领域的热点。多尺度图像处理的主要方法是基于降维解构分析,例如,广泛使用的傅立叶变换、Gabor变换、短时傅里叶变换、小波变换[3]、多尺度几何分析[4]、脊波变换Ridgelet、曲波变换Curvelet[5]、轮廓波变换Contourlet[6]、条带波变换Bandelet、楔波变换Wedgelet、小线变换Beamlet、剪切波变换Shearlet[7]等均属此类。虽然维度的降低意味着信息解构会更容易且更完全,但也势必造成高维信息的破碎与损失。因此,非降维解构是图像分析的发展方向之一。
已有少量研究人员致力于非降维结构的图像分析方法研究。A.Cohen、I.Daubechies、R.Q.Jia以及龙瑞麟等对经典小波分析理论进行了高维度推广,但研究进展缓慢,应用则滞于以张量替代真二维[8-10]。二维小波张量的引入,在一定程度上弥补了降维造成的损失,并尝试降低冗余,但这种改善依旧不能突破降维本身制造的上限。如图1所示,多尺度几何分析的发展以及多尺度塔式模型的运用让图像分析向真二维方向发展有了新的迈进。但是目前,相较于降维解构分析发展的完善程度和发展速度来说,非降维的多尺度模型构建方法单一,基础理论不完善,没有系统的评价机制,模型建成后精准尺度筛选依然较少受到关注。
本文基于人类视觉多尺度感知机制,利用经典小波理论以及多尺度几何分析理论中多分辨率的思想,通过塔式模型的建立将非降维的连续尺度图像解构分析引入图像分析的整体过程中。实验表明,连续尺度图像解构分析的加入可以优化图像分割的结果。
1 名词解释
1.1 多尺度
图像的多尺度分析是指图像空间L2(R)中满足单调性、逼近性、伸缩性、平移不变性、Riesz基存在性的一个空间序列{Vj}j∈Z[11]。关玉景等[12]突破了经典多尺度理论的限制,提出了广义多尺度分析的概念。在广义多尺度分析的概念中,允许不同的尺度空间由不同的尺度函数平移伸缩生成[13]。假设L2(R)为一个空间,{Vj}j∈Z为一个空间序列,Vj⊂L2(R),Vj⊂Vj+1,j∈Z,若对每个空间{Vj}j∈Z存在φj(x),使得{φj(x-k/2j)}k∈Z是Vj的标准正交基,则称{Vj}j∈Z是广义多尺度分析。
常见的多尺度构建共有如图2所示的8种模式。在传统塔式模型的构造过程中选择模式f1,如Gaussian Pyramid。模式f1具有计算速度快,迭代衰减速度快,信息认知的整体性高等优势,也是最常用的建模模式。但其劣势也很显著,随着塔式模型的生成,相邻尺度间间隔不断增大,间隔距离呈指数增长。这种模式很有可能导致错失某一应用需求下信息最丰富,应用价值最高的最优尺度,如图3所示。而连续尺度塔式模型f2~f8则可以弥补这一缺憾,同时更加接近人类视觉的多尺度感知机制。f2~f8中,又尤其以f3实现最便捷,运算速度最快,因而本文选用模式f3模式。

图2 多尺度模式

图3 塔式模型
1.2 多尺度分割算法
多尺度分割算法一般依赖于图像经过多尺度解构后产生的不同尺度的图像,各尺度图像独立分割,以各类图像特征作为分割与合并的判别依据,并以权重调控。
本文采用的多尺度分割算法为光谱与形状特征加权的多尺度分型网络演化算法。该算法以多尺度分型网络演化进行分割,并综合采用光谱特征和形状特征,以二者的加权值作为异质性评价准则进行最小异质性合并[14],最终获取分割结果。
(1)
(2)
(3)
(4)
wc代表c维度下权重,n1、n2代表区域面积,h1c、h2c和hmc分别代表合并前相邻区域的异质性和合并后新区域的异质性。光谱特征hspectral采用区域标准差δ表示,形状特征hshape包括光滑度b和紧致度n两个指标。l代表对象边界长度,b代表对象轮廓最小外接矩形的周长,n代表面积,1、2 代表合并前相邻区域的指标,下标m代表合并后指标。综合3种异质性度量指标,合并代价函数为:
f=wspectralhspectral+(l-wspectral)hshape
(5)
hshape=wsmoothhspectral+(l-wsmooth)hcompact
(6)
1.3 矩
矩(moment)的概念来源于数学,在数学统计学中矩被用以描述随机变量的特征,在图像学中矩被用于描述图像的特征[15]。良好的特征不受光照、噪声以及几何形变的干扰。因此在广义多尺度分析的基础上,我们引入图像的几何矩以建立非降维的多尺度图像解构分析模型。
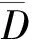
(7)

(8)
中心矩和原点矩的关系:
(9)
归一化中心矩定义为:
(10)
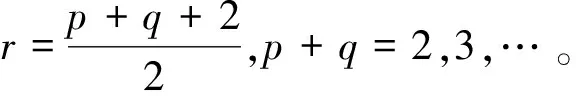
对于图像的矩,阶数越低,对极值越敏感,运算复杂度越低;阶数越高,稳定性越低,且运算复杂度越高。
Hu.M.K首先提出了不变矩的概念[16]。并利用二阶和三阶归一化中心矩构造下面7个不变矩函数式:
φH1=η20+η02
(11)
(12)
φH3=(η30-3η12)2+(η03+3η21)2
(13)
φH4=(η30+η12)2+(η21+η03)2
(14)
φH5=(η30-3η12)(η30+η12)[(η30+η12)2-3(η21+η03)2]+
(3η21-η03)(η21+η03)[3(η30+η12)2-(η21+η03)2]
(15)
(16)
φH7=(3η21-η03)(η30+η12)[(η30+η12)2-3(η21+η03)2]+
(3η12-η30)(η21+η03)[3(η30+η12)2-(η21+η03)2]
(17)
Hu.M.K证明了以上7组矩具有旋转不变性、缩放不变性和平移不变性,是一组高浓缩、高稳定度的图像特征。后续研究证明,在图像识别中,φH1和φH2的不变性保持得比较好,φH3、φH4、φH5、φH6、φH7几个不变矩则由于阶数过高存在一定程度的误差[17]。
矩可以很好捕捉图像特征,且不受光照、噪声以及几何形变干扰,因此本文将以矩作为连续尺度解构模型的基础算子。
2 连续解构模型的构建与分析
2.1 连续解构模型构建
本文针对单通道遥感图像,构造10组独立的解构空间并建立非降维解构模型,10组模型中包括2组基于一阶矩的模型、1组基于二阶矩的模型,以及7组基于由二阶矩与三阶矩组成的不变矩的模型。后对各组模型进行分析。
如表1所示,10组解构空间构造分别基于Ma,Mb,Mc,Md,Me,Mf,Mg,Mh,Mi,Mj,10组图像矩。其中,为降低极值对于低阶矩的干扰,构造b组空间同时对图像进行降噪处理。

表1 解构空间的矩算子
解构模型层级存在自然上限,也可以设置固定值上限,本文设定固定值解构上限为50,即全部10组模型的解构层级N均为50。构造过程采用多尺度模式f3,即解构模型单层窗口大小与层级对应,窗口建立从图像左上角开始,层级间隔一致。对尺度窗口内的图像区域进行矩运算,获取的特征值作为窗口值。
即对于解构模型窗口:
WN={(xn,yn)=MomentN*N,n=1,2,…,N};
(18)
{N:1~50};
{Moment:Ma,Mb,Mc,Md,Me,Mf,Mg,Mh,Mi,Mj}。
10组解构模型如图4所示。
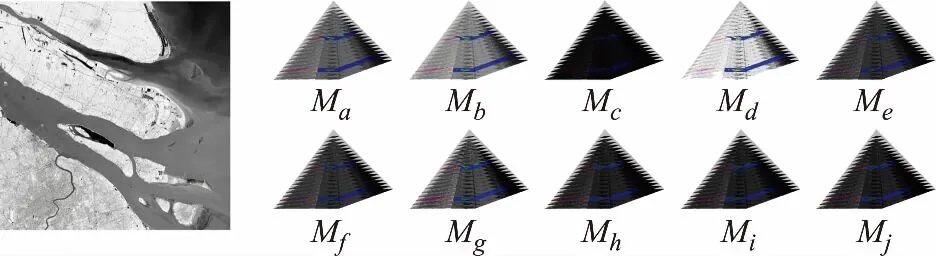
图4 解构模型
2.2 连续解构模型分析
1)统计分析。以上10组解构模型的50层级平均信息量统计结果显示,在这10组空间中,信息量分布呈现两种模式:均衡模式与增长模式。如表2所示。

表2 信息量分布模式
呈现均衡模式的模型,平均信息量在层级间变化不明显,无显著上升或下降趋势;呈现增长模式的模型,平均信息量在相邻层级间存在突变,整体呈现缓慢上升趋势(图5)。

图5 平均信息量统计图
2)纵剖面分析。如图6所示,在连续解构空间的纵剖面中,即同一解构空间的不同尺度下,呈现均衡模式的三组解构空间Ma,Mb,Md,其信息分布状态相近,且随着尺度增大,信息分布变化趋势相近,波峰无明显位移;呈现增长模式的7组解构空间Mc,Me,Mf,Mg,Mh,Mi,Mj,其信息分布状态相近,且随着尺度增大,信息分布变化趋势也相近,波峰随尺度变化右移。相较于均衡模式,增长模式下的解构空间信息变化规律更明显,衰减速度更快,整体稳定度更高。
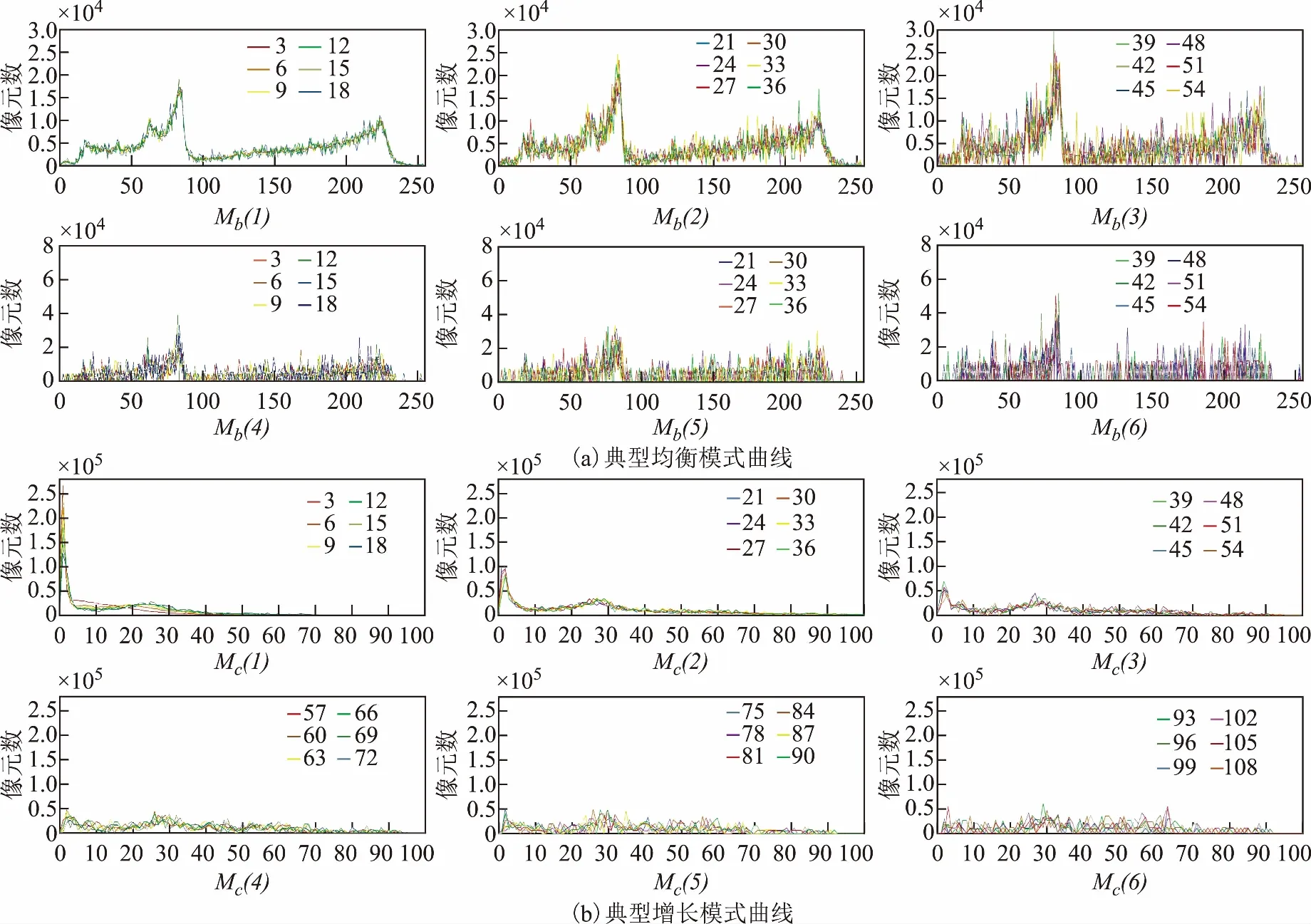
图6 连续解构模型纵剖面
3)横剖面分析。如图7所示,在连续解构空间的横剖面中,即不同解构空间的同一尺度下,均衡模式与增长模式的解构结果同样存在明显分异。如图,呈现均衡模式的解构空间对于细节信息更敏感,更适合于细节信息获取,而呈现增长模式的解构空间对于边缘信息更敏感,更适合用于边缘提取与图像分割,但几何矩阶数过高会使解构结果破碎,整体可用性降低。
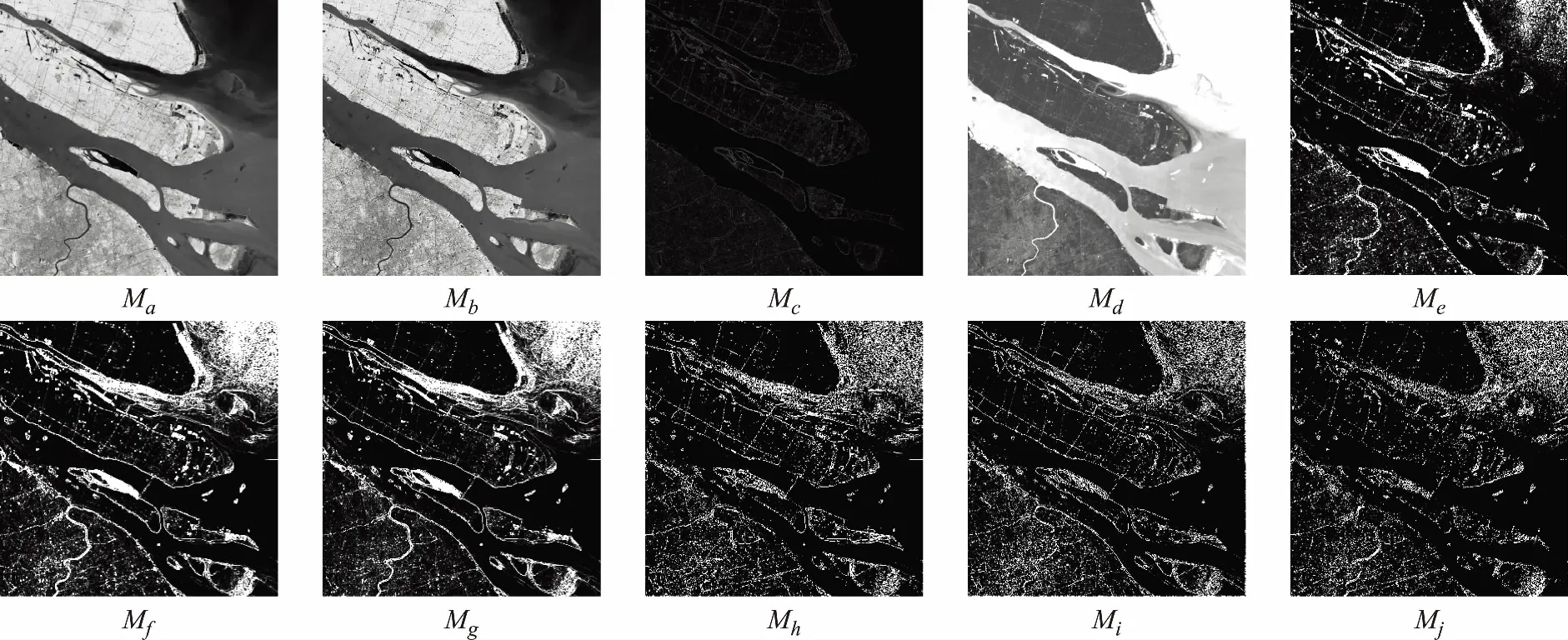
图7 连续解构模型横剖面
3 验证
将解构模型代入光谱与形状特征加权的多尺度分型网络演化分割算法验证。验证对象为均衡模式解构空间组和增长模式解构空间组。验证区间为解构空间的第6~20层级,共15级。分割过程中,多尺度组合模式为原始图像叠加相应层级,所有图层权重一致,参数设定一致。
作为对照组,将未解构的原始图像分别代入多尺度分割算法、分水岭分割算法和四叉树分割算法进行分割。分割结果如图8、图9所示。
熵值是体现混乱程度的度量。在信息量位于同一量级的前提下,熵值也在同一量级,此时熵值越低信息混乱程度越低。

图8 多尺度分割

图9 对照组
如图10所示:(1)3组算法中,相较于分水岭算法与四叉树算法,多尺度分割算法本身存在优势;(2)多尺度算法下,相较于空白对照组,加入解构信息后的2组分割结果信息混乱程度都更低,分割效果更佳;(3)对比均衡模式解构空间和增长模式解构空间的分割结果。二者在分割结果上存在明显差异,后者在所有层级上信息混乱程度均更低,即增长模式解构空间提供的多尺度信息更有利于图像分割。但同时二者存在一致性,即均在第8层级体现出最优分割结果。
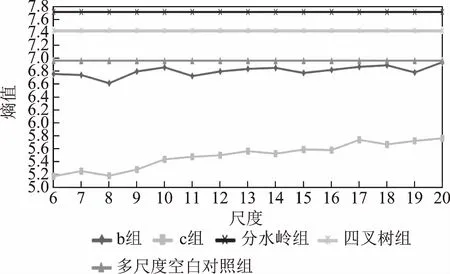
图10 熵值图
提取第8层级分割结果进行进一步对比(图11)。对原始图像标定100个对照检测点位,对照加入。均衡模式下,有效点位为60%;增长模式下,有效点位为72%。同为有效点位,增长模式下,优势点位更多。

图11 第8层级点位检测
4 结论
本文建立了一种基于图像几何矩的非降维连续尺度解构模式,并在此模式下构建了10组非降维解构模型。分析显示这些模型呈现均衡模式和增长模式两种形态。代入多尺度分割算法验证结果证明:本文所提出的非降维连续解构分析方法可以提升多尺度分割的效果,且增长模式下的解构信息对于图像分割更有利。
