双树复小波域马尔科夫的遥感图像分割方法

汪汇兵，范奎奎，欧阳斯达，戚凯丽，杨朦朦

(1.自然资源部国土卫星遥感应用中心，北京 100048；2.中国矿业大学，江苏 徐州 221000；3.山东科技大学，山东 青岛 266510)

0 引言

遥感图像分割作为信息提取、地物分类与特征识别的重要环节，是遥感图像处理技术研究的热点和难点之一[1-3]。随着遥感图像空间分辨率的不断提高，纹理细节信息越来越丰富，地表覆盖愈加复杂多样，像素空间相关性愈发复杂，影像灰度、噪声等不确定性增加，一方面对遥感图像分割在区域细节信息上的精度要求越来越高，另一方面灰度不均、噪声、地物边缘混叠等现象对分割的影响越来越大。

聚类方法作为常用的基于像元的图像分割算法，是根据图像像元灰度的不同将图像内的各像素划分到预先设定的几种不同类别中，然后将属于同一类别且相互连通的像素合并为同一个区域[4-6]，具有算法实现简单，迭代收敛速度快的特点。常用的聚类方法包括有K均值(K-means)[7-9]，模糊C均值(fuzzy C-means，FCM)[10-12]，期望最大化法(expectation-maximization，EM)[13]等，但此类方法都只是在单一尺度上进行，且没有考虑像素与邻域之间的关系，对于具有复杂信息的高分辨率遥感图像的分割，易受噪声、地物边界混叠和灰度不均匀的影响，且易丢失目标的细节信息，引起误分割问题，分割细节精度和鲁棒性欠佳。

由于马尔科夫随机场(Markov random field，MRF)模型具有能够很好刻画图像信息的空间相关性并能有效建立上下文的先验模型的特性，基于MRF模型的分割算法已经广泛应用于图像分割中[14-15]，以解决传统聚类方法存在的问题。文献[16]结合分数阶微分理论提出了一种MRF纹理图像分割模型，并通过对比试验验证了基于MRF的分割方法能够较好弥补FCM法仅利用灰度信息，对像素空间信息描述不完善的缺陷。文献[17]提出了一种基于模糊马尔可夫随机场的无监督遥感图像分割算法，结合FCM的模糊性和MRF的空间相关性，并考虑图像的灰度特征和纹理特征，使分割结果更加准确，但是这类方法任只在单一尺度上进行，对于图像的边缘、细节及突变信息表达较弱，而且难以较好地克服影像噪声的影响。

而小波分解具有多尺度分析特性，基于小波分解的多尺度分割算法[18]，可以提升分割的边缘精度与细节表达。文献[19]提出了一种基于小波变换的多分辨率图像分割方法，将小波的多尺度分析与形态学方法相结合较好地减少图像过分割现象。文献[20]提出了一种带有边界的小波域Markov模型图像分割算法，并通过对医学图像的试验，证实了它不仅能有效地区分不同区域，而且可以很好地保留边界信息。文献[21]将双树复小波变换(dual-tree complex wavelet transform，DT-CWT)与MRF模型相结合对纹理图像和遥感图像进行分割，由于DT-CWT具有逼近的移不变性、更多的方向选择性和完全重构的性质，进一步提高了基于离散小波与MRF分割算法的分割精度，但这类方法忽略了高分辨率遥感图像的不确定性，对于图像的模糊问题，如地物边界混叠，灰度不均匀等分割效果不佳，且未考虑图像噪声对分割的影响。文献[22]提出了一种基于DT-CWT的模糊聚类分割方法，在DT-CWT域内利用改进的FCM分割算法对纹理图像及航片进行分割，利用DT-CWT较好地提高了FCM分割算法的边缘准确性、区域一致性和分割精度，同时利用FCM的模糊性在分割中较好地处理了地物边缘的混叠，明显减少了斑点噪声，但是这类方法都是在假设像素独立的前提下进行的，并未考虑像素间的相关性，边缘分割粗糙，误分像素较多。

为了提高分割方法的细节精度和鲁棒性，综合考虑图像分割的多尺度性、模糊性及像素的空间相关性，本文结合双树复小波变换DT-CWT的多尺度和多分辨率特性、模糊马尔科夫随机场(fuzzy Markov random field，FMRF)模型中FCM的模糊性以及MRF的像素空间相关性，提出了一种非监督遥感图像分割方法，简称为DTCWT-FMRF。该方法首先采用DT-CWT对图像进行多尺度分解，准确表达高分辨率遥感图像的细节信息，并利用贝叶斯(Bayesian)阈值对高频分量进行滤波处理，进一步去噪和突显细节信息，提高方法的抗噪性。然后为了避免由于不同层分量的尺寸不同引起分割边缘的模糊，重构处理后的相应层高、低频分量，并充分考虑图像分割的模糊性和像素邻域间的相关性，在FCM初始分割下建立MRF模型，再根据最大后验概率准则(maximum a posterior，MAP)实现各层的最优分割。最后根据相似度融合规则融合各层分割结果，进一步提高分割细节精度，得到最终的分割结果。并通过与多种常用的聚类方法分割结果进行定量比较，分析算法的优缺点。

2 DT-CWT和FMRF分割模型

2.1 DT-CWT分解

DT-CWT是将复小波实部和虚部的生成分开来实现，是通过两组并行的实数滤波器组来分别获取复小波的实部变换系数和虚部变换系数。DT-CWT不仅继承了传统离散小波变换(discrete wavelet transform，DWT)良好的时频分析能力，最主要的是具有近似的平移不变性和更多的方向选择性，以及弥补了复小波不能完全重构的缺陷[23]。为了克服奇/偶(odd/even)滤波器因严格线性相位引起的采样结构差异的缺点，本文采用Kingsbury提出的基于正交变换的(quarter sample shift，Q-Shift)滤波器组[24]对图像进行DT-CWT分解，每层分解可得到1个低频子带和6个方向(±15°，±45°，±75°)的高频子带。如图1所示为三层DT-CWT分解示意图，其中X为原始图像，X(n)(n=1，2，3)为第n层分解的高、低频子带。图中阴影部分为低频子带，空白部分为高频子带。

图1 三层DT-CWT分解树状图

2.2 FMRF图像分割模型

(1)

(2)

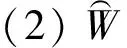
argmaxP(W=w|F=f)∝
argmin(U(w)+U(w，f))

(3)

式中：U(w)为标记场能量，U(w，f)为特征场能量。从公式(3)可以看出，最终的能量大小由标记场能量和特征场能量共同决定的。由于 ICM易收敛到局部能量最优解，分割效果依赖初始标记场状态[27]，本文采用FCM聚类算法对ICM的初始标记场进行模糊化。

3 结合DT-CWT和FMRF的图像分割算法

3.1 算法流程

综合考虑高分辨率遥感图像的尺度层次、算法复杂度，本文选择进行3层DT-CWT分解和FMRF结合进行试验，算法流程图见图2所示。

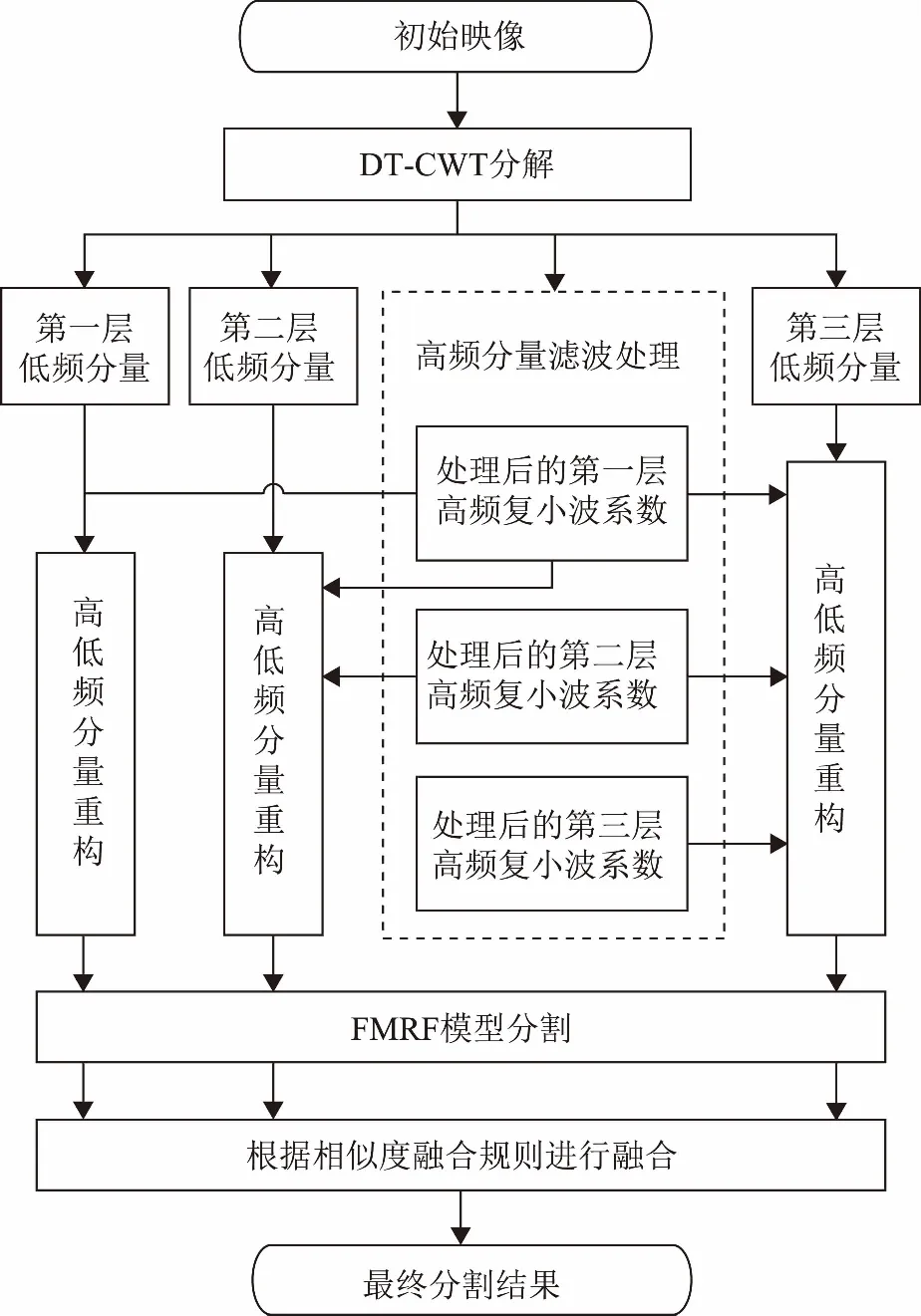
图2 基于DT-CWT和FMRF的图像分割流程图

假设X是待分割的遥感图像对应的灰度矩阵，具体算法实现步骤如下：

步骤1对X进行三层DT-CWT分解，每层分解可分别得到1个低频子带记为{L1，L2，L3}带和6个方向的高频子带记为Hk，l，(k=1，2，3；l=±15°，±45°，±75°)；

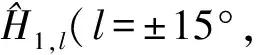
步骤4分别对C1、C2、C3进行基于自适应Bayesian阈值的 FCM初始分割，得到初始分割状态，为W1、W2、W3；

步骤5基于MRF与GRF的等价性，利用ICM迭代模型不断迭代更新分割状态，达到最终的最优分割Z1、Z2、Z3；

步骤6根据定义的相似度融合规则，对Z1、Z2、Z3进行融合，即得到最终分割结果Z。

算法中，FCM循环终止条件选择为相邻两次循环聚类中心差值均小于0.000 1，最大迭代次数为15次，ICM最大迭代次数设置为30次。

3.2 高频分量处理

经过三层尺度分解后，遥感图像分解的各层低频分量承载着图像的亮度或灰度变化缓慢的区域信息，描述了图像的主要能量；而各层高频分量承载图像的突变信息，如图像边缘、轮廓信息及大部分噪声信息。为了平衡高分辨率遥感图像分割中噪声的去除和高频细节信息较好地保留，在3.1节步骤2中，

首先对高频复小波系数的实部和虚部分别进行Bayesian阈值滤波处理，然后将各层处理后的实部和虚部对应相加组合成复小波系数来实现。具体算法实现示意图如图3所示。

图3 高频分量处理过程示意图

以印度尼西亚英德地区Landsat-8卫星影像为例，图4为经过DT-CWT分解得到的第一层复高频子带图像，从左到右分别表示-75°、-45°、-15°、15°、45°、75°方向的高频信息；图5为经过Bayesian阈值滤波处理后的第一层复高频子带图像。可以看出经过Bayesian阈值滤波处理后的高频分量，杂点更少，能量更加集中。

图4 第一层复高频子带图像

图5 经Bayesian阈值滤波处理后的第一层复高频子带图像

3.3 FMRF分割模型

由文献[27]可知MRF分割中的ICM迭代易收敛到局部能量最优解，分割效果非常依赖初始分割条件，通常选择K-means分割算法作为图像的初始分割方法。但经过归一化后进行DT-CWT分解得到的各高、低频子带系数都很小，由灰度直方图来确定K-means初始聚类中心不仅困难，且效果不佳。故本文采用FMRF分割模型，即用FCM聚类算法对图像进行初始分割，并由Bayesian阈值确定初始聚类中心，不仅解决了高分辨遥感图像的聚类中心确定困难问题，而且可以避免K-means的硬分割问题。

假设待分割图像灰度矩阵为X(i，j)，设定聚类数为3且只考虑二阶邻域系统，FMRF的ICM迭代算法具体步骤如下：

步骤1对X(i，j)求取Bayesian阈值level1将X(i，j)分为两类，并对方差较大的类再次求Bayesian阈值level2，然后根据v1=(min(D(i，j))+min(level1，level2))/2，v2=(level1+level2)/2，v3=(max(D(i，j))+max(level1+level2))/2求取初始聚类中心V=[v1，v2，v3]；

步骤2计算FCM的隶属度矩阵U，并根据U更新标记场Wm和聚类中心Vm，其中m为迭代次数；

步骤3设定迭代总次数，重复步骤2不断对标记场Wm进行迭代更新；

步骤6判断循环终止条件(迭代终止条件设置为30次)，重复步骤4、5不断对标记场进行迭代更新，达到最终的MAP最优分割。

如图6为经过上述基于FMRF模型得到的3个分割结果，对应3.1节步骤5中的Z1、Z2、Z3。

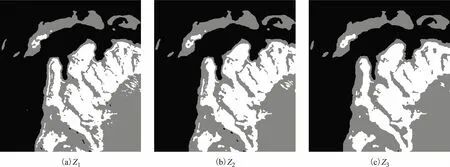
图6 基于FMRF模型分割的三层结果

3.4 相似度融合规则

为了弥补因取交集引起的细节类别漏分现象，本文根据自定义的相似度融合规则进行融合。

首先，定义u为相似度，为了最大程度保留高分辨遥感图像的细节信息，统计二阶邻域内与目标像素值相同的数目，记s个相同像素值，则相似度u=s，其中(0≤s≤8)且为整数。

相似度融合规则即是，统计3.1步骤5中Z1、Z2与Z3中二阶邻域内对应位置的像素的相似度u1、u2和u3，并根据u1、u2和u3的大小来确定最终划分的类别，具体规则如下：比较分割结果Z1、Z2与Z3中对应位置的像素值，若Z1(i，j)=Z2(i，j)=Z3(i，j)，则使Z(i，j)=Z1(i，j)；否则若u1=max(u1，u2，u3)，使Z(i，j)=Z1(i，j)；若u2=max(u1，u2，u3)，则使Z(i，j)=Z2(i，j)；若u3=max(u1，u2，u3)，使Z(i，j)=Z3(i，j)，具体相似度融合规则实现流程图如图7所示。

图7 融合规则示意图

4 试验与分析

为了检验所提算法的分割细节精度和鲁棒性，分别选用传统的K-means法[7]、FCM法[11]、MRF法[15]与文中所提方法DTCWT-FMRF法进行试验和对比分析，所有算法运行环境均为Intel(R)Core(TM)i7，2.67 GHz主频，8 GB内存，Matlab2012a。试验图像如图8(a)为2014年9月30日辽宁省金州区的ZY-3卫星影像，裁剪尺寸均为384×384，图9(a)为2013年8月3日印度尼西亚英德地区Landsat-8影像，裁剪尺寸均为382×352，图8(b)和图9(b)分别为其对应的参考分割图像，是通过直接观察原始图像灰度差异和结合人工阈值分割结果手动提取出来的。如图10和图11分别为对应影像各种方法的分割结果。

图8 辽宁省金州区ZY-3卫星影像

图9 印度尼西亚英德地区Landsat-8影像

图10 辽宁省金州区影像的各种算法分割结果

图11 印度尼西亚英德地区的各种算法分割结果

由图10和图11可以明显看出K-means法和FCM法分割比较分散，杂点较多，而且明显存在过分割现象；MRF法方法分割杂点较少，但是边缘分割参差不齐，较为粗糙；相比之下可以看出本文所提方法分割呈块状，杂点最少，边缘分割较为平滑，表现出区域一致性，视觉效果较好，这是由于在本文算法中进行了双树复小波变换，较好地克服了传感器噪声和配准误差的影响，并通过FMRF进行分割，充分考虑了高分辨率遥感影像分割的模糊性和像素间的相关性，使得分割结果表现出较好的区域一致性。

由于通常情况下，高分辨率遥感图像噪声表现为孤立的离散点，没有空间关联性，故可视为服从高斯分布[28-29]，为了更直观验证本文所提方法对高分辨遥感图像分割的鲁棒性，对带有高斯噪声的仿真图像进行试验，如图12是根据高分辨率遥感图像特性并加入方差为0.005的高斯噪声的仿真图像，大小为192×192，图13为仿真图像分割结果。可以明显看出，对于含有噪声的仿真图像，本文所提方法分割较为充分，且不含杂点，去噪效果明显。

图12 带有高斯噪声的仿真图像

图13 4种方法仿真图像分割结果

为了进行客观评价，表1给出了真实影像和仿真图像的各种方法分割结果的评价指标值，包括：总误分像素数(overall error，OE)、正确率(overall right，OR)，以及运行时间T。设标准分割为R(i，j)，算法分割结果为Z(i，j)，图像总像素数为n，各评价指标的计算式为：

OE=sum(R(i，j)≠Z(i，j))

(5)

(6)

式中：T为各算法变化检测实际运行时间。

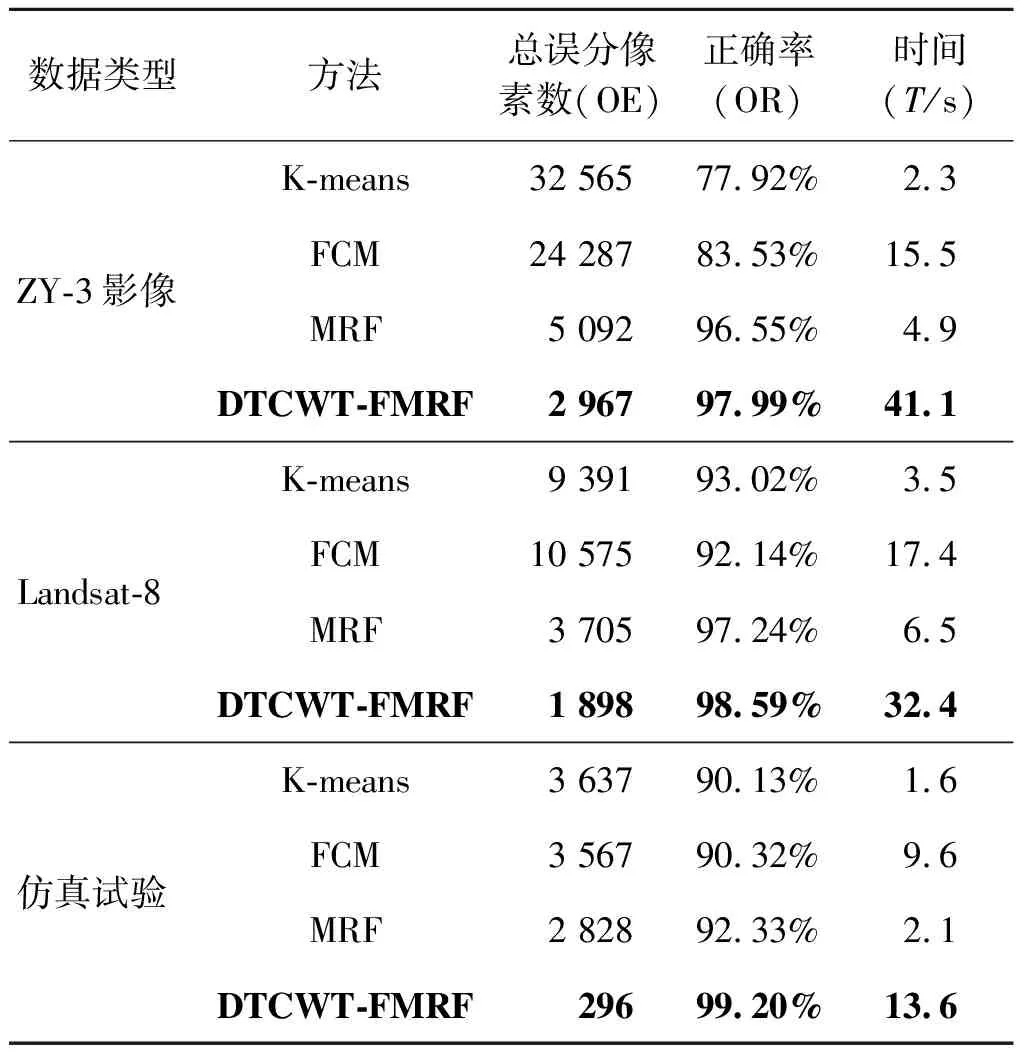
表1 4种算法分割结果性能比较

从表1可以看出，3组图像分割试验中聚类方法K-means 和FCM的OE相当且明显高于基于MRF分割的方法，说明将MRF的空间像素相关性引入到高分辨率遥感图像分割中可以大大降低像素误分现象；另外可以看出DTCWT-FMRF法的OE最小，OR最大，说明将DT-CWT的多尺度表达特性与FCM模糊性、MRF的像素空间相关性相结合可以明显提高影像分割精度；但从算法耗时上看，所提方法耗时最长，这是由于算法中存在DTCWT域高频信息处理和FMRF分割模型中的多次循环迭代过程的缘故。因此以牺牲算法耗时为代价前提下，本文所提方法较传统的K-means法、FCM法及MRF法在性能指标总误分像素数、正确率上表现最优。

综合主、客观可以看出，在不考虑算法耗时情况下，本文所提方法边缘分割更加平滑细腻，区域一致性更好，具有较好的视觉效果，同时能够很好地抑制噪声，具有较高的分割精度和较强的鲁棒性。

5 结束语

本文提出了一种基于DT-CWT与FMRF模型相结合的非监督高分辨率遥感图像分割算法，首先利用DT-CWT的多方向表达性、各向异性和多尺度特性对原始图像进行多尺度分解，有助于高分辨遥感图像细节信息的表达与分析，提高了分割精度；然后通过Bayesian阈值法对各高频子带进行去噪并重构相应层的高、低频分量，较好地平衡了噪声的去除和高频信息的保留；最后利用基于FCM分割的ICM迭代算法对重构的各层信息进行分割，并根据所提出的相似度规则融合各层分割结果得到最终的分割结果，充分考虑了像素分割的模糊性和像素邻域间的相关性，不仅大大降低了误分率，而且能够很好地去除杂点和噪声的影响。对比试验结果表明：基于DT-CWT与FMRF相结合的分割方法较其他3种常用聚类分割方法杂点分割较少，边缘分割更加平滑细腻，且总错误数最小，正确率最高，具有较高的分割细节精度和较强的鲁棒性，更适合高分辨率遥感图像分割。由于算法中存在多次迭代过程，耗时较长分割效率较低，对于更高分辨率的图像分割处理能力有待提升，对于如何提高算法分割效率和算法复杂度分析需要进一步的研究。