桥梁上部结构碰撞的破坏模式与载荷计算技术研究

叶 琳

(阳光学院 土木工程学院，福州 350015)

近年来，为解决城市交通拥堵问题，立交桥等形式的立体交通建设模式正在被广泛应用于城市建设中。国内建设的桥梁均采用统一标准设计。随着运输行业的不断发展，大型重卡货车比例增多，为了实现效益最大化，货车的载重量及所载货物高度远远超出额定范围。因此，国内外近年来因车辆超高等问题而引发的桥梁上部结构破坏问题屡见不鲜[1]。相关资料显示，如今国内在正在通行的桥梁，因高度超标准导致近2成桥梁受到车辆碰撞而损坏的现象。在国外，以美国为例，约有6成桥梁上部受到超高车辆不同程度的撞击[2]。

为解决车辆碰撞问题，一方面需要进行交通运行规范化管理；另一方面也需要从桥梁的设计结构和防碰撞能力入手，从根本上解决由于交通工具超高而导致的桥梁碰撞和损坏问题。随着有限元仿真分析技术的不断创新，根据实际场景对碰撞情况进行仿真分析，可以有效实现场景再现和预判，提升设计的安全性和可靠性。本文基于有限元方法，对桥梁上部结构碰撞的破坏模式以及计算技术进行研究，提出超高车辆在碰撞情况下的计算方法，为桥梁结构设计提供参考依据。

2 车辆碰撞桥梁有限元模型

超高车辆碰撞桥梁的模型包含两部分：一是车辆模型，二是桥梁模型。

2.1 车辆模型

本文采用国际通用的2轴标准卡车模型[3-4]，有限元模型的三视图如表1所示。卡车模型的相关尺寸信息如表1所示。摩擦系数和摩擦力计算方法选择和文献[4]相同的方法。

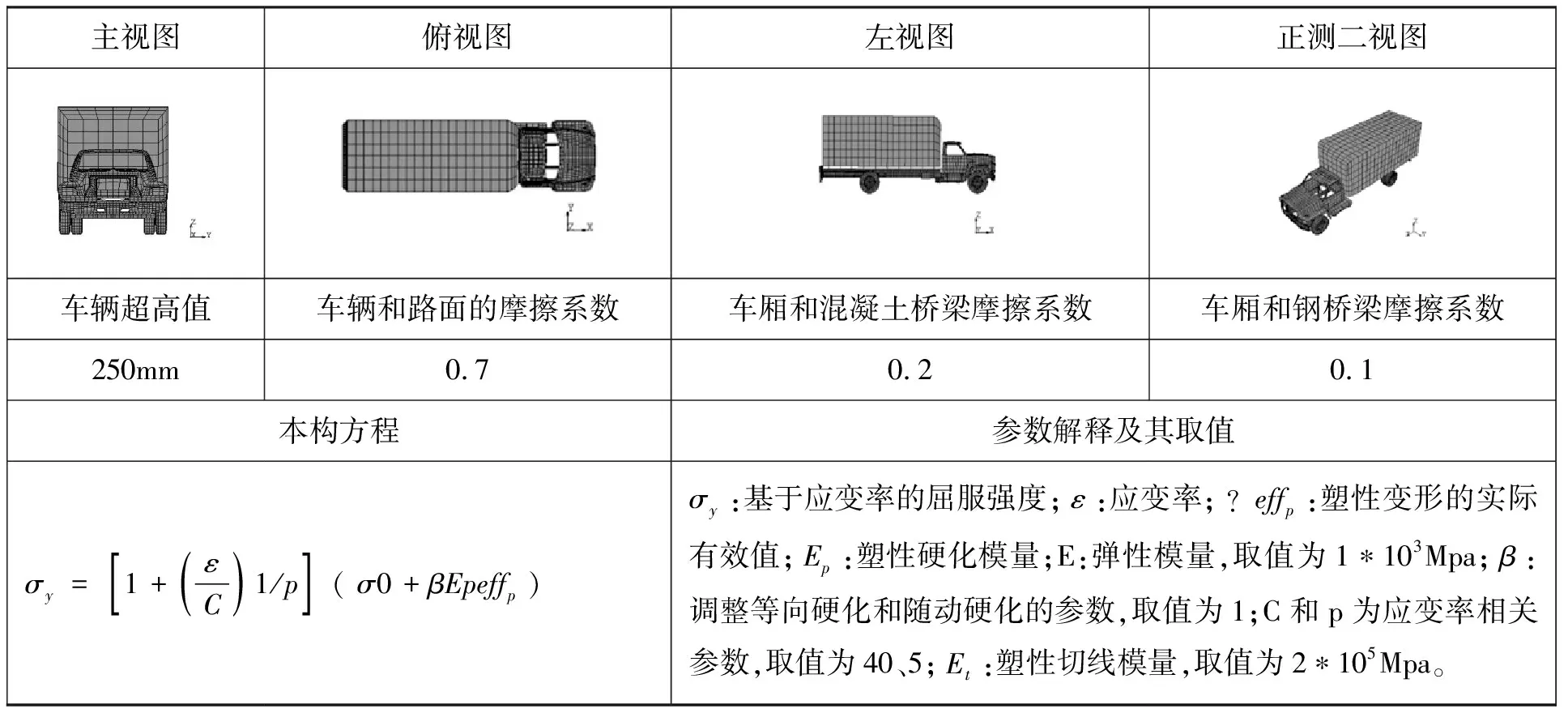
表1 标准卡车有限元模型视图及参数

2.2 桥梁上部结构模型

本文选择了基于MSC.MARC的仿真软件作为桥梁上部结构模型的搭建平台。基于实体模型构建混凝土单元，再使用其已有的钢筋单元进行钢筋模拟。混凝土所受拉力和压力分别比阿勇弹塑性和弥散裂缝模型仿真，其他详细参数见相关文献[5]。所建立模型的相关尺寸信息如图1所示，仿真模型如图2所示。桥梁为双车道简支梁类型，其整体跨度为25m，宽度为6.1m，中间含有3根T型混凝土梁。在桥梁的两段各放置有250×450×60的材质为橡胶的固定支座。对于T型支架筋及桥梁其他力学性能信息如表2所示。桥梁上部有限元模型的质量为185t。

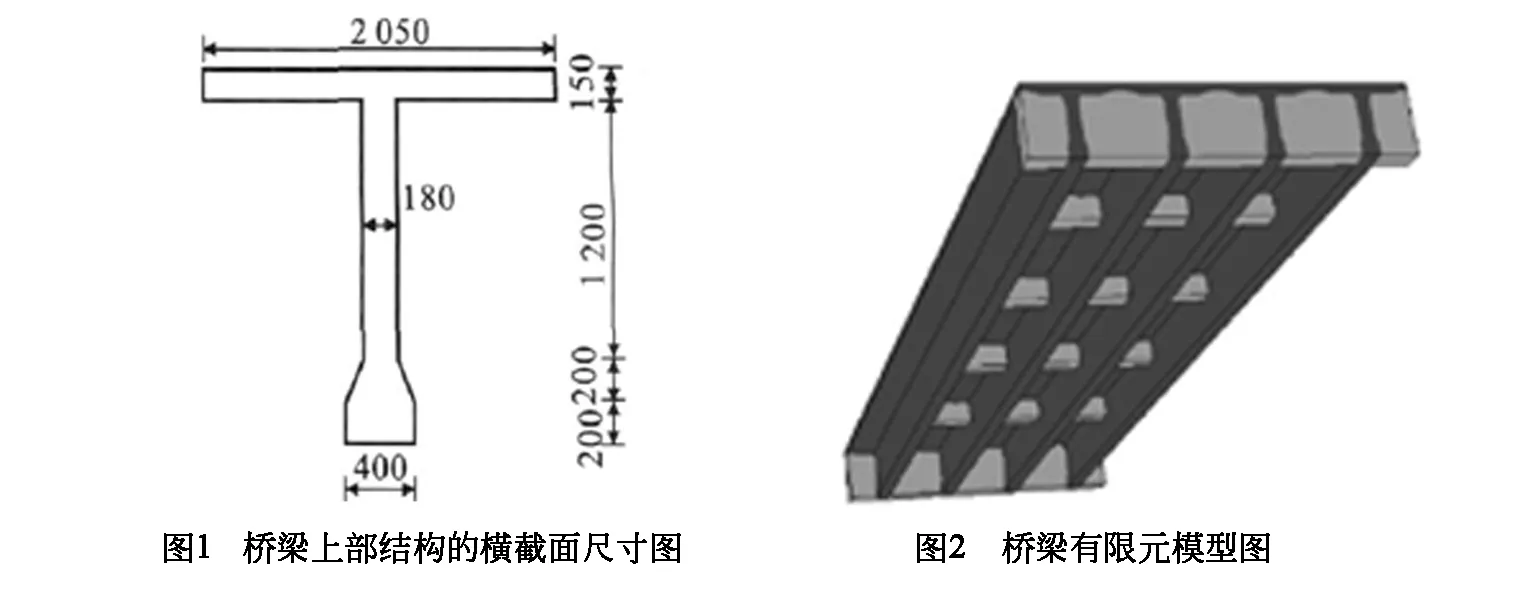
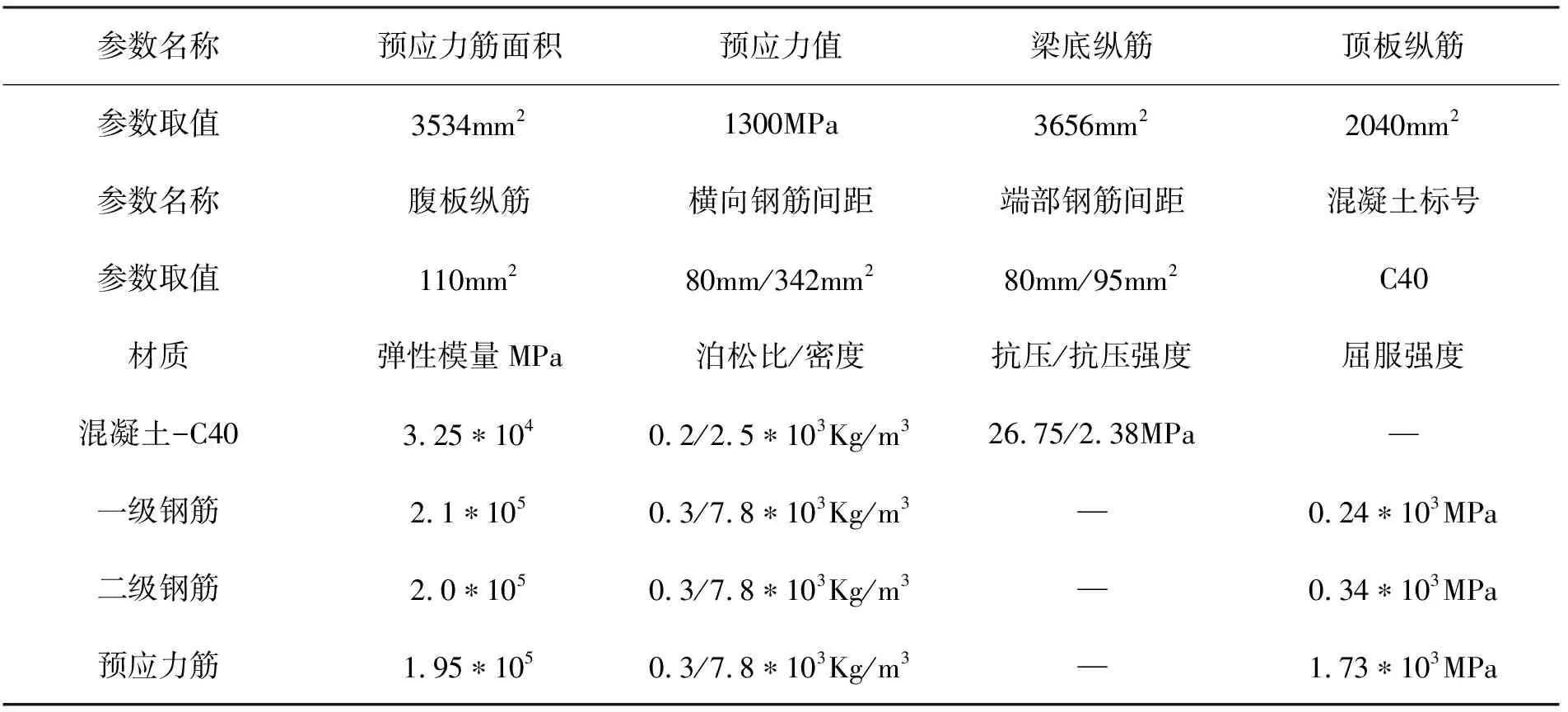
表2 T型支架筋及桥梁其他力学性能

2.3 有限元模型网格划分及验证

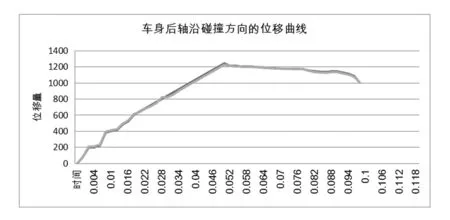
图2 车身后轴沿碰撞方向的位移曲线

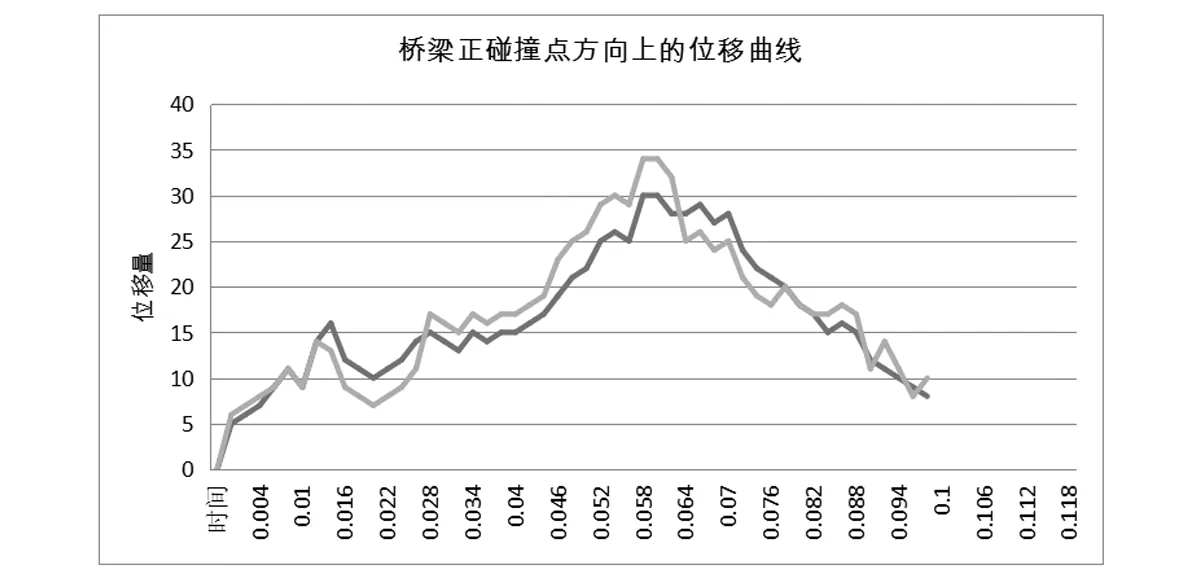
图3 桥梁正碰撞点方向上的位移曲线

有限元仿真中网格划分的正确与否是影响仿真结果的重要因素。为了验证网格划分的密度和收敛特性，本文对桥梁上部结构采用线弹性模型，作为仿真的本构模型。相关计算结果如图2和3所示。从图2可以看出，两种场景(车身后轴的碰撞方向位移曲线)本仿真实验网格划分网格密度，对车以及桥梁的形状变化产生的影响很小，说明网格划分在密度和精度上已经达到了相关要求。

2.4 工况分析

为保证仿真结果的准确性，本文根据实际碰撞场景，虚拟出各种碰撞工况，并将碰撞点设置在桥的正中点处，如图5所示。本文仅考虑水平约束力，没有考虑垂直约束力作用。水平约束力分为摩擦力、橡胶支座的弹力、固定支座的固定约束力三种情况。为了验证跨及车道数量参数对最终结果影响的大小，本文分析了单跨、三跨，双车道和四车道几种工况。同时，选择了不同的车辆行驶速度分析碰撞结果。所有仿真工况如表3所示。

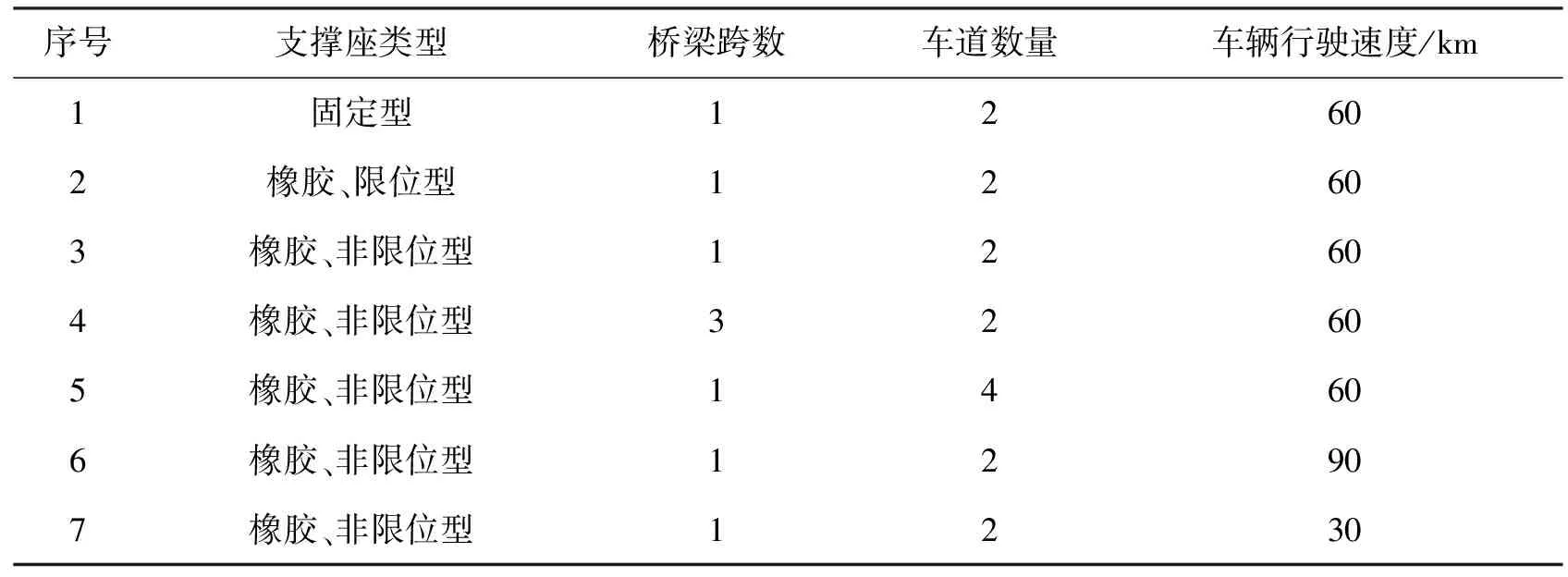
表3 不同工况详细参数介绍

3 破坏模式分析

3.1 基本破坏模式

桥梁受到车辆撞击后，其变形和位移的方式一般分为三种，即绕固定轴的转动、弯曲变形和刚体的水平转动和纵向弯曲。根据以上三种变形和位移方式以及有限元分析结果，对桥梁的破坏模式进行分析。桥梁的破坏模式包括整体损坏和局部损坏两种情况。本文所分析桥梁的支架类型为T型，其局部破坏形式可以分为碰撞接触位置混凝土的局部裂缝和脱落如图4所示，腹与面板相连接处混凝土的裂纹如见图5所示。根据相关事故分析报告可知，由于车辆高度过高导致的撞击桥梁现象，也会造成较为严重的局部破坏，如图6所示。

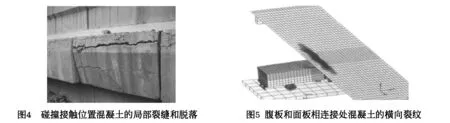
图6 撞击造成的局部变形现象

当撞击发生后，若位移超过一定程度，则会发生整体破坏现象。桥梁的整体变形可以分为三种，即扭转型、落梁破坏和弯曲破坏。以上三种整体破坏会发生在碰撞瞬间，也可能发生在碰撞动作完成以后，例如落梁破坏和弯曲破坏现象，具体如图7和图8所示。

图7 落梁破坏有限元分析示意图 图8 弯曲破坏现象事故现场图

3.2 破坏机理分析

导致破坏的主要原因是有害位移。根据各类变形识别出来的有害位移分析可知，桥梁刚体的水平运动、绕轴向的扭曲变形、水平弯曲三类是主要的有害位移。对前三类碰撞场景的有害位移量进行了对比分析如图9所示。从图中可以看出，工况1发生弯曲和扭曲破坏的概率最大，而发生落梁破坏的概率较小。限位支座的使用可以有效防止落梁破坏现象的发生，但水平方向上的扭转和弯曲破坏，两者没有太大差异。在以上三种工况下，发生弯曲破坏有害位移的概率基本一致。

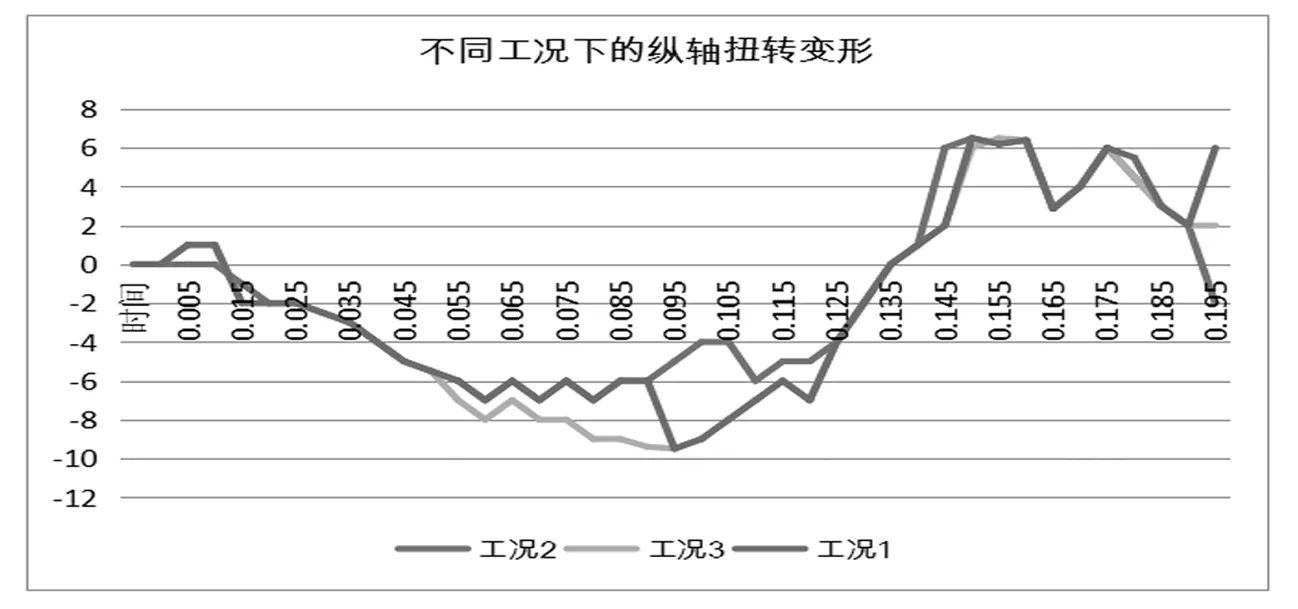
图9 不同工况下绕纵轴扭转变形趋势图

4 载荷计算

4.1 支架形式和桥梁跨数对碰撞力的影响研究

为研究支架形式对碰撞力的影响，本文以前三个工况为研究对象，分别对其不同工况下水平碰撞力和纵向碰撞力的变化趋势进行了研究，结果如图10和图11所示。

从图10中可以看出，三种工况下其碰撞力变化趋势均是一致的，并且力的大小方面差异也不大，说明支座类型对碰撞载荷的影响是比较小的。其原因是由于在碰撞发生时，卡车的质量和桥梁上部的质量差异较大，桥梁上部的变形会比卡车的变形量小。从图11也可以看出，支座类型对纵向和水平碰撞力的影响是一致的。本文还分析了桥梁的跨数对碰撞力的影响，同样得出结论，桥梁的跨数对碰撞力的变化趋势影响也比较小，跨数为3跨或者1跨，其水平和纵向碰撞力的变化趋势均是一致的，数值上差异不大。以下所有图中所示碰撞力的单位均为MN。

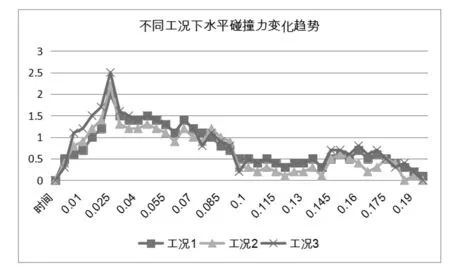
图10 不同工况下水平碰撞力变化趋势图

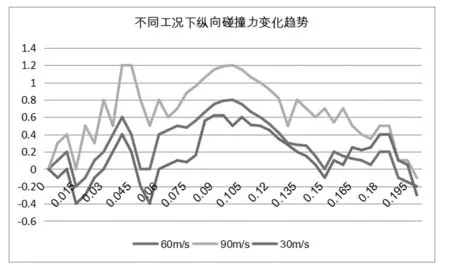
图11 不同工况下水平碰撞力变化趋势图

4.2 车初始速度对碰撞力的影响研究

本文选择5、6、7为实验工况，监测了碰撞力大小，并绘制了碰撞力变化趋势图，如图12所示。工况5、6、7的碰撞初始速度分别为60m/s、90m/s、30m/s。由图12可知，不同速度下，水平碰撞力变化趋势虽然一致，但是其差距较大，从90m/s-30m/s碰撞力依次减小。用同样的方法对其纵向变化碰撞力进行了分析比较，也得出相同的结论。碰撞的初始速度和碰撞的载荷大小是呈现正相关的关系，速度越大，桥梁碰撞点所承受的载荷越大。由此认为，碰撞的动量(即速度和质量的乘积)是造成桥梁受损的主要因素。

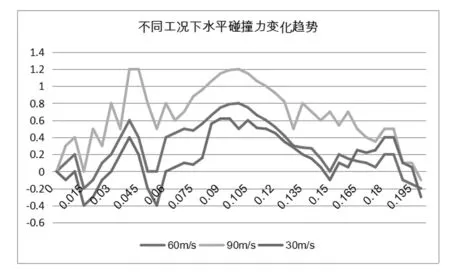
图12 卡车初始速度对碰撞力的影响

4.3 碰撞载荷的决定要素分析

为了进一步验证动量是造成桥梁在与卡车碰撞瞬间产生载荷的主要要素，对不同工况下水平和纵向冲量数值进行了计算，计算结果如表4所示。

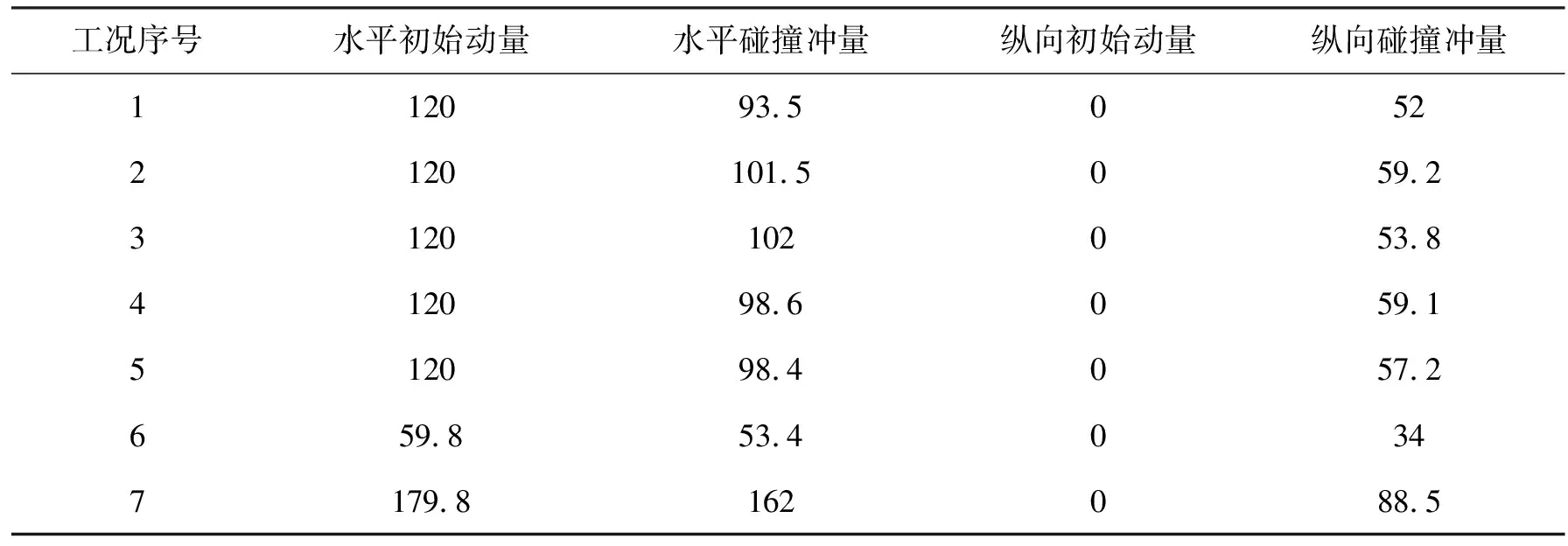
表4 碰撞过程中冲量值大小

从表中可以看出，桥梁在碰撞瞬间所承受的碰撞力与支座的形式和桥梁的跨数关系较小。因此，仅研究车辆的相关属性，即可准确计算碰撞过程中碰撞冲量的大小。本文对碰撞力发生的持续时间进行合理简化，并得到碰撞过程中速度和冲量的线性回归函数关系式。水平、纵向上的碰撞速度和碰撞冲量的关系为标准的一次函数关系，水平方向的函数关系式为Y= 1.6X+8；纵向碰撞冲量和速度函数关系式为Y=X-5。

为了提出切实可行的工程设计载荷量计算方法，进一步简化了碰撞力确定模型。除车辆相关属性外，碰撞力大小还与桥梁以上的位移量、破坏模式相关。本文对桥梁上部整体破坏和位移响应，简化为碰撞力的形式计算，对局部类型的破坏采用碰撞力时程*M(M为局部动力放大系数，取其值为2)。假设水平和纵向碰撞的持续时间为0.1s和0.15s，取碰撞初始速度为60m/s，选择1为研究工况，最终测得产生的水平反力、扭转和弯曲变形力与实际有限元计算结果对比图，如图13所示。

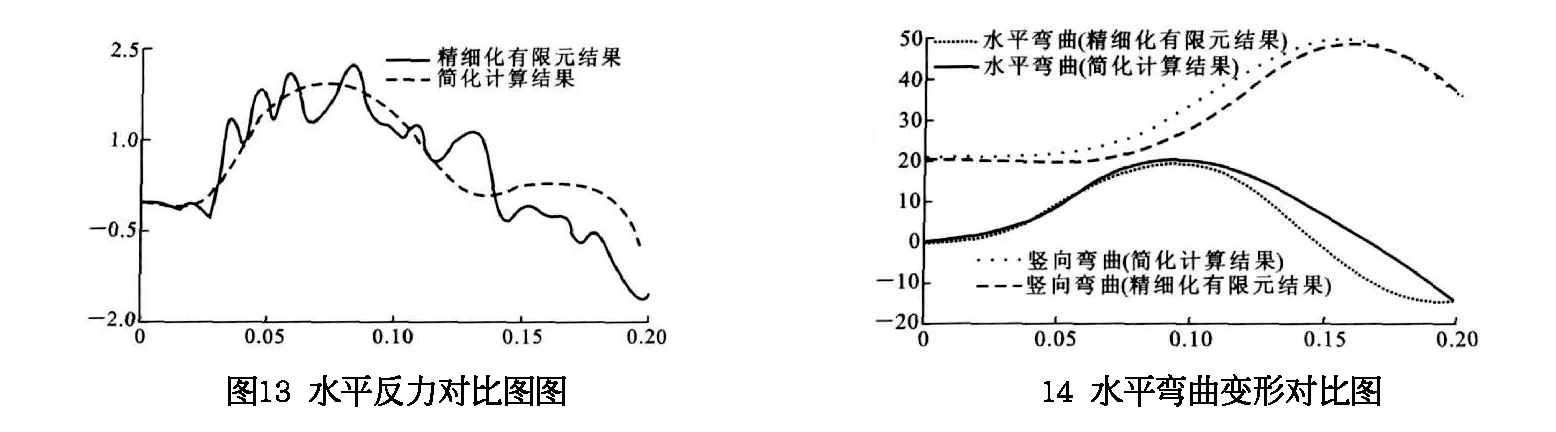
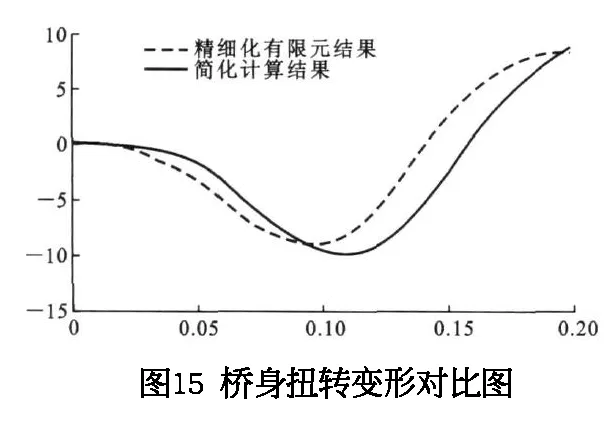
由以上3图可知，简化模型和精细化模型的计算结果基本一致。经过试验，所计算的简化模型和精细化模型能够满足精度要求。

5 结语

本文研究了桥梁上部结构碰撞破坏模式和载荷的计算方法，得出如下结论：

(1)本文所建立的车辆碰撞桥梁上部有限元模型，为工程设计提供了有利的仿真模型支撑。

(2)通过对破坏机理分析和对碰撞过程中桥梁所承受的载荷计算，得出在碰撞过程中，支座类型、桥梁结构、跨数对碰撞力的影响不大。车辆的质量、碰撞时卡车的初始速度、位移的量及破坏模式对桥梁碰撞过程中载荷具有重要影响作用。

(3)本文提出的速度和冲量的模型关系以及有限元的载荷计算方法，为工程设计提供了有利的模型支撑，可作为工程设计载荷计算的有效工具。