帽形滑环式组合密封的密封性能研究*

(西南石油大学机电工程学院 四川成都 610500)

王宣银[1]对聚四氟乙烯组合密封圈的特性进行了分析，并推导了其摩擦阻力的计算公式。谭晶等人[2-3]利用有限元方法，对方形同轴密封件(格来圈)、阶梯形同轴密封件(斯特圈)在不同参数下的密封性能进行了研究。张欢等人[4]对运用于汽车起重机支腿油缸的DAS组合密封圈密封特性进行了研究。刘清友等[5]对C形滑环式组合密封进行了研究，分析了结构参数与运动参数对密封性能的影响。陈家旺等[6]通过仿真得到了齿形滑环组合密封的摩擦力矩计算值，并通过实验对其进行了验证。王嘉毅等[7]建立了叶片式摆动缸组合密封的理论计算模型，并通过实验验证了其模型的合理性。NIKA和SAYLES[8]对复合矩形往复密封进行了建模，分析了接触力、油膜厚度、泄漏、动摩擦等参数，并对结构进行了优化。HU等[9]利用有限元仿真对自补偿同轴斜锥滑环组合密封性能进行了研究，证明了其自补偿性能的有效性。

综上可知，目前对于组合密封的研究主要集中在密封性能、密封原理、密封特点、密封主控因素等方面，且当前的研究主要针对C形、齿形、复合矩形组合密封等密封形式，尚未发现有相关文献对帽形滑环式组合密封的密封性能进行系统研究。因此，本文作者从帽形滑环式组合密封原理出发，基于ABAQUS建立帽形滑环的二维轴对称模型，分别研究在静密封和动密封条件下，工作压力、密封间隙、运动速度、摩擦因数等参数对于密封性能的影响，为帽形滑环式组合密封的设计与应用提供借鉴与参考。

1 帽形滑环式组合密封的密封原理

如图1所示，帽形滑环组合密封是由帽形的增强聚四氟乙烯(PTFE,Polytetrafluoroethylene)滑环与O形橡胶圈组合而成的[10]。在运动过程中，增强PTFE材质的滑环与运动部件直接接触，由于增强PTFE滑环具有耐磨性强、摩擦因数低的特点，同时由于O形橡胶圈能够提供弹性力，从而可保证整个密封系统持续可靠。

图1 帽形滑环式组合密封示意图

采用帽形滑环式组合密封大大降低了系统的摩擦力，能够有效地消除运动部件在低速时的爬行现象，防止O形橡胶圈在运动过程中发生缠绕，有效减少摩擦发热引起的密封失效等问题。帽形滑环式密封具有较高的可靠性，特别适用于轻型低摩擦液压与气动设备。

2 模型建立

2.1 基本假设

由于O形圈橡胶具有高度的非线性，因此，在研究过程中对橡胶作如下基本假设：(1)材料的拉伸特性与压缩蠕变性质相同；(2)材料性质均是各向同性材料；(3)约束边界的指定位移会使密封圈受到纵向压缩；(4)忽略温度对橡胶参数的影响。

2.2 材料本构模型

橡胶是不可压缩的各向同性的超弹性材料，通常使用应变能密度方程来描述它的本构模型[11]。在研究的帽形滑环式组合密封中，O形橡胶圈采用丁腈橡胶(NBR，Nitrile Rubber)，该材料是不可压缩的各向同性的超弹性材料。对于应变能密度方程，各向同性超弹性材料可以表示成Cauchy-Green变形张量C的3个不变量的函数，即:

W=W(Ic,IIc,IIIc)

(1)

Rivlin将应变能密度函数表示成Ic和IIc的级数展开式：

(2)

式中：Cij是力学性能常数。

尽管高阶的多项式模型可以精确地模拟超弹性材料的应力-应变关系，但需要确定多个常数，这些常数的确定往往比较困难。特别是在实验数据有限的情况下，很难得到有效的高阶常数。

当保留式(2)中的前两项，得到不可压缩橡胶材料的Mooney-Rivlin模型的表达式为

WMR=C10(Ic-3)+C01(IIc-3)

(3)

式中:C10和C01为力学性能常数。

根据相关文献，采用的丁腈橡胶材料参数分别为C10=1.87 MPa,C01=0.47 MPa[12]。

2.3 有限元前处理

在ABAQUS中建立二维轴对称模型，包括缸体、活塞杆、O形圈、帽形滑环，如图1所示。模型参数选用车氏密封TB6-IIB100×5.7型孔用帽形滑环式组合密封。材料参数上，丁腈橡胶O形橡胶圈采用Mooney-Rivlin模型，其参数见3.2节；帽形滑环采用增强PTFE，弹性模量为1 GPa，泊松比为0.3[13]；活塞杆与缸体均采用42CrMo，取弹性模量为214 GPa，泊松比为0.29。

对模型进行网格划分，均采用四节点双向性轴对称四边形单元CAX4R，划分结果如图2所示。通过网格无关性验证，当划分网格数量为5 133时，计算结果随网格个数的增加波动小于0.8%，因此在后面的计算中采用该网格数量。整个运动过程中，向有流体压力侧运行为压缩行程，相反方向为伸展行程。

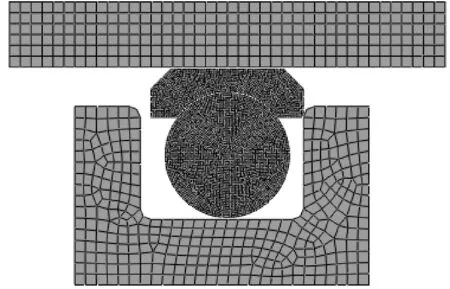
图2 划分网格后的模型

对帽形滑环式组合密静密封性能研究，载荷施加分为两步：(1)对活塞杆施加一定的径向位移实现预压缩；(2)对于帽形滑环式组合密封与流体接触侧施加流体的工作载荷。在动密封性能研究过程中，则需在静密封研究的基础上继续施加活塞杆压缩行程与伸展行程的运动。

3 结果与讨论

3.1 系统参数定义

对于整个系统而言，O形圈与帽形滑环是系统中的易损件，其最大Von Mises应力能反映其是否容易损坏。同时系统中各接触面上的最大接触应力不应小于工作压力，才能有效密封流体。因此需要对O形圈与帽形滑环的最大Von Mises应力，活塞杆、O形圈、帽形滑环、缸体间的最大接触应力进行研究，各参数定义如表1所示。

表1 帽形滑环式密封关键参数

3.2 静密封性能研究

在静密封的研究过程中，主要探究不同密封间隙和工作压力对帽形滑环式密封关键参数的影响。

3.2.1 工作压力、密封间隙对Von Mises应力的影响

随着工作压力和密封间隙的不同，O形圈和帽形滑环的最大Von Mises应力σo和σc的变化如图3和图4所示。

图3 O形圈的最大Von Mises应力与工作压力、密封间隙 的关系

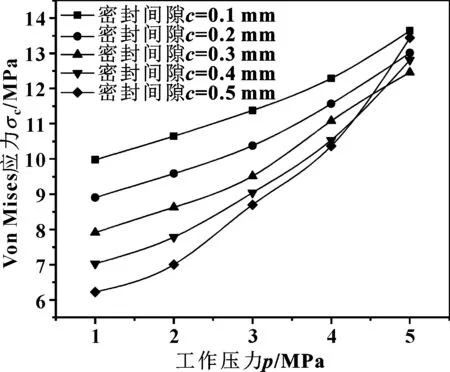
图4 帽形滑环的最大Von Mises应力与工作压力、密封间隙 的关系

由图3可知：随着工作压力的升高，由于O形圈受到流体的压力进一步压缩，因此在相同间隙下σo逐渐升高；在较低压力时，密封间隙对于σo的影响较为显著；随着工作压力的升高，不同密封间隙下的σo差距逐渐缩小，这是由于随着压力升高，压缩较小的O形圈与流体的接触面积较大，而压缩较大的O形圈与流体接触面积较小，因此σo在一定范围内趋于一致。

由图4可知：随着工作压力的升高，在相同间隙下σc逐渐升高；当密封间隙较小时，σc上升速率较密封间隙较大时增大，这是由于在间隙较大时，O形圈的刚度较小，流体压力作用于帽形滑环时绕O形圈的“翘曲运动”较为明显，因此会在外侧尖点形成较大的应力。

3.2.2 工作压力、密封间隙对接触应力的影响

随着工作压力和密封间隙的不同，活塞杆与O形圈间、O形圈和帽形滑环间、帽形滑环与缸体间的最大接触应力的变化如图5—7所示。由图5—7可以得到，随着工作压力的增加与密封间隙的减小，各接触面上的接触应力均呈上升趋势。

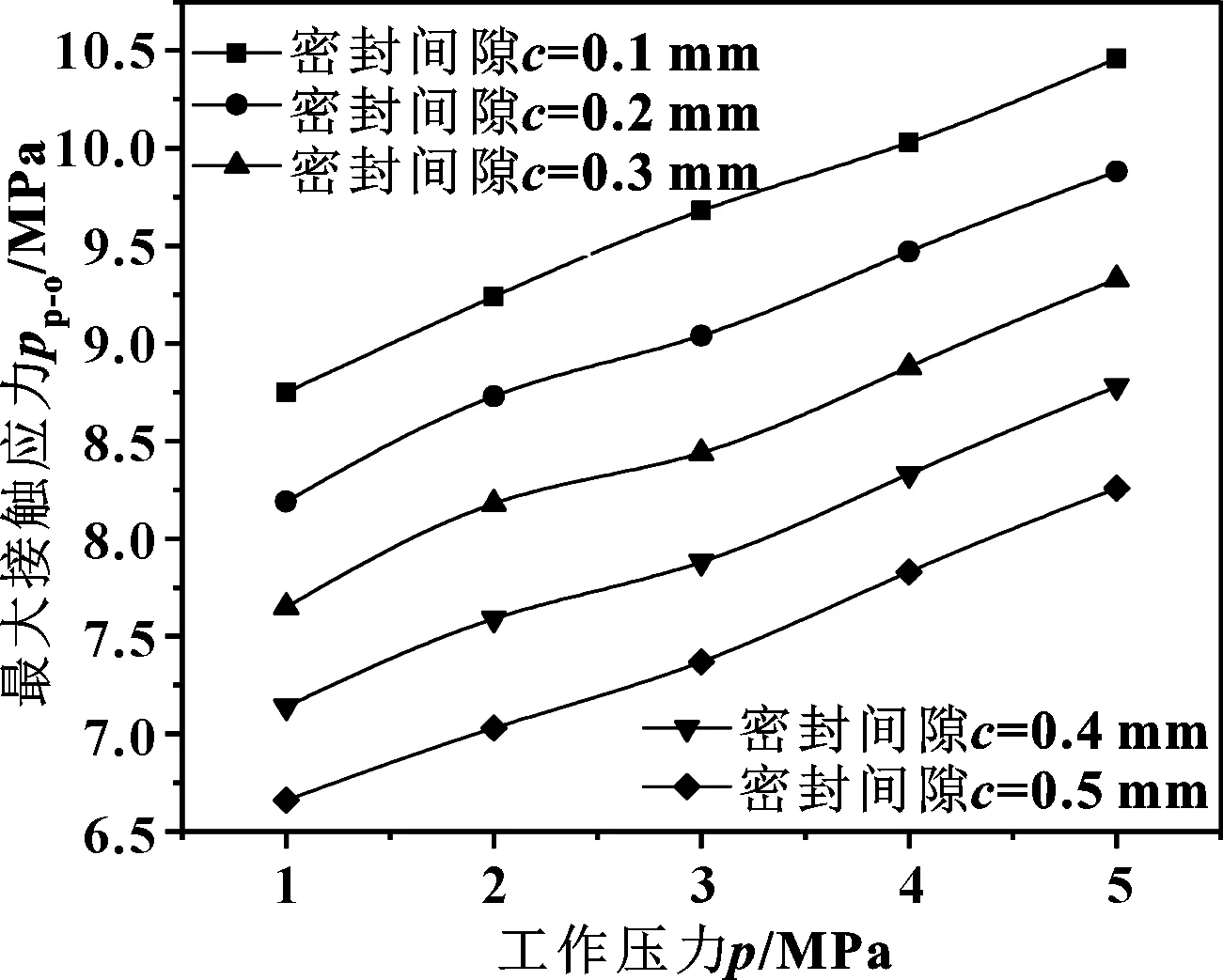
图5 活塞杆和O形圈间的最大接触应力与工作压力、密封 间隙的关系

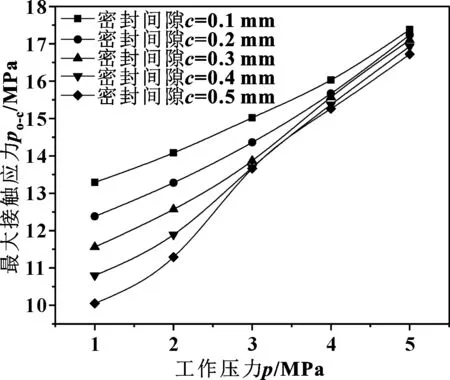
图6 O形圈与帽形滑环间的最大接触应力与工作压力、密封 间隙的关系

图7 帽形滑环与缸体间的最大接触应力与工作压力、密封 间隙的关系

如图5所示，在相同工作压力下随着密封间隙的增长活塞杆与O形圈间的最大接触应力pp-o呈线性增长的趋势；随着工作压力的升高，不同间隙下pp-o的增长幅度相同。如图6所示，在较低的工作压力下，密封间隙对于O形圈与帽形滑环间的最大接触应力po-c的影响较为显著；随着工作压力的升高，大密封间隙下的po-c增长幅度先增加后逐渐与其他间隙下的po-c增长幅度基本一致。如图7所示，帽形滑环与缸体间的最大接触应力pc-c的变化趋势与活塞杆与O形圈间的最大接触应力pp-o的变化规律基本相同。

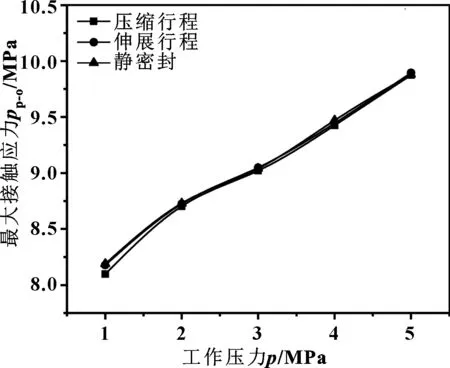
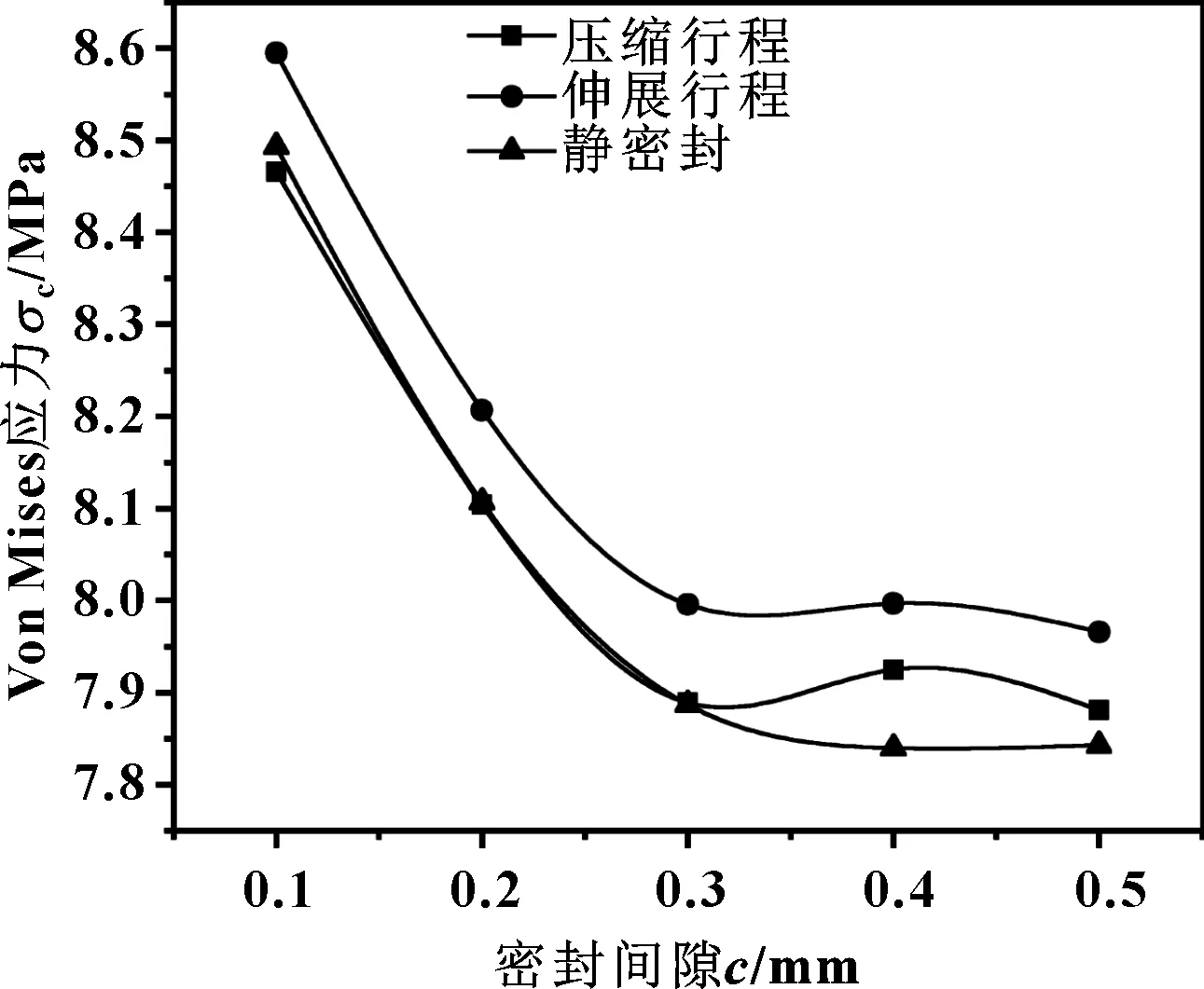
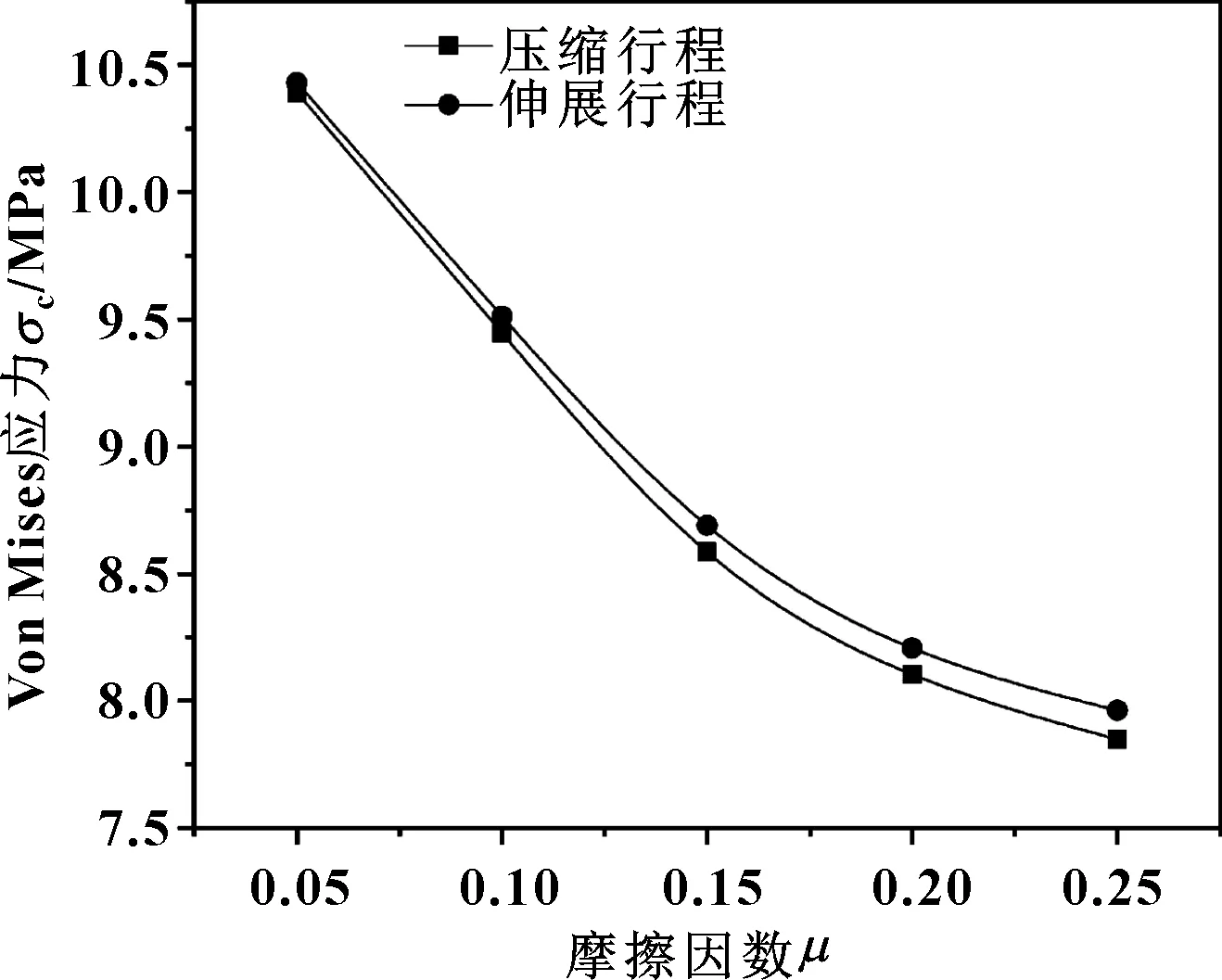
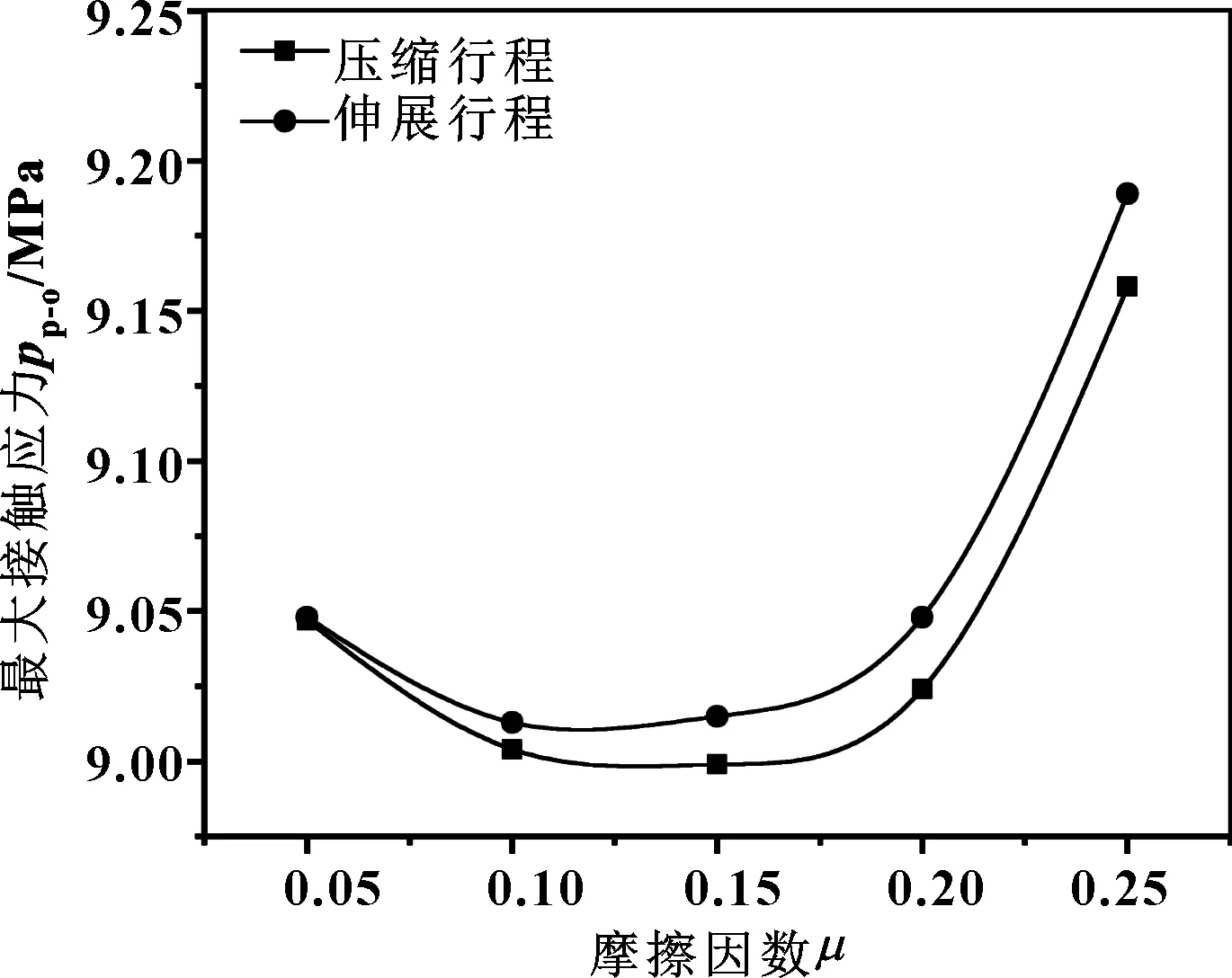
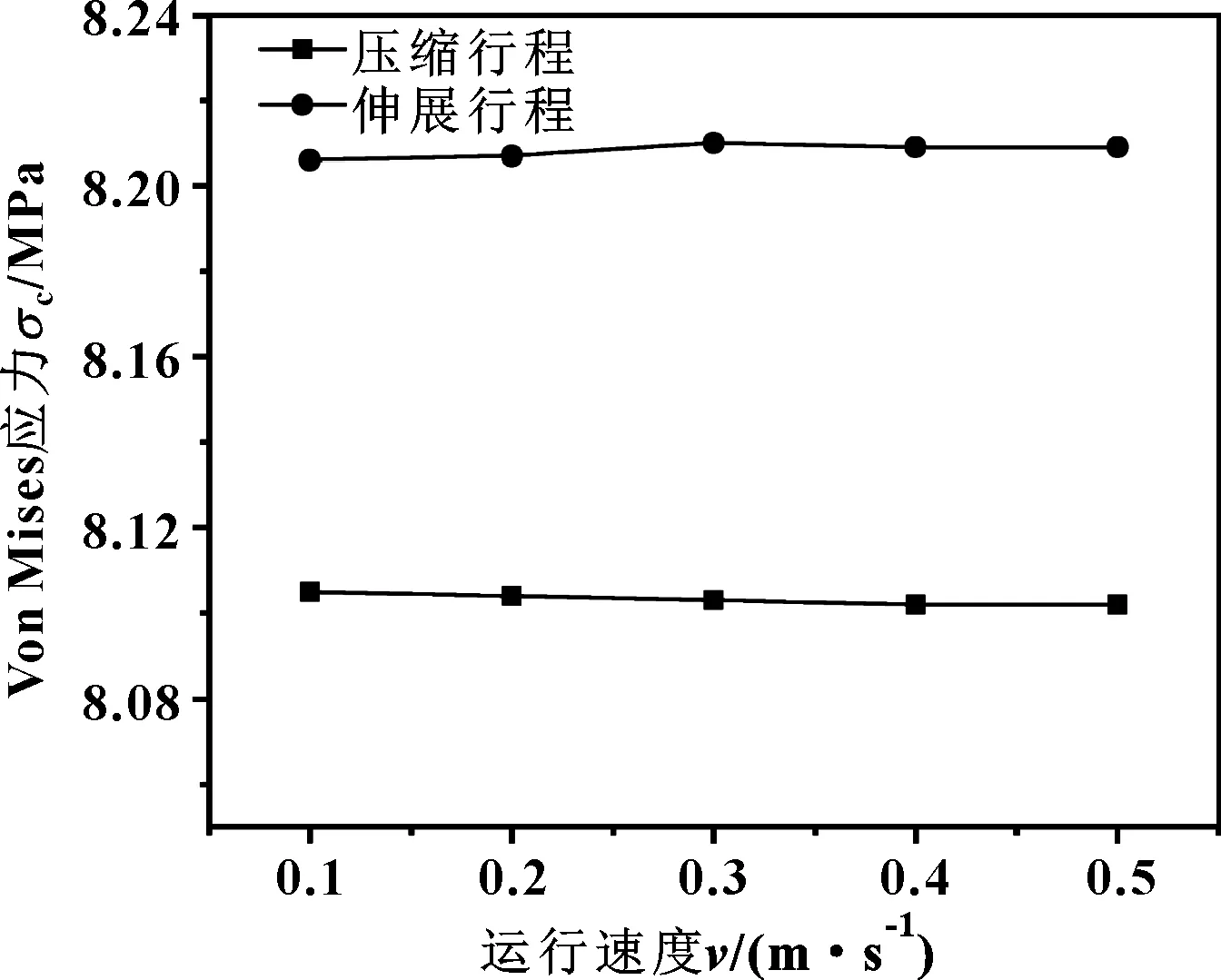
综合分析图5—7可以得到，在同一状态下pp-o

3.3 动密封性能研究

在实际使用中，O形圈容易损坏，同时通过前面分析可知，活塞杆与O形圈间的最大接触应力是影响密封可靠性的关键。因此，在动密封研究中，着重对O形圈的最大Von Mises应力σo以及活塞杆与O形圈间的最大接触应力pp-o进行研究，探究在不同工作压力、密封间隙、摩擦因数和运动速度下帽形滑环式组合密封的密封性能。

3.3.1 工作压力对密封性能的影响

设定摩擦因数为0.2，密封间隙为0.2 mm，活塞杆运行速度为0.2 m/s，在不同工作压力(p=1～5 MPa)下压缩行程、伸展行程与静密封条件下的O形圈最大应力σo、活塞杆与O形圈间的最大接触应力pp-o的变化如图8、9所示。

图8 O形圈最大应力与工作压力的关系(μ=0.2,c=0.2 mm,v=0.2 m/s)

图9 活塞杆与O形圈间的最大接触应力与工作压力的关系 (μ=0.2,c=0.2 mm,v=0.2 m/s)

由图8可看出：随着工作压力的增大伸展行程的σo逐渐增大且与静密封过程中的σo变化不大；在压缩行程中，系统工作压力较低时，系统的摩擦力大于工作压力，活塞杆带动密封件在密封槽内窜动，导致O形圈具有转动的趋势，形成较大应力；当工作压力逐渐加大，系统的摩擦力小于工作压力，密封件不发生移动。因此在压缩行程中σo先减小后逐渐增大。在实际使用中，应注意对应实际工况选择合适的密封间隙，在保证密封的情况下防止密封件出现窜动。

从图9可以得到：对于相同的工作压力，在静密封、压缩行程、伸展行程中的活塞杆与O形圈间的最大接触应力pp-o差别不大，随着工作压力的升高，pp-o呈线性增长。

3.3.2 密封间隙对密封性能的影响

设定摩擦因数为0.2，工作压力为3 MPa，活塞杆运行速度为0.2 m/s，在不同密封间隙(c=0.1～0.5 mm)下O形圈最大应力σo、活塞杆与O形圈间的最大接触应力pp-o的变化如图10、11所示。

图10 O形圈最大应力与密封间隙的关系(μ=0.2,p=3 MPa,v=0.2 m/s)

图11 活塞杆与O形圈间的最大接触应力与密封间隙的 关系(μ=0.2,p=3 MPa,v=0.2 m/s)

由图10可得：在不同间隙下压缩行程、伸展行程与静密封下的σo差别不大；随着密封间隙的增大σo逐渐减小，并且随着密封间隙的增大σo减小的幅度逐渐变小。由图11可知：在相同间隙下压缩行程、伸展行程与静密封下的pp-o基本一致，且随着密封间隙的增加pp-o呈线性下降。

结合图8—11可知，该密封的密封间隙为0.3 mm时既能保证系统有效密封，同时也能保证系统的应力较小，这与车恒德密封手册中推荐的该密封的密封间隙范围为0.3～0.4 mm吻合。

3.3.3 摩擦因数对密封性能的影响

设定密封间隙为0.2 mm，工作压力为3 MPa，活塞杆运行速度为0.2 m/s，在不同摩擦因数(μ=0.05～0.25)件下压缩行程、伸展行程与静密封条件下的O形圈最大应力σo、活塞杆与O形圈间的最大接触应力pp-o的变化如图12、13所示。

图12 O形圈最大应力随摩擦因数的变化(c=0.2 mm,p=3 MPa,v=0.2 m/s)

图13 活塞杆与O形圈间的最大接触应力随密封摩擦因数 的变化(c=0.2 mm,p=3 MPa,v=0.2 m/s)

如图12所示，随着摩擦因数的增大，压缩行程和伸展行程的σo均逐渐减小；同时随着摩擦因数增大两行程的σo差距逐渐加大且压缩行程σo略小于伸展行程。如图13所示，随着摩擦因数的增大pp-o先略微减小后逐渐增大，但pp-o整体变化幅度不大。因此加大系统的摩擦因数能够在一定程度上降低O形圈的最大应力并提高相同条件下的接触应力，但是也应在设计过程考虑由于摩擦因数的增加带来的磨损加剧对于密封的影响。

3.3.4 运行速度对密封性能的影响

设定摩擦因数为0.2，密封间隙为0.2 mm，工作压力为3 MPa，在不同运行速度(v=0.1～0.5 m/s)下压缩行程、伸展行程与静密封条件下的O形圈最大应力σo、活塞杆与O形圈间的最大接触应力pp-o的变化如图14、15所示。

图14 O形圈最大应力随往复运动速度的变化(μ=0.2,c=0.2 mm,p=3 MPa)

图15 活塞杆与O形圈间的最大接触应力随往复运动 速度的变化(μ=0.2,c=0.2 mm,p=3 MPa)

如图14所示，不同速度下，压缩行程的σo略小于伸展行程，随着速度的增加σo变化不显著。如图15所示，压缩行程的和伸展行程的pp-o差距不大，但伸展行程的pp-o逐渐减小，压缩行程的pp-o逐渐增大，但其压缩行程的pp-o增长速率较慢。

总体来看，速度对于密封性能的σo和pp-o的影响有限，但速度的增加会导致摩擦的加剧，影响密封寿命。特别是在高速往复系统中应考虑摩擦产生的热量堆积现象对密封的影响。

4 结论

(1)静密封条件下，活塞杆与O形圈间的最大接触应力小于O形圈与帽形滑环间的最大接触应力，O形圈和帽形滑环间的最大接触应力小于缸体与帽形滑环间的最大接触应力，即活塞杆与O形圈间的最大接触应力是决定密封性能的关键因素；随着工作压力的增大、密封间隙的减小，O形圈和帽形滑环最大Von Mises 应力，活塞杆与O形圈间、O形圈与帽形滑环间、缸体与帽形滑环间的最大接触应力均逐渐增大。该密封在研究的参数下均能达到良好的密封效果。

(2)随着工作压力的增大，伸展行程的O形圈最大Von Mises 应力逐渐增大且与静密封过程中的最大Von Mises 应力变化不大；在研究的参数下，由于O形圈在较低工作下发生窜动，压缩行程中O形圈最大Von Mises 应力先减小后增大，因此在设计过程中应充分考虑低压工作过程中密封件窜动对于密封可靠性的影响。

(3)压缩行程或伸展行程下的O形圈最大Von Mises 应力随着密封间隙的增大逐渐减小；压缩行程或伸展行程下活塞杆与O形圈间的最大接触应力随着密封间隙的增加线性下降。在密封间隙为0.3 mm时较为合适，这与车氏密封手册推荐值0.3～0.4 mm吻合。

(4)随着摩擦因数的增大，压缩行程和伸展行程的O形圈最大Von Mises 应力均逐渐减小，活塞杆与O形圈间的最大接触应力先略微减小后逐渐增大。系统摩擦因数的增大能够在一定程度上降低O形圈的最大应力并提高相同条件下的接触应力，但设计过程中也因考虑由于摩擦因数的增加带来磨损加剧对密封的影响。

(5)随着速度的增加，O形圈最大Von Mises 应力和活塞杆与O形圈间的最大接触应力变化不显著，但速度的增加会导致摩擦的加剧，特别是在高速往复系统中应考虑摩擦产生的热量堆积现象对密封的影响。