混凝土的损伤模型的比较研究

谷钰



混凝土的损伤模型的比较研究

谷钰

（安徽理工大学 土木建筑学院，安徽 淮南 232001）

混凝土的准脆性力学行为可用连续损伤力学理论进行描述。比较研究了几种损伤本构模型类型，介绍了几种损伤加载面和损伤变量的表达式，分析了利用正则化解决网格依赖性的几种典型方法。

损伤模型；损伤变量；当量应变；损伤加载面

混凝土是由水泥砂浆和骨料组成的非均质复合材料，包含大量的初始微裂纹，特别是在粗骨料和砂浆之间的界面，在加载过程中微裂纹的进一步扩展导致了在低应力水平下混凝土的非线性行为。这种由细观结构缺陷产生、扩展等不可逆变化引起的材料力学性能的劣化即为损伤。

混凝土的上述损伤机制可用损伤本构模型较好地加以描述。损伤模型是在热力学框架下构建，在材料的损伤状态下定义一个合适的损伤变量，用损伤变量建立的本构和演化方程来描述受损材料的力学行为。在热力学框架下，各向同性线弹性未损伤材料在损伤状态下的本构关系为：

=（1－）0∶. （1）

式（1）中：为二阶应力张量；为标量损伤变量，[0，1]；0为无损混凝土的四阶弹性刚度张量；为二阶应变张量。根据基本未知量的类型，损伤模型可分为应力驱动型（以应力为基本未知量）和应变驱动型（以应变为基本未知量），具体如下。

1 应力驱动的损伤模型

Manzoli[1]建立了一种应力驱动的损伤模型，在应力空间中指定损伤加载面为：

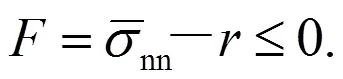
函数（）定义了软化方程：

（）=0exp[（1－/0）]. （3）

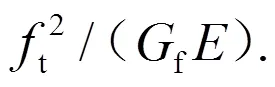
此时，损伤演化方程可以由内部变量定义∈：

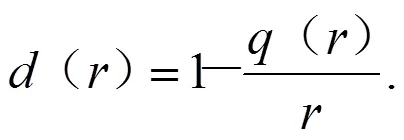
但是这种由应力驱动的损伤模型存在局限性，因为其难以区分应变软化和因卸载引起的应力路径。

2 应变驱动损伤模型

准脆性材料微裂纹的扩展主要是由拉伸应变引起的，这意味着可在应变空间中定义损伤加载面：

（eq，）=eq－≤0. （5）

式（5）中：eq为控制损伤演化的当量应变；为损伤阈值。

本节重点介绍几种广泛使用的应变驱动的损伤模型。

2.1 Mazars模型

Mazars[2]建议的当量应变的表达式为：

eq=‖+‖. （6）

式（6）中：i为主应变，<>+=（+||）/2.

由于拉伸和压缩时，混凝土表现的力学行为不同，因此可分别定义拉、压损伤变量：

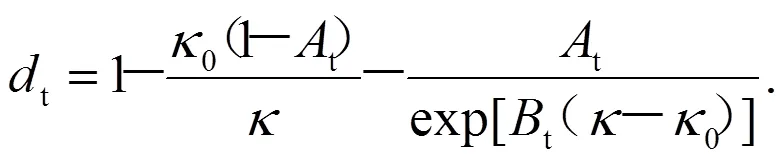
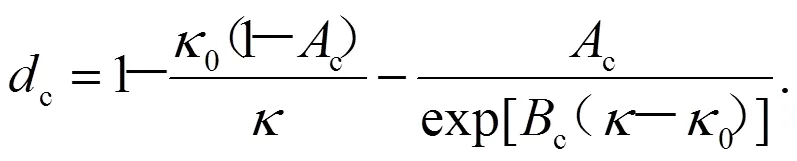
式（7）（8）中：0为初始损伤阈值；t，t，c，c是材料的特征参数，可以通过单轴压缩试验和弯曲试验获得。

2.2 Pegon模型

Pegon[3]对Mazars的当量应变进行了修正：

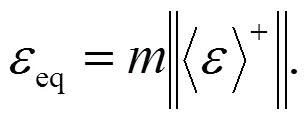
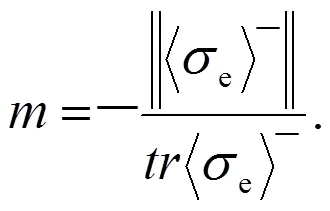
式（9）（10）中：<>﹣=（－||）/2.

损伤变量单调不能减小，可表示为：

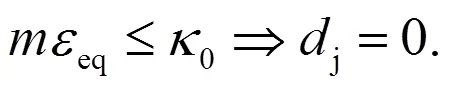
式（11）（12）中：=，，分别为压缩和拉伸。

2.3 Oliver模型

Oliver[4]提出了适用于双轴应力状态下的当量应变：

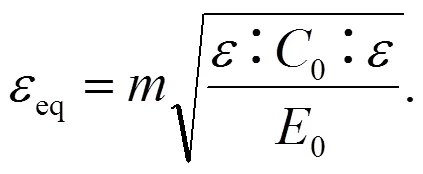
是依据应力e的加权因子，定义为：

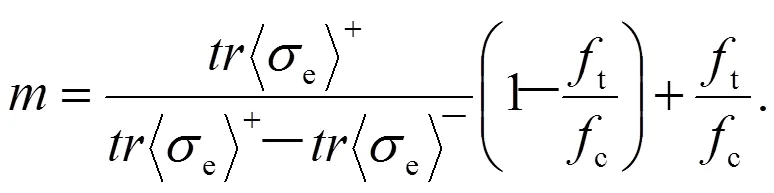
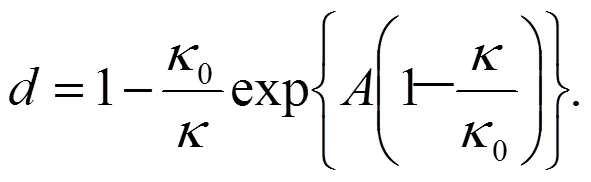
式（14）（15）中：0＜0≤.

参数依据断裂能f和有限单元特征长度确定，定义为：

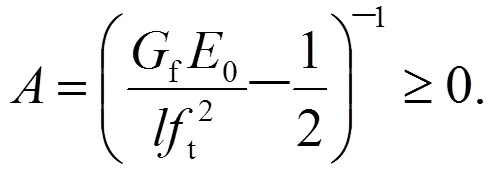
2.4 de Vree模型

de Vree[5]模型由改进Von Mises当量应变而得到：

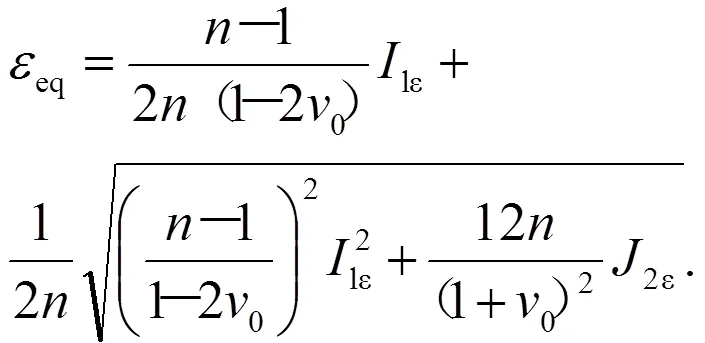
式（17）中：为拉伸与压缩强度的比值；1ε和2ε为应变不变量。

损伤变量定义为：

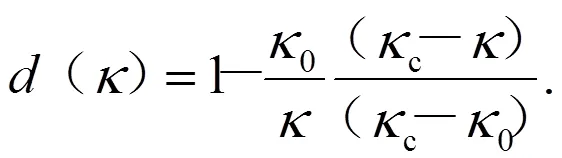
式（18）中：c为损伤阈值临界值。

2.5 Wei He模型

何伟[8]提出了考虑应变状态的不对称性引入两个局部当量应变来量化材料的局部变形状态，分别为压缩当量应变

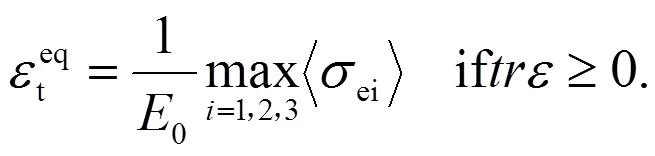
式（19）（20）中：1σ和2σ为有效应力不变量；和为由混凝土试验确定的材料常数。

和可以定义为：

最终定义损伤演化规律：

3 网格依赖性问题的正则化

在对损伤本构模型进行数值计算时，为了避免网格依赖性问题，常采用正则化方法进行修正，本节对此予以介绍。

3.1 断裂带正则化方法

Bazant[6]提出了一种断裂带模型的方法。该方法的基本思想是将应变软化模量定义为断裂能和网格尺寸的函数。该方法容易实现编码，应用简单。但这种正则化的缺点是显而易见的，虽然这种方法可以描述全局变形，但局部状态的预测仍然存在网格依赖性，甚至可能出现不切实际的结果。

3.2 非局部损伤理论

解决应变和损伤局部化的最合理方案之一是非局部损伤理论。在这种方法中[7]，一点上的非弹性应变或损伤的演变不仅由相关点处的状态变量控制，而且还由它们的相邻场控制，并定义一个非局部损伤变量：

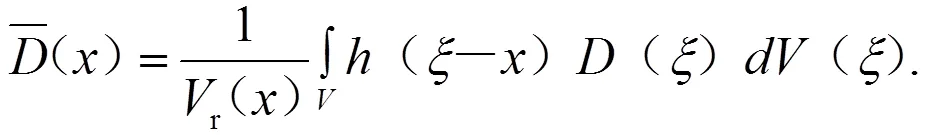
式（25）（26）中：为空间域；（－）为非局部加权函数，它随距离|－|单调减小。

非局部损伤理论是一种正则化软化材料应变局部化的有效方法，也是局部断裂分析方法中最重要的数值程序。

4 结论

应力驱动的损伤模型无法区分应变软化和因卸载引起的应力变化；应变驱动的损伤模型不能准确描述在双轴加载情况下的力学行为；对损伤本构模型进行数值计算时，可以通过断裂带正则化和非局部损伤理论来克服网格依赖性。

［1］Manzoli O L，Maedo M A，Bitencourt Jr L A G，et al.On the use of finite elements with a high aspect ratio for modeling cracks in quasi-brittle materials［J］.Engineering Fracture Mechanics，2016（153）：151-170.

［2］Mazars J.A description of micro-and macroscale damage of concrete structures［J］.Engineering Fracture Mechanics，1986，25（5-6）：729-737.

［3］Pegon P，Anthoine A.Numerical strategies for solving continuum damage problems with softening： application to the homogenization of masonry［J］.Computers & structures，1997，64（1-4）：623-642.

［4］Oliver J，Cervera M，Oller S，et al.Isotropic damage models and smeared crack analysis of concrete［C］//Proc.SCI-C Computer Aided Analysis and Design of Concrete Structures. 1990.

［5］De Vree J H P，Brekelmans W A M，Van Gils M A J.Comparison of nonlocal approaches in continuum damage mechanics［J］.Computers and Structures，1995（55）：581-581.

［6］Bažant Z P，Oh B H.Crack band theory for fracture of concrete［J］.Matériaux et construction，1983，16（03）：155-177.

［7］Bažant Z P，Pijaudier-Cabot G.Nonlocal continuum damage，localization instability and convergence［J］. Journal of applied mechanics，1988，55（02）：287-293.

［8］He W，Wu Y F，Xu Y，et al.A thermodynamically consistent nonlocal damage model for concrete materials with unilateral effects［J］.Computer Methods in Applied Mechanics and Engineering，2015（297）：371-391.

2095－6835（2019）05－0017－03

TU352.11

A

10.15913/j.cnki.kjycx.2019.05.017

谷钰（1993—），女，硕士研究生，研究方向为混凝土结构的计算模型。

〔编辑：张思楠〕