坍塌作用下埋地管道数值分析

娄彦鹏

大庆油田有限责任公司天然气分公司规划设计研究所

公路、铁路、航运、海运和管道运输是石油天然气主要运输方式。其中，管道运输最安全、经济，对环境破坏最小。由于管道的诸多优点，随着石油和天然气需求量和产量的增加，管道的铺设也迅猛发展。但近年来，随地质灾害频发，埋地管道的意外事故时有发生。地质灾害轻则使管道部分露出地面，影响管线运输安全；重则造成管道整体位移、悬空，导致局部变形、应力集中；最为严重的是造成管道断裂、油气泄漏，甚至发生爆炸，造成人员伤亡、财产损失、资源浪费，影响人民生活和工业生产[1-4]。

土层坍塌是一种典型的地质破坏形式，对埋地管道破坏非常巨大，可能会产生较大纵向、横向变形，造成管道断裂，对管线的正常运行构成威胁[5-12]。因此，本文在众多研究的基础上，利用ADINA有限元软件，建立土体坍塌下埋地管道的三维实体模型，研究土层坍塌段长度、宽度、管道壁厚等对管道竖向最大位移、轴向最大应变和最大有效应力的影响。

1 计算模型的建立

为了简化计算模型，本文主要考虑外界地质灾害对管道的影响，因此，在计算时忽略内压影响。文中管道为输油管道，建立及计算模型时将油品质量转化为均布荷载施加在管道上。

采用三维实体模型模拟坍塌作用下埋地管道，坍塌段与两侧土体之间有一定的间隔，坍塌段不考虑管土相互作用，使坍塌段土层瞬时发生坍塌，即在短时内使其作用在管道上，运用ADINA有限元软件建立坍塌作用下埋地管道三维实体模型，根据VonMises准则来判断管道材料是否进入屈服阶段。

管道材料为API 5L X60进口钢材，管道屈服极限为414 MPa，应力应变关系采用输油气钢质管道抗震设计规范中的三折线简化模型（图1），材料参数见表1。土体应力应变关系为摩尔库伦模型，土的弹性模量为3.5×104MPa，土的密度为2000kg/m3，泊松比为0.30，膨胀角为0，内摩擦角为45°，黏聚力为10 MPa。土体坍塌段长度取10、20、30、40 m，采用八节点单元分别对土体及管道进行网格划分。通过ADINA有限元软件的自动划分网格功能进行单元划分，管轴方向为0.5 m一个单元，管道圆周方向划分为16个单元，两侧土体为1 m一个单元，坍塌段土体为0.5 m一个单元，坍塌作用下的埋地管道有限元模型如图2所示。

图1 应力应变关系三折线模型Fig.1 Three line model of stress-strain relationship

坍塌段与两侧土体之间有一定间隔。在进行计算时，仅考虑土体及管道的自身重力。坍塌段土层不设置任何约束，管道两端不设置任何约束，两侧土体底面为固定约束。

图2 坍塌作用下埋地管道有限元模型Fig.2 Finite element model of buried pipe under collapse

2 数值模拟结果分析

2.1 静力分析与动力分析

坍塌土体自重作用下的埋地管道，管径D=0.508 m，壁厚t=0.015 9 m，管道埋深h=1.7 m，管道长度l1=223.5 m，坍塌段长度l2=20 m，两侧非坍塌土体长度l3=100 m，坍塌段宽度d1=4 m，两侧土体宽度d2=5 m，分别采用静力分析方法和动力分析方法模拟坍塌作用下的埋地管道。

静力分析方法和动力分析方法模拟坍塌作用下埋地管道竖向位移云图分别如图3、图4所示，坍塌作用下埋地管道竖向最大位移、轴向最大应变及最大应力如表2所示。最大位移、应变、应力、差异率分别用 ymax、εmax、σmax、 δ表示（以下类同）。

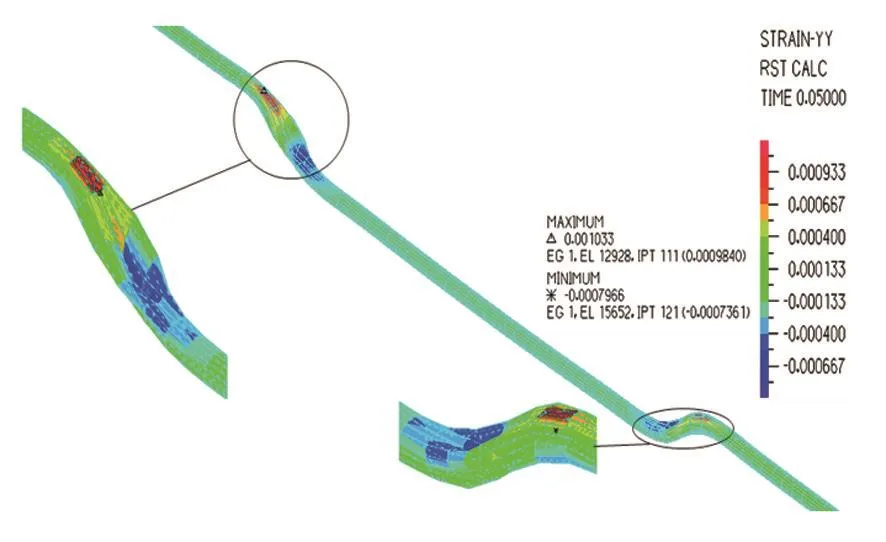
图3 静力分析管道应变云图Fig.3 Static analysis of strain cloud chart

通过应变云图发现最大拉压应变发生在两侧土体与坍塌段断开处。

通过表2中竖向最大位移、轴向最大应变及最大应力发现，相同情况下，动力分析的竖向最大位移要比静力分析的大17.5%（差异率δ），动力分析的最大应变要比静力分析的大15.1%，动力分析的最大应力要比静力分析的大19.9%。坍塌具有突发、随机的特点，故应该采用动力分析方法进行分析。

表1 材料参数Tab.1 Material parameters

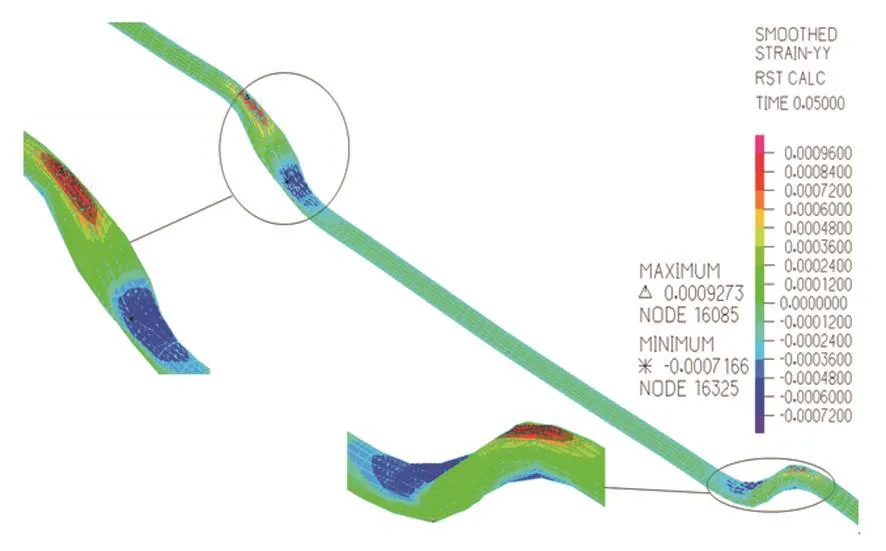
图4 动力分析管道应变云图Fig.4 Dynamic analysis of strain chart

表2 静力方法和动力方法分析最大位移、应变及应力Tab.2 Maximum displacement，strain and stress of static and dynamic methods

2.2 不同管道壁厚数值模拟

采用动力分析方法，建立并分析坍塌作用下埋地管道模型，管料为进口钢材API 5L X60，管径D=0.762 m，壁厚t=0.023 8 m，管道埋深h=1.7 m，管土摩擦系数μ=0.4，管道长度为l1=223.5 m，坍塌段长度l2=20 m，两侧非坍塌土体长度为l3=100 m，坍塌段宽度d1=4 m，两侧土体宽度d2=5 m，分别模拟了管道壁厚t为0.015 9、0.023 8、0.031 8 m时的坍塌作用下埋地管道。

通过应变云图发现最大拉压应变发生在两侧土体与坍塌段断开处。

坍塌作用下埋地管道竖向最大位移、轴向最大应变及最大应力如表3所示。δ1表示管道厚度为0.015 9 m和0.023 8 m时的各模拟值相应差异率，δ2表示坍塌段宽度为0.023 8 m和0.031 8 m时各模拟值相应的差异率（表4）。

表3 不同壁厚管道最大位移、应变及应力Tab.3 Maximum displacement，strain and stress with different wall thickness

表4 不同壁厚管道位移、应变及应力的差异率Tab.5 Difference ratio of displacement，strain and stress with different wall thickness %

通过表3中竖向最大位移、轴向最大应变及最大应力发现，在坍塌作用下，壁厚为0.015 9 m时，最大位移、轴向最大应变及最大应力为最大；壁厚为0.023 8 m时次之，壁厚为0.031 8 m时最小。

2.3 不同坍塌段宽度数值模拟

采用动力分析，建立并分析坍塌作用下埋地管道模型，土体类型为黄土，管道材料为进口钢材API 5L X60，管径D=0.762 m，壁厚t=0.023 8 m，管道埋深h=1.7 m，管土摩擦系数 μ=0.4，两侧非坍塌土体长度为l3=100 m，管道长度为l1=223.5 m，坍塌段长度l2=20 m，两侧土体宽度d2=5 m，分别模拟了坍塌段宽度d为1、2、3、4 m时的坍塌作用下埋地管道。不同坍塌段宽度示意图如图5所示。

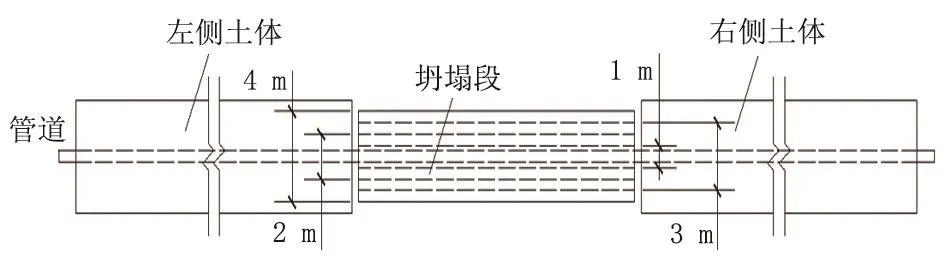
图5 不同坍塌段宽度示意图Fig.5 Collapse schematic diagram with different width

通过应变云图发现最大拉压应变发生在两侧土体与坍塌段断开处。

坍塌作用下埋地管道竖向最大位移、轴向最大应变及最大应力如表5所示。δ1表示坍塌段宽度为1 m和2 m时各模拟值相应的差异率，δ2表示坍塌段宽度为2 m和3 m时各模拟值相应的差异率，δ3表示坍塌段宽度为3 m和4 m时各模拟值相应的差异率（表6）。

表5 不同坍塌段宽度最大位移、应变及应力Tab.4 Maximum displacement，strain and stress with different width of collapse

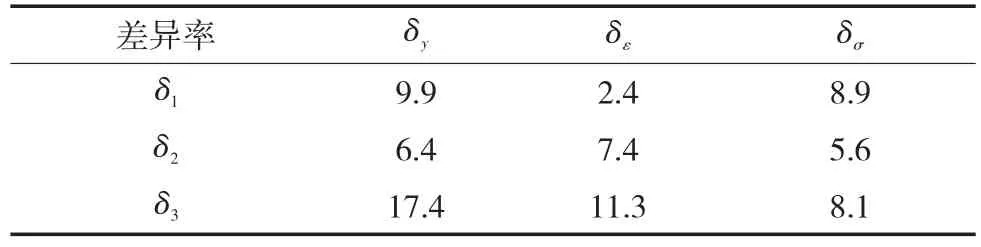
表6 不同坍塌段宽度位移、应变及应力的差异率Tab.7 Difference ratio of displacement，strain and stress with different width of collapse %

通过表5中竖向最大位移、轴向最大应变及最大应力发现，在坍塌作用下，当坍塌长度一定时，随着坍塌宽度的增加，竖向最大位移、轴向最大应变及最大应力都逐渐增加。

2.4 不同坍塌段长度数值模拟

建立并分析坍塌作用下埋地管道模型，管道材料为进口钢材API 5L X60，管径D=0.762 m，壁厚t=0.023 8 m，管道埋深h=1.7 m，管土摩擦系数μ=0.4，管道长度l1=223.5 m，坍塌段宽度d1=4 m，两侧土体宽度d1=5 m，两侧非坍塌土体长度为l3=100 m，分别模拟了坍塌段长度l2为10、20、30、40 m时的坍塌作用下埋地管道。

不同坍塌长度、坍塌作用下埋地管道竖向位移云图分别如图6～图9所示。其竖向最大位移、轴向最大应变及最大应力如表7所示。δ1表示坍塌段长度为10 m和20 m时各模拟值相应的差异率、δ2表示坍塌段长度为20 m和30 m时各模拟值相应的差异率、δ3表示坍塌段长度为30 m和40 m时各模拟值相应的差异率（表8）。

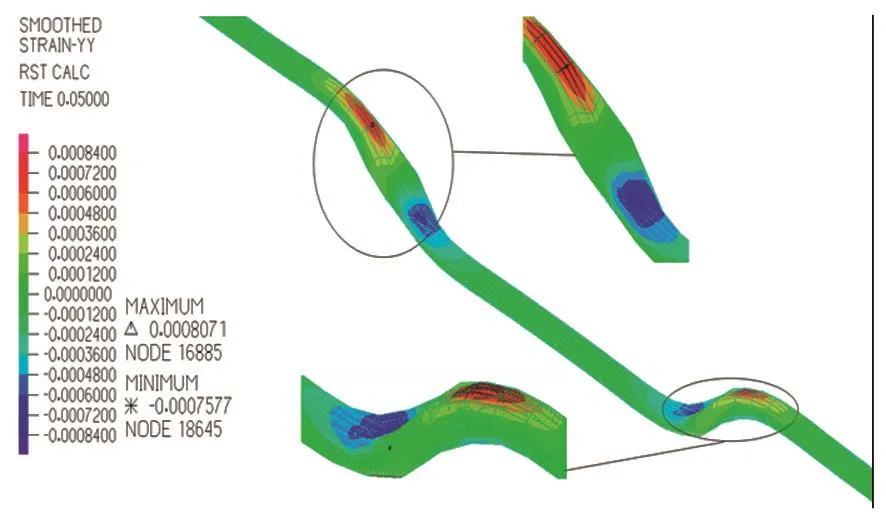
图6 坍塌段长度为10 m时管道应变云图Fig.6 Strain cloud chart of pipe when the length is 10 m

图7 坍塌段长度为20 m时管道应变云图Fig.7 Strain cloud chart of pipe when the length is 20 m

图8 坍塌段长度为30 m时管道应变云图Fig.8 Strain cloud chart of pipe when the length is 30 m

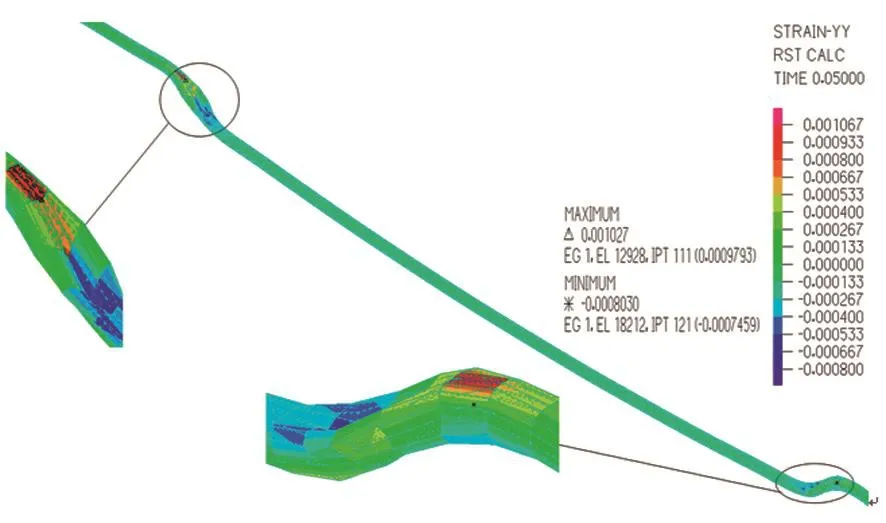
图9 坍塌段长度为40 m时管道应变云图Fig.9 Strain cloud chart of pipe when the length is 40 m

表7 不同坍塌段长度最大位移、应变及应力Tab.5 Maximum tensile stres，displacement with different length of collapse

表8 不同坍塌段长度位移、应变及应力的差异率Tab.9 Difference ratio of displacement，strain and stress with length of collapse %

通过应变云图发现最大拉压应变发生在两侧土体与坍塌段断开处。

通过表7中最大拉应力和竖向最大位移值发现，在坍塌作用下，随着坍塌段长度的增长，竖向最大位移、轴向最大应变及最大应力越来越大；并不是所有的坍塌长度、管道的应力都超过屈服应力，说明了不同工况下管道的失效长度不同。进行工程设计时，应根据不同的地质条件及工况来重新判定该情况下管道所能允许土体的坍塌长度。

3 结论

通过对坍塌作用下埋地管道进行有限元模拟表明，当坍塌段土体宽度变化时，宽度为4 m时的位移、应变、应力要比宽度为1 m时的位移、应变、应力大37.3%、22.5%、24.2%；当管道的坍塌长度变化时，坍塌段长度为40 m时的位移、应变、应力要比长度为10 m时的位移、应变、应力大44.1%、21.3%、56.7%；坍塌段宽度越宽，长度越长，管道的位移、应变及应力越大，可能遭受到的破坏越大；管道的薄弱位置为土层断开处。因此，在进行设计时，如果管线需要经过易坍塌地质区域，要根据不同工况重新评估管道所能够承受的土体坍塌长度；选择管壁较厚的管道，同时勘察该地区土体可能发生坍塌的长度及宽度，加强薄弱位置的防护措施。该研究对坍塌作用下埋地管道工程设计具有一定的指导意义。