在轨可修复单机可靠性分析方法

李 杰，杨 宏，乔军卿，赵国清

（1.山东航天电子技术研究所，烟台 264003；2.中国空间技术研究院载人航天总体部，北京 100094）

引 言

以往空间任务中，当电子设备如数管计算机、远置单元、热控管理单元等在轨发生故障时，受技术水平限制，是无法派送人员和装备到现场进行修复的。国内传统单机设备研制阶段，在进行可靠性评估时，一般不考虑修复因素对单机和系统可靠性影响，一般通过软硬件资源的冗余容错设计，来提高设备和系统的可靠性，确保空间任务的完成[1-3]，如采用双机冷备[4]、双机热备[5]、三模冗余容错[6]、多机复合容错[7]等措施。这就不可避免地导致了设备和系统设计复杂度、体积及重量的增加[8]。

对于载人空间任务而言，任务期间有人值守，能够对单机设备进行一定程度的在轨维修和维护[9]。在通用化程度较高的前提下，可以大幅减少备件数量、减轻整器重量，降低航天器研发成本。随着航天电子故障诊断技术及健康预测与管理技术的不断发展，包括深空探测在内的无人飞行器的电子设备与系统的远程维护与在轨自主保障修复也具有了可行性[10]。具有在轨可修复能力可大大提高软硬件资源的利用效率，提高设备与系统可靠性。

地面可修复系统已有一些研究成果，如Rao等[11]结合马可夫过程及系统动态仿真研究了一个含备份的可修复系统，Moghaddass 等[12]根据维修人员及工作的串并组合对系统可用度进行了分析，孔德良等[13]将系统分解为若干小模块，先分别计算再综合为系统可用度。而在航天领域，单机在轨可修复是近年来才面对的一个新课题，目前的研究也主要集中在修复方法上[14-15]，对可修复单机的可靠性问题鲜有研究。如不加区别地直接使用非可修复单机可靠性分析方法，就不能准确把握在轨可修复单机的可靠性特点，分析结果也难以对研制工作起到指导作用。因此，有必要开展在轨可修复单机可靠性分析方法研究。

1 单机可靠性模型

1.1 相关概念

1）可靠度（Reliability）与可用度（Availability）

在可靠性分析理论中[16]，可靠性是指产品在规定的条件下和规定时间内，完成规定功能的能力。可靠性的概率度量叫可靠度，它是指在规定时间段内设备无故障运行的概率。可用度是在某种维修条件下、在规定时间内维持系统正常功能的概率。可用度又分为2类：①系统在某一时刻处于正常状态的概率，称为瞬态可用度；②当时间趋于无穷时，系统瞬态可用度的极限，称为稳态可用度。

可用度是可修复单机的一个重要的可靠性指标。对可修复单机，任务末期可用度趋于一个稳定值，可用稳态可用度来衡量。可靠度适合作为非可修复设备的可靠性指标，也可引申为可修复单机在修复率为0时的可用度。本文采用可用度作为可修复单机和非可修复单机可靠性比较的基准。

2）修复过程

修复是指当一个设备或一个系统发生故障时，通过技术手段使之重新恢复到能够行使正常功能状态的过程[17]。

本文假设修复后单机完好如初。修复可采用多种方法，既可以是对故障部件进行软硬件维修，也可以是更换故障部组件。完整的单机修复过程一般包括以下几个步骤：①检测到故障发生，诊断故障原因，隔离故障位置，确定单机修复方案（如：软件在线更新，冷热复位、断电更换硬件等）；②通过软件在线更新、复位、断电更换硬件等，恢复单机正常功能，包括为更新或更换而进行的拆除、取备件、替换等各项工作，以及更新或更换后的软硬件测试及校准；③再次加入系统，行使正常功能。

本文所涉及的单机修复，既可以是维修单机的软件、硬件或部组件，也可以是整机更换。在备件充足的情况下，修复工作可多次重复进行。一般修复过程都含有拆除、测试校准、再接入等步骤。但一些特殊情况，如在线软件更新，就不一定需要单机拆除和接入操作。

3）修复率

修复率μ按单机平均修复时间的倒数计[18]，μ=平均修复时间越短，修复率越高。此处的修复时间涵盖了从检测到故障发生，到消除故障、系统恢复正常功能的时刻为止，包括了故障检测、诊断与隔离的时间t1，软硬件获取、维修及测试校准时间t2，以及再次加入系统的时间t3，即：MTTR=t1+t2+t3。

假设单机通用化程度高，软硬件一致性较好，所采用的故障检测、诊断与隔离算法是一样的，则t1可视为是不变的。忽略单机位置给替换操作带来的差异，t3也可视为是不变的。随着故障类型及备件储备情况的不同，t2则会发生比较大的变化，尤其是受到备件补充能力的影响。在MTTR中，t2所占比例较大，一般情况下远超t1和t3。本文主要以t2来估计MTTR及μ。

1.2 可靠性模型

假设单机工作寿命分布与修复时间分布是相互独立的，经过修复的故障单机其工作寿命分布如新的单机一样。单机失效率λ不随时间变化而变化，且单机可靠度R（t）呈指数分布，即R（t）=e-λt。

单机状态S共有2 种状态：正常状态和故障状态，即

非可修复单机可靠性模型如图1所示，表示单机在t时刻，有λdt的概率从正常状态转移到故障状态。当转移到故障状态（S=1）后，由于没有修复，只能停留在故障状态（S=1），单机失效。

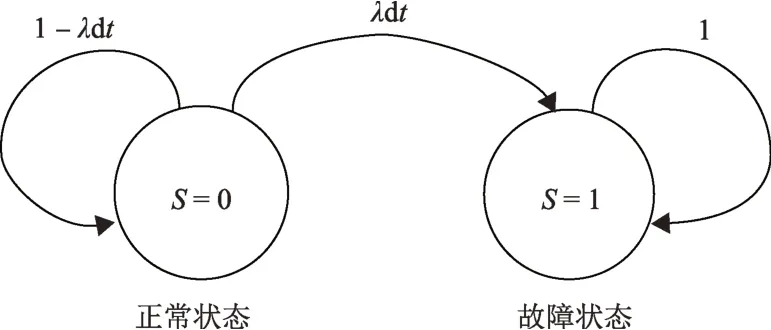
图1 非可修复单机可靠性模型Fig.1 Reliability model of none-repairable single-unit

可修复单机可靠性模型如图2所示。由于具有修复能力，故障单机有一定的概率μdt从故障状态中恢复到正常状态。

图2 可修复单机可靠性模型Fig.2 Reliability model of repairable single-unit

1.3 可修复单机可用度估计公式推导

假设初始加电后，单机处于正常工作状态。对图2的可修复单机可靠性模型建立状态方程为

其中：Pi（t）为t 时刻S=i（i=0,1）状态下单机正常工作概率。

整理式（1），得

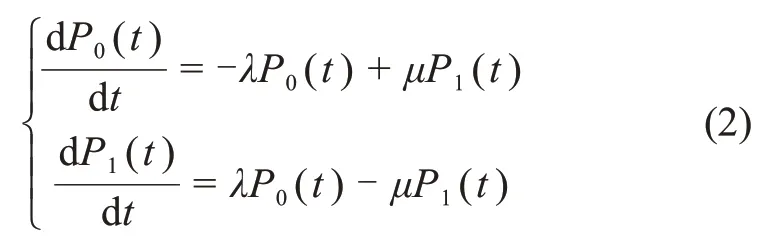
对式（2）使用Laplace变换，得到

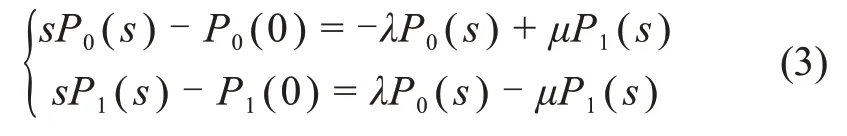
根据前文假设，单机初始处于正常状态，故P0（0）=1，P1（0）=0。代入式（3），并解方程可得

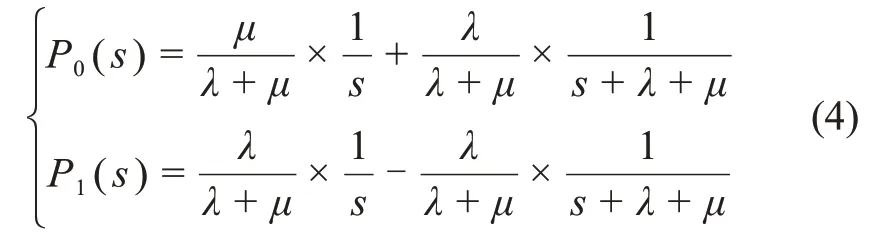
对式（4）使用Laplace反变换，可得

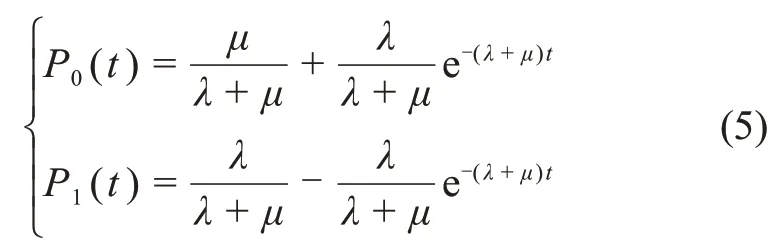
其中：P0（t）为t时刻单机处于正常工作状态的概率；P1（t）为t时刻单机处于故障状态的概率。

根据可修复单机可用度的定义，在t时刻单机正常工作状态的概率即为单机瞬态可用度为

根据式（6），在确定任务周期、单机的失效率，以及不同备件状态下的修复率后，就可以得到可修复单机在整个任务周期的可用度变化趋势。

对于非可修复单机，可视其修复率μ=0，代入式（6），可得：A(t) = e-λt=R(t)，即对非可修复单机，其可靠度与可用度是等效的。

2 可修复单机可用度分析

本文以某信息系统通用计算机作为在轨可修复单机进行可用度仿真分析。

2.1 参数设置

设任务周期为15年（共131 400 h），假定单机失效率λ=10-4/h。根据表1所列维修类型和备件储备状态估算不同情况下的修复率。

表1 不同维修类型和备件状态下的修复率估计Table1 Repair rate estimation for different maintaining and backup states

表1中，第1～3项在线软件更新是在轨维修项目之一，但这3 项不涉及故障的检测、诊断与隔离过程，也没有设备的拆除和再接入过程，更新软件是地面经过检验和测试后上传至飞行器，因此其平均修复时间是按照从系统注入单机，并经过在轨测试后正式投入使用这段时间。

图3 第1～6项的可用度曲线Fig.3 Availability curves of No.1～6 in table 1

2.2 计算与分析

将上述参数（任务周期、单机失效率、修复率）带入式（6），得到可修复单机在15年任务周期内，不同维修类型和备件状态下的可用度变化曲线。

因表1 中第1～6 项可用度值比较大且分布密集，将第1～6项的可用度曲线用图3表示，其余的可用度用图4表示。表1中的各项在第15年末的可用度值如表2所示。

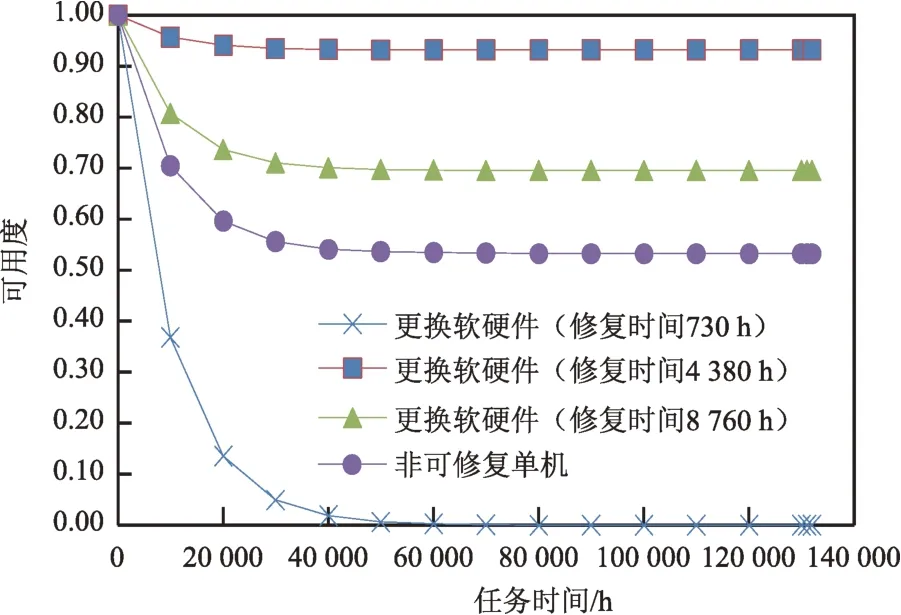
图4 第7～9项及非可修复单机的可用度曲线Fig.4 Availability curves of No.7～no.9 in table 1，and none-repairable single-unit

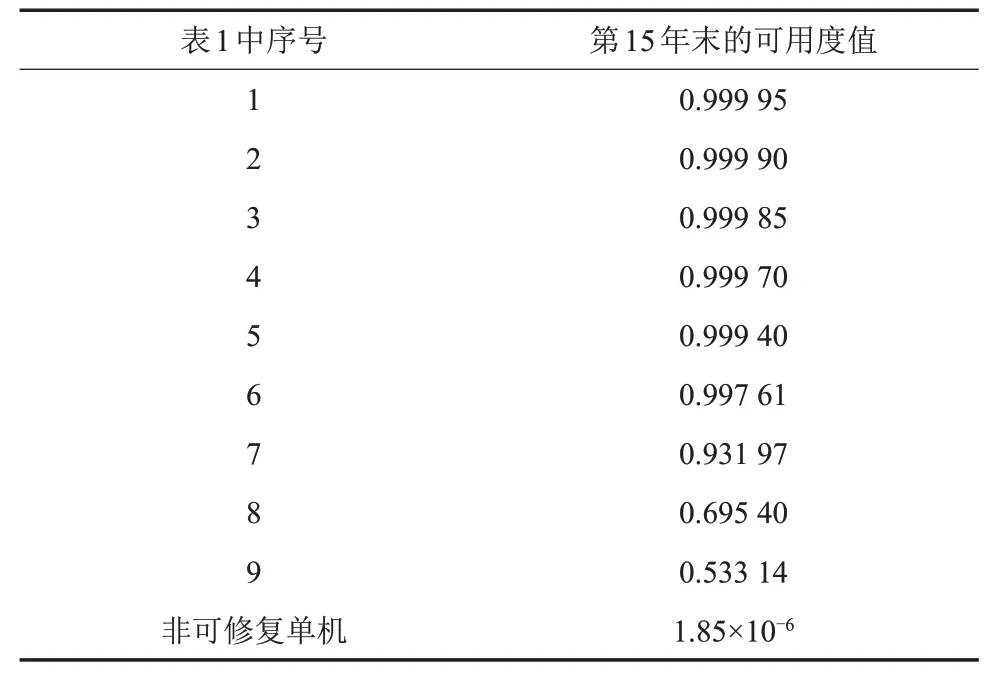
表2 表1中各项及非可修复单机在15年末的可用度值Table2 Table1 availability values at the end of 15-year mission of No.1～no.9 in，and none-repairable single-unit

仿真计算中使用的单机失效率相对较高，非可修复单机在1 000 h可用度就跌至0.905。表1中的第1～7项因具有较高的修复率，在任务周期中始终保持比较高的可用度，在任务末期单机可用度仍高于0.9。表1中的第8、9项因修复率相对较低，任务末期可用度也相对较低，但远高于非可修复单机。这表明，具有可修复能力，同时具有较高的修复率，可以使失效率相对大的单机也能在任务周期内保持较高的可用度，从而使得飞行器具有较高的可靠性。

3 修复率与失效率关系快速估计

当t趋于无穷时，由（6）式可得到单机稳态可用度[19]为

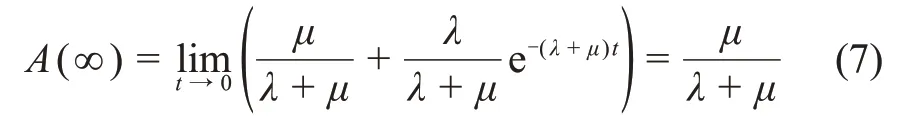
由图3 和图4 可见，随着时间的推移，可用度曲线分别趋近并各自收敛于某一个稳定数值，区别在于不同失效率和修复率下这个数值是不一样的。

当（7）式中修复率μ分别趋于0和∞两个极端值时，得到以下两种极端情况：当μ→0 时，MTTR→∞，A（∞）→0，即在没有修复力的情况下，稳态可用度最终趋于0。当μ→∞时，MTTR→0，A（∞）→1，相当于具有瞬间修复能力，单机在任务周期内几乎全程可用。

按照文献[17]的方法将式（7）作泰勒展开，有

略去高次项后，得到一个近似估计公式（8），可作为设计初期，在期望的稳态可用度下，对单机修复率和失效率的关系进行快速估计。如：当期望任务末期的稳态可用度不低于0.9 时，就需要满足μ≥ 10λ的条件。

此处的关系估计只与μ和λ的比例有关，与它们的绝对数值无关。实际应用中，可根据当前单机失效率水平确定合适的维修策略，以更有效地调动资源；或可根据现有的维修能力预计所需的单机失效率，在备件充足、通用程度高、操作便捷、平均修复时间短的场景下，可适当降低对单机失效率的要求，这有利于系统成本控制。

4 结 论

深空探测任务周期长，要求电子设备具有较高的可靠性。通过采用新的技术和新的设计方法等让设备具有可修复能力，是提高其可靠性的一种有效途径。本文研究了在轨可修复单机的可靠性分析方法，推导了单机瞬态可用度计算公式，给出了修复率和失效率关系快速估计方法。研究结果表明，具有可修复能力对提高单机有效工作时间、提升单机可用度起着非常大的作用，修复时间越短，修复率越高，单机可用度提升幅度就越大，可靠性越高。通过对修复率与失效率关系快速估计，可在设计初期阶段为维修策略和可靠性规划提供决策依据。