基于水动力学模型的灌溉渠道水流量水方法研究
2019-03-21谢崇宝商学营
白 静,谢崇宝,黄 斌,商学营
(1.中国灌溉排水发展中心,北京 100054;2.中国水利水电科学研究院,北京 100044;3.滨州市簸箕李引黄灌溉管理局,山东 滨州 251700)
0 研究背景
农业是中国的用水大户,其中2016年,农业用水量为3 768 亿m3,占用水总量的62.4%[1]。在优化农业用水配置和推行农业节水的过程中,流量的量测是用水管理的重要基础。灌溉渠道的流量是灌区水调度、用水总量管理和水费计收的重要依据[2,3]。实现用水总量控制、定额管理的前提为灌区用水的精确计量。在渠道重要的分水节点、产权交割点、用水户分界点建立有效且实用的量水设施十分必要。
现有的量水方法有:量水槽、量水堰、建筑物量水和标准断面量水法等。在灌区中渠道断面多以梯形或者U型为主,量水槽是灌区明渠量水使用最广泛的设施,且精度较高[4-6]。对于比较复杂的设施,如巴歇尔水槽的施工偏差会降低量水精度[7,8];对于结构简单的设施,如梯形薄壁堰[9]和三角形薄壁堰[10],减小渠道过水面积或者抬高渠底,通常会造成额外的水头损失或者减小渠道的过水面积,对于含沙量较大的明渠水流,容易造成泥沙淤积。建筑物量水方式的使用范围也有一定的局限性,一般应用于建筑物附近的渠段。标准断面量水法需要在渠道上选择水力条件良好的断面,根据大量的水位-流量资料率定得到流量水位关系公式,通过实测水位获得流量。对于非恒定流动,流量水位并不是一一对应关系,而是呈现绳套曲线关系[11-13]。除此以外,当上下游流动条件改变时,流量水位关系公式需要重新率定。在某些极端的条件下,渠道内存水且水流静止时,标准断面量水法失效。均匀流计算公式的使用条件非常严格,在非恒定或者非均匀流的情况下,计算公式会照成一定的误差。
在本文中提出一种两点水位量水法,在渠道上避开水流急变段,沿着渠道选择两个断面,分别安装水位计并测量断面的水位,求解水动力学控制方程,即可得到渠道的流量。两点水位量水法不需要建造量水建筑物或者安装复杂的仪器,因此不会改变渠道原有的断面形态,基本不产生额外的水头损失。
1 一维水动力学数学模型
一维水动力学的控制方程为[14]。
连续方程:
(1)
动量方程:
(2)
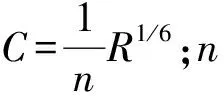
A1jΔQj+B1jΔZj+C1jΔQj+1+D1jΔZj+1=E1j
(3)
A2jΔQj+B2jΔZj+C2jΔQj+1+D2jΔZj+1=E2j
(4)
式中:A1j、B1j、C1j、D1j、E1j、A2j、B2j、C2j、D2j、E2j为离散方程的系数或者常数。当求解断面个数为n时,j=1,2,…,n-1。给定上游断面和下游断面的边界条件时,可以求解出各断面的流量。
2 两点水位量水法
在两点水位量水法中,避开分汊段、汇流段、急变流段和泥沙冲刷淤积段,在渠道上选择2个断面,测量断面的形状在两个测量断面上(断面1-1、断面2-2)安装水位计等水位测量仪器,实时获得断面的水位变化情况,见图1。利用远程传输技术和模块,将断面的水位实时发送到电脑上。将上下游断面的水位数据作为边界条件输入水动力学求解模块,可以求解得到两个断面的流量Q1和Q2,将断面流量的均值作为测量段断面的流量值。
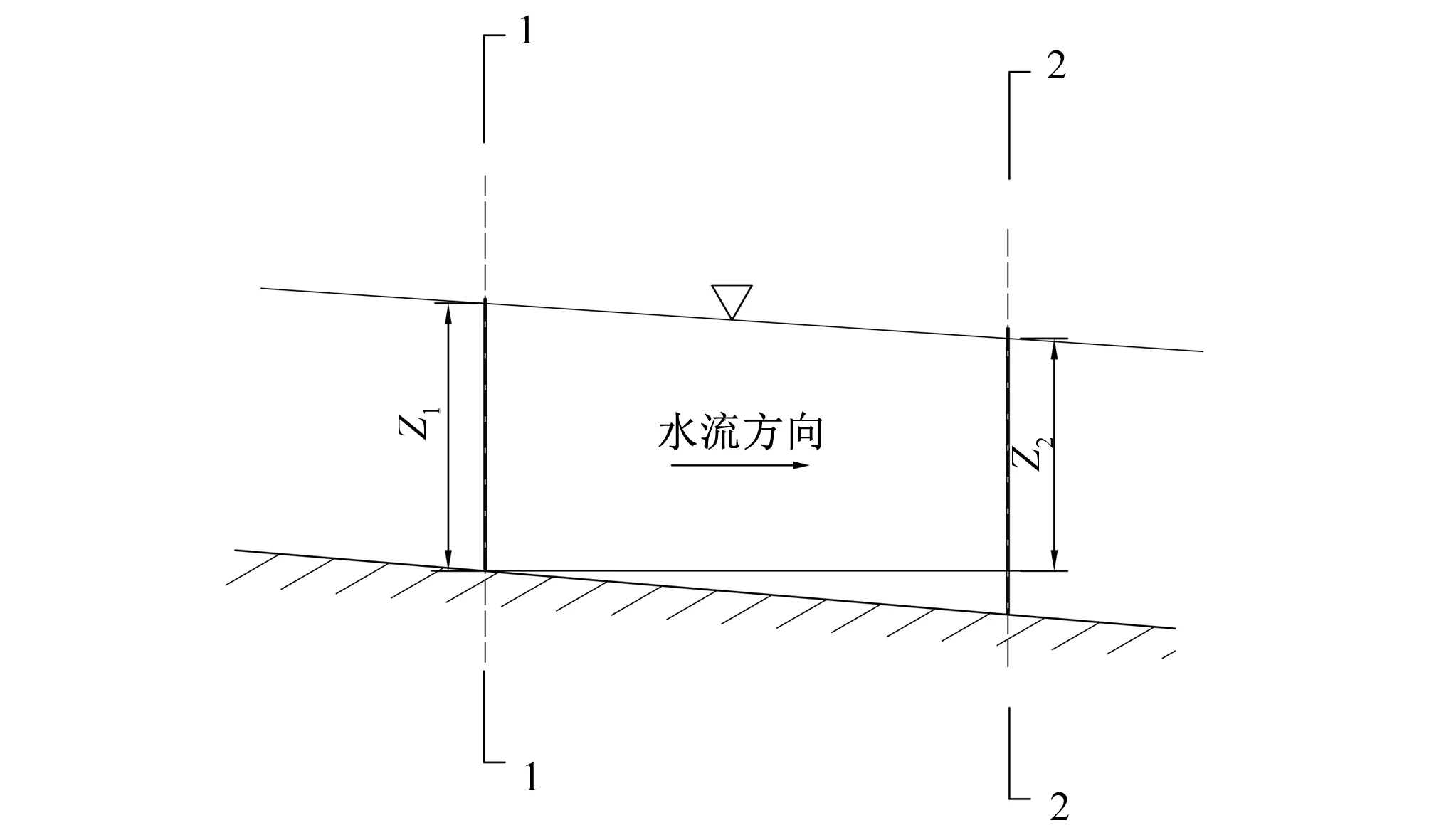
图1 两点水位量水法中水位计布置示意图Fig.1 Schematic diagram of water level indicators in the discharge measurement method by water level at two points
一维水动力学数值求解模型采用Fortran进行编程求解。其边界条件和初始条件设定如下:①物理边界条件即断面形状及断面之间的距离,断面的形状数据以起点据-高程的形式录入、断面之间的距离直接录入;②上下游断面边界数据,在两点水位量水法中采用断面1-1和断面2-2的水位资料作为边界条件。③一维水动力学数值求解模型的初始条件即上下游断面的流量为假定流量,通过迭代计算可以收敛到真实值。
一维水动力学数值求解模型采用已有的水位流量资料并选取合适的四点差分格式的离散系数取θ和时间步长Δt,对断面的曼宁系数n进行率定。在渠道没有水位流量资料的情况下,可以采用流速仪分层分垂线测量多点流速,采用流速面积法测量渠道的流量。断面的流量为:
(5)
式中:vij表示第i个测线上第j个测点的流速;aij表示第i个测线上第j个测点代表的面积。
两点水位量水法对流动的恒定性和均匀性没有要求,可以处理非均匀流和非恒定流动情况。一般情况下,由于断面形状、糙率和底坡沿程发生变化,渠道来流量随着时间发生变化,渠道中建筑物的影响等多种原因,明渠的流动均为非均匀流动。两点水位测量法可以减小流量监测过程中减小因为上下游水流运动条件发生改变造成的系统误差,以及因为忽略水流的非恒定性引起的误差。
3 应用实例研究
由于现有的渠道的流量实测资料不完善,在应用实例研究中,选取水位资料完善的渠段进行流量计算,并与均匀流公式进行比较。A渠段和B渠段均位于簸箕李引黄灌区的干渠上。
(1) A渠段应用实例研究。选用顺直渠段A长1 000 m,渠道横断面为矩形,宽3.97 m,渠道纵坡为1/2 000。渠道断面采用混凝土抹浆处里。在渠段进口断面1-1和出口断面2-2分别安装磁浮子水位计,水位计具有通讯功能,其采集水位的频率为30 min 1次。
渠道曼宁系数n取值为0.013,离散系数θ为0.75,时间步长Δt取为10 s。利用A渠道4月1日22∶00-4月10日6∶00的水位数据和两点水位量水法进行流量的计算,将计算的结果与均匀流公式进行对比,见图2。在图中两点水位量水法计算得到的流量Qt用粗实线表示,利用上游断面1-1的水位数据和均匀流公式计算得到的流量Qe1用虚线表示,采用下游断面2-2的水位数据和均匀流公式计算得到的流量Qe2用细实线表示。流量偏差率e1定义为:
(6)
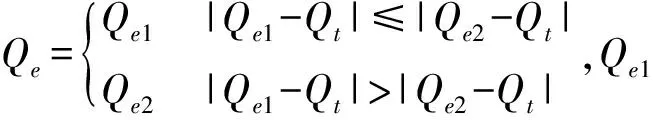
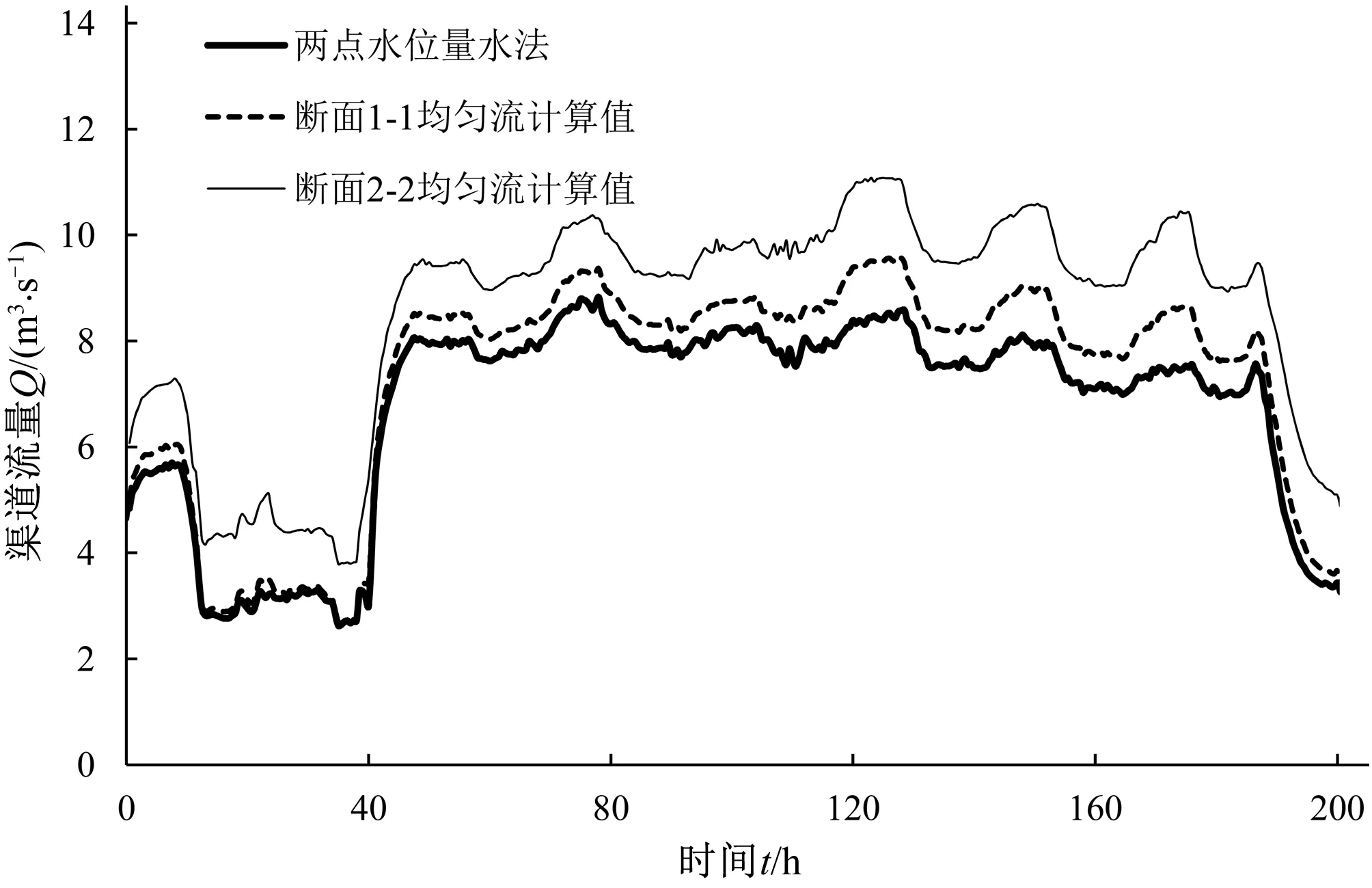
图2 A渠段计算流量对比图Fig.2 Comparisons of computed discharge of Channel A by different ways
对比分析断面1-1和断面2-2的水深过程线(图3)可以发现,该渠段发生了壅水现象,即渠道水面坡度J小于渠道底坡i。采用均匀流公式计算的流量偏大,与采用均匀流公式计算得到的流量相比,偏差率e1介于-0.69%~15.92%之间,其平均值为7.9%。
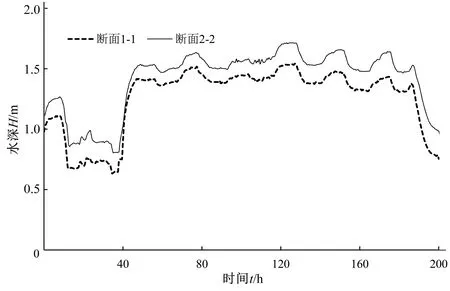
图3 A渠道断面1-1和断面2-2水深Fig.3 Water depth at the cross section 1-1 and cross section 2-2 of channel A
(2) B渠段应用实例研究。选用顺直渠段B进行流量计算,长400.6 m,渠道横断面为矩形,宽14.9 m,高3 m,渠道纵坡为1/800。渠道断面采用混凝土抹浆处里。在断面1-1断面和2-2断面上分别安装水尺,断面1-1和断面2-2之间距离为183.8 m,每日8点、12点和18点人工读取并记录水位。
采用B渠道2018年4月7日8∶00-4月30日18∶00的水位数据和两点水位量水法进行流量过程的计算,计算中采用的参数与A渠道一致。两点水位法计算的流量果与均匀流公式进的对比见图4。图4中,两点水位量水法计算得到的流量Qt用粗实线表示,利用上游断面1-1的水位数据和均匀流公式计算得到的流量Qe1用虚线表示,采用下游断面2-2的水位数据和均匀流公式计算得到的流量Qe2用细实线表示。从图5中可以看出,水面比降J大于渠底坡度i。采用均匀流公式计算得到的流量与两点水位法计算得到的流量之间有偏差,偏差率e1介于-0.08%~19.24%之间,其平均值为4.61%。
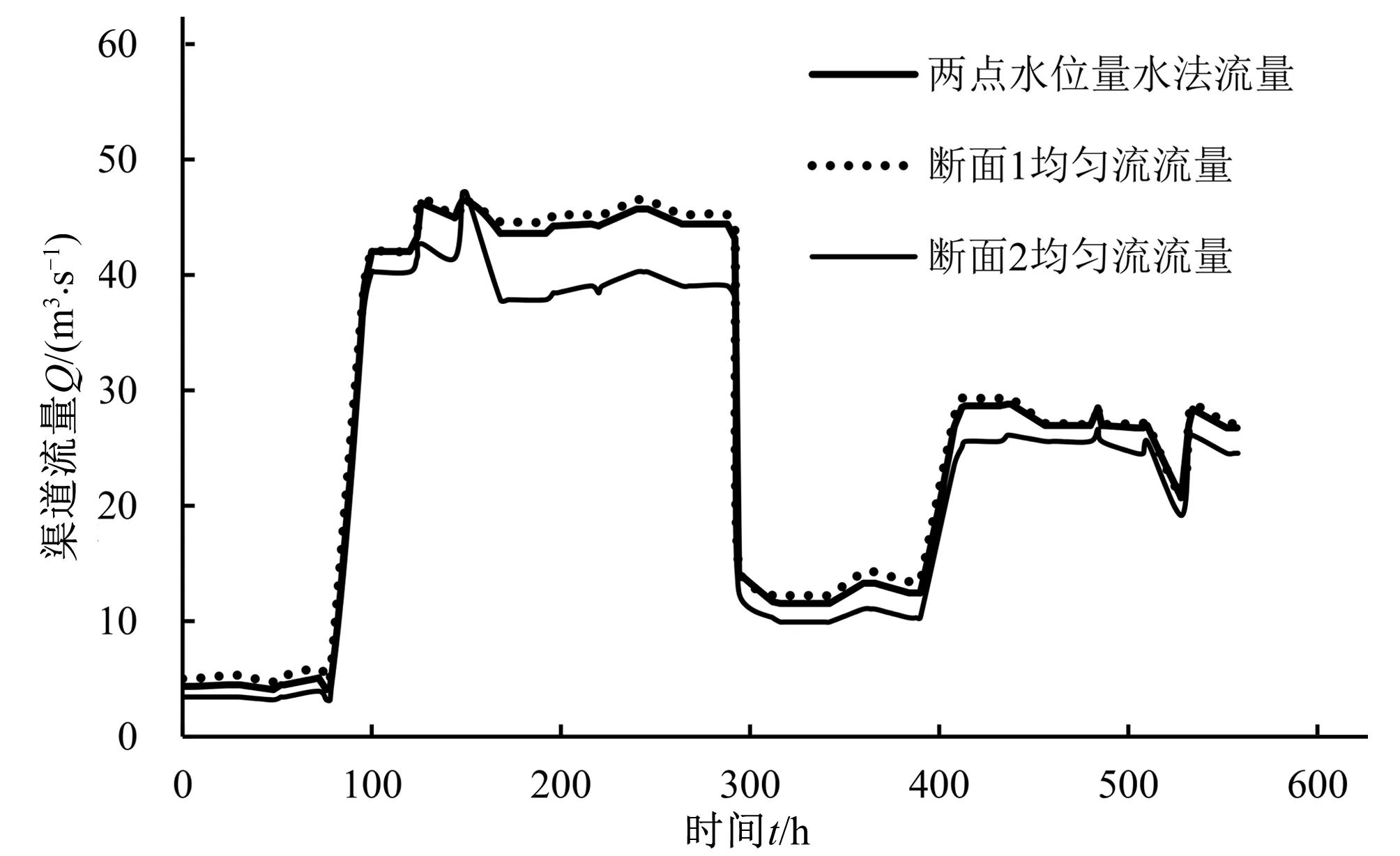
图4 B渠段计算流量对比图Fig.4 Comparisons of computed discharge of Channel B by different ways
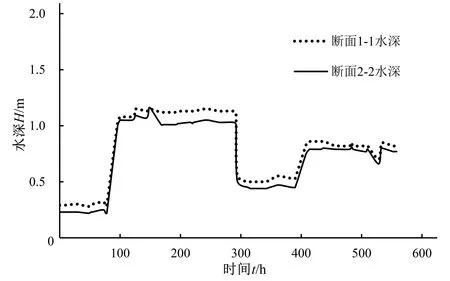
图5 B渠段断面1-1和断面2-2水深Fig.5 Water depth at the cross section 1-1 and cross section 2-2 of channel B
4 研究结论
(1)本文提出了两点水位量水法,在灌溉渠道上沿程选择两个断面,实时测量两个断面的水位变化情况,通过求解水流控制方程得到渠段的流量。两点水位量水法具有明确的物理内涵,流量的计算结果能反映水流的非恒定性和非均匀性。
(2)将两点水位量水法初步用于实际渠道的流量计算,在相同的糙率取值的情况下,两点水位量水法计算的结果比均匀流公式的精度有较大幅度的提高。
□
